三轴磁传感器系统的在线标定*

盛　蔚,蒋　勇

(北京航空航天大学仪器科学与光电工程学院,北京　100191)

三轴磁传感器系统的在线标定*

盛蔚,蒋勇

(北京航空航天大学仪器科学与光电工程学院,北京100191)

摘要:现有的三轴磁传感器的标定方法对于设备的要求过高,系统不能够独立完成标定工作。针对此种情况,提出三轴磁传感器系统的在线标定算法,建立三轴磁传感器系统误差模型,采用椭球曲面拟合三轴磁场数据,利用递推法计算标定参数。达成了传感器系统本身在线独立完成标定的目的,并对在线标定参数的可信度提出了评价方法。通过实验验证了在线标定方法的有效性和在线标定参数可信度评价方法的有效性。

关键词:磁传感器;在线标定;椭球拟合;递推最小二乘法

0引言

三轴磁传感器系统是用来测量地球磁场在载体坐标系下三轴磁场分量大小的传感器系统。既可以与加速度计信息组合起来计算载体姿态[1],又可以当作测量磁场异常的传感器系统用于磁异常定位[2]。根据三轴磁传感器的输出模型,可将外界干扰等效成三轴磁传感器系统三轴磁场数据的零偏误差和标度因数。目前对于三轴磁传感器系统的标定,主要有陈伟等人提出的利用GPS信息作为参考进行标定[3],郭鹏飞等人提出的十二位置不对北标定法[4],以及朱建良等人提出的椭球曲面拟合法[5]。这些方法都有各自的缺点,极大的限制了三轴磁传感器系统在野外的使用,同时也增加了三轴磁传感器系统的使用成本。文中提出的三轴磁传感器系统在线标定算法,继承了椭球曲面拟合标定法的灵活性以及无需转台就能进行等优点,并针对椭球曲面拟合算法无法独立完成计算的缺点,提出了使用递推算法计算标定过程中需要用到的椭球系数的方法。使三轴磁传感器系统能够独立完成标定工作,降低了使用成本,也使其使用范围更加广泛。

1误差模型

地磁场的干扰主要来源于周围环境中的磁性材料产生的磁场。在地磁场和磁性材料产生的干扰磁场共同作用下,三轴磁传感器在载体坐标系下的输出模型[6]可表示为:

(1)

由地磁场的特性,可以认为在一个小区域内,地磁场的强度值为固定值。在理想条件下,三轴磁传感器系统可以测得地磁场在载体坐标系下的三轴磁场分量的值。以三轴磁场强度分量为坐标的测量点将构成一个以地磁场强度为半径、球心在原点的球面。在数学上的表示为:

(2)

上述情况是在地磁场未受到外界环境中磁场干扰的理想条件下才能实现的。事实上,由于存在硬磁干扰和软磁干扰,再加上三轴磁传感器系统轴向间存在的非正交性和磁阻传感器本身存在的零偏误差,上述球面将畸变成一个椭球面。通过旋转三轴磁传感器系统,获取足够多的椭球面上的点,就可以通过拟合算法计算出椭球面方程的系数参数。利用这些系数参数计算出k和u0,对磁场测量值进行补偿,消除三轴磁传感器系统受到的干扰。

2标定参数的计算

将式(2)展开,可得到如下二次标准型方程:

(3)

椭球曲面方程的一般表达式可用下式表示:

(4)

将椭球曲面方程整理为矢量型式:

(5)

对比式(3)和式(5)可得:

(6)

由上式可知,只要知道了椭球曲面方程中的9个系数参数就能够计算出标定参数的值,然后通过标定参数对磁场测量值进行补偿。椭球曲面的拟合方法有牛顿迭代法等,这些方法的共同缺点就是需要存储大量的数据进行计算,需要其他设备协助完成标定参数的计算,限制了其在嵌入式系统中的应用。为此文中提出了一种在线标定三轴磁传感器系统的方法——利用递推最小二乘法对椭球曲面方程进行拟合计算。解决了三轴磁传感器系统标定必须依赖其他设备的缺点

3拟合椭球曲面方程参数的计算

在采用递推最小二乘法计算拟合椭球曲面参数的过程中,有可能会出现系数全为0的奇点[7],而且受到干扰的磁场测量数据还有可能造成拟合椭球曲面发散为双曲面。因此需要对递推过程施加约束条件。不等式形式的约束条件会使参数的计算变得极为困难。为此,Fitzgibbon提出在二维条件下约束不等式[8]可写为4ac-b2=1。Nikos Grammalidis等人将其原理推广到三维条件下[9],即椭球曲面拟合的约束条件为:

在不考虑约束条件的情况下,将前文的椭球曲面方程看作是参数待定的二次曲面方程,若测得N组测量数据,则可写出N个方程,写成矩阵形式为:

(7)

将上式简写为:tN=φNθ。

根据递推最小二乘估计理论的一般公式,θ的递推最小二乘估计公式如下:

(8)

式(8)为不考虑约束条件下的递推公式。对于带线性约束条件的递推最小二乘法,只需要在不带约束的最小二乘法的基础上加上一个修正项即可。

(9)

式(8)在加上约束条件下的补偿公式为式(9),即为约束条件下椭球曲面参数计算的递推公式。将采集到的每组数据代入到递推计算公式中进行计算,直到最后一组数据递推计算完毕,此时θ的最小二乘估计值即为求得的椭球曲面方程的系数参数值。由椭球曲面参数系数即可求得三轴磁传感器系统的标定参数。

4标定质量的评价

对三轴磁传感器系统的标定过程实际上是为了确定上述椭球方程的10个系数参数。椭球参数的计算是基于地磁场强度为固定值的条件,而在标定过程中也无法分辨磁场的来源是地磁场还是其他物体产生的磁场。因此,在三轴磁传感器系统标定时需要一个相对稳定的磁场环境。若外界存在变化的磁场,标定的精度将受到严重的影响,标定计算得到的标定参数也会失效。为了判断标定结果的可信程度,选取递推计算过程中磁场总强度的计算值的平方mTm作为判断标定过程中磁场环境是否稳定参考变量。在稳定的磁场环境中,mTm是一个逐渐收敛的值。递推得到的参数越接近最终结果,mTm的值也会越稳定,最终趋向于一个稳定的值。如果在标定过程中受到变化的磁场的干扰,mTm的值将不能收敛,这就在一定程度上判断出标定结果的可信程度。

在三轴磁传感器系统的标定过程中,每次递推计算后都能得到一组拟合椭球曲面的参数,继而可以计算出标定参数k和u0。由式(2)可得此时磁场强度的计算值,写成三轴分量形式为:

(10)

由磁场的三轴分量计算出磁场强度的平方mTm。在标定结束时,取mTm的最后100个计算值求其方差V。

5实验分析

用于实验的三轴磁传感器系统采用Honeywell磁阻传感器,具有较高的磁场分辨率和稳定的磁场输出。将三轴磁传感器系统安装到六面体工装上,任意旋转变换三轴磁传感器系统姿态。保证采集到的磁场数据在拟合椭球曲面的每个方向上都有分布。旋转工装的速度要缓慢,让每个位置都能采集到足够的数据,如果某个方向的数据过少,很可能会影响到标定的精度。记录采集到3 000组数据并绘图。

在未受到干扰的条件下,采集到的磁场三轴分量测量值数据绘图如图1所示。

图1　无干扰条件下三轴磁场数据情况

在标定过程中采集到的每组数据作为新息进行递推计算。在未受到干扰的条件下,递推计算过程中的磁场总强度平方的计算值绘图如图2所示。

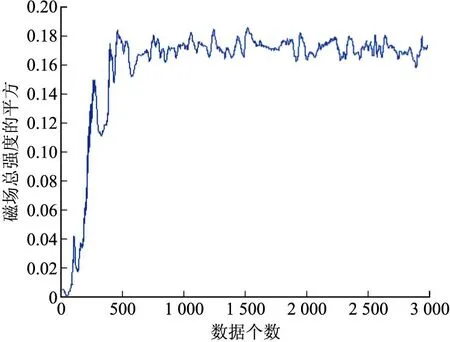
图2　无干扰条件下磁场总强度变化曲线平方

在三轴磁传感器系统的标定过程中,在一旁放置一块磁铁并不断改变磁铁的位置,用于施加一个变化的干扰磁场。在这种条件下,标定过程中采集到的数据绘图如图3所示。

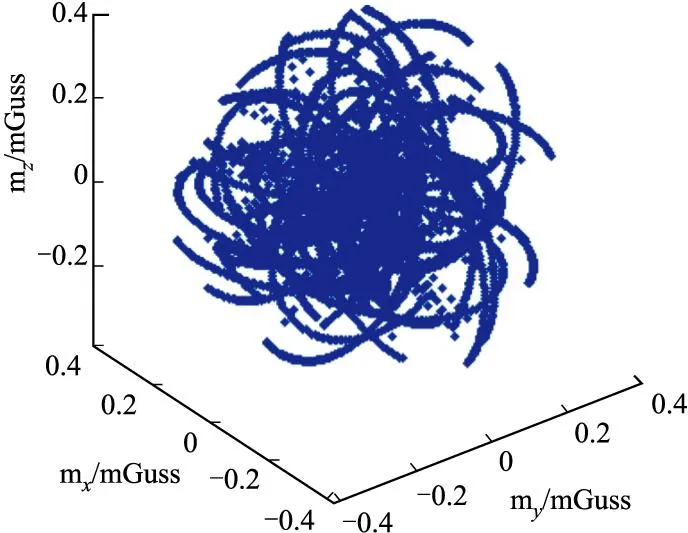
图3　干扰条件下三轴磁场数据情况

在外界磁场不稳定的条件下,标定过程中磁场总强度平方的计算值绘图如图4所示。

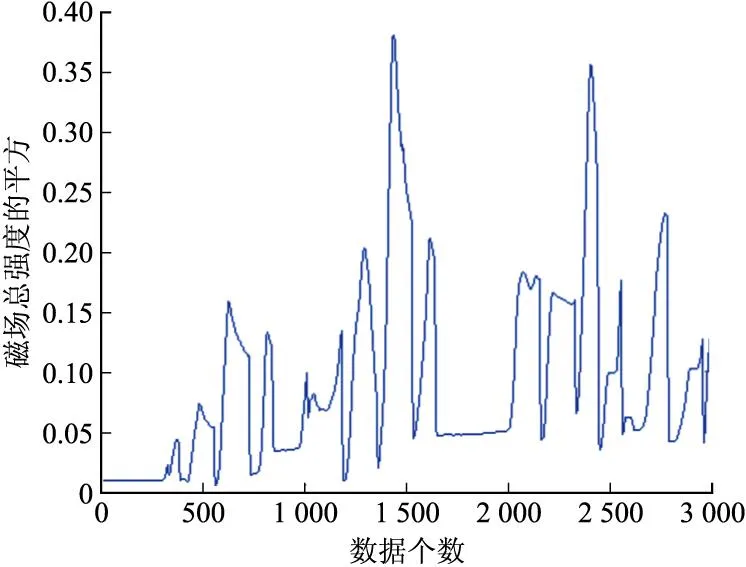
图4　干扰条件下磁场总强度平方变化曲线

为了验证三轴磁传感器系统的标定效果,利用其测量得到的三轴磁场值计算出载体的航向。将三轴磁传感器系统安装在无磁转台上,以其初始位置为起始位置,每旋转30°记录一次角度误差数据,直到旋转一周。记录数据绘图如图5所示。

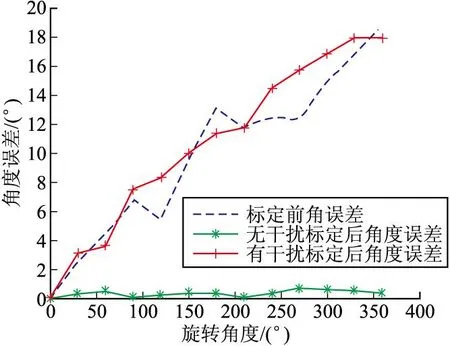
图5　三种条件下角度误差曲线

上图中数据显示三轴磁传感器系统测量得到的航向输出误差由18.7°减小到0.7°,表明三轴磁传感器系统在经过在线标定算法标定后,航向输出误差显著减小。在线标定算法成功的补偿了外界干扰对磁场测量的影响。

在未受到干扰的条件下,递推计算过程中的磁场总强度平方的计算值如图2所示,此时V的值为1.71×10-5。在外界磁场不稳定的条件下,标定过程中磁场总强度平方的计算值如图4所示,此时V的值为0.001 5。

经过大量的实验数据分析,V的值越小,标定参数的可靠性越高。在V的值小于1.0×10-4的情况下,标定参数在误差允许的范围内都是可靠的。V的值在一定程度上表明了标定结果的可信程度。

6结论

利用地磁场在小范围内短时间不变的特性,建立起椭球曲面模型对三轴磁传感器系统进行补偿,是一种十分有效的标定方法。但是由于其计算时需要大量的数据,限制了其应用范围。文中提出的以带约束的递推最小二乘法计算拟合椭球曲面参数的在线标定方法,克服了这种缺点,同时保证了在计算过程中参数的稳定性。相当于将整体计算拟合椭球曲面参数的过程拆分成一步一步进行,避免了计算参数时对其他设备的依赖,在避免标定精度降低的条件下实现了三轴磁传感器系统的在线标定,扩大了其使用范围,具有很强的实用性。同时文中提出在线标定参数质量的评价方法给出了一种标定参数有效性的初步评价标准,能够及时的发现标定过程中是否受到干扰。实验结果证明了在线标定算法的有效性以及标定参数质量评价的有效性。

参考文献:

[1]Qi Zhang, Qixiao Gao, Yongbing Chen. A novel magnetic compass calibration method based on improved ellipse model [C]∥International Conference on Intelligent Control and Information Processing, 2010: 11-15.

[2]Chao Hu, Tongxing Ma. Sensor arrangement optimization of magnetic localization and orientation system [C]∥ Proceedings of the 2007 IEEE International Conference on Integration Technology, 2007: 311-315.

[3]Wei Chen, Ruizhi Chen, Yuwei Chen. An adaptive calibration approach for a 2-axis digital compass in a low-cost pedestrian navigation system [C]∥Proceedings of the 2010 IEEE International Conference on Instrumentation and Measurement Technology, 2010: 1392-1397.

[4]郭鹏飞, 任章, 邱海韬. 一种十二位置不对北的磁罗盘标定方法 [J]. 中国惯性技术学报, 2007, 15(5): 598-601.

[5]朱建良, 王兴全, 吴盘龙. 基于椭球曲面拟合的三位磁罗盘误差补偿算法 [J]. 中国惯性技术学报, 2012, 20(5): 562-566.

[6]范玉宝, 李杰, 张晓明. 基于椭球拟合的微惯性测量组合现场快速标定方法 [J]. 传感技术学报, 2011, 24(11): 1547-1550.

[7]孙宏伟, 房建成, 李艳. 椭圆拟合方法在磁罗盘罗差校准中的应用 [J]. 光学精密工程, 2009, 17(12): 3034-3038.

[8]Andrewfitzgibbon, Mauriziopilu, Robertb. DirectLeast Square Fitting of Ellipses [J]. Pattern Analysis And Machine Intelligence, 1999, 21(5): 476-480.

[9]Nikosgrammalidis, Michaelg Strintzis. Direct least square fitting of ellipsoids [C]∥International Conference on Pattern Recognition, 2012: 3228-3231. Zhang, Qixiao Gao, Yongbing Chen. A novel magnetic compass calibration method based on improved ellipse model [C]∥International Conference on Intelligent Control and Information Processing, 2010: 11-15.

[2]Chao Hu, Tongxing Ma. Sensor arrangement optimization of magnetic localization and orientation system [C]∥ Proceedings of the 2007 IEEE International Conference on Integration Technology, 2007: 311-315.

[3]Wei Chen, Ruizhi Chen, Yuwei Chen. An adaptive calibration approach for a 2-axis digital compass in a low-cost pedestrian navigation system [C]∥Proceedings of the 2010 IEEE International Conference on Instrumentation and Measurement Technology, 2010: 1392-1397.

[4]郭鹏飞, 任章, 邱海韬. 一种十二位置不对北的磁罗盘标定方法 [J]. 中国惯性技术学报, 2007, 15(5): 598-601.

[5]朱建良, 王兴全, 吴盘龙. 基于椭球曲面拟合的三位磁罗盘误差补偿算法 [J]. 中国惯性技术学报, 2012, 20(5): 562-566.

[6]范玉宝, 李杰, 张晓明. 基于椭球拟合的微惯性测量组合现场快速标定方法 [J]. 传感技术学报, 2011, 24(11): 1547-1550.

[7]孙宏伟, 房建成, 李艳. 椭圆拟合方法在磁罗盘罗差校准中的应用 [J]. 光学精密工程, 2009, 17(12): 3034-3038.

[8]Andrewfitzgibbon, Mauriziopilu, Robertb. DirectLeast Square Fitting of Ellipses [J]. Pattern Analysis And Machine Intelligence, 1999, 21(5): 476-480.

[9]Nikosgrammalidis, Michaelg Strintzis. Direct least square fitting of ellipsoids [C]∥International Conference on Pattern Recognition, 2012: 3228-3231.

收稿日期:2014-06-12

基金项目:国家自然科学基金(61274117);国防技术基础科研(JSJC2013601C005)资助

作者简介:盛蔚(1972-),女,陕西西安人,教授,研究方向:硅MEMS惯性传感器与微小型导航、制导与控制系统。

中图分类号:V241.61

文献标志码:A

An On-line Calibration Method of Three-axis Magnetic Sensor System

SHENG Wei,JIANG Yong

(School of Instrument Science and Opto-electronics Engineering, BUAA, Beijing 100191, China)

Abstract:Available calibration methods for three-axis magnetic sensor systems overclaim for equipment, systems cannot complete calibration independently. Regarding the situation, an online calibration method was proposed. With this method, three-axis magnetic sensor system could complete calibration independently. A method for evaluating credibility of the online calibration parameters was also put forward in the paper. The validity of the online calibration method and online calibration parameter evaluation method was proved to be effective by a series of experiments.

Keywords:magnetic sensor; online calibration; ellipsoid fitting; recursive least-squares method