多管火箭炮阻尼特性研究*

李　霞,毕世华,傅德彬,王新星,牛青林

(1　北京理工大学宇航学院,北京　100081;2　中国兵器工业导航与控制技术研究所,北京　100089)

多管火箭炮阻尼特性研究*

李霞1,毕世华1,傅德彬1,王新星2,牛青林1

(1北京理工大学宇航学院,北京100081;2中国兵器工业导航与控制技术研究所,北京100089)

摘要:多管火箭炮系统阻尼是系统动态响应的重要参数,对连射时序和射击间隔有着重要的影响。针对多管火箭炮的典型结构,从理论上分析了影响系统阻尼特性的典型因素,运用多体动力学方法建立的计算模型进行仿真分析,仿真结果与理论分析一致。研究结果表明发射装置起落架与回转体间约束副的摩擦效应、起竖油缸阻尼效应、部件的弹性变形对多管火箭发射时的阻尼特性有着决定作用,而金属结构的材料阻尼特性对发射时的系统阻尼影响较小。

关键词:多管火箭炮;振动响应;阻尼特性;多体动力学

0引言

多管火箭发射时,定向管受到弹管碰撞接触以及发动机喷出的燃气射流冲击等共同作用,使得管口产生显著的振动响应。火箭弹脱离定向管约束后,振动响应的衰减速率主要由系统阻尼特性决定,进而决定多管火箭炮的连射射序和射击间隔,因此,对多管火箭发射装置的阻尼特性进行深入研究是有必要的。

针对多管火箭发射装置的振动问题,不少学者从振动控制的角度出发,开展了较多研究。例如,徐振钦等[1]针对多管火箭炮采用复合阻尼钢板连接回转体与底盘、摇架与发射箱,以实现多管火箭炮减振设计;此外,徐振钦等[2]还利用多管火箭高低机和方向机液压系统变刚度与阻尼技术实现发射装置振动控制;陈兵等[3]针对多管火箭炮对回转和俯仰部分利用变电磁阻尼实现定向器的振动控制。这些研究大多从不同角度出发增加发射装置的系统阻尼,以达到控制系统振动响应的目的,对影响系统阻尼特性的因素及多阻尼器间阻尼的传递关系等尚缺少全面的分析。

文中以多管火箭炮为对象,从起落架与回转体间约束副的摩擦效应、起竖油缸阻尼效应以及结构的材料阻尼等角度出发,分析发射系统阻尼特性的影响因素,并利用多体动力学方法仿真分析简化发射装置的阻尼特性,以进一步明确影响系统阻尼的关键因素。

1发射装置阻尼特性的理论分析

1.1　系统振动响应分析

多管火箭发射过程中,系统的振动响应一般可分为3个阶段[2]:1)受定向管约束期间,火箭弹在推力作用下向前运动,火箭弹与定向管碰撞接触,此时作用在发射装置上的激励主要为弹管间碰撞接触所产生的作用力,是瞬态激励作用下的强迫振动响应阶段;2)火箭弹后定向钮脱离定向管约束后,作用在发射装置上的弹管碰撞力为零,这时定向管受发动机喷出的燃气射流冲击作用,火箭炮依然处于强迫振动阶段;3)火箭弹飞行远离定向管,燃气射流冲击作用完全衰减后,火箭弹对火箭炮的作用力为零,火箭炮整体进入自由衰减阶段。

基于对发射系统响应的分析,在不考虑推力偏心、质量偏心及燃气射流冲击载荷作用等情况下,火箭弹脱离定向管约束后,外部激励为零,系统进行自由衰减振动,此时振动响应衰减速率主要由系统阻尼特性决定,系统阻尼增大,则衰减加速。

1.2　阻尼特性分析

2仿真分析模型

2.1　数学模型

基于发射装置的实际结构及运动情况,将发射装置简化为N个组件共同构成的多体系统。

对于多体系统的第i个柔体或刚体,其拉格朗日方程为[6]:

(1)

式中:T为柔体或刚体的动能;λ为拉氏乘子;Qj为广义力,包括单元弹性变形和外加载荷引起的广义力。

系统的约束方程:

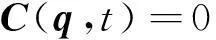
(2)

方程(1)和(2)构成系统的多体动力学方程。

为了验证理论分析结果并进一步明确发射装置的阻尼特性,利用ADAMS分别建立多刚体和刚柔耦合动力学模型,并对所建模型进行数值计算分析,其中柔性体的建立是在ANSYS中利用模态综合法生成模态中性文件,并导入到ADAMS中实现的。

2.2　仿真模型

多管火箭发射装置结构比较复杂,为研究发射装置的阻尼特性,在建立动力学模型时,必须对其进行适当的简化。根据系统各部件间运动关系,将该系统简化为与回转体一体固定的发射车、起落架、定向管、前中后3组定向钮及火箭弹5个部分。结构中的车体大梁长度较长,因此可将其作柔性体处理,起竖油缸及调平油缸柔性连接利用弹簧阻尼器来模拟,其它部分均视为刚体,因此可建立如图1描述的系统模型。基于图1的描述,分别建立多刚体动力学模型和以发射车为柔性体的刚柔耦合动力学模型,以此分析柔性体及结构阻尼对系统阻尼特性的影响。定向钮与定向管间的接触力主要采用基于Herz碰撞理论的接触算法[7]获得,接触参数与参与接触的部件的材料属性有关。参考软件经验值及文献[8-9],表1列出了接触主要参数值,并且起竖油缸的刚度系数设为20 kN/mm,调平油缸的刚度和阻尼系数分别设为25 kN/mm和50 N·s/mm。文中在不考虑推力偏心、质量偏心和燃气流作用等情况下,在常推力载荷激励下,就单发火箭弹发射时定向管管口的垂向位移振动响应进行分析,以基于对数衰减率法[10]获得的阻尼比来表征系统阻尼特性。

图1　多管火箭发射装置模型

刚度系数/(kN/mm)阻尼系数/(N·s/mm)幂指数静摩擦系数动摩擦系数2.211001.90.30.2

3影响系统阻尼比的因素分析

对多体动力学模型进行仿真,得到对应于不同起竖油缸阻尼系数、回转体与起落架间约束副摩擦系数和柔性体模态阻尼比的定向管管口垂向位移振荡曲线。从仿真结果可以看出,约束期内,随着火箭弹向前移动,定向管管口先下沉至最大下沉量后逐渐回弹,至火箭弹滑离定向管后,外部激励为零,此后发射装置进入自由振动响应阶段,并且响应幅值在自身阻尼特性作用下最终趋于收敛,但由于发射装置总重量减小,发射装置无法再回复到原状态。

本节利用上述仿真计算模型,结合不同的参数设置分析系统阻尼特性的影响因素。

3.1　起竖油缸阻尼系数对系统阻尼比的影响

图2描述了在回转体与起落架间理想转动副的约束下,起竖油缸阻尼系数从20~200 N·s/mm变化时多刚体模型管口垂向位移振荡曲线,从图中可以看出,起竖油缸阻尼系数增大,定向管管口垂向位移幅值(与平衡位置的相对位移的绝对值)减小,响应周期变化小,且随着时间的增加,幅值下降速度加快,以阻尼系数分别为20 N·s/mm和100 N·s/mm的振荡曲线中火箭弹离筒后出现的第三个最大正向峰值A3为例分析,阻尼系数增加4倍,幅值减小31.34%。

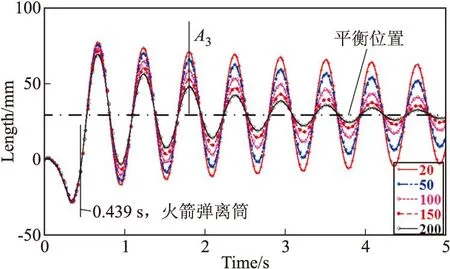
图2　不同起竖油缸阻尼下多刚体模型的管口垂向位移曲线

3.2　约束副摩擦系数对系统阻尼比的影响

图3给出了在起竖油缸阻尼为零的前提下,约束副静摩擦系数分别为0.1、0.15、0.3、0.5、0.6时相应的多刚体模型管口垂向位移振荡曲线,此时相对应的动摩擦系数分别为0.05、0.1、0.2、0.3、0.4,易知,静摩擦系数增大,定向管管口垂向位移幅值减小,且随着时间的增加,幅值的减小速度加快。同样的,以约束副静摩擦系数分别为0.1和0.5时曲线中的峰值A3为例,约束副静摩擦系数增加4倍,幅值减小66.67%。

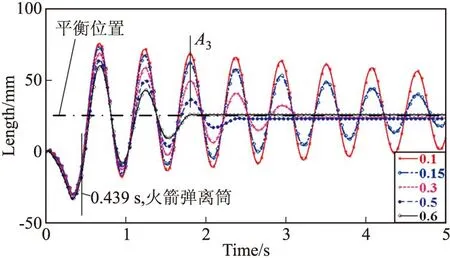
图3　不同约束副摩擦系数下多刚体模型的管口垂向位移曲线

从图2、图3中可以看出,系统响应周期变化较小,这主要是由于系统阻尼比相对于系统固有频率小得多,自由振动响应周期主要受固有频率的影响。

由以上分析可知,随着起竖油缸阻尼系数或起落架与回转体间约束副静摩擦系数的增大,则定向管管口垂向位移振荡衰减加速,系统阻尼比增大,且约束副摩擦阻尼对阻尼比的影响较起竖油缸阻尼大,与理论分析相一致。

3.3　结构柔性变形对系统阻尼比的影响

图4描述了在起竖油缸阻尼系数为100 N·s/mm和理想约束副的前提下,多刚体模型与刚柔耦合模型的定向管管口垂向位移响应曲线,易知,柔性体的加入使得定向管管口垂向位移幅值增加,以峰值A3为例,与多刚体模型相对比,加入柔性体的模型的定向管管口垂向位移幅值增加57.32%,并且刚柔耦合模型的系统振动响应明显滞后于多刚体模型,这主要是由柔性体的弹性变形造成的,与文献[11]结果一致;图5给出了在不计约束副摩擦阻尼和起竖油缸阻尼时,柔性体模态阻尼比分别为0、0.02、ADAMS软件缺省值[12]、0.08和0.1时的定向管管口垂向位移响应曲线,易从图中看出,不同模态阻尼比下的位移响应衰减均较小,且响应周期不变,以峰值A3为例,模态阻尼比增加4倍(0.02~0.1)时,幅值减小2.15%。由于模态阻尼比是物体材料阻尼的一种表征形式[13],故柔性体材料阻尼的变化对系统振动响应幅值和周期影响小,与理论分析相符。

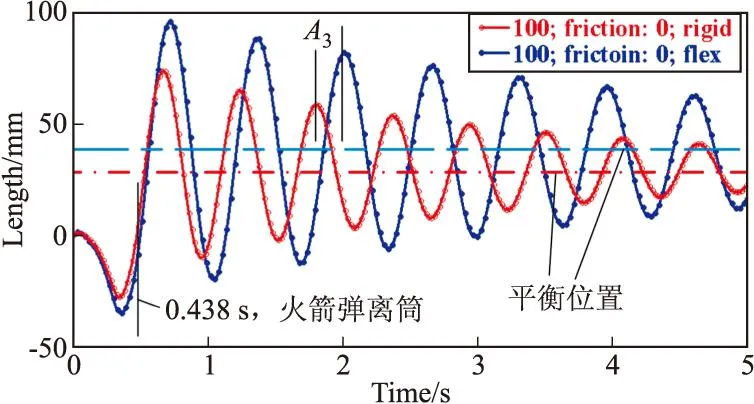
图4　基于多刚体模型与刚柔耦合模型的管口垂向位移曲线

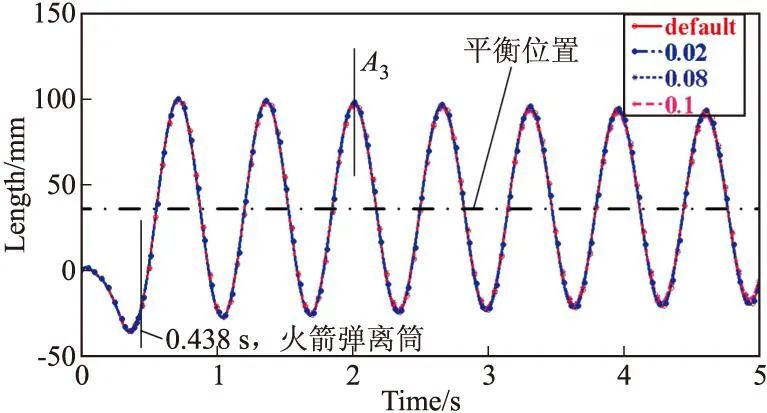
图5　不同柔性体模态阻尼比下的管口垂向位移曲线

3.4　影响系统阻尼比的典型因素

图6描述了起竖油缸阻尼系数分别为20 N·s/mm、100 N·s/mm时,约束副静摩擦系数从0变化至0.6时多刚体模型与刚柔耦合模型的阻尼比值,其中柔性体模态阻尼比设为ADAMS缺省值[12]。从图中可知,在同一起竖油缸阻尼和约束副摩擦系数条件下,加入柔性体的动力学模型比多刚体模型的阻尼比小,这主要归因于柔性体的弹性变形。由仿真结果知,起竖油缸阻尼系数为100 N·s/mm,约束副静摩擦系数为0.15时,刚柔耦合模型的系统阻尼比为0.051,多刚体模型的系统阻尼比为0.087。

图6　基于多刚体模型与刚柔耦合模型的阻尼比

起竖油缸阻尼系数/(N·s/mm)总体阻尼比206.57×10-31002.14×10-2相对变化量/%226

表3　起落架与回转体间约束副摩擦阻尼的影响

表2、表3分别为对应约束副零摩擦时不同起竖油缸阻尼、起竖油缸零阻尼时起落架与回转体间约束副摩擦阻尼的刚柔耦合模型的阻尼比,从这两个表中可以看出,约束副摩擦阻尼为0时,起竖油缸阻尼系数增加4倍,此时刚柔耦合模型的阻尼比增加2.26倍;起竖油缸阻尼为0时,约束副静摩擦系数增加4倍,刚柔耦合模型的阻尼比增加3.69倍,表明约束副摩擦阻尼对阻尼比的影响较起竖油缸阻尼大。

仿真结果表明,结构的材料阻尼对系统的阻尼特性影响较小,而起竖油缸阻尼、起落架与回转体间约束副摩擦效应及柔体的弹性变形影响较大,且约束副摩擦阻尼对阻尼比的影响较起竖油缸阻尼大,验证了理论分析的可靠性,并明确了系统振动响应的影响因素,具有一定的工程意义。

4结论

系统阻尼特性对多管火箭炮的连射射序和射击间隔的确定有着重要的影响。文中从力学理论出发,分析了多管火箭发射时影响系统阻尼特性的典型因素,并建立了多刚体动力学和刚柔耦合动力学模型进行计算分析,获得如下结论:

1)发射装置起落架与回转体间约束副的摩擦效应、起竖油缸阻尼系数和柔性体的弹性变形对多管火箭发射时的阻尼特性有着决定作用,而金属结构的材料阻尼特性对发射时的系统阻尼影响较小;

2)起竖油缸阻尼系数或起落架与回转体间约束副静摩擦系数增大时,定向管管口扰动衰减加快,系统阻尼比增大,且约束副摩擦阻尼对系统阻尼比的影响较起竖油缸阻尼大;柔性体的加入减缓了定向管管口扰动的衰减速度,其材料阻尼对系统阻尼影响较小。

参考文献:

[1]徐振钦, 马大为, 乐贵高, 等. 箱式火箭炮系统阻尼减振仿真分析 [J]. 弹箭与制导学报, 2005, 25(2): 77-79.

[2]徐振钦, 冯勇, 于存贵. 发射装置冲击振动的液压系统变阻尼控制 [J]. 机床与液压, 2009, 37(10): 106-109.

[3]陈兵, 马大为, 乐贵高. 多管火箭系统变阻尼振动控制研究 [J]. 弹箭与制导学报, 2006, 26(1): 763-765.

[4]胡海岩. 机械振动基础 [M]. 北京: 北京航空航天大学出版社, 2005: 7-13.

[5](美)SILVA C W D. 振动阻尼、控制和设计 [M]. 李惠彬, 张曼, 等译. 北京: 机械工业出版社, 2013: 1-8.

[6]冯勇, 马大为, 薛畅, 等. 多管火箭炮刚柔耦合多体发射动力学仿真研究 [J]. 兵工学报, 2006, 27(3): 545-548.

[7]徐振钦, 马大为, 乐贵高. 基于碰撞接触的弹管多体动力学建模与仿真 [J]. 系统仿真学报, 2007, 19(5): 965-968.

[8]陈余军, 姜毅. 车载导弹发射过程姿态模拟 [J]. 弹道学报, 2012, 24(1): 102-106.

[9]傅德彬. 数值仿真及其在航天发射技术中的应用 [M]. 北京: 国防工业出版社, 2011: 238-280.

[10]王宝元, 衡刚, 周发明, 等. 炮塔转动阻尼系数试验测试技术 [J]. 火炮发射与控制学报, 2013(1): 67-70.

[11]殷增振, 毕世华. 车载导弹多柔体发射动力学仿真研究 [J]. 弹箭与制导学报, 2009, 29(2): 183-185.

[12]李军, 邢俊文, 覃文洁. ADAMS实例教程 [M]. 北京: 北京理工大学出版社, 2002: 191-194.

[13]梁超锋, 欧进萍. 结构阻尼与材料阻尼的关系 [J]. 地震工程与工程振动, 2006, 26(1): 49-55.

收稿日期:2014-05-26

作者简介:李霞(1989-),女,湖南人,硕士研究生,研究方向:发射动力学与振动控制。

中图分类号:TJ393

文献标志码:A

A Study on Damping Characteristics of Multiple Launch Rocket System

LI Xia1,BI Shihua1,FU Debin1,WANG Xinxing2,NIU Qinglin1

(1School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;

2China Institute of Weapon Industry Navigation and Control Technology, Beijing 100089, China)

Abstract:The damping of multiple launch rocket system (MLRS) is key parameter of dynamic responses, which influences firing orders and firing interval. For typical structure of MLRS, typical factors of its damping characteristics were analyzed theoretically and the numerical models based on multi-body dynamics method were simulated. The simulation results are consistent with theoretical analysis. The results show that friction in the joint between landing gear and rotary body, erecting cylinder damping and the deformation of flexible bodies are decisive factors of the damping characteristics, while material damping of the metal structure has little effect.

Keywords:multiple launch rocket system (MLRS); vibration response; damping characteristics; multi-body dynamics