一类带脉冲呼吸系统疾病模型的周期解的存在性

曾晓云, 侯成敏, 胡正高

( 1.海军航空工程学院 系统科学与数学研究所, 山东 烟台 264001; 2.延边大学理学院 数学系, 吉林 延吉 133002; 3.海军航空工程学院 控制工程系, 山东 烟台 264001 )

一类带脉冲呼吸系统疾病模型的周期解的存在性

曾晓云1, 侯成敏2*, 胡正高3

( 1.海军航空工程学院 系统科学与数学研究所, 山东 烟台 264001; 2.延边大学理学院 数学系, 吉林 延吉 133002; 3.海军航空工程学院 控制工程系, 山东 烟台 264001 )

研究了具有脉冲效应的呼吸系统疾病模型,首先运用不等式技巧给出了该系统解的先验上界估计,其次运用迭合度理论中的延拓定理,得到了该系统至少存在一个正周期解的充分条件.

脉冲; 正周期解; 迭合度; 呼吸系统

1 问题的提出

Mackey等[1]将非线性时滞微分方程

(1)

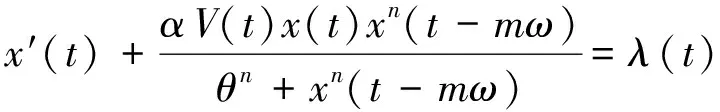
(2)

其中m与n是正整数, V与λ是周期为ω的正周期函数，并得到了方程(2)正周期解存在和全局吸引的充分条件.事实上,任何生物或环境参数都随时间变化,假设时滞是常数并不现实.基于此，Chen等[3]给出了方程(2)的修正形式：

(3)

并得到了方程(3)正周期解存在和全局吸引的充分条件.在生态系统变化过程中,许多进化过程经过一段平稳变化后会发生突变，如年度捕获和放养的物种以及年度迁移的物种等，于是学者们引入了脉冲微分方程[4].考虑到环境的周期性及脉冲扰动的影响,本文研究下述具有脉冲效应的呼吸系统疾病模型：

(4)

并对系统(4)做如下假设：

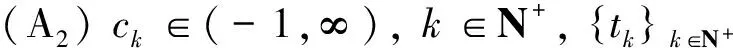
基于生物学意义,只需考虑系统(4)的正解.作变换x(t)=1/y(t), 则系统(4)化为下述非线性时滞脉冲微分方程

(5)

2 主要结果及其证明

定义1 称函数y∈([-τ,∞),(0,∞))是系统(5)在[-τ,∞)的一个解,若满足:

(i) y(t)在(0,t1]上且在每个区间(tk,tk+1]上绝对连续,其中k=1,2,…;

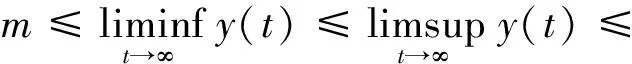
引入下列引理：

引理1[5]集合F⊂PC([0,T],Rn)是相对紧的当且仅当：

(i) F是有界的,即对每一x∈F和常数l>0, 有‖x‖≤l;

(ii) F在区间[0,T]上是拟等度连续的.

定理1 对系统(5)的初值φ(0)>0来说,系统(5)的所有解满足y(t)>0.

证明 对∀t>0, 存在k∈N, 使t∈(tk-1,tk], 并且有

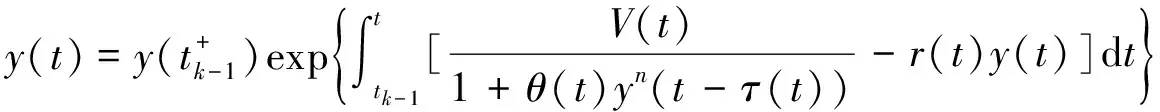
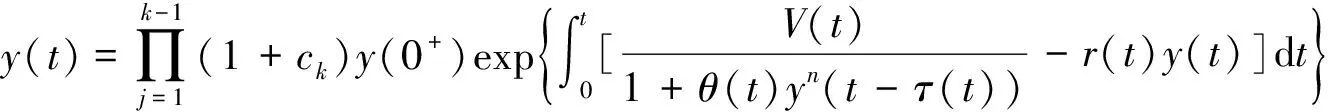
定理2 若条件(A1)和(A2)成立,且满足以下条件:

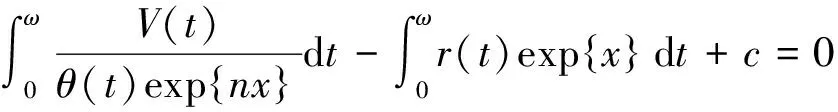
则系统(5)至少存在一个正ω-周期解.

证明 由定理1知系统(5)的所有解y(t)>0, 因此可对系统(5)做如下变换：

(6)

从而系统(5)变成如下形式

(7)

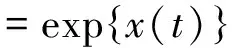
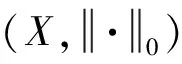
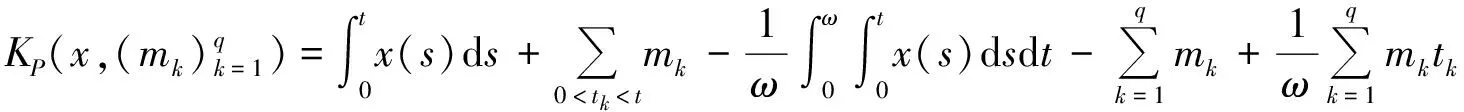
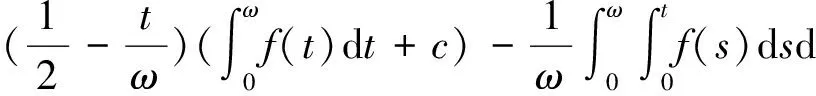
下面寻找满足引理1的合适有界开子集Ω.考虑算子方程Lx=λNx, λ∈(0,1), 即

(8)

假设对λ∈(0,1), x∈X是方程(8)的解,在区间[0,ω]上对方程(8)积分可得

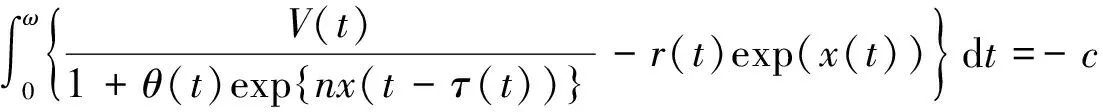
从而

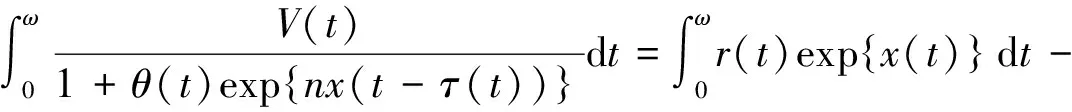
(9)

由(8)和(9)式可得

即

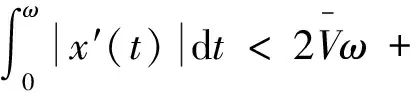
(10)

进一步,对任意ζ∈[0,ω]有下述不等式成立：

(11)

(12)

由于x∈X, 从而存在ξ,η∈[0,ω]使得

(13)

因此,从(9)和(13)式可得

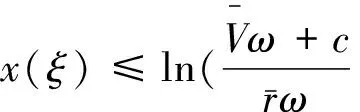
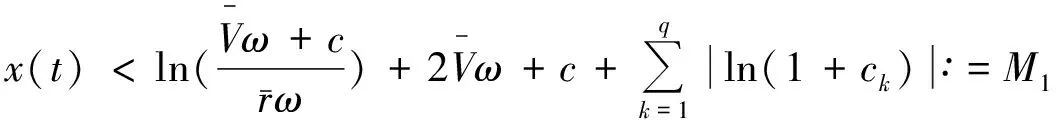
(14)

进而,由(9)和(13)式可得

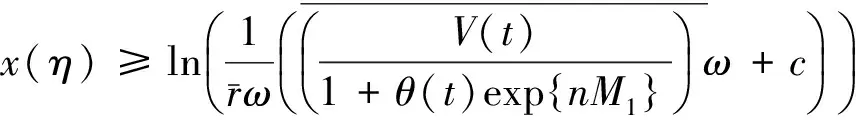
(15)

由(14)和(15)式可得

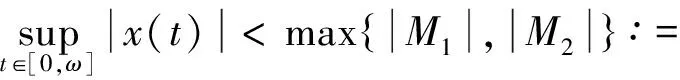
(16)

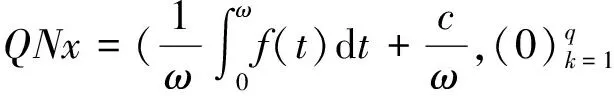
定义φ∶Dom L×[0,1]→X为

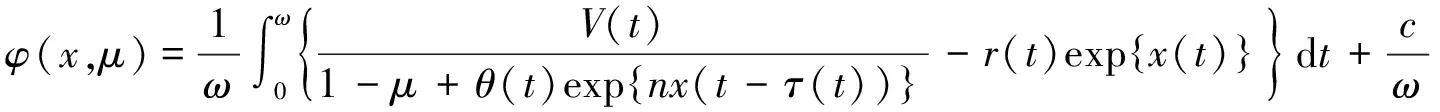
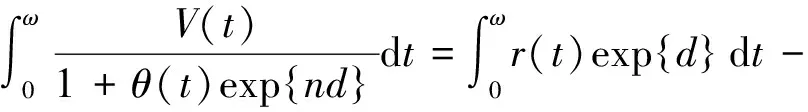
φ(x,μ)≠0,∀x∈(∂Ω∩Ker L)×[0,1].

因而Ω满足引理1的所有条件,所以系统(7)至少存在一个ω-周期解.由(6)式可知,系统(5)至少存在一个正ω-周期解.证毕.

[1] Mackey M C, Glass L. Oscillation and chaos in physiological control system[J]. Science, 1977,197:287-289.

[2] Saker S H, Agarwal S. Oscillation and global attractivity in a nonlinear delay periodic model of respiratory dynamics[J]. Comput Math Appl, 2002,44(5/6):623-632.

[3] Chen Y, Huang L. Existence and global attractivity of a positive periodic solution of a delayed periodic respiration model[J]. Computers and Mathematics with Applications, 2005,49(5):677-687.

[4] Bainov D, Simeonov P. Impulsive Differential Equations: Periodic Solutions and Applications[M]. Harlow: Longman Scientific & Technical, 1993.

[5] Sun T, Xi H. Global attractivity for a family of nonlinear difference equations[J]. Appl Math Lett, 2007,20(7):741-745.

[6] Wang W T. Positive pseudo almost periodic solutions for a class of differential iterative equations with biological background[J]. Appl Math Lett, 2015,46:106-110.

[7] Zhang H, Wang L, Yang M. Existence and exponential convergence of the positive almost periodic solution for a model of hematopoiesi[J]. Appl Math Lett, 2013,26:38-42.

Existence of periodic solutions for a respiratory diseases model with impulse

ZENG Xiaoyun1, HOU Chengmin2*, HU Zhenggao3

( 1.InstituteofSystemsScienceandMathematic,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China; 2.DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China; 3.DepartmentofControlEngineering,NavalAeronauticsandAstronauticsUniversity,Yantai264001,China)

A respiratory diseases model with impulsive effects is investigated in this paper. A prior upper bound estimation for the solution of the system is given firstly. Using Gaines and Mawhin’s continuation theorem from coincidence degree theory, we obtain the sufficient condition which ensures the system have at least one positive periodic solution.

impulse; positive periodic solution; coincidence degree; respiratory dynamics

2014-12-11 基金项目： 国家自然科学基金资助项目(11161049)

1004-4353(2015)01-0005-05

O175.13

A

*通信作者： 侯成敏(1963—)，女，教授，研究方向为微分方程理论及其应用.