基于ARIMA模型的银行贷款利率分析

邓浒楠，张 琼

（广东省交通运输规划研究中心，广州 510101）

一、背景

贷款利率伴随着货币贷款而产生，是借款人向出借人在一段时间内让渡货币的使用权而对出借人支付的报酬。贷款利率作为国家货币政策调控的重要手段，贷款利率的高低受经济社会众多要素的制约，其变化亦对社会生产、人民生活有重大影响。因此，近现代经济学家在研究利率问题时也就特别关注各种变量以及整个经济的平衡关系。在西方经济学利率决定理论中先后出现过古典利率、凯恩斯的流动性偏好、新剑桥学派的可贷资金利率以及新古典综合派的IS—LM等。这些理论试图分析利率与决定要素的相互关系，在一段时间内较好地解释了利率的高低水平。

考虑到银行贷款利率影响因素众多，很难对各个因素在一个时间段(或未来一段时间)的发展水平进行一一统计(预测)，而且任何事物的变化都是联系的，这也大大增加了利率高低的分析难度。时间序列分析法是金融定量分析的主流方法之一，近代计量经济与金融市场的许多研究成果都是建立在时间序列分析的基础之上的，它仅对过去的数据进行分析，试图在最大程度的挖掘既有数据信息，以对未来短期进行预测，具有不用对相关因素进行预测的优点。论文以央行1991~2012年公布的五年期银行贷款基准利率为样本，利用时间序列分析方法对过去的银行贷款利率进行拟合，并对短期（2013年）的银行贷款利率进行预测。

二、ARIMA模型理论基础

对于平稳时间序列，通常有 AR(p)、MA(q)模型。AR(p)模型认为t时刻时间序列的数值是过去p个时刻时间序列的回归，t时刻预测值与实际值差值为一白噪声。MA(q)模型认为t时刻时间序列的数值仅为过去q个时刻及第t时刻共（q+1）个白噪声回归所得。ARMA(p,q)模型是综合AR(p)、MA(q)模型考虑的因素所得的模型。

对于通常的金融时间序列只有一小部分为平稳时间序列，绝大部分的时间序列为一非平稳时间序列。对于通常的非平稳时间序列对其进行d次差分后通常能转换为平稳的时间序列 ARMA(p，q)模型。ARIMA(p，d，q)模型综合了上述所考虑的因素。本次研究采用博克斯·詹姆斯提出的B-J方法，利用Eviews软件对1991~2012年五年期贷款基准平均利率进行拟合。B-J方法的建模思想大致可分为四个部分。

第一，检验序列的平稳性，如果序列是非平稳的，通过差分变换或其他变换使其成为平稳序列。

第二，通过计算描述序列特征的统计量确定ARMA模型的p值和q值。

第三，参数标定及显著性检验。

第四，对模型做进一步的诊断分析，以确保所得模型与所观察的统计数据相吻合。

三、ARIMA模型建立与检验

（一）平稳性检验

数据序列的平稳性主要依靠对统计量的检，其中单位根检验是针对宏观经济数据序列、货币金融数据序列中是否具有某种统计特性而提出的一种平稳性检验的特殊方法。

首先对1991~2012年五年期银行贷款利率进行平稳性检验，结果见表1。单位根检验结果表明，五年期银行贷款利率序列ADF绝对值（1.925119）在10%置信区间范围内仍小于临界值，即接受时间序列存在单位根的假设，这表明银行贷款利率时间序列是非平稳的。对处理后的银行贷款利率进行一次差分，在1%置信区间拒绝假设，基本可视为平稳时间序列（见表2）。

表1 利率单位根检验结果

（二）A R IM A模型识别

ARIMA模型的重点和难点是确定模型的阶数（即p、q值），目前主要利用的理论仍是基于ACF值和PACF值确定p值和q值的，见表3。

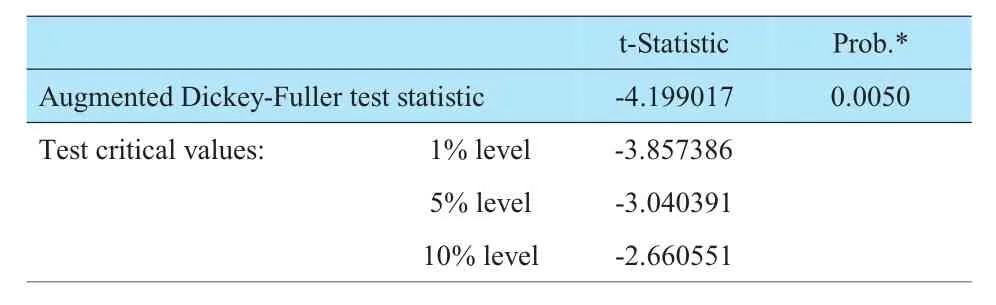
表2 一次差分后利率单位根检验结果

表3 ARMA(p，q)模型的ACF和PACF理论模型

从一阶差分后利率的自相关、偏相关函数图（图1）中可以看到，自相关函数和偏相关函数都是截尾的，差分后利率可认为服从ARMA模型的。对于自相关函数，5阶以后自相关函数明显下降，因此q值范围为1~5。对于偏相关函数图，4阶以后偏相关数值呈现出明显的截尾现象。因此，p值范围为1~4。

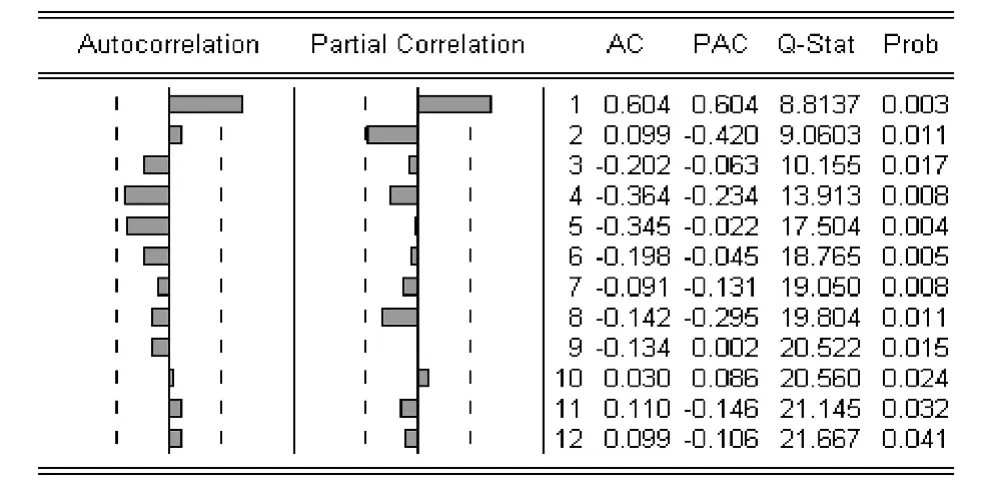
图1 一阶差分后利率自相关、偏相关函数图

（三）A R IM A模型标定及显著性检验

对于同一个序列，可能存在多个适应性模型，要从这多个适应性模型中选择，通常根据多个模型输出项中的赤池信息准则AIC(Akaike info criterion)和SC值进行比较，一般认为这两个统计量值越小的模型越好。同时，对于一个模型还应当考虑解释变量系数的显著性水平以及模型残差的平稳性情况。对p为1到4，q为1到5范围的ARMA模型进行标定，结果见表4。

表4表明，对于差分后的利率ARMA(1,1)、ARMA(1,2)、ARMA(2,2)、ARMA(2,3)、ARMA(3,1)五个模型的解释变量在15%显著区间范围内通过检验，其中以ARMA(2,2)、ARMA(3,1)两个模型的AIC值和SC值较小，见表5和表6。

进一步的，对这两个模型的残差进行分析，残差单根检验结果表明（分别见表7和表8），ARMA(2，2)模型的残差为非平稳序列，而ARMA(3，1)模型的残差是平稳的。

综合考虑，利用ARMA(3，1)模型对2013年贷款利率进行预测，预测结果见图2。

表4 ARMA(p，q)模型的检验值

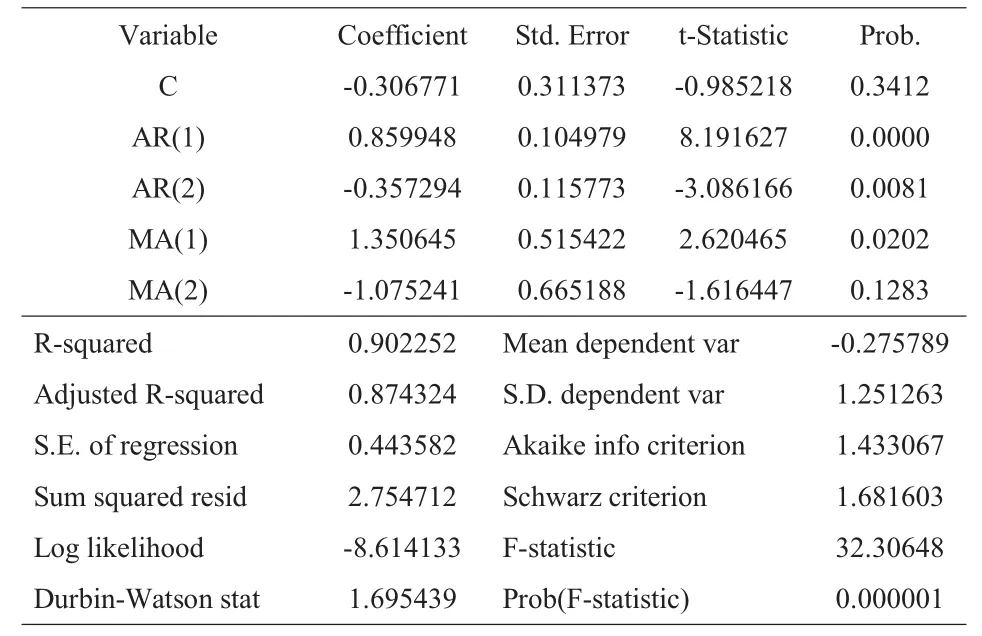
表 5 ARMA(2，2)模型标定值

表6 ARMA(3，1)模型标定值

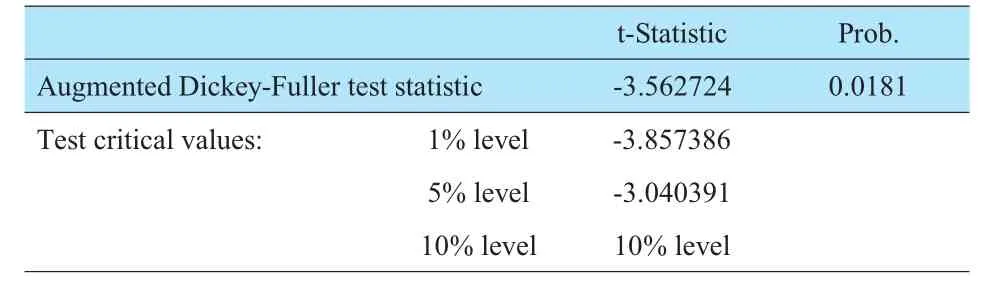
表7 ARMA(2，2)模型残差单根检验表

表8 ARMA(3，1)模型残差单根检验表

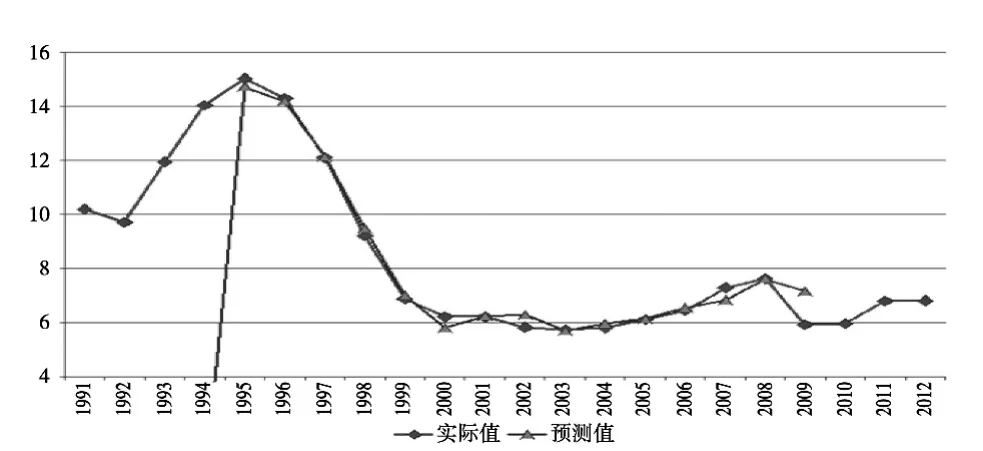
图2 基于ARIMA(3，1，1)模型的五年期贷款利率预测图

预测结果表明，模型预测值与偏差值最大的是2009年与2010年，偏差值分别为-1.22%和+1.01%，其余年份的偏差值均不超过0.5%，其中偏差绝对值在0%~0.1%、0.1%~0.2%、0.2%~0.3%、0.3%~0.4%、0.4%~0.5%范围内的分别为 6、4、1、4、2个，总体来说模型具有较好的拟合性质。模型预测2013年五年期贷款利率平均值为6.47%与2013年实际值偏差较小。

四、小结

论文尝试采用金融时间序列分析方法，以央行公布的1991~2012年五年期贷款基准利率数据为样本，利用Eviews软件对我国银行贷款利率进行分析研究。研究表明样本数据为非平稳时间序列，经一次差分后数据序列平稳，在模型识别、显著性检验以及残差分析基础上构建的ARIMA(3,1,1)模型拟合值与实际偏差绝对值在0%~0.1%、0.1%~0.2%、0.2%~0.3%、0.3%~0.4%、0.4%~0.5%范围内的分别为6、4、1、4、2个，且据此预测的2013年5年期贷款利率值与实际数据偏差0.08%。论文对银行贷款利率高低进行了一些有益的探索，构建的模型对样本数据具有较好的拟合效果。

[1] David Romer:Advanced Macroeconomics[M].University of Califomia,2006.

[2] Ruey S.Tsay:analysis of financial time series[M].2012.

[3]胡海鸥，贾德奎.“利率走廊”调控的理论与实践[M].上海：上海人民出版社，2006.

[4] 王文平.经济发展中的利率政策[M].北京：中国经济出版社，2005.

[5]丁 煜.利率趋势预测研究——基于综合模糊分析方法[D].济南：山东大学，2007.

[6] 宋保庄.我国利率的影响因素及其实证分析[D].郑州：河南大学，2008.

[7] 谭 莹.西方利率理论与中国利率市场化[D].广州：华南师范大学经济管理学院，2002(6).