基于Kent映射的混合混沌优化算法

刘建军，石定元，武国宁

（1.中国石油大学 理学院，北京102249；2.北京航空航天大学 电子信息工程学院，北京100191）

0 引 言

基本的混沌优化算法 （COA）［1－7］在搜索末期易陷入局部且收敛慢，因此，各种混合及改进混沌优化算法相继被提出，将混沌优化算法与梯度类算法结合［8，9］，改进混沌优化算法中初始变量的选取［10］等相结合后的混合算法均获得一些良好的效果。以上各种改进或混合算法仍存在不足之处，如基于梯度类混合算法要求目标函数可微等。为使算法中变量的分布具有更好遍历性、算法收敛快及得到高精度的全局最优解，本文在变尺度混沌优化算法的基础上，提出一种改进的混合混沌优化算法。改进算法既引入了遍历性更好的Kent映射来生成初始变量，又引入了稳定变化的尺度因子，在算法末期加入Nelder－Mead单纯形搜索策略，提高算法的收敛速度和解的精度。通过对一些典型测试函数进行数值比较实验，验证了改进算法的高效性。

1 Logistic映射与Kent映射的分布特征

现有的混沌优化算法及改进均采用Logistic映射生成新变量 （解），但Logistic映射的遍历性并不是最好的，从数学上讲，Kent映射与Logistic映射是同构的［11］，因此Kent映射也可用于随机优化算法中生成随机新解的方法，而Kent映射具有比Logistic映射更好的均匀遍历性，其迭代过程同样适合程序化运行。我们可以通过统计的方法说明Kent映射比Logistic映射好的遍历性。

由Logistic映射生成的混沌序列服从切比雪夫型分布，其概率密度函数具有边缘稠密、内部稀疏的特点，不利于搜索的效率和能力。Logistic映射的系统方程为

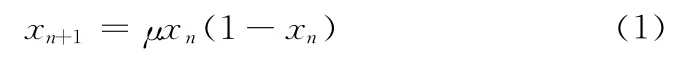
式中：μ——控制参数，取值范围为0＜μ ≤4。当μ ＝4时，该映射对应一种满映射混沌状态，此时的Lyapunov指数约等于0.691。在区间（0，1）内的概率密度函数为

Kent映射是另一个具有代表性且形式简单的离散混沌系统，其系统方程可表为如下形式

其中控制参数a∈（0，1），当a＝0.4时，其概率密度函数在（0，1）内服从均匀分布，即

此时，它的Lyapunov 指数约为0.696，大于经典的Logistic映射的0.691。而Lyapunov指数可以用来刻画初始状态微小不确定性的发散比率，因此，Kent映射比Logistic映射具有更好的遍历性。图1 是将Kent映射与Logistic映射各迭代20 000次得到的 ［0，1］上的概率分布直方图。图中显示Logistic 映射在区间 ［0，0.0125］和［0.9875，1］上取值概率较高。而Kent映射在各区间分布相对较均匀。

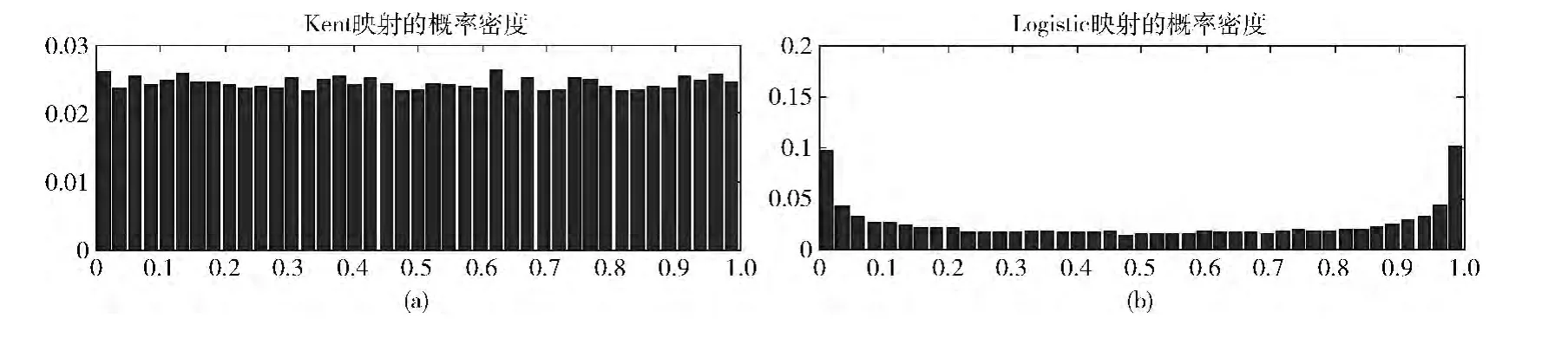
图1 Kent映射和Logistic映射的概率分布直方图

2 Nelder－Mead单纯形法

Nelder－Mead单纯形法是求解无约束优化的一种直接方法，由于它不需要目标函数的梯度信息，因此被广泛应用于不可微的连续函数优化及诸多启发式算法中［12］。单纯形法是在给定Rn中一个单纯形后，先计算出n＋1个顶点上的函数值，再找出最大函数值的点 （称为最高点）和最小函数值的点 （称为最低点），然后经过反射、扩展、压缩等过程，确定出一个较好点，最后用它取代最高点来构成新的单纯形，也可以通过向最低点收缩，形成新的单纯形。单纯形法即是通过构造一系列的单纯形来逼近极小点。

针对一般的无约束优化问题

下面给出Nelder－Mead单纯形法算法的步骤框架。

（1）构造初始单纯形。任意选取n＋1个不同的点并计算其函数值。通过比较这些值的大小，确定最高 （坏）点xh，最低 （好）点xl，次低 （坏）点xg，并且yh＝

（2）计算除xh以外的n 个点的中心点xc，即xc＝求出反射点xr＝xc＋α（xc－xh），其中α为反射系数，一般取值为1。计算函数值yr＝f（xr）；

（3）若yr≥yh，则进行压缩，并令压缩点xs＝xh＋λ（xr－xh）其中0＜λ＜1称为压缩因子；若ys≤yl，令xl＝xs，否则进行扩张，令扩张点xe＝xh＋μ（xr－xh）其中，μ＞1称为扩张因子。一般取1.2＜μ＜2。若ye≤yr，令xs＝xe，否则xs＝xr；

（4）若ys≤yg，则令xh＝xs。以新的xh与其它的n个点一起构成新的单纯形，重新确定xh，xl和xg，并重复前述步骤 （2）。否则进行下一步；

（5）单纯形向点xl收缩，令xi＝，i＝1，2，…，n。然后转向（1）。重复上述过程，直到满足停止条件｜yhyl｜≤ε，其中ε为预先给定的精度。

单纯形算法具有计算量小、收敛速度快且对优化函数要求低 （不要求可微）的特点，因此被应用于很多不可微函数优化问题中。单纯形法的不足之处是过分依赖于初始解的位置，容易陷于局部，很难搜索到全局最优解。因此，将单纯形法与混沌优化算法相结合，可以提高混沌优化算法的收敛速度和最优解的精度。

3 基于Kent映射的混合混沌优化算法

应用Kent映射、变尺度因子和单纯形算法，构造一种混合混沌优化算法 （KSCOA）。算法分为两个阶段，即粗搜索阶段和细搜索阶段。在粗搜索阶段使用Kent映射，以提高算法遍历搜索空间的能力。而细搜索阶段结合了变尺度方法和单纯形算法的优势，此阶段又分为前期和后期，即细搜索的前期利用变尺度方法的大区间上的寻优能力将最优解的搜索范围最终确定在一个小的区间上，然后在细搜索的后期利用单纯形算法的局部寻优能力以搜索到一个精度较高的最优解。本文的这种混合策略不但可以保证解的全局最优性，同时相较于传统的变尺度混沌方法具有更快的收敛速度和获得更高精度解的能力。

本文算法的步骤如下：

步骤1 初始化各项参数。

令flag1控制粗混沌迭代搜索进程，flag2控制细搜索前期的进程，flag3控制细搜索后期的进程。ε1和ε2分别表示细搜索的前期和后期的精度，fmin用于存储更新的函数极小值。初始混沌变量设为个m 具有微小差异的初值ci，i＝1，2，...，m。

步骤2 将混沌变量ci按式 （6）映射到函数优化变量的分量取值区间［ai，bi］

步骤3 粗搜索。开始混沌迭代搜索。

如果f（xi）＜fmin，则fmin＝f（xi），＝xi，否则利用Kent映射生成新混沌变量，即ci＝kent（ci），flag1：＝flag1＋1。转步骤2，如果flag1＞flag1max，转步骤4。

步骤4 细搜索。

（1）用变尺度法搜索。

如果｜br＋1i－｜≤ε1，转入 （2），否则，按式 （8）将当前解变换到［0，1］区间

（2）用Nelder－Mead单纯形算法搜索。

令x0＝为单纯形搜索初始点构造初始单纯形S0＝［V0，V1，…，Vn］，按第2 节方法进行反射、延伸、收缩搜索，得 Si＝ ［，…］。 令若，则x＊＝V ，fmin＝f（x＊）。转步骤5。

步骤5 输出最小值fmin，最优解x＊，算法终止。

在步骤4 （1）中，变尺度因子γ按式 （9）的选取，图2显示了变尺度参数 （因子）与细搜索次数的变化曲线，这种变化既保证算法前期收敛平缓又能使得γ在后期趋于一个较小的值从而使算法能够较快收敛

同时，算法在运行过程中，为保证区间缩小，必须要进行越界处理：若＜，则＝；若＞，则＝。

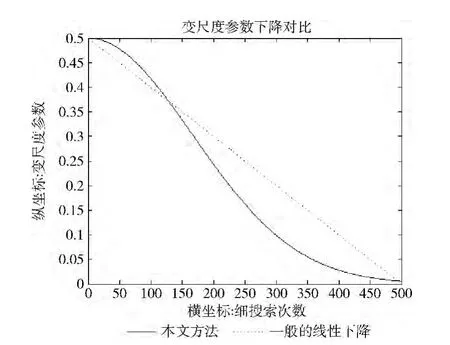
图2 变尺度参数变化曲线

4 算法性能测试与分析

为测试改进算法KSCOA 的运算性能，这里选用6 个常用于验证算法性能的典型测试函数进行实验，其中只有第6个函数Schaffer函数为2维，其它均为任意有限维。表1列出了6个测试函数的表达式、多或单峰性、取值区间及最优性情况。下面把本文改进算法与混沌优化算法的3个变种，即粗搜索阶段使用Logistic映射的传统变尺度混沌优化方法 （LCOA）、粗搜索阶段使用Kent映射的传统变尺度混沌优化方法 （KCOA）、粗搜索阶段用Logistic映射细搜索阶段用单纯形变尺度相结合方法 （LSCOA）的计算结果进行比较。

本文所用软件坏境为：Win7 （X64），Matlab 7.7，计算机硬件配置为：奔腾双核T3200主频2GHZ，内存2G。选取20个初始混沌变量c0（i）＝0.045i，i＝1，2，…，20，迭代次数设为1000。各算法均独立运行50次。

表2给出了测试函数选取2维时，比较Logistic映射和Kent映射构造的COA 算法的平均计算时间与函数平均值的比较结果。

从表2比较分析出，Kent映射虽然在时间复杂度上稍逊于Logistic映射，但前者所得的平均值明显优于后者，这是由于Logistic映射的遍历均匀性较差，概率密度函数决定绝大部分搜索点都分布在边界区域，如果全局最优解不在区间边界附近，则该映射的全局搜索效率将大为降低。而Kent映射对应的搜索点在搜索区间内分布较均匀，因此用Kent映射取代Logistic映射确实能提升算法的全局寻优能力。

Sphere函数是单峰函数，用它可以验证算法的收敛性，而Griewank函数是多峰函数的典型，用它可以验证算法的全局收敛性。因此，图3只绘出了4种算法针对Sphere函数与Griewank函数 （5维）在某次迭代过程中的收敛曲线。图3 （a）显示了对于单极值的连续函数，搜索末期使用单纯形算法相较继续使用变尺度方法来说明显加快了收敛。图3 （b）显示了对于多极值问题，本文方法仍具有收敛较快的优势。特别是对高维函数，变尺度混沌优化算法很难得到高精度解，但是只要加入单纯形法参与运行，则解的精度便会得到极大提高。

表1 测试函数

表2 Logistic与Kent的映射在粗搜索过程中的比较

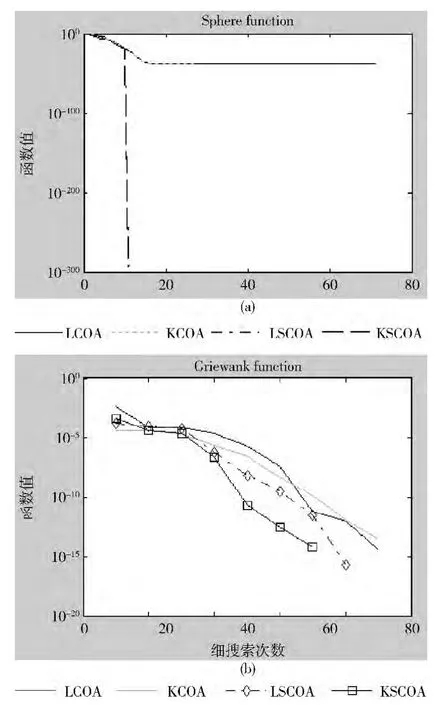
图3 4种算法对Sphere和Griewank函数的收敛曲线对比

表3 4种优化方法的数值运算结果比较

5 结束语

本文在变尺度混沌优化算法的基础上，构造了一种混合混沌优化算法。该算法主要有3个方面改进：①为了改善原算法的全局收敛性，本文用比传统的Logistic映射具有更好遍历性的Kent映射来生成随机的初始变量；②为避免算法早熟，引入了非线性的尺度变化因子；③为保证算法在运行末期取得更高精度的解，采用单纯形法进行搜索。数值实验结果表明，在混沌优化算法的粗搜索阶段，Kent映射的均匀遍历性提高了搜索到好解的可能性。而在细搜索法后期，改用单纯形法后比继续用变尺度的方法具有收敛快精度高的优点。总之，本文将Kent映射、单纯形方法及变尺度方法结合后得到的改良的混沌优化算法具备较高的速率和精度，是一种混沌算法的较好的改进，期望在实际应用中会有更好的效果。

［1］Yang D，Li G，Cheng G.On the efficiency of chaos optimization algorithms for global optimization ［J］.Chaos，Solitons ＆Fractals，2007，34 （4）：1366－1375.

［2］Tavazoei，Mohammad Saleh，Mohammad Haeri.An optimization algorithm based on chaotic behaviour and fractal nature［J］.Journal of Computational and Applied Mathematics，2007，206 （2）：1070－1081.

［3］Yuan XF，Li ST，Wang YN，et al.Parameter identification of electronic throttle using a hybrid optimization algorithm ［J］.Nonlinear Dyn，2011，63 （4）：549－557.

［4］Dos Santos Coelho L.Tuning of PID controller for an automatic regulator voltage system using chaotic optimization approach［J］.Chaos，Solitons ＆Fractals，2009，39 （4）：1504－1514.

［5］Khoa T Q D，Nakagawa M.Training multilayer neural network by global chaos optimization algorithms［C］//International Joint Conference on Neural Networks.IEEE，2007：136－141.

［6］YANG Lingling，MA Liang，ZHANG Huizhen.Chaotic optimization algorithm for multi－objective 0－1programming problem［J］.Application Research of Computers，2012，29 （12）：84－87（in Chinese）.［杨玲玲，马良，张惠珍.多目标0－1规划的混沌优化算法［J］.计算机应用研究，2012，29 （12）：84－87.］

［7］Ikeguchi T，Hasegawa M，Kimura T，et al.Theory and applications of chaotic optimization methods ［M］.Innovative Computing Methods and Their Applications to Engineering Problems.Springer Berlin Heidelberg，2011：131－161.

［8］Luo Y Z，Tang G J，Zhou L N.Hybrid approach for solving systems of nonlinear equations using chaos optimization and quasi－Newton method［J］.Applied Soft Computing，2008，8（2）：1068－1073.

［9］Yang D，Liu Z，Zhou J.Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization ［J］.Communications in Nonlinear Science and Numerical Simulation，2014，19 （4）：1229－1246.

［10］SU Youliang，ZHOU Dejian.Performance analysis of chaos immune evolutionary algorithm with different maps ［J］.Computer Engineering，2010，36 （21）：222－224 （in Chinese）.［苏有良，周德俭.不同映射的混沌免疫进化算法性能分析 ［J］.计算机工程，2010，36 （21）：222－224.］

［11］Tavazoei M S，Haeri M.Comparison of different one－dimen－sional maps as chaotic search pattern in chaos optimization algorithms［J］.Applied Mathematics and Computation，2007，187 （2）：1076－1085.

［12］Wang L，Xu Y，Li L.Parameter identification of chaotic systems by hybrid Nelder– mead simplex search and differential evolution algorithm ［J］.Expert Systems with Applications，2011，38 （4）：3238－3245.