融合ARIMA和RBFNN 的血糖预测

王延年，雍永强，贾晓灿，李全忠，孙长青＋

（1.郑州大学 信息工程学院，河南 郑州450001；2.郑州大学 公共卫生学院，河南 郑州450001；3.河南省人民医院 内分泌科，河南 郑州450003）

0 引 言

CGMS （continous glucose monitoring system）借助 埋在脐周皮下的探头检测葡萄糖浓度，能连续获得患者血糖的变化及波动。国内外学者基于CGMS所提供的数据，提出了多种预测方法，常见的有自回归 （auto－regressive，AR）模型、自回归移动平均 （auto－regressive moving average，ARMA）模型［3］、支持向量机［4］、极限学习机［5］、神经网络［6］等。这些方法都只利用CGMS所提供的数据，没有考虑外部因素 （饮食、药物注射、运动等）对人体血糖的影响。

S.Pappada等［7］提出的神经网络方法和Eleni I.Georga等［8］提出的支持向量回归方法不仅采用CGMS所提供的数据，而且结合了人体的生理模型。结合生理模型的预测方法考虑比较全面，但需要大量病理学和生理学的知识，所提算法和预测模型复杂庞大，预测有一定的延迟。

本文基于CGMS 所提供的血糖数据，提出一种融合ARIMA 和RBF神经网络模型预测血糖的综合预测方法。针对外部事件对血糖的影响，提出一种发现和处理算法，在血糖变化受外部因素影响时能自动调整未来一段时间内的血糖预测值，保障预测精度。

1 方 法

采用ARIMA 模型对未来血糖值进行预测，并计算出误差项，用RBFNN 算法对输入值、趋势值、预测残差、预测残差的趋势值等进行学习、网络训练与拟合，最后将ARIMA 计算出的预测值与RBF 算法得到的修正值组合得到准确的预测。同时针对外部因素对血糖变化的影响，提出一种发现和处理算法。

1.1 组合预测模型

融合ARIMA 和RBFNN 的组合预测模型的具体结构如图1所示。

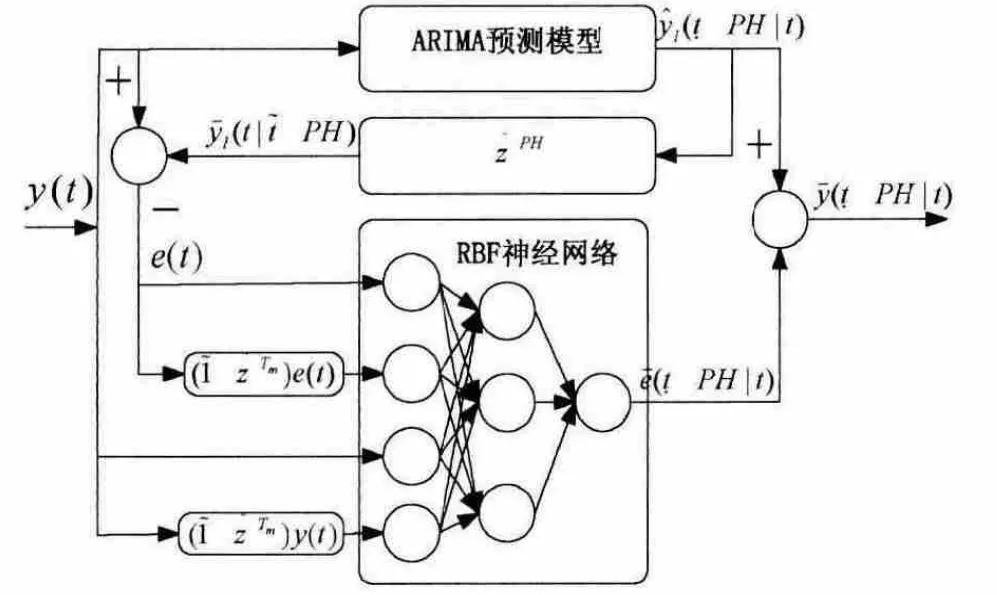
图1 融合ARIMA 和RBFNN 的组合预测模型

基于组合预测模型的血糖预测步骤为：

（1）用ARIMA 模型对从CGMS 采集到的血糖序列y（t）进行建模预测。PH 时间段后的预测结果为（t＋PH｜t）。

（2）利用 （1）得到结果得到ARIMA 产生的预测残差：e（t）＝y（t）－（t｜t－PH）。

（3）将e（T），（1－z－Tm）e（t），y（t），（1－z－Tm）y（t）作为RBFNN 的输入，得到PH 时间段后的预测结果（t＋PH ｜t）。

1.2 数据预处理

从CGMS采集的血糖数据由于存在噪声干扰需要进行平滑滤波处理。卡尔曼滤波具有计算量小、实时性高、效果好等优点，而且采用Kalman滤波对CGMS采集的数据进行平滑处理能有效地减少信号中的噪声，同时减少预测值和实际值之间的时延［9］。本文采用Kalman滤波对CGMS采集的数据进行平滑处理。

1.3 ARIMA模型

ARIMA 的一般表达式为

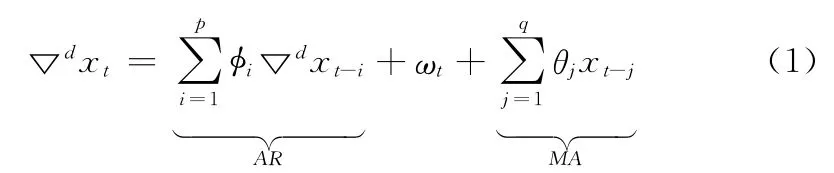
记作ARIMA（p，d，q），其中，xt是血糖值组成的时间序列，i 是自回归 （AutoregRessive，AR）项的参数，θj是滑动平均 （MovingAverage，MA）项的参数，ω为零均值及方差为δ2的高斯白噪声。用于对数据进行差分处理，可表示为

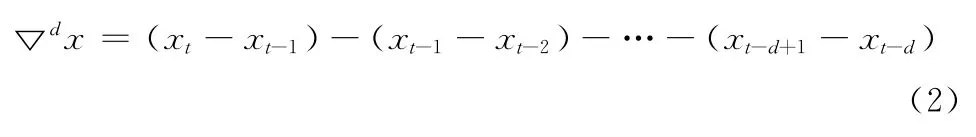
ARIMA 处理过程如下：

（1）由于血糖序列是一种非平稳时间序列，首先对它进行差分处理，即

那么血糖序列的ARIMA （p，d，q）模型为

其中，｛αt｝为白噪声序列。

（2）模型识别。p，d，q 的选择是ARIMA 建模的关键。首先对血糖数据进行差分处理，每次差分比较其自相关（auto correlation function，ACF）和偏自相关 （partial auto correlation function，PACF）组成的条形图，选择最佳的d。p，q的确定采用AIC （Akaiki information criterion）准则和BIC （Bayesian information criterion）准则［10］，计算AIC和BIC的方程如下［11］

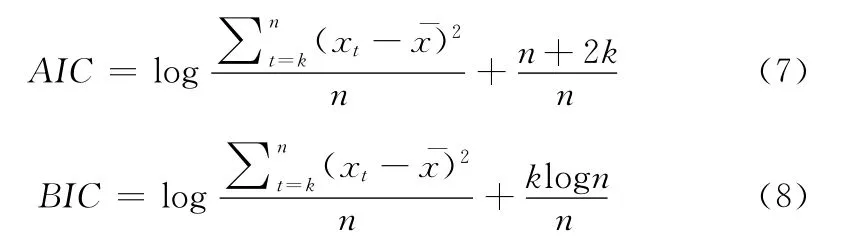
式中：k——参数模型的个数，n——样本数。

（3）估计参数并检验模型。模型中的所有参数的估计都采用极大似然估计法，然后进行检验。方法是检验误差序列是否具有随机性；如果检验通不过就继续进行识别。

（4）利用选中的最佳参数组成预测模型。ARIMA 模型采用已经采集到的在xt，xt－1，…xt－n时刻的血糖值，预测未来xt＋m时刻的血糖值。方程为xnn＋m＝E［xn＋m｜xn，xn－1，…，x1］。详细的过程可参考文献 ［12］。

1.4 RBF神经网络

对于线性时间序列，ARIMA 的预测简单精准。从CGMS收集到的血糖数据是线性的，但影响血糖变化的因素复杂多样。只使用线性预测模型会带来时延，影响预测的准确性。

RBF神经网络在处理非线性问题时能力很强。不仅学习速度快，且避免局部最小问题，只有少量权值需要调整。

RBF神经网络学习过程：

（1）利用高斯函数激励函数，输入和输出的非线性映射如下

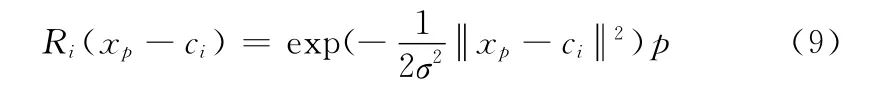
其中，xp＝（xp1，xp2，…xpn）T为第p个输入样本，ci为隐含层高斯函数的中心，σ为高斯函数的方差，为欧式范数。

（2）隐含层和输出层之间的线性映射，函数为

式中：h——隐含层的节点总数，ωij——隐含层到输出层的线性加权值，yi——网络中第j 个输出节点的实际输出，n——输出节点数。d为期望输出值，隐含层的σ可表示为

（3）参照样本数据，校正输出层和隐含层之间的参数。本文中RBF的输入包括4个部分：

（1）ARIMA 产生的预测残差

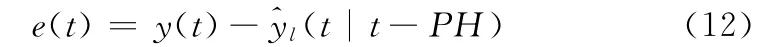
（2）ARIMA 预测残差的趋势（1－z－Tm）e（t）。

（3）目前的血糖值y（t），即从CGMS读取的数据。

（4）在时间步Tm目前的血糖趋势值（1－z－Tm）y（t）。

2 预测结果评价与分析

2.1 数据来源

本文所使用的血糖数据来自河南省人民医院，是对病人连续监测得到的，采用动态血糖监测系统 （CGMS）采集。CGMS每10秒中接收一次电流信号，每5分钟将获得的平均值转换成葡萄糖值储存起来，24小时共储存288个葡萄糖值，共持续监测72个小时。任意选取其中的24 个小时，其中前258个数据作为训练集，对血糖数据进行建模，采用最后30个样本作为测试集。24小时所采取的某病人的血糖值如图2所示。

2.2 ARIMA预测结果

将288个数据样本输入到MATLAB R2012A 中，采用ARIMA 的数据分析功能，得到血糖值自相关图和偏自相关图，如图3所示。从图3可知，血糖值序列有较高的自我相关性。需要进行差分处理，使血糖值序列变成平稳的时间序列。取差分阶数d＝1时，血糖序列基本平稳，所以最佳差分阶数为d＝1。其1阶偏相关图和自相关图如图4所示。

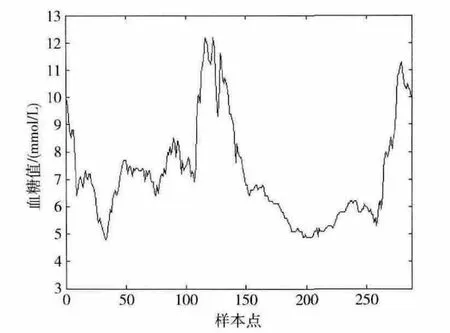
图2 24小时采取的病人的血糖值

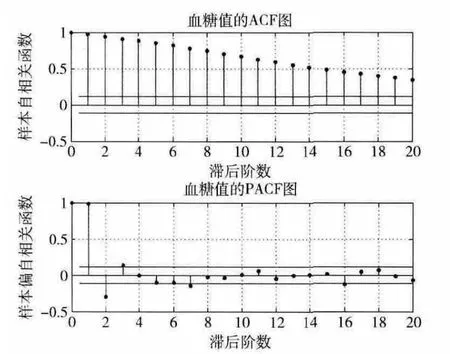
图3 血糖值的ACF图和PACF图

图4 1阶偏相关和自相关图

2.3 ARIMA模型参数的识别

采用从低阶到高阶逐步试探法来识别模型的参数，尝试采用不同的p和q值，比较AIC和BIC取得最小值。

从表1的模型指标对比可以看出，模型ARIMA （0，1，1）比较适合预测血糖值。采用一步预测法进行预测，预测结果如图5所示：ARIMA 模型用于对血糖的预测，能够好地把握血糖的变化趋势，但精度不高。

表1 血糖序列的AIC和BIC检测值

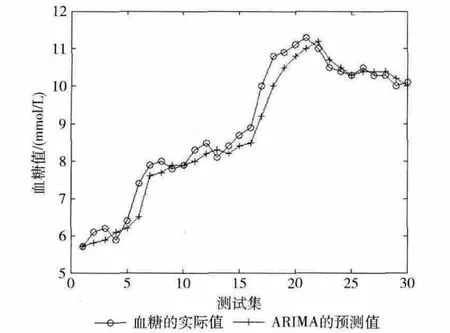
图5 ARIMA 模型的预测结果

2.4 ARIMA－RBF组合预测

根据ARIMA （0，1，1）预测结果和血糖实际值得到血糖值的残差序列，计算出ARIMA 预测误差的趋势和当前血糖值的趋势，结合当前的血糖值对RBF进行建模和训练，得到预测值。组合模型的预测结果如图6所示。

从图6可知，ARIMA－RBFNN 组合预测模型不仅能够准确把握血糖的变化趋势，而且能比较准确地预测出短时间能的血糖值。

2.5 模型预测性能对比

为了能评价和比较预测结果，本文使用两个性能指标

（1）均方误差 （mean squared error，MSE）

图6 ARIMA－RBFNN 组合预测结果

（2）平均绝对相对误差 （mean absolute error，MAE）

从表2的对比结果可知，ARIMA－RBFNN 的血糖预测精度要高于单一的ARIMA 模型的预测精度，预测误差有较大的降低，是一种有效的血糖预测方法。用ARIMARBFNN 模型进行血糖值的预测，只需要利用CGMS提供的历史数据，相对于结合各种生理模型的预测方法［5，6］，ARIMA－RBF神经网络组合预测算法简单可靠。

表2 两种预测方法误差分析

2.6 针对外部因素对血糖的影响的奇异点发现和处理算法

通过预测结果的观察，某些时刻预测值与真实值差距较大，经过分析研究，差距较大的时间段大多有饮食、胰岛素的注入、运动等事件的发生。如图7 所示。预测时间段受饮食的影响，饮食后的预测精度大大降低。

定义满足如下条件的点为奇异点

式中：threshold（k）——判定某点是否为奇异点的门槛，大小可调，当k时刻真实血糖值y（k）与预测的血糖值（k｜k－PH）满足上述条件时为奇异点。

通过实验和观察发现，奇异点一旦出现，将会持续3到5个采集点。可以在预测过程中不断加入实际血糖值来判断奇异点，为了提高预测的精度，提出了如下的算法：

（1）根据公式判断采集点是否是奇异点；

（2）如果是奇异点，将当前时刻未来4个时间段血糖预测更新为

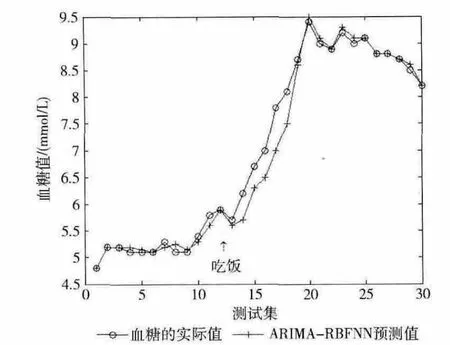
图7 受饮食影响的ARIMA－RBFNN 预测结果

（3）在发现奇异点时，其5个时间段后继续执行判断奇异点，如果再次发现，则回到 （1）；如果没有发现，则不做任何处理。

采用ARIMA－RBF预测模型对奇异点进行预测后的效果对比如图8所示，进行预测后的MSE 和MAE 为0.0069和0.0616，而不是改进前的0.0609和0.1416。

图8 改进后与改进前的对比

3 结束语

本文基于CGMS，提出一种融合ARIMA 和RBFNN 的组合预测模型，并与ARIMA进行对比。在组合预测的基础上，针对外部因素对血糖的影响，提出一种发现和处理算法，能够在血糖受外部因素影响时调整未来一段时间的血糖预测值。实例结果表明，该组合预测模型结合奇异点发现和处理算法能够显著提高预测能力和预测精度，很好地反应血糖上升或下降的趋势，具有很好的推广和应用价值。

［1］Ceriello A，Novials A，Ortega E，et al.Evidence that hyperglycemia after recovery from hypoglycemia worsens endothelial function and increases oxidative stress and inflammation in healthy control subjects and subjects with type 1diabetes［J］.Diabetes，2012，61 （11）：2993－2997.

［2］Georga E I，Protopappas V C，Polyzos D，et al.A predictive model of subcutaneous glucose concentration in type 1diabetes based on random forests ［C］//Engineering in Medicine and Biology Society.Annual International Conference of the IEEE，2012：2889－2892.

［3］Eren－Oruklu M，Cinar A，Quinn L，et al.Estimation of future glucose concentrations with subject－specific recursive linear models［J］.Diabetes Technology ＆ Therapeutics，2009，11（4）：243－253.

［4］Wang Z，Lai L，Xiong D，et al.Study on predicting method for acute hypotensive episodes based on wavelet transform and support vector machine［C］//3rd International Conference on Biomedical Engineering and Informatics.IEEE， 2010：1041－1045.

［5］Mo X，Wang Y，Wu X.Hypoglycemia prediction using extreme learning machine（ELM）and regularized ELM ［C］//Control and Decision Conference.IEEE，2013：4405－4409.

［6］Allam F，Nossair Z，Gomma H，et al.Prediction of subcutaneous glucose concentration for type－1diabetic patients using a feed forward neural network ［C］//International Conference on Computer Engineering ＆Systems.IEEE，2011：129－133.

［7］Pappada S M，Cameron B D，Rosman P M，et al.Neural network－based real－time prediction of glucose in patients with insulin－dependent diabetes［J］.Diabetes Technology ＆ Therapeutics，2011，13 （2）：135－141.

［8］Georga E I，Protopappas V C，Ardigo D，et al.Multivariate prediction of subcutaneous glucose concentration in type 1diabetes patients based on support vector regression ［J］.IEEE Journal of Biomedical and Health Informatics，2013，17 （1）：71－81.

［9］Facchinetti A，Sparacino G，Cobelli C.An Online SelfTunable Method to Denoise CGM Sensor Data ［J］.IEEE Trans Bio－Med Eng，2010，57 （3）：634－641.

［10］Ye R，Suganthan P N，Srikanth N，et al.A hybrid ARIMADENFIS method for wind speed forecasting ［C］//IEEE International Conference on Fuzzy Systems.IEEE，2013：1－6.

［11］Shumway R H，Stoffer D S.Time series analysis and its applications：With R examples［M］.Springer，2010.

［12］Box G E P，Jenkins G M，Reinsel G C.Time series analysis：Forecasting and control［M］.John Wiley ＆Sons，2013.