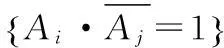基于BDD的小型核动力装置安全注射系统可靠性分析

【装备理论与装备技术】

基于BDD的小型核动力装置安全注射系统可靠性分析

时劭科1，陈力生1，陈玲1，杨宁2

(1.海军工程大学 核能科学与工程系， 武汉430033； 2.海司核安全部，海南 三亚572016)

摘要：小型核反应堆安全注射系统在运行过程中系统结构随时间的改变而变化，是具有明显阶段性的复杂任务系统；利用二元决策图(BDD)方法对该系统进行了可靠性分析，根据阶段代数的运算法则，采用基于最小相邻组件优先相邻排序方法，得到相应的二元决策图，根据相关失效数据得出安注系统完成任务的可靠度；结果表明：BDD方法能快速有效地分析多阶段任务系统可靠性，并能有效地缓解组合爆炸问题，使问题分析趋于简洁。

关键词：多阶段任务系统；二元决策图；安全注射系统；可靠性分析

收稿日期：2014-06-27

作者简介：时劭科(1989—)，男，硕士研究生，主要从事核科学与技术研究。

doi:10.11809/scbgxb2015.01.015

中图分类号：TL387

文章编号：1006-0707(2015)01-0052-05

本文引用格式：时劭科，陈力生，陈玲，等.基于BDD的小型核动力装置安全注射系统可靠性分析[J].四川兵工学报，2015(1):52-55.

Citation format:SHI Shao-ke，CHEN Li-sheng，CHEN Ling，et al.Reliability Analysis of Safety Injection System for Small Nuclear Power Plant Based on BDD[J].Journal of Sichuan Ordnance,2015(1):52-55.

Reliability Analysis of Safety Injection System for Small

Nuclear Power Plant Based on BDD

SHI Shao-ke1，CHEN Li-sheng1，CHEN Ling1，YANG Ning2

(1.Department of Nuclear Energy Science and Engineering, Naval University of Engineering,

PLA, Wuhan 430033, China; 2. Naval Nuclear Safety Department, Sanya 572016, China)

Abstract:The configuration of safety injection system in small nuclear reactor would transfer as time goes. This system is a complex mission system which has obvious phase. Binary decision diagram(BDD) was used to analysis the reliability of safety injection system in marine nuclear reactor. In the process of generating BDD, the rules of phase algebra and the method emphasizing the adjacency of neighbor variables’ ordering were used. Finally, the reliability of safety injection system in mission was calculated by failure data which was given in the paper. Result shows that PMS-BDD can give an efficient solution to the mission reliability of PMS and can avoid large basic events.

Key words: phased mission system; BDD; safety injection system; reliability analysis

多阶段任务系统(Phased Mission System，PMS)是指可以根据系统结构、成功准则、子系统的行为差异将系统的任务周期分成一系列连续不相交独立时间段的系统[1]。随着系统复杂性和自动化程度的提高，这类系统在实际工程应用中越发常见，小型核反应堆安全注射系统就是典型的一种。安全注射系统作为在一回路系统破裂引起失水事故后，向堆芯注水，保证淹没和冷却堆芯，防止堆芯熔化的系统，其可靠性在一定程度上决定了事故后堆芯的完整性，故对该系统进行可靠性评估是必要的。该系统在运行过程中呈现出明显的阶段特性，具体表现为在进行冷却堆芯的任务过程中，系统结构随时间(或触发信号)的变化而变化，因此，在对其进行可靠性分析时不能简单地将其看成单阶段系统，要考虑多阶段任务系统中各部件在不同阶段中的阶段相依性。

在众多的多阶段任务系统可靠性分析方法中，二元决策图(Binary Decision Diagram，BDD)方法能高效表示布尔函数且运算简捷，是PMS可靠性分析的重要方法[2]，故选用PMS-BDD方法作为分析反应堆安全注射系统可靠性的分析方法。

1PMS-BDD模型概述

1.1阶段代数运算法则

对于不可修系统的部件A，假设i、j代表不同的阶段，且i

Pr{Ai=1}-Pr{Aj=1}

1.2PMS中部件的失效函数

1.3PMS底事件排序

在生成对应的BDD过程中，PMS底事件的排序在很大程度上影响了最后产生的BDD节点数，因此，选用合适的PMS底事件排序方法对计算效率有很大影响。对PMS的底事件排序包括两个方面：系统各阶段之间的排序和系统底事件之间的排序。

1) 对于多阶段任务系统各阶段之间的排序方式，即同一底事件在不同阶段的基本变量之间的排序方式，Zang等[4]提出了两种方法：向前阶段依赖运算和向后阶段依赖运算。由于向后阶段依赖运算的排序方式在BDD的生成过程中能够自动删除一些冗余节点，生成较小的BDD规模，故本文对系统各阶段之间的排序选用此方法。

2) 对于系统底事件之间的排序，即整个任务中不同底事件间的排序方式，则采用王楠提出的基于最小相邻组件优先相邻排序[5]的方法。该方法已在文献[5]中得到论证，其对存在共同失效组件和共同失效模块的PMS进行分析时，优越性尤为明显。

2安全注射系统各阶段的系统结构

安全注射系统的功能[6]：在发生失水事故时能向堆芯提供足够的冷却水，保持堆芯的完整性，其原理图如图1所示。假设系统各部件都处于正常关闭状态，且不考虑喷淋系统，反应堆入口段出现破口，小型堆安注系统的各阶段响应如下。

第一阶段(0～t1时刻)：判断破口位置，隔离环路阶段。破口事件发生后，当稳压器压力降至某值x1时，安全注射系统投入使用。此时，由水源W1供水，控制阀A、D1、E开启，泵P1启用，控制阀D2开启，泵P2启用，开启控制阀I、K、L，冷却水经控制阀K、L同时注入堆芯。根据两条环路供水量的不同，迅速判断破口位置，相应地关闭控制阀K，冷却水仅从控制阀L注入堆芯。

在该阶段中，由于判断破口位置所用时间相比于该阶段的任务时间短很多，因此，假设从安全注射系统投入到关闭阀K所用时间可以忽略不计，即从阶段开始到结束冷却水仅从阀L注入堆芯。相应故障树图2中Phase1所示。

第二阶段(t1～t2时刻)：淹没堆芯阶段。当稳压器压力继续下降至低于某值x2(x2

第三阶段(t2～t3时刻)：再循环冷却阶段。根据总注射水量限制和堆舱高水位报警，停止水源W1和水源W2的供水，关闭控制阀B、D1，停运泵P1，打开阀C，水源W3经过滤器F向泵P2供水，关闭控制阀I，打开阀J，冷却水经热交换器HE冷却，通过阀L注入堆芯。相应故障树如图2中Phase3所示。

图1　安全注射系统原理

图2　安全注射系统各阶段故障树

3生成BDD及计算分析

3.1相应BDD的生成

1) 对 PMS故障树进行化简。从表2中所给各部件的失效数据可知，水源的运行失效率为0，故可将其从故障树中删去。在PMS中存在共同失效组件L、H、P2、I，则删去Phase1和Phase2中的L、H、P2，以及Phase1中的I。对PMS故障树重新整理，则得到新的PMS故障树，如图3所示。

图3　化简后的故障树

2) 对图3所示PMS故障树进行遍历，得到如表1的系统各部件的遍历结果。

表1　各部件遍历结果

3) 按照文献[5]中所介绍的方法对安全注射系统中的部件进行排序。共同失效组件给予最高优先级，组件出现的阶段数越大给予的优先级越高，若同一阶段中存在多个共同失效组件，则按从左到右的顺序进行排序，得到其排序为P2

P2

从而得到最终的PMS底事件排序：

P23

A1

4) 按照得到的底事件排序结果，构造对应的BDD，得到该系统的PMS-BDD如图4所示。

图4　安全注射系统的PMS-BDD

3.2实例计算

在对小型核反应堆安全注射系统进行可靠性分析时，做出如下假设：

该系统是不可修的；系统中各个组件之间是功能独立的，即每个部件的状态(工作或失效)都不影响其他部件；任务中任何一个阶段的失效只取决于各部件失效的组合模式，与部件失效的先后顺序无关；系统是单调的，即系统中每个部件的状态(工作或失效)都会对系统造成影响，并且系统的状态不会因为某个组件的失效而变得更好。各部件故障率[7]在表2中列出。

根据生成的PMS-BDD(图4)，得到系统可靠度为：

R=P(P23·H3·L3·I2·F3·C3·J3·HE3·

B2·A1·D21)+P(P23·H3·L3·I2·F3·

E2·G2)+P(P23·H3·L3·I2·F3·C3·

假设系统中各部件的初始成功概率为1，寿命均服从指数分布，各阶段起始时间采用文献[6]中所提供的时间节点，分别为t1=50 min，t2=2 h，t3=5 h。通过上述数据，计算可得各部件在各阶段的可靠度，代入上式可得R=0.993 6。

表2　各部件失效数据

3.3计算结果分析

对各部件进行结构重要度分析[8]，分别计算得到各部件重要度如下表3所示。PMS中各部件的结构重要度计算与传统故障树的计算有一定差别，同一部件在不同阶段形成不同的基本事件在PMS-BDD中占有不同的位置，因此，在对其进行结构重要度分析时，需要对其进行合并，以控制阀A为例进行说明。控制阀A的结构重要度为

其中，A1、A2为控制阀A由于运行阶段的不同分为的两个基本事件，在PMS-BDD中占据不同位置。

表3　各部件结构重要度

从计算结果可知，小型核反应堆安全注射系统的可靠性较高，满足失水事故下保持堆芯完整性的功能需求。部件P2、H、L、I、F、C、J、HE、A的重要度最高，从生成的PMS-BDD中也可发现，在任务第三阶段，部件P2、H、L、F、C、J、HE串联运行，导致单个部件的可靠性对完成阶段任务的影响较大，其中泵P2占据了PMS-BDD的最高层，这是由于该泵需在3个阶段都正常工作，任何阶段的故障都将直接或间接导致整个任务的失败。

4结论

本文应用BDD方法对小型核反应堆安全注射系统进行了可靠性分析，结果表明泵P2、过滤器F、换热器HE、止回阀H、控制阀A、C、I、J、L的可靠性对系统完成指定任务具有较大影响，应加强日常监测，及时更换性能退化的部件以保证航行安全及安全注射系统的高可靠性，且可改进关键部件的设计以提高系统整体可靠性。另外，通过对比各部件的优先级排序和结构重要度发现两者排序基本一致，具有较高优先级的部件其结构重要度也较大，因此，可通过生成的PMS-BDD粗略地估计各部件的结构重要度大小。

从分析过程中可知，PMS-BDD方法建模简单，有效降低了计算的复杂性，同时，也避免了传统故障树分析中所存在的组合爆炸问题，故可将该方法引入到对小型核反应堆其他系统的可靠性评估中。

参考文献：

[1]ESARYJD,ZIEHMSH.Reliabilityanalysisofphasedmissions[J].ProceedingsofReliabilityandFaultTreeAnalysis，1975，27：213-236.

[2]AKERSSB.Binarydecisiondiagram[J].IEEETransactionandComputers，1978，C-27(6)：509-516.

[3]SOMANIAK,TRIVEDIKS.Phased-missionsystemanalysisusingbooleanalgebraicmethods[J].PerformanceEvaluationReview:Proc.ACMSIGMETRICSConf，1994，22(1)：98-107.

[4]ZANGXY,SUNHR,TRIVEDIKS.ABDD-basedalgorithmforreliabilityanalysisofphased-missionsystems[J].IEEETransactionsonReliability，1999，48(1)：50-60.

[5]王楠，杜素果.一种多阶段任务系统的BDD排序新方法[J].科学技术与工程，2010，17(10)：4217-4224.

[6]陈玲，尚彦龙，蔡琦，等.LOCA事故下安全注射系统可靠性的GO-FLOW法分析[J].原子能科学技术，2012，46：324-329.

[7]阎凤文.设备故障和人误数据分析评价方法[M].北京：原子能出版社，1988.

[8]徐亨成，张建国.基于BDD技术下的故障树重要度分析[J].电子机械工程，2003，19(6)：1-4.

(责任编辑周江川)