基于神经网络的弹道修正弹落点预测方法

【装备理论与装备技术】

基于神经网络的弹道修正弹落点预测方法

曹红锦1，常思江2

(1.中国兵器工业 第五九研究所，重庆400039； 2.南京理工大学 动力工程学院，南京210094)

摘要：为了分析神经网络运用于弹道预测的可行性，构建了实用的弹道预测工具，建立了基于神经网络理论的弹道预测模型。利用二自由度质点弹道模型，选取BP网络和Elman网络进行神经网络弹道预测仿真。基于误差反向传播理论，比较了带动量项算法与自适应学习率算法这2种网络权值训练速度。对2种网络不同隐层节点数的学习误差和预测误差进行了对比分析。数值仿真计算结果表明，神经网络具有较高的预测精度，36.7 km射程仅有不足100 m的射程误差，12.3 km射高仅有不足70 m的高度误差，预测结果满足要求，利用神经网络进行弹道预测是合理可行的。

关键词：弹道预测；神经网络；误差反传；数值仿真

收稿日期：2014-08-12

作者简介：曹红锦(1977—)，女，高级工程师，主要从事科技情报研究。

doi:10.11809/scbgxb2015.01.005

中图分类号：TJ303.4

文章编号：1006-0707(2015)01-0017-05

本文引用格式：曹红锦，常思江.基于神经网络的弹道修正弹落点预测方法[J].四川兵工学报，2015(1):17-20.

Citationformat:CAOHong-jin,CHANGSi-jiang.StudyonProjectilesImpactPointPredictionMethodforTrajectoryCorrectionBasedonNeuralNetwork[J].JournalofSichuanOrdnance,2015(1):17-20.

StudyonProjectilesImpactPointPredictionMethodfor

TrajectoryCorrectionBasedonNeuralNetwork

CAOHong-jin1, CHANG Si-jiang2

(1.No. 59InstituteofChinaOrdnanceIndustries,Chongqing400039,China;

2.SchoolofEnergyandPowerEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

Abstract:In order to discuss the feasibility of neural network uses for trajectory prediction, and to create a practical prediction trajectory tool, we built a trajectory predictive model based on neural network. It used two degrees of freedom particle trajectory model to do neural network trajectory prediction simulation by selected BP network and Elman network. Based error back propagation theory, it compared two types of weight training velocities from momentum back propagation and adaptive learning rate back propagation in the network structures, and the comparative analysis of the learning error and prediction error of the two networks in different amount of hidden nodes were discussed. Numerical results show that it is less than 100m range error of 36.7 km and less than 70 m height error of 12.3 km shot high. The neural network has high prediction accuracy, and its trajectory prediction results meet the requirements. The ballistic prediction using neural networks is reasonably practicable.

Keywords:ballisticprediction;neuralnetwork;errorbackpropagation;numericalsimulation

弹道修正弹就是在制式炮射弹药加装弹道修正模块以提高炮弹的射击精度。弹道探测技术、弹道解算技术、控制执行机构是弹道修正弹3大关键技术[1-3]。只有精确预测了落点，才能推算出修正执行机构动作时间、工作时长等重要信息，最终使弹丸命中目标。如果弹道预测不能很好完成，将严重影响弹道修正弹的射击精度。

目前，国内外已提出了一些落点预测方法[4-6]，但这些预测方法往往需要大量的迭代运算，计算量较大，现阶段弹载计算机的运算能力很难满足要求，而神经网络[7-9]为此提供了新的解决办法。训练好的神经网络运算量很少，现有弹载计算机完全可以胜任。神经网络在弹道预测中的应用很好地解决了实时跟踪和高精度预测的问题，该算法的引入从多方面提高了现有弹载计算机弹道预测的能力，使弹道预测的作用发挥得更加完善。

1基于神经网络的预测模型

1.1弹道预测用动力学模型

采用外弹道基本假设条件下的弹丸质心运动方程组，以时间t为自变量，采用直角坐标形式和43年阻力定律，可得：

(1)

(2)

运动学关系如下：

(3)

(4)

关联方程

(5)

式中：x,y分别为距离和高度；u,w分别为距离和高度方向上的速度分量；c为弹道系数；π(y)为气压函数；K(vτ)为阻力函数；θ为弹道倾角；g为重力加速度；τ为虚温；τon为地面标准虚温。

上述4个方程有4个未知数，方程组封闭。联立式(1)～式(4)即可求解。

1.2BP神经网络算法

BP算法的基本思想是，学习过程由信号的正向传播与误差的反向传播2个过程组成。输入信号由输入层传入，经过隐层处理，由输出层输出。若输出信号与期望输出(即导师信号)不相符，则生成误差信号，并经由网络反向传递。误差反传是误差信号以某种形式通过隐层向输入层传递，并将误差信号根据一定计算方式平摊给各层所有节点，以获得各节点的误差信号，此信号即是各节点权值修正的依据。由输入信号计算出输出信号，然后获取误差信号，再进行权值调整，这个流程就是神经网络的一次学习过程。通过不断重复这个学习过程，使网络的输出误差减小到可接受范围，或者是完成预定的学习次数，便认为神经网络已完成学习。

1.3标准BP算法及其改进

在标准算法上进行一些改进，可以提高BP网络的适应性及应用能力。本文针对学习中出现振荡、平坦区域学习缓慢这2个方面采用了2种改进算法：带动量项标准算法与带动量项自适应学习率算法。

1.3.1带动量项标准算法

标准BP算法在调整权值矩阵时，只按t时刻误差梯度下降方向调整，没有考虑之前时刻的梯度方向，从而导致训练过程振荡，收敛缓慢。因此，在权值调整公式中增加一动量项。其表达式为

ΔW(t)=ηδX+αΔW(t-1)

(6)

可以发现，增加的动量项即从前次权值调整量中取出部分叠加至本次调整中，α为动量系数，一般由α∈(0,1)。动量项反映了对调整经验的积累，对于当前调整起到一定阻尼作用。

1.3.2自适应学习率算法

在标准算法中，学习率η为常数，但在实际应用中，如同网络结构的选择一样，很难确定一个始终适合的最佳学习率。过小的η使得训练在误差曲面平坦处进行缓慢，而η过大可能会使训练在误差变化剧烈区域跨过较窄的“凹坑”，导致训练出现振荡。如果学习率可以在训练过程中进行适应性更改，便可以很好地解决这些问题。

本文所采用的自适应学习率算法在权值调整中仍然加入动量项，并对上述2种算法的学习效果进行对比。

1.4Elman网络

动态网络必须在网络中引入短时记忆功能，可以通过2种方式进行，一种是通过演示单元储存以前的输入状态，另一种则是引入反馈是网络成为动态系统。Elman网络便属于后者。

Elman网络可以采用静态BP算法来使计算较为简便。但作为动态网络，Elman网络的输出不仅与当前时刻输入有关，还与过去时刻的输入有关，因此对于精确计算应采用动态学习规则。对于BP网络的学习算法推倒采用了链式法则的算法，而在Elman网络中，一般采用有序链式法则的算法。

2算例仿真与分析

本文就2种神经网络的不同算法和不同节点数分别进行算例仿真，前面提到的弹丸动力学模型将用于生成训练数据。

2.1BP网络弹道预测模型

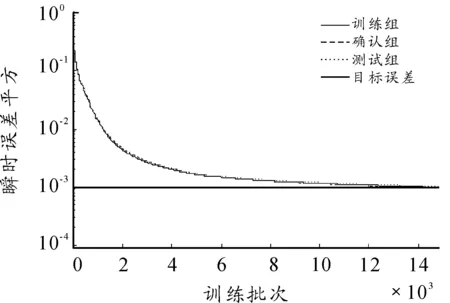
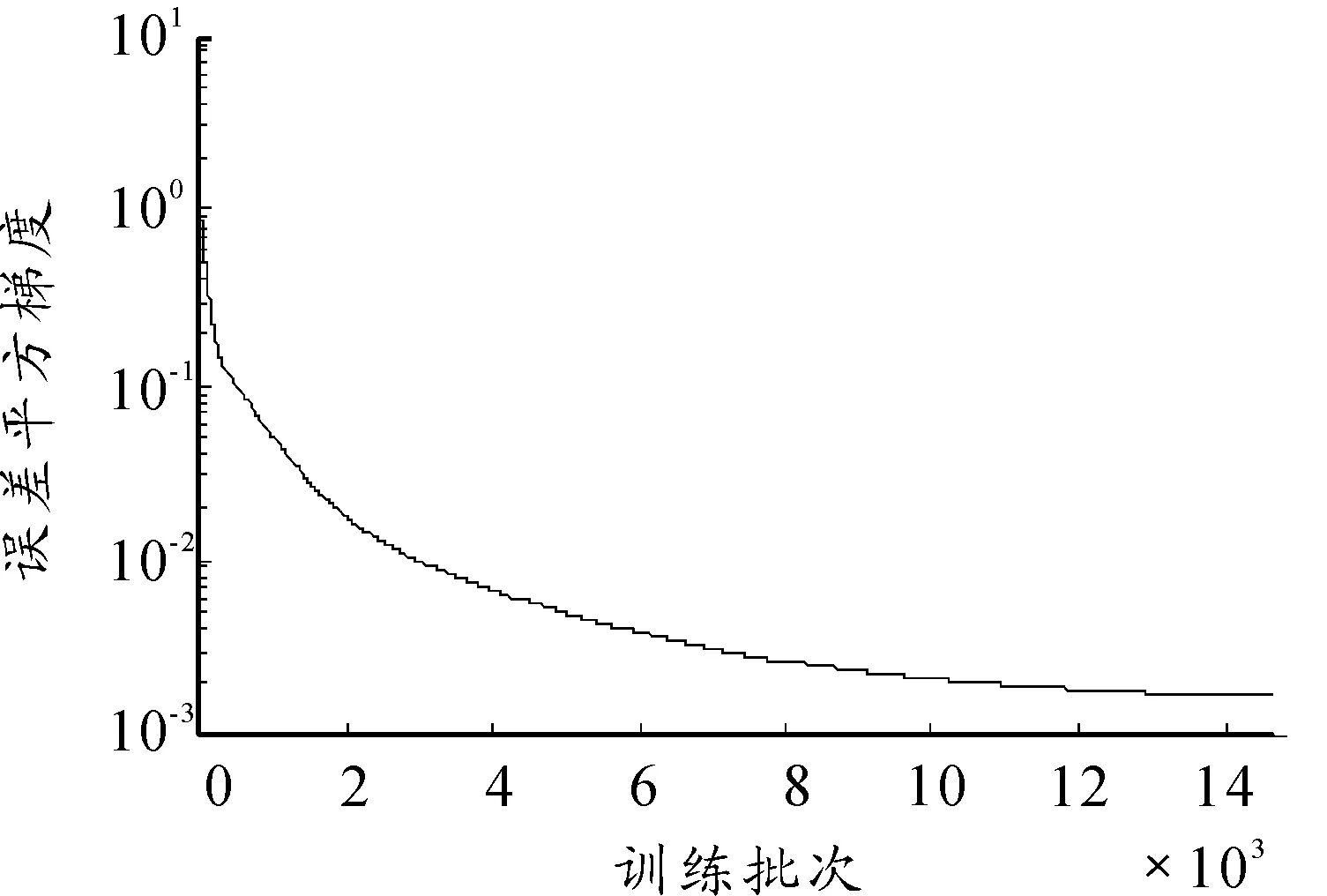
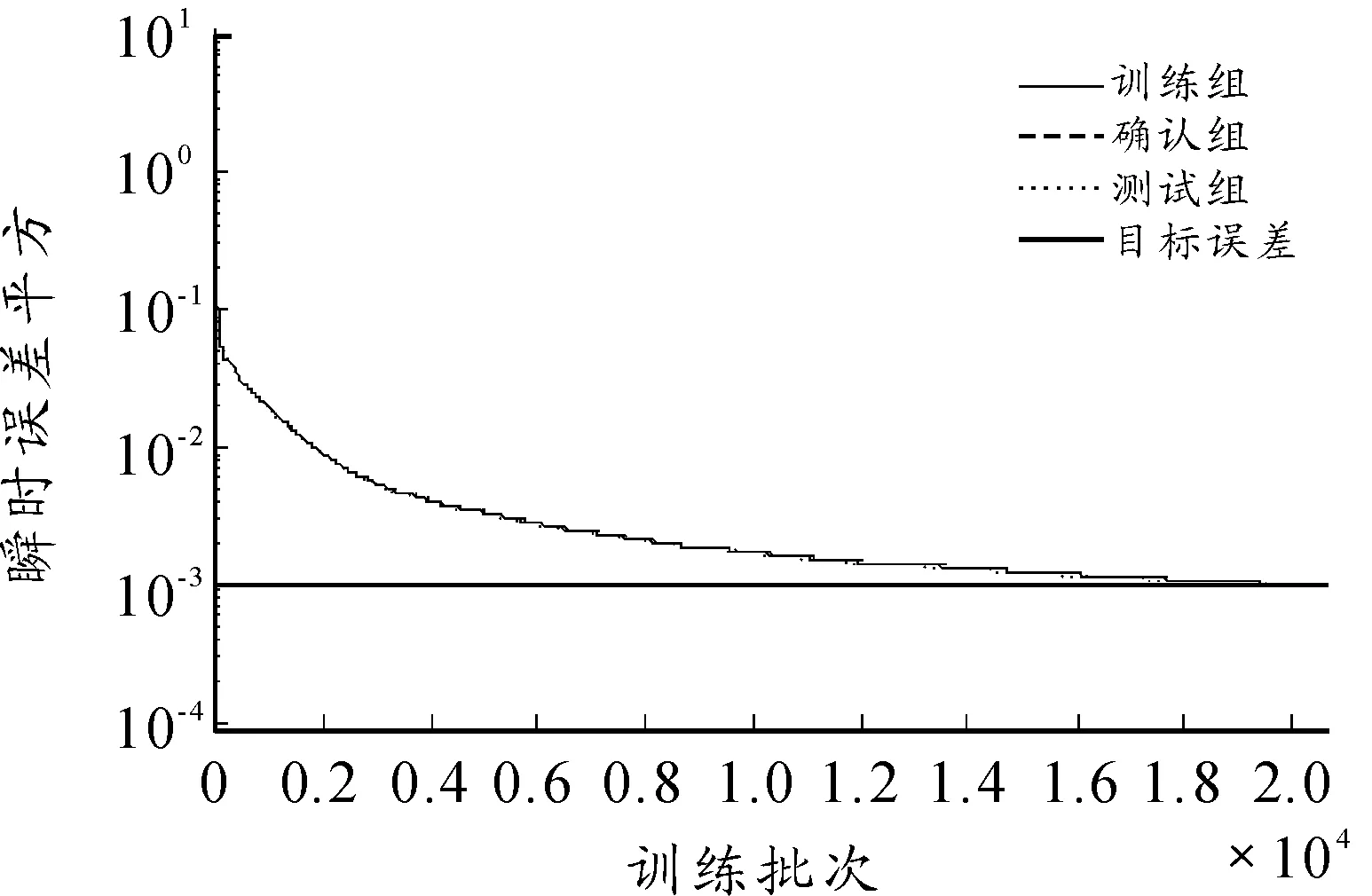
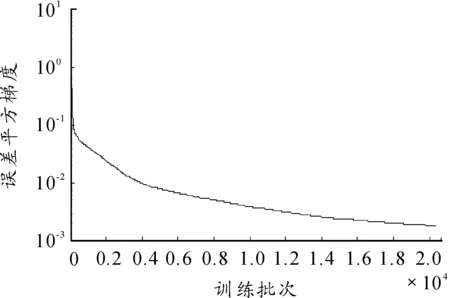
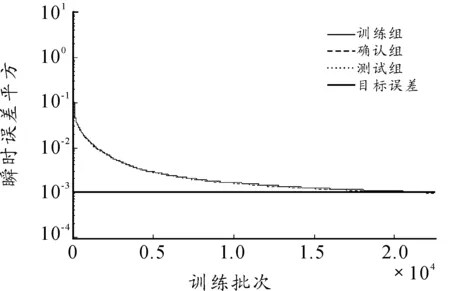
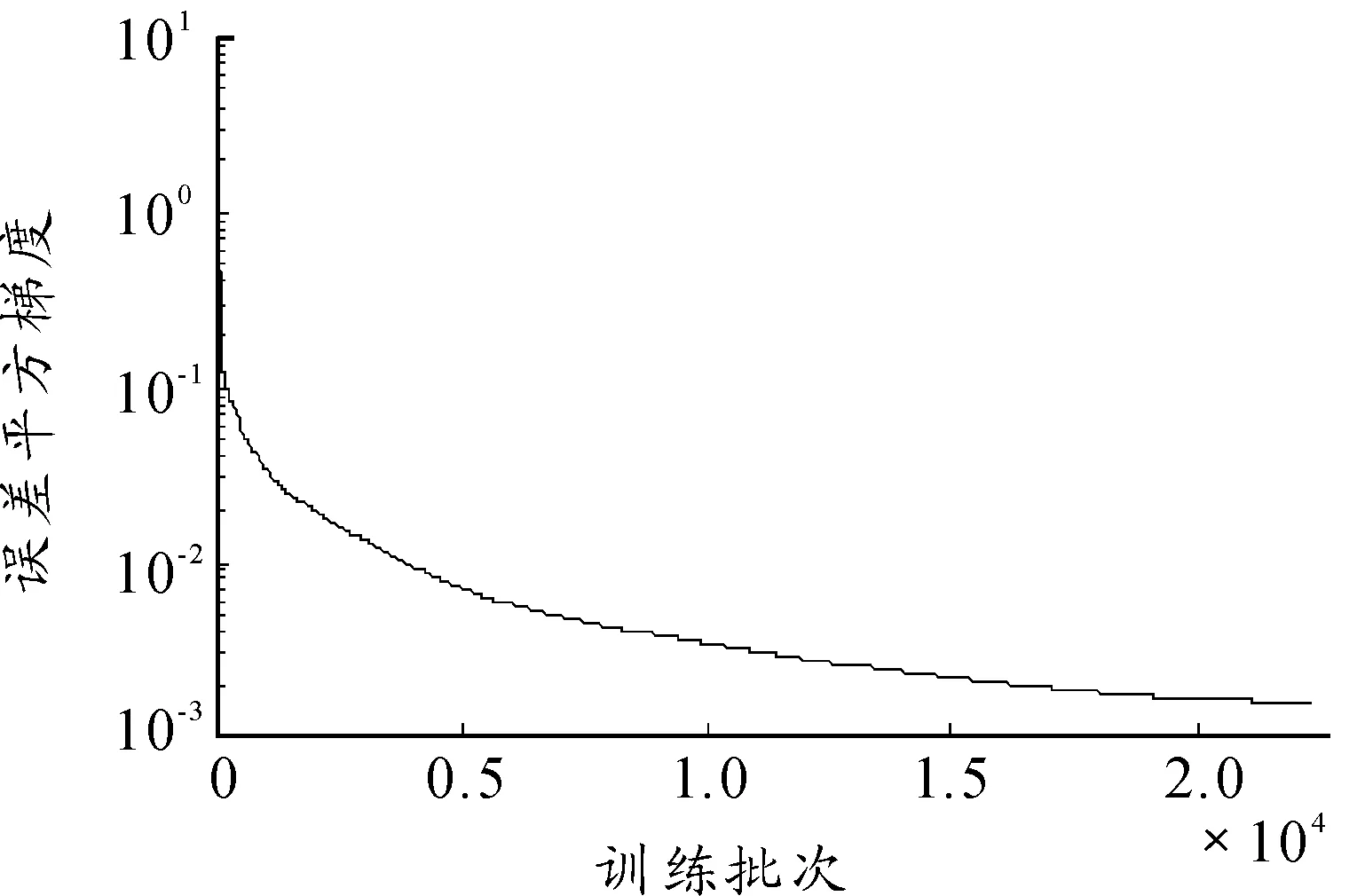
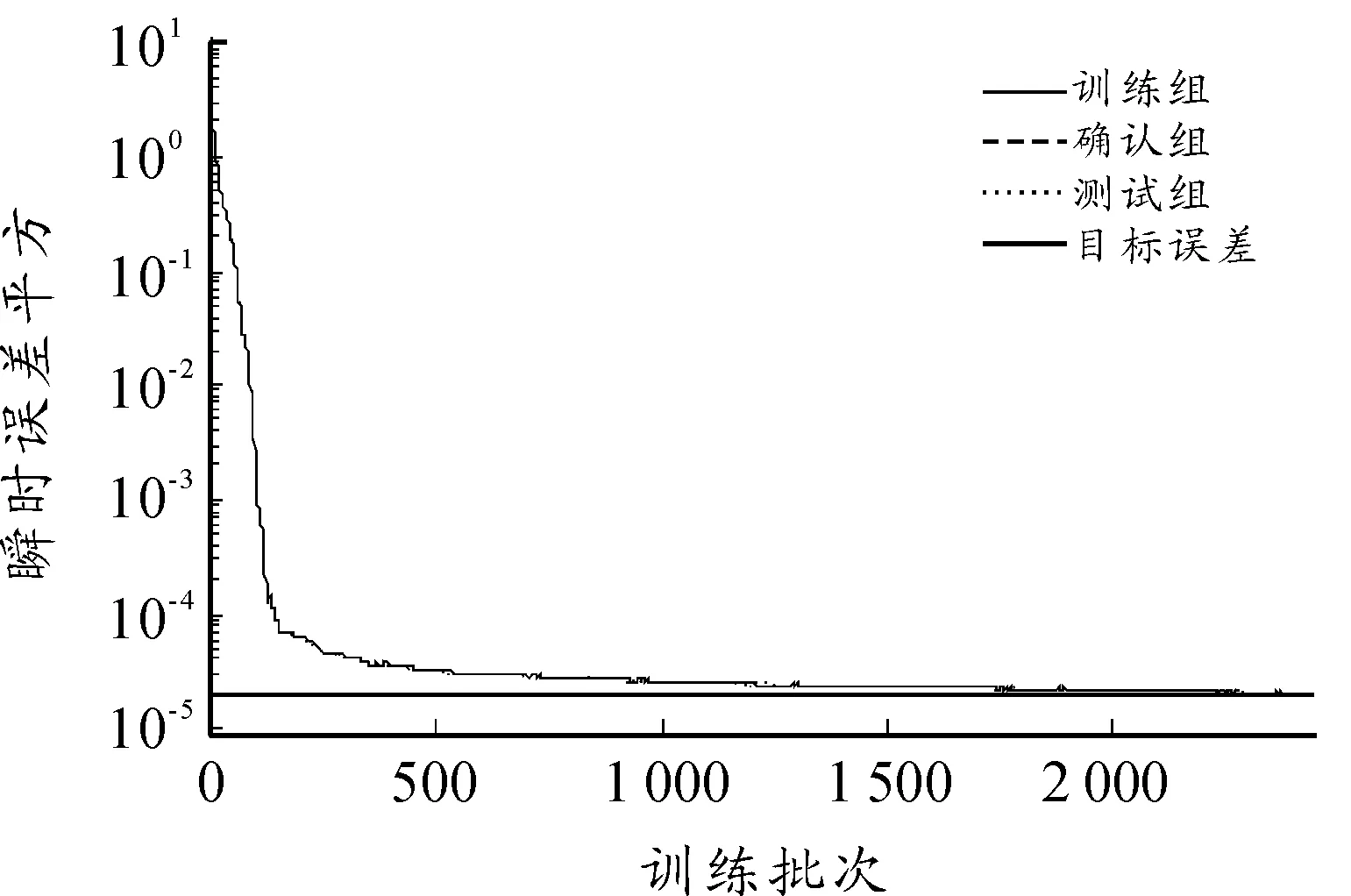
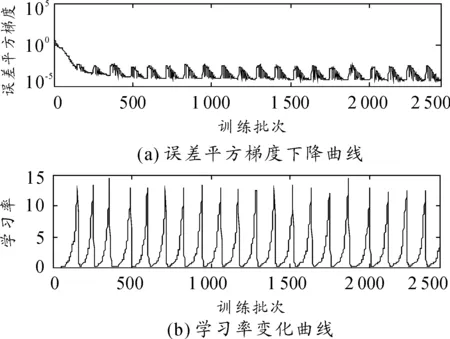
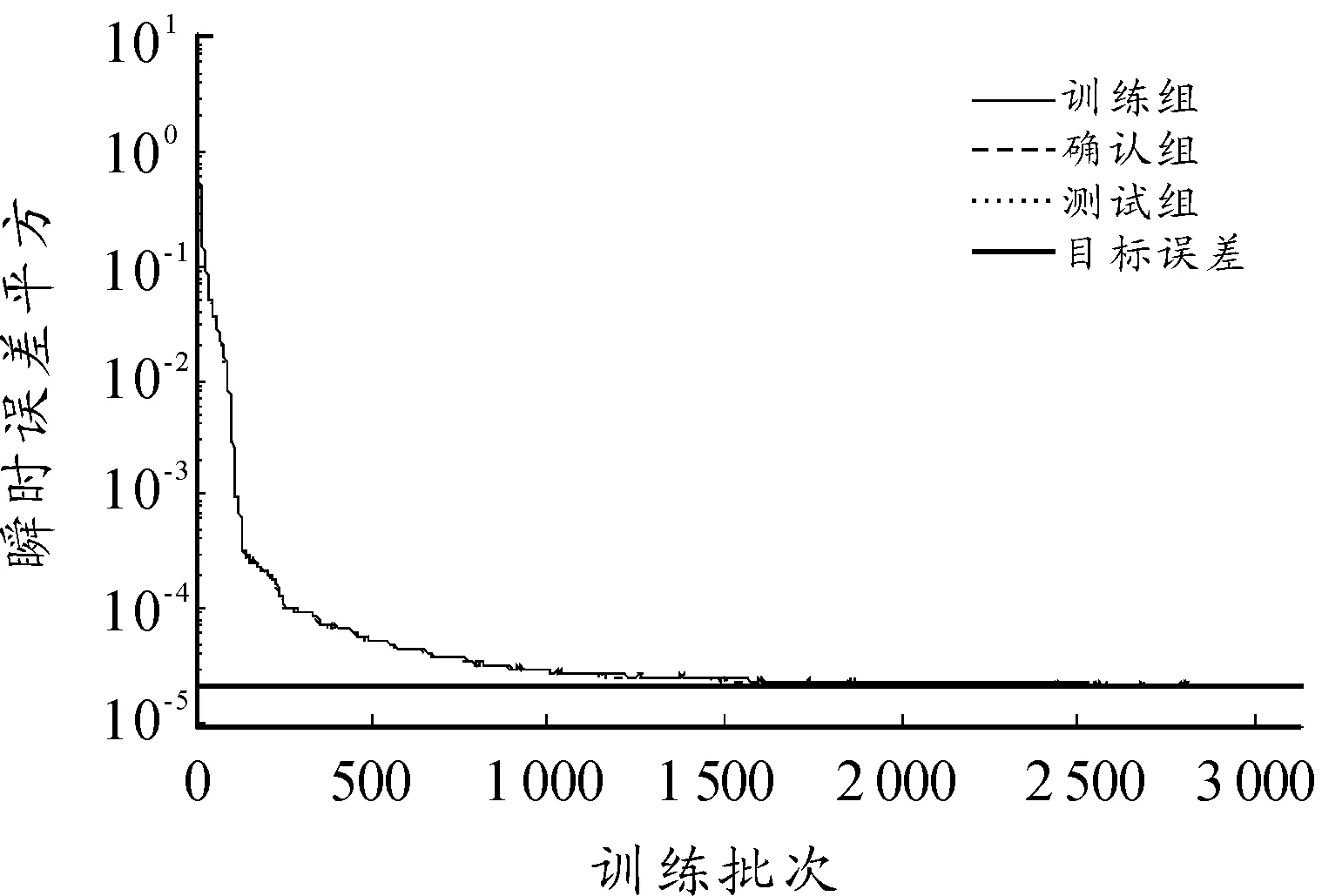
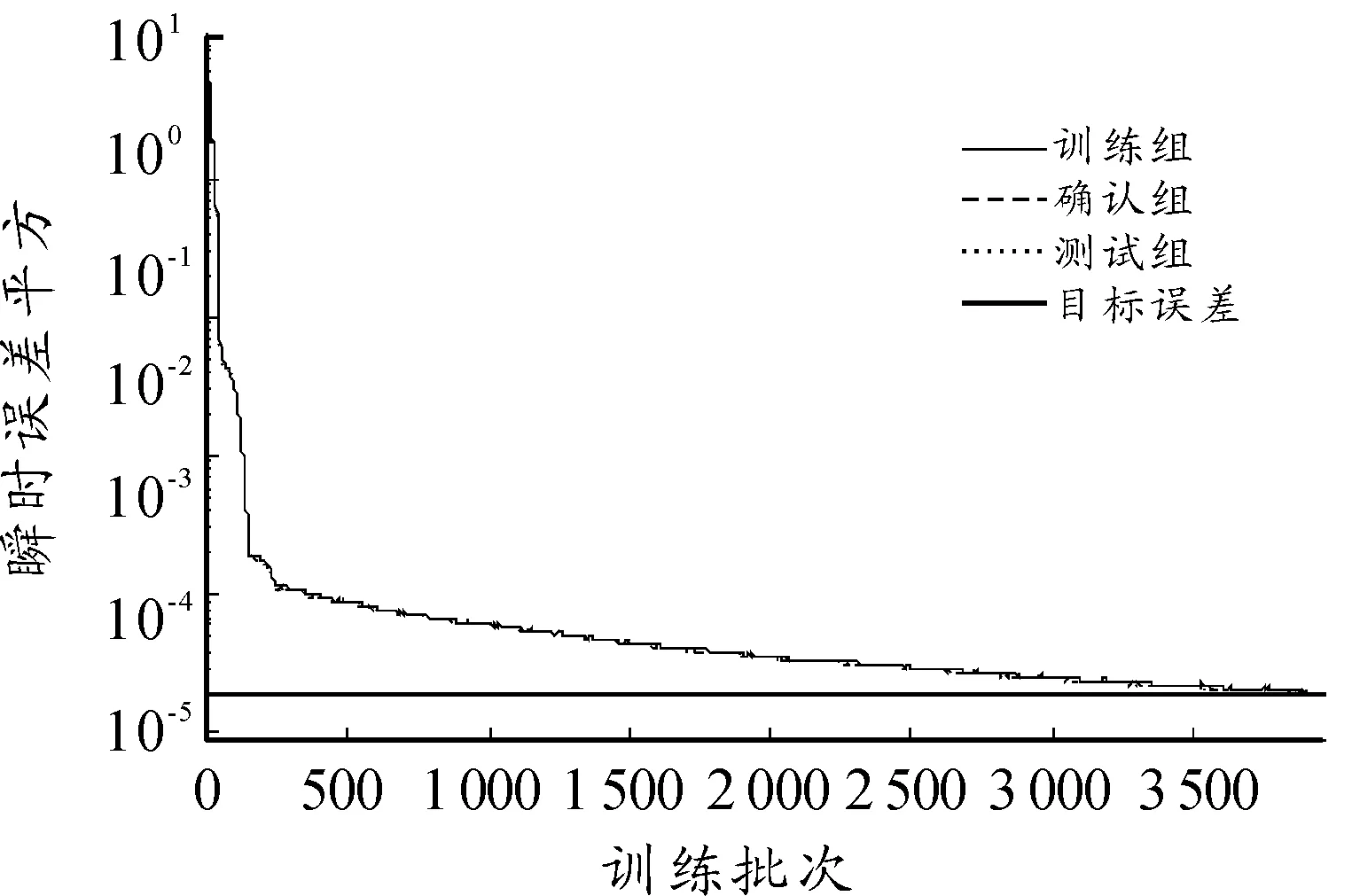
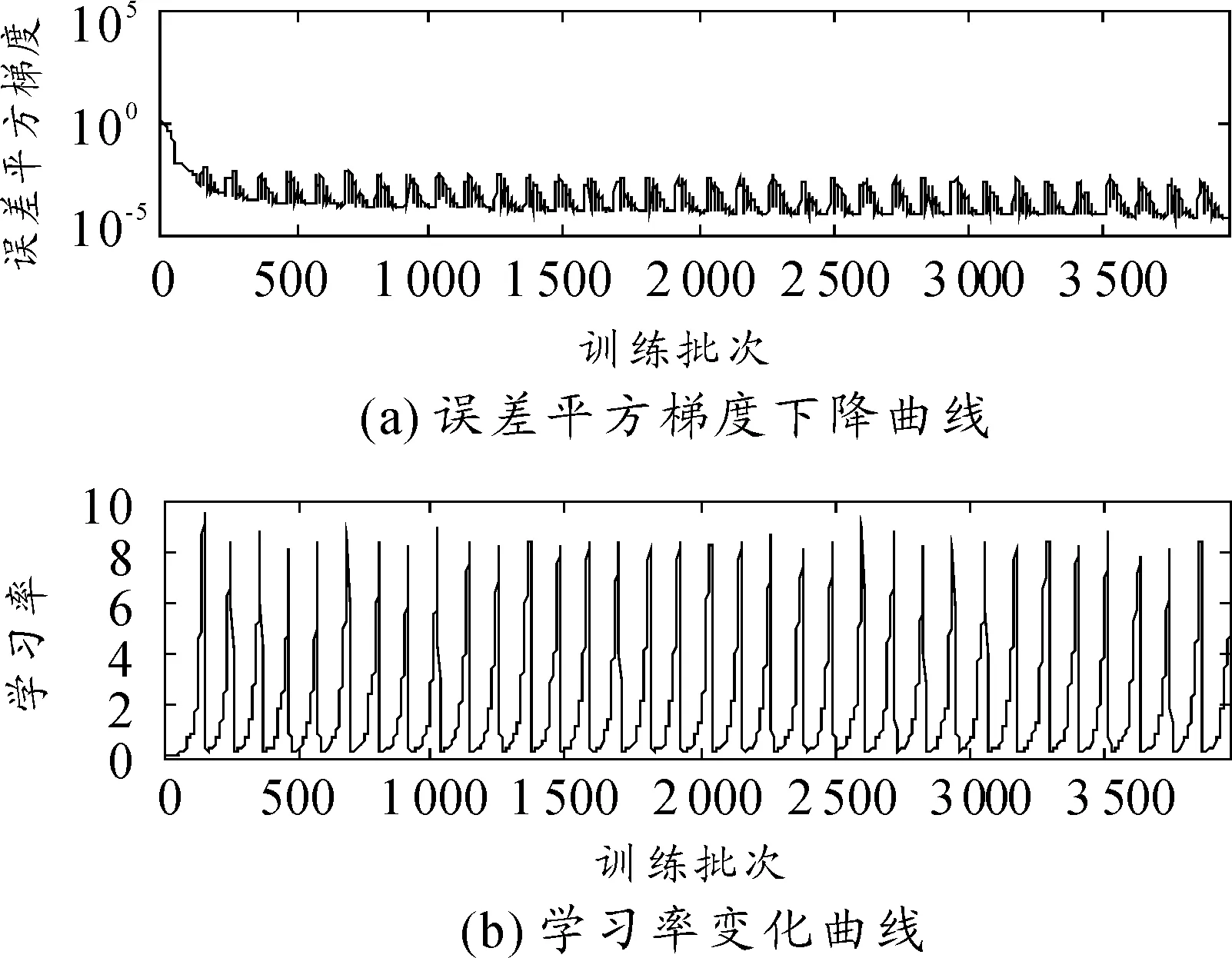
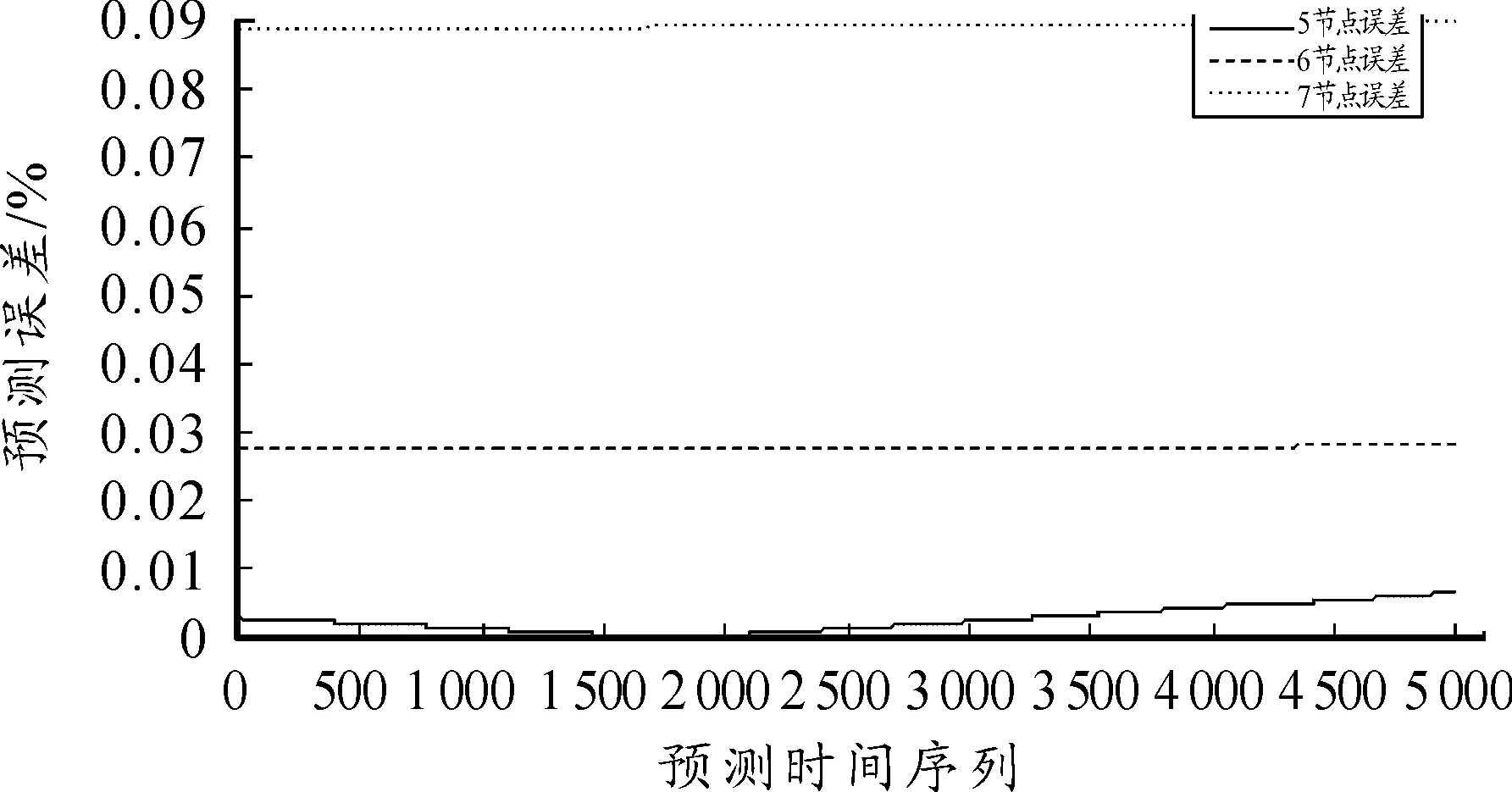
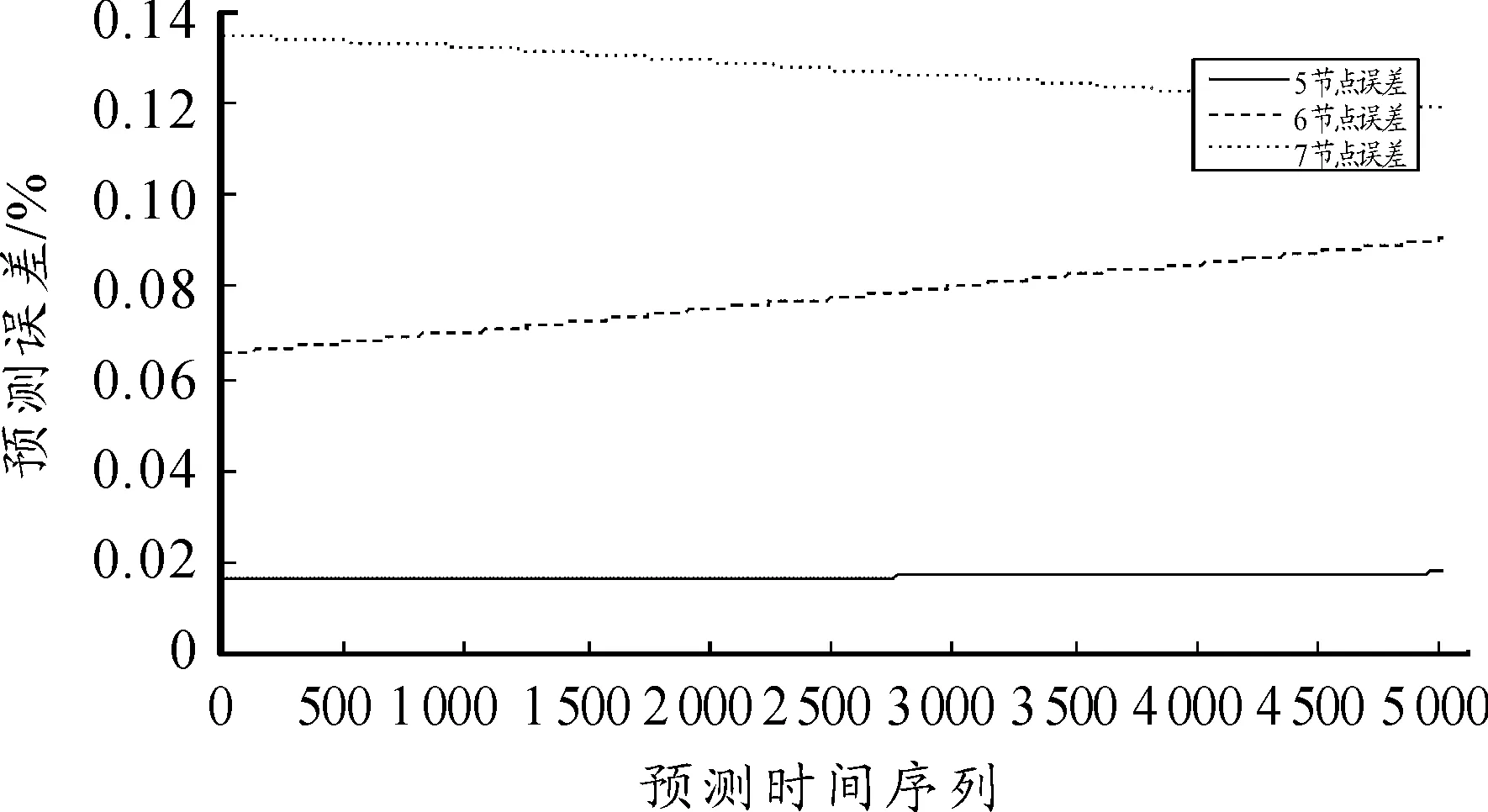
本文模拟了5个、6个和7个隐层节点数的3种不同神经网络，网络训练结果如图1～图8所示。图1～图6依次显示了隐层节点数由5个变化至7个时，网络学习过程中瞬时误差平方与误差平方梯度变化的情况。瞬时误差平方曲线与误差梯度下降曲线纵轴均采用对数坐标轴，下文亦同。图7与图8显示了3个网络进行弹道预测的误差情况。计算参数如下：弹丸初速为1 000m/s，扰动初速为995m/s，射角为45°，学习率为0.01，动量参数为0.9，学习终止条件为E

仿真结果如下：

网络1：隐层节点数为5，仿真结果如图1、图2所示。

图1　节点网络误差下降曲线

图2　节点误差梯度下降曲线

网络2：隐层节点数为6，仿真结果如图3、图4所示。

图3　节点网络误差下降曲线

图4　节点误差梯度下降曲线

网络3：隐层节点数为7，仿真结果如图5、图6所示。

由图1，图3，图5可以看到，网络初始权值的随机性虽然导致其实误差平方各不相同，但网络几乎都可以在开始很少的训练批次内使误差平方下降到10-1这个数量级。当误差梯度逐渐减小至几乎不发生变化时，可以判断到达了误差曲面的平坦区域，进入了误差极小点区域。但是否为全局极小无法判断，这也是BP算法的缺陷。

由图7与图8可以看出，神经网络进行弹道预测有着很高精度。3个网络在射程与高度上的预测误差都基本在0.5%范围内。但不同节点数之间预测误差差异较大，6节点显然是比较合适的隐层节点数。节点过少可能使网络不具有足够复杂程度学习样本规律，不能很好地预测。而过度复杂的网络则出现过度学习而降低了泛化能力，使得网络外推的能力下降，导致误差增大。

图5　节点网络误差下降曲线

图6　节点误差梯度下降曲线

图7　x方向网络预测误差

图8　y方向网络预测误差

2.2Elman网络弹道预测模型

Elman网络采用算法与BP算法类似，基本思想依然是误差反传。本节讨论了自适应学习率情况下网络的训练情况，仿真条件与前文所述相同。

本节采用自适应学习率算法进行Elman网络训练，对隐层节点数由5增至7时3种不同网络结构的仿真模拟。图9～14依然是不同节点数网络的瞬时误差平方下降曲线与误差梯度下降曲线，图15和图16对3个网络预测结果进行对比。

仿真结果如下：

网络1：隐层节点数为5，仿真结果如图9、图10所示。

图9　5节点网络误差下降曲线

图10　5节点误差梯度下降曲线

网络2：隐层节点数为6，仿真结果如图11、图12所示。

网络3：隐层节点数为7，仿真结果如图13、图14所示。

由图9、图11和图13可以看到，网络误差平方下降趋势依然是不断振荡中快速到达较小水平，是明显的自适应学习率算法的特征。同时可以看到，误差平方曲线在由快速下降向平缓下降的转折过程越来越误差梯度变化与学习率变化间的关系也与前文所述相同，出现此消彼长的状态。

图15与图16显示了网络最终的预测精度，可以看出，使用自适应学习率算法的Elman网络基本达到了本文所有仿真网络误差的最低水平。特别是5节点网络，其x方向的误差最大不足0.066%，几乎可以认为是准确预测。而其他节点数网络x、y 2个方向上的预测误差几乎都在0.1%以内，仅7节点网络在y方向上的误差为1.2%～1.4%。

图11　6节点网络误差下降曲线

图12　6节点误差梯度下降曲线

图13　7节点网络误差下降曲线

图14　7节点误差梯度下降曲线

图15　x方向网络预测误差

图16　y方向网络预测误差

3结论

本文对不同神经网络在弹道预测中的应用进行了数值研究，得到以下主要结论：

计算结果表明：坝基轻壤土（或砂壤土）在地震烈度7度时，就有开始破坏的可能性，在8度及其以上时地表下砂壤土全部液化及地表下10 m范围内中细砂层开始液化。饱和轻壤土（或砂壤土）抗震稳定性最差，是引起地基液化破坏的主要土层。

1) 使用神经网络进行弹道预测是可行的，而且具较高的计算精度。

2) 自适应学习率算法能够在相同条件下使网络训练获得更高的预测精度，有较高的实用价值。

3)Elman网络相较于BP网络的预测能力更好，动态系统应利用动态网络建模以更好地反映系统内在规律。

以上研究结果为神经网络在弹道预测中的实际工程应用提供了理论基础。

参考文献：

[1]张成.脉冲修正弹药射程预测控制方法[J].弹道学报,2010,22(1):19-23.

[2]王中原,史金光,李铁鹏.弹道修正中的控制算法[J].弹道学报,2011,23(2):19-21,27.

[3]张民权,刘东方,王冬梅,等.弹道修正弹发展综述[J].兵工学报,2010,31(S2):127-130.

[4]史金光,徐明友,王中原,等.卡尔曼滤波在弹道修正弹落点推算中的应用[J].弹道学报,2008,20(3):41-43.

[6]陈映,文树梁,程臻.一种基于多模型算法的纯弹道式弹道落点预报方法[J].宇航学报,2010,31(7):1825-1831.

[7]陈烺中,樊蓉,王冠男,等.TBM末端机动弹道预测[J].电光与控制,2006,13(4):9-12.

[8]WoosungPark,Chang-KyungRyoo,ByoungSooKim,etal.ANewPracticalGuidanceLawforaGuidedProjectile[C]//AIAAguidance,navigation,andcontrolconference,2011.2011(1):826-834.

[9]史忠植.神经网络[M].北京:高等教育出版社,2009.

(责任编辑周江川)