一个新的时滞线性系统稳定的充分必要条件
张怡林,朱育志,刘士亚
(1.广东焕泰电力建设有限公司,广东佛山528000;2.广东立胜电力设备公司,广东佛山528000;3.佛山科学技术学院自动化系,广东佛山528000)
时滞现象在物理和生物系统中及实际生产生活中广泛存在,如系统信号的量测(特别是复杂的在线分析仪)、长管道进料或皮带传输、缓慢的化学反应过程等,也常见于电路、光学、神经网络、生物环境、数据网络及冶金工业、建筑结构、机械传动等领域。由于应用背景广泛,一直深受众多研究者的关注[1-2]。时滞系统分析方法主要有2类,1)特征方程根在复平面上位置的判断[3-4];2)基于计算机数值分析工具的Lyapunov稳定性分析法[5-6]。对于一维时滞系统,还可以应用Lambert方程分析[3]。
本文针对一维时滞线性系统,采用基于复变函数的几何方法,研究其稳定条件。所给出的结论是充分必要条件,不存在任何保守性。文献[4]也给出了一个充分必要条件,与之比较,本文结论有2个方面的改进:1)证明过程简洁;2)结论简明,给出的表达式不需要试算和验算,是直接的结果。文末给出的数值例子证明了该方法的有效性,并与相关研究结果进行了比较。
1 标量时滞系统稳定的充要条件
1.1 时滞无关稳定性
考虑标量时滞系统稳定性

式(1)中,x(t)(t≥0)为系统的状态;a,b∈R 为实常数;h≥τi>0(i=1,2…,∞),τi为系统的时滞,h 为系统可能的最大时滞。设系统(1)在t∈[-h,0]的状态是确定的(可以是未知的)。
引理 1[5]设 F(jω)=jω-a-b e-jτω,标量时滞系统(1)稳定的充要条件是

令 θ=ωτ,则(2)式可改写为

于是有

因此,引理1成立等价于
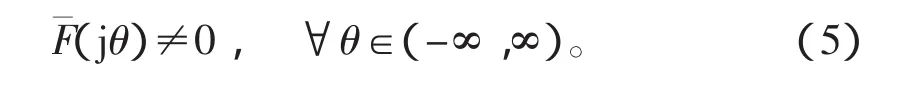
定义圆C:z=e-jθ,则引理1等价于L1与C在复平面上无交点,如图1所示。
定理1 设a<0,系统(1)全时滞稳定的充要条件是

证明 下面分别证明充分性和必要性。
证明 设直线L与圆C的交点为P(x,j y),有


图1 复平面上的直线与单位圆
从图1可以看出,L1位于单位圆之外。由引理1知,系统稳定。
下面两种情况值得注意,特此作如下说明。
(1)Hale[4]给出了结论需要首先假定一个值,然后用假定值去解一个方程,再验算2个不等式,如果不满足,则再假定,重复至满意的结果为止。
(2)文献[3]的结果可用MATLAB平台提供的函数lambertw()计算,同样需要先假定后验算,而本文结果是直接得到的。
1.2 实例
例1考虑下列系统的稳定性
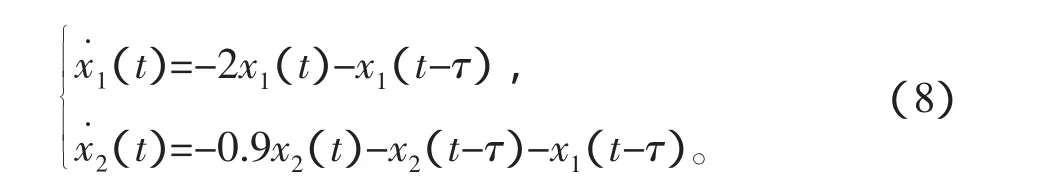
证明 相关研究成果如表1所示。由定理1知,子系统x1(t)是全时滞稳定的,可知 x1(t)有界。由文献[12]知,稳定系统在有界输入作用下仍然稳定,故系统稳定需且只需x˙2(t)=-0.9x2(t)-x2(t-τ)稳定。
由定理2知


表1 例1稳定条件比较
2 小结
运用复变函数理论及几何方法得到了一维时滞线性系统稳定的充分必要条件,本文结论的证明过程和表达形式均较以往文献简洁,所以更适合工程应用。最后给出的实例表明了本文方法是有效的。
[1]RICHARD J.Time-delay systems:An overview of some recent advances and open problems [J].Automatica,2003(39):1667-1694.
[2]张冬梅,俞立.线性时滞系统稳定性分析综述[J].控制与决策,2008,23(8):841-848.
[3]CORLESSRM,GONNETGH,HAREDEG,et al.On the Lambert Wfunction[J].Advances in Computational Mathematics,1996(5):329-359.
[4]HALEJK.Theory of function differential equations[M].New York:Spinger 2 Verlag,1977.
[5]俞元洪.超越函数det(aii-biie-λτ-δiiλ)零点全分布在复平面左半部的代数判据[J].科学通报,1984,29(23):1413-1415.
[6]LI X,SOUZA CE.Criteria for robust stability and stabilization of uncertain linear systems with state-delay[J].Automatica,1997,33:1657-1662.
[7]NICULESCUSI,NETOA T,DIONJM,et al.Delay-dependent stability of linear systemswith delayed state:An LMIapproach[C].New Orleans:LA,1995:1495-1496.
[8]LEE Y S,MOON Y S,KWON W H,et al.Delay-dependent robust H control for uncertain systems with a state-delay[J].Automatica,2004,40:65-72.
[9]PARK P.Adelay-dependent stability criteria for systems with uncertain time-invariant delays[J].IEEE Trans on Automatic Control,1999,44(4):876-877.
[10]FRIDMAN E,SHAKED U.An improved stabilization method for linear time-delay systems[J].IEEE Trans on Automatic Control,2002,47(11):931-1937.
[11]XUShengyuan,LAM J.Improved Delay-Dependent Stability Criteria for Time-Delay Systems[J].IEEETrans on Automatic Control,2005,50(3):384-387.
[12]黄琳.控制系统中的线性代数[M].北京:科学出版社,1981:351.

