考虑剪切效应时双模量梁弯曲变形的计算
吴 晓,赵均海,黄志刚,杨立军
(1.湖南文理学院土木建筑工程学院,中国常德,415000;2 长安大学建筑工程学院,中国西安 710061)
在实际工程中,许多工程结构由双模量材料制成,即由拉压弹性模量不同的材料制成.铸铁、金属合金和混凝土等材料都具有拉压弹性模量不同的双模量特性,已有文献对双模量结构在外载荷作用下的变形进行了计算分析.文献[1~2]采用有限元法分析了双模量材料板的变形,文献[3]采用细观力学研究了双模量泡沫材料等效弹性模量,文献[4]研究了双模量材料的本构关系,文献[5~8]对双模量材料结构弯曲及扭转变形进行了计算分析,文献[9]研究了双模量梁的弯曲变形,但是没有研究剪切效应对双模量梁的弯曲变形影响;文献[10]证明了轴向载荷对双模量梁中性轴位置有较大影响.基于上述因素,本文给出了双模量梁剪切弹性模量的表达式,证明了横向外载荷对双模量梁的中性轴位置无影响,并采用Timoshenko 梁理论研究了双模量梁的弯曲变形,分析讨论了剪切变形效应对双模量梁弯曲变形的影响.
1 剪切弹性模量表达式
对于图1所示纯剪切应力状态,可知双模量结构受力单元体的应力与应变关系为

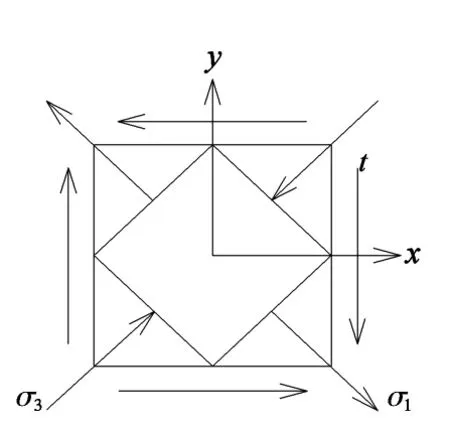
图1 应力状态Fig.1 Sutress state
由于σ1=τ,σ3=-τ,所以
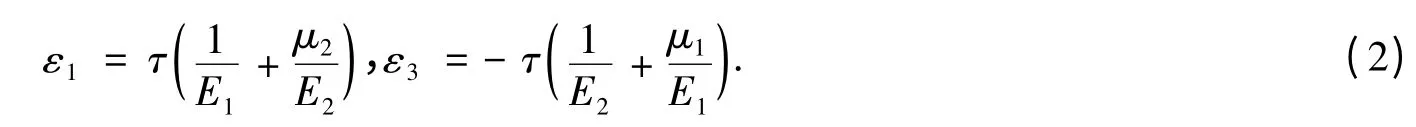
由材料力学可知应变公式为


由式(2)、式(3)和式(4)可以求得
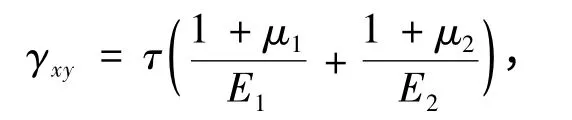

式中,E1和μ1分别为拉伸弹性模量和泊松比,E2和μ2分别为压缩弹性模量和泊松比.
2 确定中性轴位置
由于双模量梁在外载荷作用下弯曲时,会形成弹性模量不同的拉伸区和压缩区,由弹性理论可知双模量梁弯曲时的应力和应变关系为

假设图2所示双模量简支梁在任意载荷作用下发生弯曲变形,以A 点为力矩支点可知


图2 任意载荷作用下简支梁Fig.2 Simply supported beam under loads
由式(7)可知

简支梁的支座约束反力确定后,即可方便写出简支梁任意截面的弯矩表达式M(x).
由弹性理论可知双模量梁弯曲时横截面内力应满足以下关系式

虽然双模量梁在任意载荷作用下其截面弯矩在不同梁段是不相同的,但其曲率是轴向坐标的函数与梁高无关,将式(6)代入式(8)中可求得

式中,h1为拉伸区高度,h2为压缩区高度,
由以上推导可知双模量梁中性轴的位置与作用在梁上的横向载荷无关.
3 双模量梁挠曲线方程
对于图3所示任意载荷作用下的双模量梁,可把分布载荷及集中载荷用奇异函数表示为


图3 任意作用下双模量梁Fig.3 Bimodulous beam under loads
奇异函数的规则为
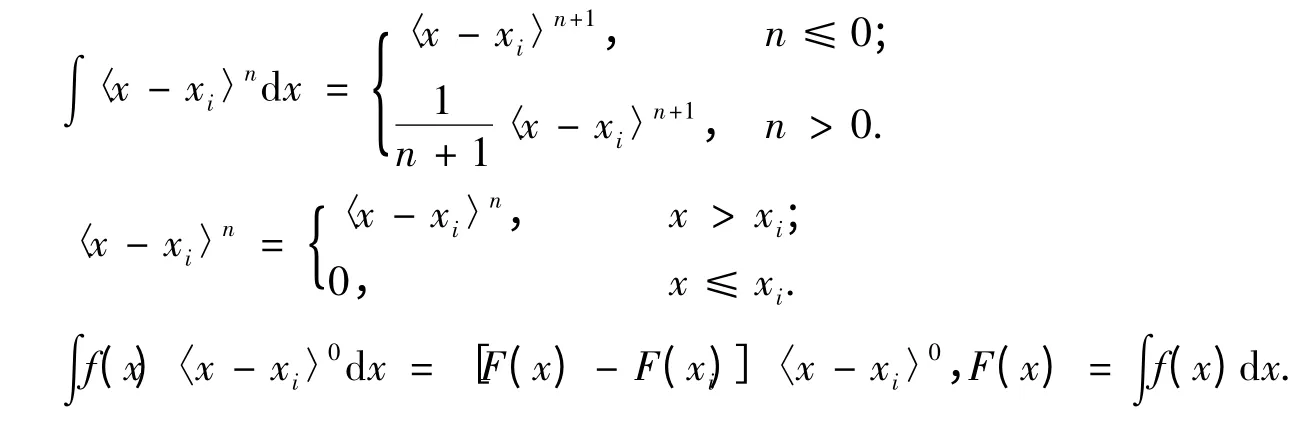
根据Timoshenko 梁理论可知双模量梁弯矩和剪力为

梁横截面平衡方程为

将式(10)代入式(11)可得到下式

对式(12)进行积分可得
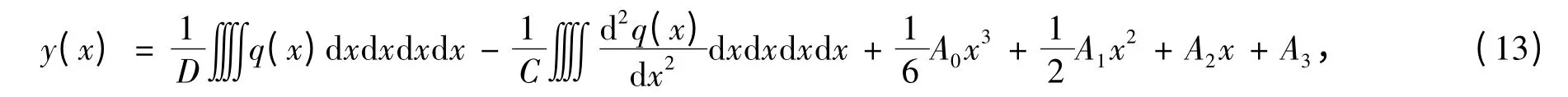
把式(9)代入式(13)中可得双模量梁挠曲线表达式为

以简支双模量梁为例,可知其边界条件为
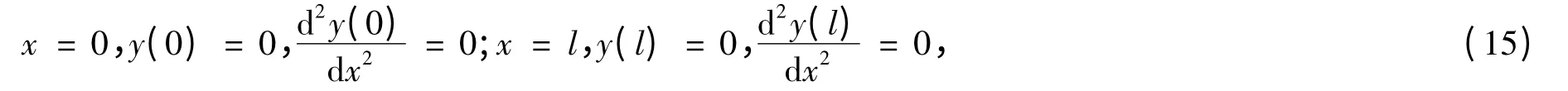
利用式(15)可求得简支双模量梁挠曲线函数中的常数为
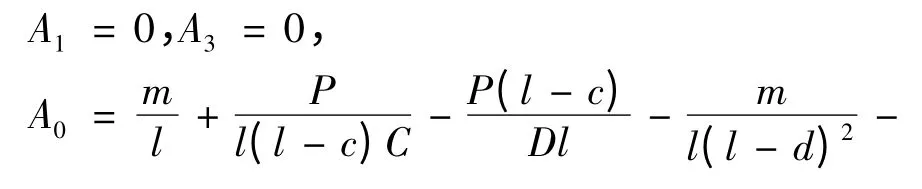

对于其他边界条件支承的双模量梁的挠曲线表达式,利用其边界条件及式(14)即可方便求得.
4 算例分析
下面以实例研究剪切效应对双模量梁弯曲变形的影响.
算例1对于图4所示均布载荷作用下双模量简支梁,由式(16)可求得


图4 双模量简支梁Fig.4 Simply supported bimodulous beam
把A0和A2表达式代入式(14)中可得到均布载荷作用下双模量简支梁挠度为

所以,双模量简支梁中点挠度为

由于工程上要求误差应控制在5% 以内,所以应有下式成立

由式(18)可得到

算例2对于图5所示集中载荷作用下双模量简支梁,由式(16)可求得
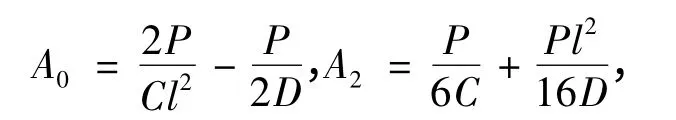

图5 双模量简支梁Fig.5 Simply supported bimodulous beam
把A0和A2表达式代入式(14)中可得到集中载荷作用下双模量简支梁挠度为

所以,双模量简支梁中点挠度为

对于集中载荷作用下双模量简支梁,同理可得

由式(21)可得到

式(19)和式(22)即为考虑剪切效应对双模量简支梁弯曲变形影响时的判别式.
下面以有机玻璃双模量材料为例,讨论分析剪切效应对双模量简支梁弯曲变形的影响.双模量材料参数为:E1=172 GPa,μ1=0.34,E2=295 GPa,μ2=0.395.其中,由式(5)可求得G=80 GPa.具体计算结果见表1 和表2.表中误差为忽略剪切效应与考虑剪切效应时双模量简支梁中点挠度的差值绝对值与考虑剪切效应简支梁中点挠度的比值.

表1 均布载荷作用下双模量简支梁中点挠度Tab.1 The midpoint deflection of simply supported bimodulous beam under uniform load

表2 集中载荷作用下双模量简支梁中点挠度Tab.2 The midpoint deflection of simply supported bimodulous beam under concentrated load
由式(17)和式(20)可知当c →∞时,即为忽略剪切效应时双模量简支梁在均布载荷或集中载荷作用下中点的挠度,这说明本文推导双模量梁的挠曲线通式是正确的.从以上算例可知,本文在考虑剪切变形的基础上,采用Timoshenko 梁理论研究了双模量梁的弯曲变形问题,通过奇异函数得到了双模量梁在横向外载荷作用下的挠曲线通式,利用双模量梁在横向外载荷作用下的挠曲线通式可以方便计算出双模量梁的弯曲挠度.对表1 进行分析可知有机玻璃双模量材料简支梁在均布载荷作用下当时,可以忽略剪切变形的影响;对表2 进行分析可知有机玻璃双模量材料简支梁在集中载荷作用下时,可以忽略剪切变形的影响.
5 结论
通过上述推导证明与实例分析可知:
(1)得出了双模量梁剪切弹性模量的表达式.
(2)采用材料力学原理证明了双模量梁中性轴位置与作用在梁上的横向外载荷无关.
(3)在考虑剪切变形的基础上,采用Timoshenko 梁理论研究了双模量梁的弯曲变形问题,利用奇异函数可以方便得到双模量梁在横向外载荷作用下的挠曲线通式.
(4)对表1 进行分析可知有机玻璃双模量材料简支梁在均布载荷作用下当时,可以忽略剪切变形的影响;对表2 进行分析可知有机玻璃双模量材料简支梁在集中载荷作用下当接近时,可以忽略剪切变形的影响.
[1]MEDRI G.A nonlinear elastic model for isotropic materials with different behavior in tension and compression[J].Trans ASME,1982,26(104):26-28.
[2]SRINIVASAN R S,RAMACHANDRA L S.Axisymmetric nonlinear dynamic response of bimodulous annular plates[J].J Vib Acous,1990,112(2):202-205.
[3]李战莉,黄再兴.双模量泡沫材料等效弹性模量的细观力学估算方法[J].南京航空航天大学学报,2006,38(4):464-468.
[4]蔡来生,俞焕然.拉压模量不同弹性物质的本构[J].西安科技大学学报,2009,29(1):17-21.
[5]吴 晓,杨立军,孙 晋.双模量圆板弯曲变形的计算分析[J].西安建筑科技大学学报:自然科学版,2009,41(1):88-92.
[6]吴 晓,黄 翀,孙 晋.双模量悬臂梁在分布载荷作用下的Kantorovich 解[J].湖南科技大学学报:自然科学版,2012,27(2):55-59.
[7]吴 晓,杨立军,孙 晋.用双模量理论分析灰铸铁拉伸与扭转的破坏试验[J].湖南科技大学学报:自然科学版,2011,26(3):51-54.
[8]吴 晓.用Kantorovich 及Galerkin 联合法研究双模量板的弯曲[J].西安建筑科技大学学报:自然科学版,2012,44(4):457-461.
[9]周小平,卢 萍,张永兴,等.不同拉压模量弹性地基梁的解析解[J].重庆大学学报:自然科学版,2007,30(7):78-82.
[10]姚文娟,叶志明.不同模量弯压柱的解析解[J].应用数学和力学,2004,25(9):901-909.

