一种基于因果网络的支持向量回归特征选择算法

陈一明

(广东石油化工学院实验教学部，中国茂名 525000)

对候选特征进行维数约简在支持向量回归(SVR)预测中占有重要地位，其学习能力很大程度上依赖特征集的选择.尽管实验表明［1］，支持向量机在先进行特征选择后往往比不进行特征选择的预测效果好，而且能很大程度上提高训练速度，但是要严格地确定特征集大小很困难.近十年来，虽然很多特征选择算法被提出［2-4］，但目前还没有一种能完全确定特征集的方法.

目前适用于SVR 的特征选择算法大都基于最大依赖性准则(Max-Dependence)［5］.在特征选择中，最大依赖性准则目的是寻找一个包含m 个特征的集合S，使得该集合与待预测变量y 之间存在最大的依赖关系(依赖关系一般使用互信息来评估)，如式(1)所示.

实际操作中，由于候选特征往往是高维的，很难在高维上对公式(1)进行估算.鉴于此，一些学者提出了解决方法.例如MRMR 算法［2］，利用最大相关性准则(Max-Relevance)和最小冗余性准则(Min-Redundance)来逼近公式(1);MRMS 算法［3］则利用最小冗余性准则(Min-Redundance)和最大显著性准则(Max-significant)对公式(1)进行概率性估算;MIGS 算法［4］同样利用(条件)互信息对公式(1)的值进行估算.尽管使用这些特征选择方法后，SVR 能够一定程度地提升学习精度和速度，但仍然无法完全确定真实的特征集.这些方法有一个共同的缺点，如图1所示.

图1 因果网络模型Fig.1 Causal network model

其中，y 为需要预测的目标变量，X={x1，x2，x3，x4，x5}为y 的候选特征集，且满足图1所示因果网络模型［6］.显然，{x2，x3，x4}为y 的直接因果特征，即满足y=f(x2，x3，x4)，所以y 可以完全由{x2，x3，x4}确定.实际上，由于在这样的结构里，{x1，x5}对于y 的依赖性往往要比{x2，x3，x4}大，现存的特征选择算法一般都会将{x1，x5}首先加入特征集队列里，在其后的交叉验证等方法里也很难将{x1，x5}移除.一方面，这样直接造成了特征集冗余;另一方面，根据每个特征选择算法的各自的机制，有可能会将{x2，x3，x4}其中的点移除.显然，这样都会影响SVR 的预测准确率.

与现存的特征选择算法不同，因果网络是一种对可观测数据进行强有力推理的工具，可以方便地表示和分析确定性和概率性的事物.在因果推断的问题中，利用其可以有效地识别与待预测变量有着因果关系的特征.基于此，提出了一种基于因果网络且适用SVR 的特征选择算法.该算法将传统的基于逼近最大依赖性准则的特征选择算法转移到因果网络的识别上来，直接对要进行预测的目标变量进行因果推断，找出其因果特征集，找到了一种可以确定特征集的方法.仿真数值实验和在应用真实数据集的实验结果表明，该算法应用在SVR 模型上，预测的精确度要高于其他特征选择算法.

1 预备知识

1.1 因果网络

因果网络是表示变量间概率依赖关系的一个有向无环图(DAG)，其可表示为一个三元组G=(X，E，P).其中，X={x1，x2，…，xn}表示该DAG 中所有节点的集合.E={e(xi，xj)|xi，xj∈X}表示DAG 中每两个节点间单向边的集合，其中e(xi，xj)表示xi，xj间存在依赖关系xi→xj.P={P(xi|paxi)|xi，paxi∈X}是条件概率的集合，其中P(xi|paxi)表示xi的父节点集paxi对xi的概率性影响.因果网络本质上就是联合概率分布P(x1，x2，…，xn)的一种图形化表示.

1.2 d-分离准则

d-分离是描述因果网络节点间关系的一个重要图准则.设X，Y，Z 是DAG 中任意3 个互不相交的节点的集合，称Z 在图G 中d-分离节点集X 和Y，如果对任意的从X 的节点到Y 的一个节点的路P 均被Z 阻断，也就是路径P 上存在一个节点xi满足下列其中一个条件:

(1)xi在P 上存在碰撞箭头，即→xi←，且xi及其后代节点都不属于Z;

(2)xi在P 上不存在碰撞箭头，即→xi→或←xi→，且xi∈Z.

根据d-分离准则的概率密度含义［6］，如果集合X 和Y 被集合Z d-分离，那么在给定Z 情况下X 和Y 独立.相反地，如果集合X 和Y 没有被集合Z d-分离，那么给定Z 后X，Y 是相互依赖的.

2 因果推断与最大依赖性准则

信息理论［7］提供了一个直观的途径去估算变量间的依赖关系，其中互信息是一个关键的概念.假设待预测变量y 有着n 个候选特征X={x1，x2，…，xn}，若其中唯一的m 个特征组成的集合Sm满足最大依赖性准则，则选用Sm做特征向量进行SVR 预测往往能达到最好的效果［3］.而现时大部分的特征选择方法仅仅对最大依赖性进行逼近.由于采用的大都是启发式的搜索方法，如果非因果特征对于y 的依赖性较大，很容易在算法的开始阶段就加入了特征集序列.与传统特征选择算法不同，基于因果网络的因果推断方法可以直接找到满足最大依赖性的特征集.

定理1如果待预测变量y 唯一的m 个特征组成的集合Sm满足最大依赖性准则Sm)，则Sm不包含y 任何的非因果特征.

证根据d-分离准则的联合概率密度含义［6］，y 与任何非因果特征集X 都可以被Sm(或Sm的一个子集)D 分离，因而有I(y;X|Sm)=0.由于I(y;X|Sm)=I(y;X，Sm)－I(y;Sm)，故I(y;X，Sm)=I(y;Sm)，即能从X 身上获得的关于y 的信息，已全部被包含在Z 内.另一方面，由于y 与其因果特征集Sm不被任何其他的特征d-分离，有I(y;Sm|X)≥0.事实上，只有当Sm，X 之间满足信息无噪声传输且可逆映射关系时，等号才成立.因此，在实际应用上总有I(y;X)≤I(y;Sm).即若要保持最大依赖性准则，Sm不能包含y 的任何非因果特征，否则必存在冗余.

定理2如果待预测变量y 唯一的m 个特征组成的集合Sm满足最大依赖性准则Sm)，则Sm包含y 所有的因果特征.

证假设x 是不包含在Sm内的y 的一个因果特征，根据d-分离准则的联合概率含义，y 与其因果特征x不被任何其他的特征Smd-分离，有I(y;x|Sm)＞0.由于I(y;x|Sm)=I(y;x，Sm)－I(y;Sm)，故I(y;x，Sm)＞I(y;Sm)，即能从x 身上可以获取得到Sm中没有的关于y 的信息.显然这与最大依赖性准则的定义矛盾.所以Sm包含y 了所有的因果特征.

注定理1 和定理2 说明了寻找待预测变量的因果特征和寻找满足最大相关性准则的特征集是等价的，因果特征集唯一地满足最大相关性准则，这也是因果推断算法能解决特征选择问题的一个重要理论依据.

3 算法的基本流程

如图2所示，因果推断算法的目的是找出预测变量y 的直接因果特征.对于任意一个变量集X={x1，x2，…，xn}，y 为待预测变量，用S(y)表示y 的特征节点集.这里主要利用基于约束的方法［8-9］对带预测变量y的直接因果特征进行识别.相对于目前的特征选择算法，对因果特征直接进行识别，一定程度可以排除虽然满足最大依赖性准则却非直接关联的特征，同时也从理论上找到了一种可以确定特征个数的方法.原则上，任何因果推断算法均可使用，但不同算法往往有着不同的机制，从而可能会产生不同的结果，在一些情况某些算法可能反而不及基于互信息的特征选择方法下SVR 的预测准确率高.如IGCI［10］，ANM［11-12］等算法无法应用于较高维数据.在这里，基于一种具有很好伸缩性、鲁棒性的BUSSM 算法［13］的思想，并对其进行改良，使之适合应用于发现因果特征，具体如下.

算法开始时，先令y 的特征节点集S(y)={}.

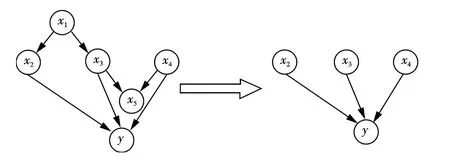
图2 算法的基本框架Fig.2 Algorithm framework

步骤1应用独立性测试:测试X 中y 的每一个候选特征{x1，x2，…，xn}和y 之间的独立性，若独立性Ind(y;xi)成立，表明xi没有携带任何关于y 的信息，即xi不可能y 的因果特征，将xi从X 中移除.当候选特征较多，非因果基因的移除大大降低了算法的时间耗费，而且有助于提高算法的准确率.

步骤2将任意的xi∈X 加入到S(y)，应用条件独立性测试:Ind(y;xi|U)，U 为S(y)xi的任意一个子集合，若条件独立Ind(y;xi|U)成立，表明xi携带的关于y 的信息都被包含在U 中了，即xi不可能为y 的因果特征，则从S(y)中移除特征xi.

步骤3重复步骤2，直到X 中所有特征迭代完，最后得到特征集S(y).

步骤4由于特征集里元素按随机顺序加入，因而可能存在非因果特征保留在S(y)中，这时进行进一步的条件独立性测试:对于任意的xi∈S(y)，U 为S(y)xi的任意一个子集合，测试Ind(y;xi|U).若y，xi被U d-分离，同样表明xi携带的关于y 的信息都被包含在U 中了，即xi不是y 的因果特征，将xi从S(y)中移除.

步骤5经过以上步骤，得到待预测变量y 的特征集S(y)，然后结合SVR 中惩罚参数C，核宽度g 进行参数寻优，得到最优参数利用SVR 模型对目标变量进行预测.

为了方便表述，记上述提出的算法为Causal Feature Selection(CFS)，其具体实现方式如下:

CFS 算法的时间复杂度分析:该算法的时间复杂度与所含因果特征的个数有关，与加入顺序也有关，下面进行具体分析.

1)假设y 有n 个特征，其中仅有一个为因果特征，且为该因果特征被测试的第一个，则在步骤1 中，变量数n*T 独立性测试的时间复杂度，步骤2 和3 的时间复杂度因为都是条件集为单哥变量的独立性测试，时间复杂度都略大于O(T)，所以最好的情况下，该算法的时间复杂度近似O(n*T).

2)假设y 有n 个特征，都为因果特征，此时节点测试顺序和算法时间复杂度无关，在步骤1 中，容易得时间复杂度为O(T).在步骤2 中，S(y)变量数n 与变量可能存在的子集个数形成的关系为:n 个点的集合的子集个数是2n－1，故其算法复杂度为:O(2n*T)，其中T 为每次条件独立性测试的时间复杂度，不是恒值，仅为容易表示.步骤3 中，由于每次条件集规模一样，同理得算法复杂度为:O(2n*n*T)，故该算法的整体时间复杂度为:O(2n*n*T).

实际上，这两种极端条件都很难出现，在一般情况下，不同对特征变量测试顺序导致的算法运行时间差距不大;另一方面，在正常情况下，算法复杂度也远远没达到O(2n*n*T).

4 数值实验

数值实验在Matlab 2010b 中完成，分别用虚拟网络数据和真实数据集对CFS进行评价.在虚拟网络的数据生成阶段，每个节点的数据由图3 中节点的拓扑序列依照函数:y=w1*f1(x1)+w2*f2(x2)+ε 生成.其中w1，w2为每个函数的权值，随机取值于0.3 与0.7 之间;f1(*)，f2(*)是随机函数，等概率取于常见的几种初等函数{sin x，cos x，ex，x2，x3};x1，x2为y 的父节点，ε 为高斯分布的添加噪声.而在真实数据集方面，采用广州某蓄冰供冷站对集运系统的供冷数据对提出的算法进行评估.在算法实现过程中，条件独立性测试使用基于核函数且适用于连续型数据的测试算法KCI-test［14］，阈值δ=0.05.

图3 虚拟网络数据Fig.3 Virtual network dataset

4.1 虚拟网络实验

首先，利用CFS 算法对目标变量y 进行特征选择，得到特征集F1={x2，x3，x4}.显然，从图3 可以看出，F1满足y 因果特征的条件:y=f(x2，x3，x4).考虑到在这种因果网络结构下，现存的特征选择算法挑选出来的特征集几乎都会包含{x1，x5}.所以，在这部分实验中分别选取4 种特征集F1={x2，x3，x4}，F2={x1，x5}，F3={x1，x2，x5}，F4={x1，x2，x3，x4，x5}对目标变量y 进行预测.另一方面，考虑到实际上噪声对SVR 预测的影响，实验分别以ε={0，0.01，0.02，0.05，0.1，0.2}6 种不同程度的噪声进行实验，所有实验均进行1000次，取实验结果的平均值.

如图4所示，以特征集F1和F4进行预测的结果曲线几乎是重合的，但明显要比在F2和F3的情况下要好，其原因是F1和F4都包含了目标变量y 的所有直接因果特征.但由于F4的维度明显比其余特征集高，其训练速度比其余久.在候选特征集规模很大的情况下，覆盖所有候选特征基因进行SVR 预测往往很难操作.而F1仅仅覆盖了目标变量y 的直接因果特征，由于y 由其因果特征确定，所以在选用F1的情况下，其准确率不低于其他任何特征集.同时，也可以看出不同特征对SVR 的抗噪声能力不同，F1和F4对应的曲线相对于F2和F4在噪声增加时，预测的准确率下降速度慢.下面将利用真实数据对CFS 算法进行进一步的验证.

图4 在4 种特征集下SVR 算法的预测结果Fig.4 The results of SVR with 4 different feature sets

4.2 真实数据实验

表1 真实数据集下的实验结果Tab.1 The results of real world dataset

在本节实验中，采用广州某供冷站对集运系统从2011年4月14 号到2013年11月11 号的943 天的供冷数据，针对提出的算法进行评估.其中前800 天数据用作训练，后143 天数据用作模型检验.在用SVR 模型进行预测前，采用CFS 算法对候选的16 个特征集:{明天最高温度、明天最低温度、明天最高湿度、明天最低湿度、明天平均湿度、昨天最高温度、昨天最低温度、昨天最高湿度、昨天最低湿度、昨天平均湿度、昨天用冷量、两天最高温度差、两天最低温度差、两天最高湿度差、两天最低湿度差、两天平均湿度差}进行特征选择，最终得到特征集为第{1，2，5，7，11，14}6 个特征.为了进行算法对比，利用常用的特征选择方法MIGS同样挑选前6 个特征，按顺序为{11，2，7，1，6，5}.可以看到CFS 和MIGS 挑选的结果仅有1 个不同，这也一定程度显示了CFS 的适用性，另外由于全部候选特征仅有16 个，这里也全选特征进行对比实验.

由表1 可以看出，在准确率上CFS 仅微优于全选的结果，由偏差程度对比中也可以看到两者极为接近.而MIGS 所选的6 个特征中，由于遗漏了对制冷量有着直接因果关系的特征，因而效果不如前两者的结果.真实实验的结果再一次表明，CFS 算法适用于SVR 特征选择，能准确地识别带预测变量的直接因果因素.而其他的特征选择算法都仅基于对最大依赖性准则逼近，这些算法在得到的特征序列中，非因果特一般排在了因果特征前面，导致了特征集过大或遗漏因果特征，从而影响了SVR 的学习能力.

上述实验表明，CFS 算法应用在SVR 上有着优良的效果.事实上，虽然因果特征对待预测变量起着决定性作用，但这并等同于一定要包含因果特征的特征集适用于SVR 时才能达到最高的准确率.在某些情况下，特征集不包含因果特征，也可能达到不逊于因果特征集的准确率.

CFS 算法旨在从理论上将因果网络与特征选择结合起来，并为SVR 提供一种可以完全确定特征集的途径.虽然CFS 算法从理论上解决了一直无法找到准确特征集的问题，但由于现存的条件独立性测试算法相对于互信息计算对变量的样本量需求更高，在样本量不充分的情况下，应用在SVR 上CFS 也有可能不及传统的基于互信息的方法，这有待于条件独立性研究的发展.

5 结语

与传统的基于互信息的支持向量回归特征选择不同，本文采取了基于因果网络的特征选择方法，一方面利用条件独立性测试寻找带预测变量的直接关联特征，排除了虽然满足最大依赖性却非直接关联的特征;另一方面也从理论上找到了一种能确定特征个数的方法.文中采用虚拟网络数据和真实数据集进行实验，结果表明该算法应用在支持向量回归预测上优于其他特征选择算法.

［1］CAO L J，CHUA K S，CHONG W K，et al.A comparison of SA，KSA and ICA for dimensionality reduction in support vector machine［J］.Neurocomputing，2003，55(1):321-336.

［2］PENG H，LONG F，DING C.Feature selection based on mutual information criteria of max-dependency，max-relevance，and min-redundancy［J］.Patt Anal Machine Intel，IEEE Trans，2005，27(8):1226-1238.

［3］MAJI P，GARAI P.On fuzzy-rough attribute selection:criteria of max-dependency，max-relevance，min-redundancy，and maxsignificance［J］.Appl Soft Comput，2013，13(9):3968-3980.

［4］CAI R，HAO Z，YANG X，et al.An efficient gene selection algorithm based on mutual information［J］.Neurocomputing，2009，72(4):991-999.

［5］MAJI P，PAUL S.Rough set based maximum relevance-maximum significance criterion and gene selection from microarray data［J］.Int J Approx Reason，2011，52(3):408-426.

［6］PEARL J.Causality:models，reasoning and inference［M］.Cambridge:The MIT press，2000.

［7］COVER T M，THOMAS J A，Elements of Information Theory［M］.New Jersey:Wiley，2005.

［8］SPIRTES，GLYMOUR C，SCHEINES R.Causation，prediction，and search［M］.Cambridge:The MIT Press，2000.

［9］TSAMARDINOS I，BROWN L E，ALIFERIS C F.The max-min hill-climbing Bayesian network structure learning algorithm［J］.Machine Learning，2006，65(1):31-78.

［10］JANZING D，MOOIJ J，ZHANG K，et al.Information-geometric approach to inferring causal directions［J］.Artif Intell，2012，56(10):5168-5194.

［11］HOYER P O，JANZING D，MOOIJ J，et al.Nonlinear causal discovery with additive noise models［C］//Advances in Neural Information Processing Systems.Vancouver，Canada:MIT Press，2009:689-696.

［12］PETERS J，JANZING D，SCHOLKOPF B.Causal inference on discrete data using additive noise models［J］.IEEE Trans Patt Anal Machine Intell，2011，33(12):2436-2450.

［13］CAI R，ZHANG Z，HAO Z.BASSUM:A Bayesian semi-supervised method for classification feature selection［J］.Patt Recog，2011，44(4):811-820.

［14］ZHANG K，PETERS J，JANZING D，et al.Kernel-based conditional independence test and application in causal discovery［EB/OL］.(2012-02-14)［2013-10-24］.http://arxiv.org/ftp/arxiv/papers/1202/1202.3775.pdf.