基于交互式粒子群算法的部队卫生装备巡修行程规划设计

庞剑飞，蒋俊成，马 翠

基于交互式粒子群算法的部队卫生装备巡修行程规划设计

庞剑飞，蒋俊成，马 翠

目的：建立基于交互式粒子群算法的部队卫生装备巡修行程规划模型，提高行程制订的科学性、经济性。方法：首先将行程规划问题转换为一类特殊的旅行商问题，之后采用交互式粒子群算法进行求解，并利用相对距离给定法与可量化属性有效地缓解用户在评价过程中的疲劳，最后通过对实际巡修任务进行求解，验证模型的可行性、有效性。结果：该模型能够根据实际巡修任务制订出满足任务需求与行车要求的行程，并在时间、费用等方面尽可能令用户满意。结论：该模型可行性高、有效性强，其推广应用能够有效提高部队卫生装备巡修的效率与效益。

部队卫生装备；巡修行程规划；交互式粒子群算法

0 引言

卫生装备是部队卫生机构遂行卫勤保障任务的物质基础，加强卫生装备的维修保障，保持装备完好率，对于维护官兵健康，提升部队战斗力具有重要意义[1]。在全军联勤保障体系下，部队卫生装备的维修主要依靠总部所—军区所—区域性检修站三级检修机构完成，各级卫生机构定期将需要维修的装备上报，总部所将维修需求汇总，并按照保障范围进行任务分配，各检修机构根据分配的维修任务制订巡修计划，在规定的时间内完成维修并上报维修情况[2-3]。维修机构在巡修时，由于保障范围广，维修地点多，常常需要跨省市进行，如何根据维修任务制订最经济合理的巡修行程计划是巡修人员面临的难题[4]。鉴于此，本文首先将巡修行程规划转换为一类拓展的旅行商问题（travelling salesman problem，TSP）问题并利用交互式粒子群算法进行求解，以期为巡修人员制订一条在花费、舒适度等方面均尽可能满意的巡修计划，并在提高卫生装备巡修效率的同时降低巡修成本。

1 行程规划分析

巡修行程规划与旅游行程规划问题类似，均属于旅行商问题的一个拓展[5]，巡修人员要在规定时间内完成对多个维修需求点的维修保障，制订一条最合理的巡修行程，从巡修机构所在地出发，每个维修需求点访问一次，最后返回出发地点。行程的制订不仅要求交通费用、时间等可量化的指标最优，还要考虑舒适度、个人偏好、情感等主观因素，属于隐性目标决策问题，也是非决定性多项式完成（non-deterministic polynomial complete，NPC）问题[6]。

1.1 基本概念定义

对某一检修机构，其保障范围内假设有n个维修需求点，需求点集合表示为DP={vi｜i=1，2，…，n}。

（1）行程段。维修需求点vi与vj组成的序偶，可表示为（vi，vj），其中i≠j，表示vi到vj的行程，包括时间、路程等。

（2）行程T。维修需求点的排列，表示对维修需求点的巡修顺序。T=（0，vi1，vi2，…，vin，0），其中，0表示出发点，是集合的一个排列。

（3）单元属性。维修需求点的信息，如维修点的维修任务耗时、到达时间、离开时间等。

（4）双元属性。行程段上的信息，如两维修需求点之间的时间花费、距离等。

（5）行程属性。巡修行程的具体路线所展示的信息，如总的费用、时间花费等。

1.2 行程规划模型建立

在某一检修机构的保障范围内，巡修人员需要制订一条经济合理的行程来完成对维修需求点的装备维修任务，即制订一条在费用、时间、舒适度等方面使巡修人员最满意的行程。

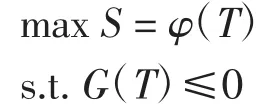
式中：T∈NM，NM为所有可能的行程集合；S为行程的满意度；G为行程需满足的限制条件。

满意度不仅包括可量化的指标，如行程的距离、时间花费、费用花费等，还包括不能或难以量化的值，如巡修人员对到达需求点时间偏好等，因此满意度函数φ不能完全表示，无法通过解析方法得到最优行程。对于此类问题，常采用交互式智能算法（IEC）求解，即借助人的智能信息处理能力给出解方案的适应度，使算法进一步搜索更好的解。采用交互式智能算法，让巡修人员人工地对行程进行评价，促使问题向巡修人员满意的方向收敛，通过智能体的进化，实现主观情感空间向客观特征空间的映射，最终得到满意的行程。其中，巡修人员的评价值即为问题的适应度F（fitness），可表示为

式中：A（attribute）为行程T的属性集；λ为巡修人员的心理偏好评价函数，是根据个人的知识、经验和偏好等对行程的主观评价。

2 算法设计与实现

2.1 标准粒子群算法

粒子群算法（particle swarm optimization，PSO）是一种智能进化算法，从随机解出发，采用“群体”与“进化”的概念，通过迭代寻找最优解并使用个体的适应值评价解的优劣[7]。该算法将每个鸟儿看作是D维搜索空间中一个没有质量和体积的粒子，在空间中只有一块食物，每只鸟儿（粒子）按一定速度在空间中移动，寻找这块食物，这块食物的位置即为最优解，每个粒子飞行时根据周围粒子和自身的位置调整速度的方向和大小直至寻找到最优解。设粒子的种群规模为m；粒子i的位置为zi=（zi1，zi2，…，ziD），根据要解决的问题设定适应度函数并计算zi当前的适应值；vi=（vi1，vi2，…，viD）为粒子的飞行速度；pi=（pi1，pi2，…，piD）为粒子i目前搜索到的最优位置；pg=（pg1，pg2，…，pgD）为整个粒子群目前搜索到的最优位置，粒子的位置和速度更新公式为

式中：i=1，2，…，m；d=1，2，…，D；k为迭代次数；r1和r2为[0，1]之间的随机数；c1为粒子跟踪自己历史最优值的权重系数，表示粒子自身的认识，称为“认知”，通常设置为2；c2为粒子跟踪群体最优值的权重系数，表示粒子对整个群体知识的认识，称为“社会知识”，一般设置为2；ω为惯性权重，衡量粒子的全局搜索能力与局部搜索能力。

2.2 改进的粒子群算法

行程规划问题的解空间为离散空间，用PSO求解需对标准粒子群算法中粒子的位置、速度以及操作进行重新定义[8]。

2.2.1 粒子的位置

行程规划问题的结果是得到具有最优大用户满意度的哈密尔顿圈，其状态空间即为所有行程的集合。粒子的位置可定义为一个包括所有维修需求点与出发点的哈密尔顿圈，即序列x=（n0，n1，…，nN，n0），其中ni∈E，E为状态空间，设所有ni与ni+1之间的路径存在。

2.2.2 粒子的速度

速度定义为粒子位置的置换序列集，表示一组置换序列的有序列表，可表示为v={（ik，jk）｜（ik，jk）∈{1，2，…，N}，k∈{1，2，…，}}，即先交换粒子中ik、jk的位置，然后交换ik+1、jk+1的位置，依此类推；表示该速度所含交换的数目。

2.2.3 粒子位置、速度、实数间的操作

粒子位置与速度的加法操作表示将一组置换序列依次作用于某个粒子位置，从而得到一个新位置，即新的行程排列。例如：位置为{l，5，2，4，3，l}+ {（2，4）}={1，5，4，2，3，1}。

粒子位置与位置相减后结果为一组置换序列，即速度。粒子速度与速度的加法操作为2个置换序列的合并，结果为一个新的置换序列，即一个新的速度。

实数c为[0，1]的任意实数，设速度v为k个置换序列，则乘法操作为对速度的置换序列进行截取，使得新的速度的置换序列长度为｜c×k｜（c×k取整）。

2.2.4 公式更新

粒子的速度、位置及其各种操作重新定义后，离散粒子群算法的速度更新公式表示如下：

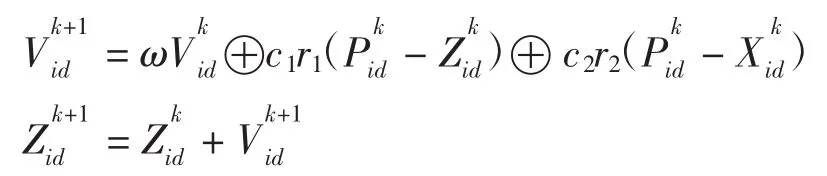
式中，c1、c2、r1、r2与标准PSO算法中定义相同；⊕为两交换序列的合并算子，表示速度与速度的加法操作；“－”表示粒子位置与位置的减法操作；“＋”表示粒子位置与速度的加法操作。

2.3 算法描述及策略

2.3.1 算法流程

图1给出了交互式粒子群算法的流程，其计算过程如下：

（1）设定算法有关参数，包括种群数量、最大迭代次数、惯性权重等；

（2）随机生成指定数量的粒子作为初始种群；

（3）巡修人员标记当代最优粒子，并据此产生适应度；

（4）满意度判断，若巡修人员对当代最优行程满意，则结束，否则，进行下一步；

（5）终止条件判断，若已到达最大迭代次数，则结束，否则，转（6）；

（6）粒子群更新，根据速度与位置更新公式产生种群新的位置，转（3）。

图1 交互式粒子群算法流程

2.3.2 适应度策略

将行程T的属性A分为可量化与不可量化2个部分，其中可量化部分包括总距离、总花费（油耗、住宿等）、总时间；不可量化评价部分包括到达时间、离开时间等。虽然算法中粒子种群规模较小，但对每代个体进行评价易导致用户疲劳，若进一步减少种群规模的话，则会影响算法的收敛速度，为此，采用相对距离给定法[9]与可量化行程属性来计算适应度。首先用户在每代种群中选出一个最满意的行程个体作为最优个体，并给予固定的适应度值F，则其他粒子的适应度FE按下式计算：

式中：RD为粒子与最优粒子之间路径的相对距离；AT为粒子的可量化属性。

对于行程T1与T2，其路径相对距离计算如下：

式中：L为个体的程度即维修需求点的数量；Ls为T1、T2最长相同子路径的程度；S为最长相同子路径的位移；C为归一化后行程的总花费；WT为总时间；α、β∈R，表示权重。

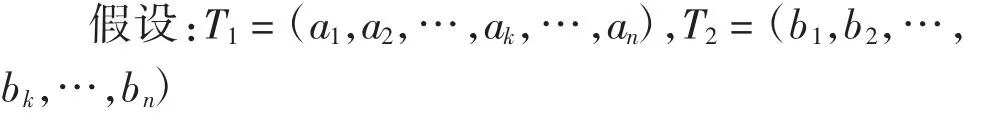
式中：（ai，ai+1，…，ai+m）和（ai+k，ai+k+1，…，ai+k+m）是T1、T2最长相同子路径，其相对位移为

2.4 仿真实验及分析

以某三级维修站某年度维修任务为研究实例，在保障区域内有A1～A15共计15个维修需求点，具体位置见表1。在巡修之前需对各点维修时间进行预判（见表2）。假设汽车行驶的平均速度为70 km/h，人员住宿标准为100元/（人·d），燃油消耗为15 L/100 km，汽油价格为7.6元/L，巡修人员每天的工作时间为10 h，巡修行程是从维修站所在地出发，依次完成全部维修需求点的维修任务之后返回驻地，两地间的距离采用公路距离。

表1 维修需求点位置分布

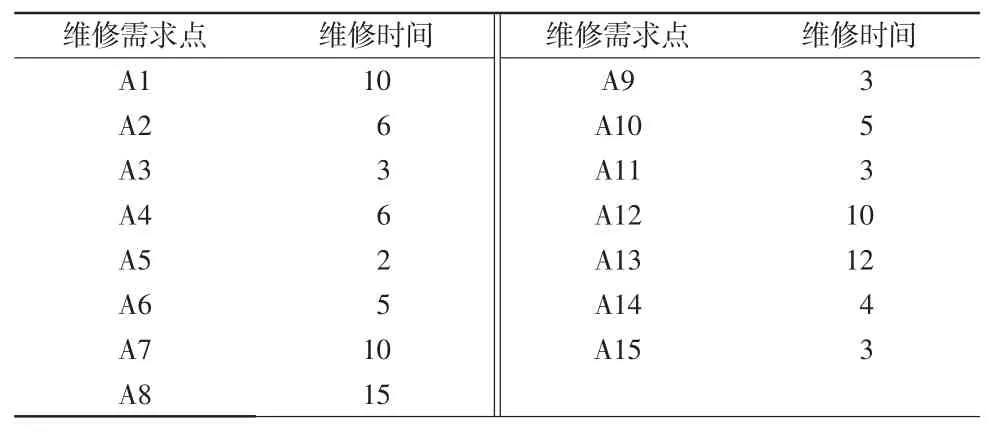
表2 各维修需求点维修时间估计 h

具体行程安排时需满足以下原则：（1）人员的工作时间为8：00—18：00，可适当加班，但不超过1 h；（2）行车时间为8：00—22：00。

将粒子群算法中种群规模设置为20，初始惯性权重为0.96并随迭代次数增加而递减，最大迭代次数设为200，则权重分别为0.5、0.6；个体行程显示总路程、总花费、总时间及各点到达、离开时间等项目;算法结束方式为达到最大迭代次数或用户手动结束2种。利用Matlab对算法进行实现，邀请巡修人员进行评价，最终计算得到最满意巡修行程如图2所示，具体安排见表3。

图2 巡修行程示意图

表3 巡修行程具体安排 h

最满意行程总路程为2 099 km，总的巡修时间为12 d，总的花费（油耗、住宿、过路费）为4 852元。通过修改指标权重及行程要求还可制订不同偏好、不同要求的行程方案，如时间较短、花费较少、加班较少等。

3 讨论

本文利用交互式粒子群算法对部队卫生装备巡修行程规划问题进行了建模与求解，帮助巡修人员制订花费少、效率高同时兼顾舒适度的巡修路线与安排。模型采用交互式粒子群算法对行程进行寻优，引入用户评价机制，在迭代过程中，让用户对个体的适应度（满意度）进行评价，标记出用户对行程个体满意度，从而引导粒子群向用户最满意的位置移动。采用相对距离给定法使用户仅需在对少量行程个体进行评价的情况下完成适应度计算，减轻用户疲劳。与人工制订行程相比，本文提出的方法工作量小、操作简单，能够对总行程时间、费用花费进行有效控制。本文讨论的卫生装备巡修行程规划是在巡修前通过对行程时间、维修时间等因素的预测进行的，实际巡修时可能会出现突发状况，如维修时间增加或提前、扰乱既定的行程、对后续的行程不能按计划进行等情况，可通过对剩余巡修任务的分析重新制订用户满意的行程。算法可进一步推广至其他行程规划问题，如旅行规划、部队巡诊等。

[1]罗自力，何湘，荀鲁川.部队卫生装备维修保障工作形势与对策[J].西南国防医药，2012，22（2）：209-211.

[2]方铁，胡红波.卫生装备管理服务网的设计与实现[J].医疗卫生装备，2013，34（8）：37-39.

[3]蒋忠伟，方梅华.医院医疗设备维修管理方案的设计[J].医疗卫生装备，2013，34（8）：40-42.

[4]汤献国，胡莹.卫生装备巡检巡修工作实践与探索[J].医疗卫生装备，2014，35（8）：134-136.

[5]陆青，粱昌勇，黄永青，等.面向旅游行程规划的交互式多智能体遗传算法木[J].计算机应用研究，2008，25（11）：3 311-3 313.

[6]陆青.基于IEC的隐性目标智能决策方法研究[D].合肥：合肥工业大学，2009：20-24.

[7]曾建潮，介婧，崔志华.微粒群算法[M].北京：科学出版社，2004：12-18.

[8]Onwubolu，Godfrey C，Babu B V.New Optimization Techniques in Engineering[M].Berlin：SpringerBerlinHeidelberg，2004：219-239.

[9]许芳诚．智能型多准则决策支持研究：以交谈式遗传算法为基础的模型[D].台湾：国立中央大学，2000．

（收稿：2014-08-12 修回：2014-12-20）

Military medical equipment maintenance itinerary planning based on interactive particle swarm algorithm

PANG Jian-fei1,2,JIANG Jun-cheng1,MA Cui3
（1.Department of Medical Engineering,the 117th Hospital of the PLA,Hangzhou 310013,China;2.No.73232 Unit of the PLA,Zhoushan 316217,Zhejiang Province,China;3.Teaching and Research Section of Mathematics and Biomathematics, School of Biomedical Engineering of the Third Military Medical University,Chongqing 400038,China）

ObjectiveTo realize military medical equipment repair itinerary planning based on interactive particle swarm algorithm.MethodsItinerary planning was transformed into some traveling salesman problem,and then interactive particle swarm algorithm was utilized to solve the problem.The users′fatigue was alleviated efficiently during the evaluation process by methods of relative distance and quantifiable attributes.A solution was made based on practical maintenance to prove the feasibility and availability of the model.ResultsThe route planning model could make work schedule and traffic plan based on practical maintenance tasks and requests,which could also satisfy users with time cost,expenses, etc.ConclusionIt proves that the route planning model is of feasibility and availability by solution towards practical issues,thus can greatly improve efficiency and benefit of military medical equipment maintenance.[Chinese Medical E-quipment Journal，2015，36（3）：17-20]

military medical equipment;maintenance itinerary planning;interactive particle swarm algorithm

R318；TP18

A

1003-8868（2015）03-0017-04

10.7687/J.ISSN1003-8868.2015.03.017

重庆市自然科学基金项目（CSTC2013jcyjA10041）

庞剑飞（1989—），男，助理工程师，主要从事医学图像处理、医疗仪器维修与管理方面的研究工作，E-mail：jian11fei.happy@163.com。

310013杭州，解放军117医院医学工程科（庞剑飞，蒋俊成）；316217浙江舟山，解放军73232部队（庞剑飞）；400038重庆，第三军医大学生物医学工程学院数学与生物数学教研室（马 翠）

马 翠，E-mail：macui4956@163.com