基于马氏距离的雷达网有源假目标干扰鉴别技术

杨 忠，王国宏，孙殿星，贺达超，刘 源

（海军航空工程学院a.研究生管理大队；b.信息融合研究所，山东烟台264001）

基于马氏距离的雷达网有源假目标干扰鉴别技术

杨 忠a，王国宏b，孙殿星a，贺达超a，刘 源a

（海军航空工程学院a.研究生管理大队；b.信息融合研究所，山东烟台264001）

针对雷达网有源假目标干扰问题，为了消除长基线雷达组网时地球曲率对数据处理的影响，通过坐标转换，将各雷达站的目标的量测数据转化到了地心直角（ECEF）坐标系内，得到统一坐标系下的目标量测信息，完成空间上的对准；在此基础上，基于虚假目标的量测与雷达站位置有关，真实目标量测与雷达站无关，因而依据卡方分布的性质，在ECEF坐标系内对各个量测进行卡方检验，鉴别出虚假目标；最后，通过仿真验证了分析的正确性，该算法与工程实际接轨，实用性较强。

长基线；雷达网；距离多假目标欺骗干扰；ECEF坐标系；坐标变换

现代战争中电子战快速发展，相比于压制干扰，欺骗干扰可利用雷达的匹配滤波增益，以较小功率达到更好的干扰效果，更适合干扰跟踪雷达[1-3]。欺骗式干扰机采用数字射频存储器（DRFM）等先进的转发式干扰装置，截获雷达发射信号并快速精确复制、调制和转发，产生多个距离假目标，具有较强的迷惑性，严重消耗了宝贵的雷达资源，对其研究有重要意义[4-7]。

针对距离多假目标干扰，已经有大量的研究成果，文献[8]利用真目标的位置信息识别真假目标，文献[9]联合利用真目标的位置信息及速度信息剔除虚假目标，进一步降低了组网雷达被欺骗概率，文献[10]提出了一种基于神经网络和模式识别技术的目标与干扰的识别方法，在检测概率和稳定性上都优于传统方法。对雷达来说，目标的测量通常都是在以雷达站为中心的极坐标系中完成的，后续的目标量测数据处理则是在以雷达站为中心的直角坐标系中完成的。现有的研究把组网雷达所在地表看成一个平面，直接通过平移和旋转变换把雷达站的数据统一到公共笛卡尔坐标系上[11]。但地球是一个近似椭圆的旋转体。当雷达网中2节点距离很远时，由于地球曲率的影响，直接进行平移和旋转变换，目标信息将会产生很大的误差，并且2站距离越远误差越大。同时，在实际工程应用中，雷达站和目标的的位置信息都是在地理坐标系下标注的，因而必须将地理坐标系下的坐标转化到以雷达站为中心的直角坐标系内。为消除地球曲率的影响，可以采用一个中间坐标系作为过渡。WGS84坐标模型的坐标系（ECEF）是一个地心固定的绝对坐标系，可以用它来作为过渡坐标系[12]。

本文的背景设为距离多假目标干扰下的长基线雷达组网，先将真实目标和虚假目标的量测数据统一到地心直角坐标系（ECEF）内，得到统一坐标系下的目标量测信息；然后，通过卡方检验鉴别虚假目标[13]；最后进行了仿真验证，仿真结果表明本文方法可将真实目标量测成功关联，而虚假目标量测则会被剔除。

1 问题描述

如图1所示，假设位于地理坐标系的2部雷达组网对目标进行定位跟踪，其中雷达1的经、纬、高为(L1,B1,H1)，雷达2的经、纬、高为(L2,B2,H2)。

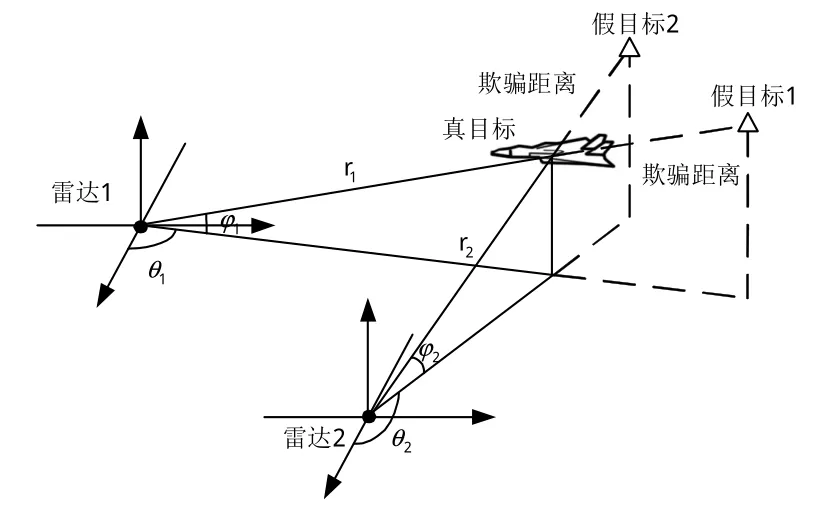
图1 雷达网目标鉴别模型Fig.1 Distinguish model of radar Network target

雷达在ECEF坐标系内的坐标(xR,i,yR,i,zR,i)为[14]：

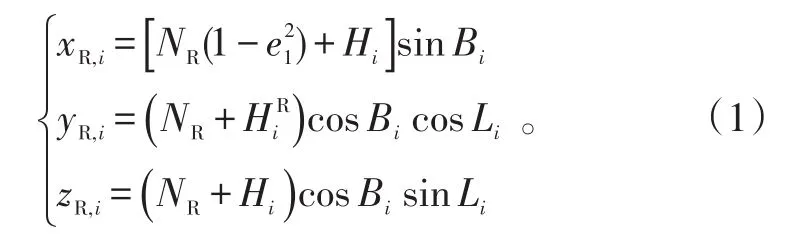
设k时刻目标在雷达i局部坐标系中的极坐标为(ρi(k),θi(k),φi(k))，直角坐标为(xi(k),yi(k),zi(k))，易得[14]：

在ECEF坐标系中，目标的坐标(xECEF(k),yECEF(k),zECEF(k))为[14]：

式（2）、（3）的转换方程中包含了非线性转换，所以直角坐标系下的估计结果为有偏估计。通过对其补偿可得到更准确的结果，补偿后的目标坐标为[14]：

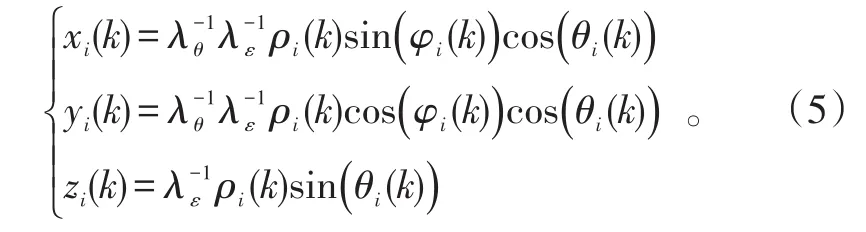
式（2）～（5）中：k=1,2,…,N；i=1,2。

补偿后的量测噪声协方差的各元素分别为：

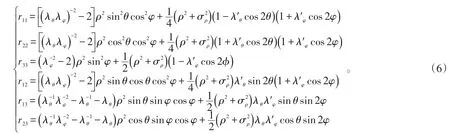
2 模型分析

分析图1可知，距离多假目标干扰与雷达和干扰机在同一条直线上，所以虚假目标的空间位置与雷达站的地理坐标有关，雷达站不同时，虚假目标的位置也不同；而真实目标与雷达站是相互独立的，真实目标的位置与雷达站地理位置无关。因此，在雷达网信息处理中心进行数据处理时，可以根据不同雷达站位置的不同鉴别出虚假目标。

在本文的背景下，设在雷达i局部极坐标系下，真实目标的极坐标为(ρT,i(k),θT,i(k),φT,i(k))(i=1,2)，距离多假目标干扰在雷达上形成多个虚假点。此处，选择最具代表性的2个虚假点进行分析。设虚假目标的极坐标(ρJ,i(k),θJ,i(k),φJ,i(k))(i=1,2)为[14]：

式中，i表示雷达1或雷达2。在得到极坐标系下的量测之后，根据雷达站的位置信息，可以将目标量测统一到ECEF坐标系。在ECEF坐标系中，采用最近邻法关联来自不同雷达的量测数据。

令：

为研究雷达量测的差异程度，最简单的就是构造2个量测间的距离。而欧氏距离虽然很有用，但其明显的缺点是没有考虑到量测坐标的协方差。为此，本文选用量测点的马氏距离为统计量，克服了量测误差协方差对统计量的不良影响。设统计量：

因此，根据基于统计判决的雷达网数据关联准则，来自不同雷达的数据关联问题可以用下面的假设检验做出分析判决：

H0：若η(k)≤λ，则判雷达1和2的量测来自同一真实目标；

H1：若η(k)＞λ，则判雷达1和2的量测来虚假目标。

3 仿真验证

本文假设雷达1的纬度、经度和高度为(26.5,29.5,300)，雷达2的纬度、经度和高度为(27.5,30,300)。2部雷达的距离量测误差标准差为米，角度量测误差标准差为σθ1=σθ2=0.3°。在欺骗距离500 m处产生一个虚假目标，为简单起见，仿真中不妨假设欺骗干扰信号强度大致与真目标回波信号强度一致。Monte Carlo试验次数为100次。干扰机初始纬度、经度和高度为(26.5,30,8 000)，干扰机在纬度、经度和高度方向上的运动速度为(1/360,1/360,0)，设雷达采样周期为1 s，采样时间为500 s。干扰机在欺骗距离为500 m处对2部雷达产生虚假目标。经过时间对准，空间对准，雷达位置和航迹如图2所示。

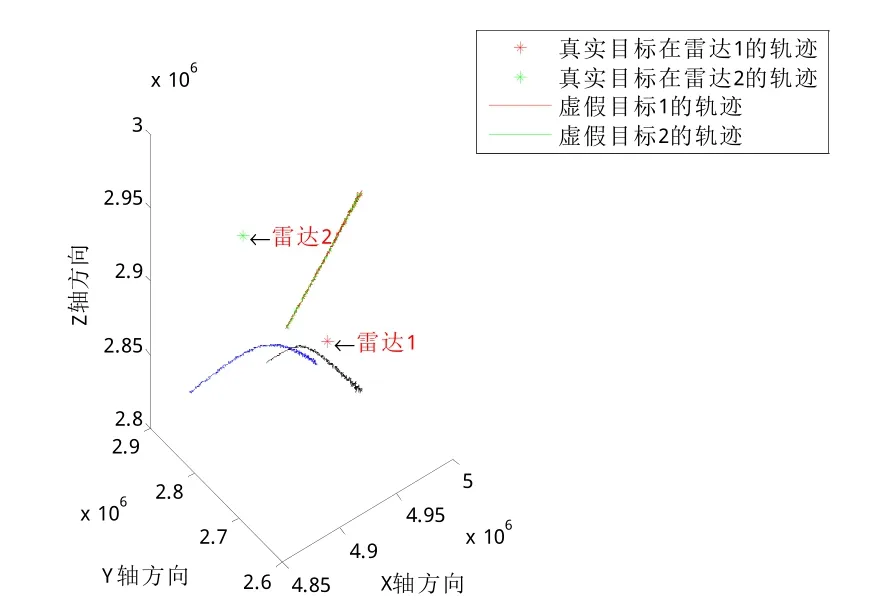
图2 目标航迹图Fig.1 Targets track

从图2可以看出，长基线雷达组网时，由于地球曲率的影响，目标的运动轨迹不再是直线，而是有一定曲率的弧线。此时必须进行无偏转换，才可以得到准确的结果[15]。根据图2的目标运动轨迹，可以得到雷达1和雷达2的真实目标量测之间的马氏距离曲线、雷达1的真实目标量测与雷达2的虚假目标量测的马氏距离曲线、雷达1的虚假目标量测与雷达2的真实目标量测之间的马氏距离曲线以及雷达1和雷达2的虚假目标量测之间的马氏距离曲线，如图3～6所示。

图3 真实目标马氏距离曲线Fig.3 Distance curve of real target mahalanobis

4 虚假目标的马氏距离曲线Fig.4 Distance curve of false-target mahalanobis

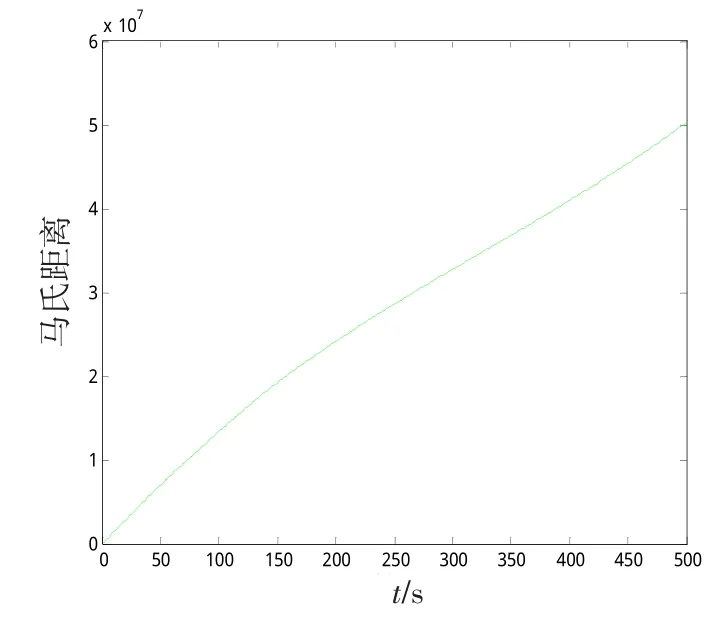
图5 真实目标1与虚假目标2量测的马氏距离曲线Fig.5 Mahalanobis distance between real target 1 and false target 2 measure

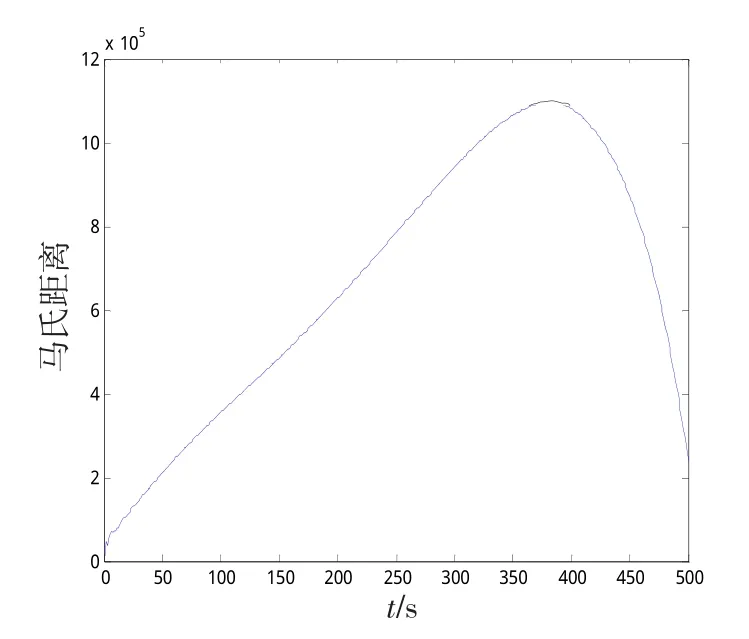
图6 真实目标2与虚假目标1量测的马氏距离曲线Fig.6 Mahalanobis distance between false target 1 and real target 2 measure

比较上图可以看出，真实目标的马氏距离的数量级为104，而虚假目标的马氏距离的数量级为106，远远大于真实目标的马氏距离。因此，在进行点迹关联的时候，选取合适的检验门限，可以将虚假点迹在融合中心滤除。

下面分别对真目标和假目标进行卡方检验，得到目标的关联概率，如图7～10所示。

图7 真实目标量测关联概率Fig.7 Association probability of real target measure

图8 虚假目标量测关联概率Fig.8 Association probability of false target measure

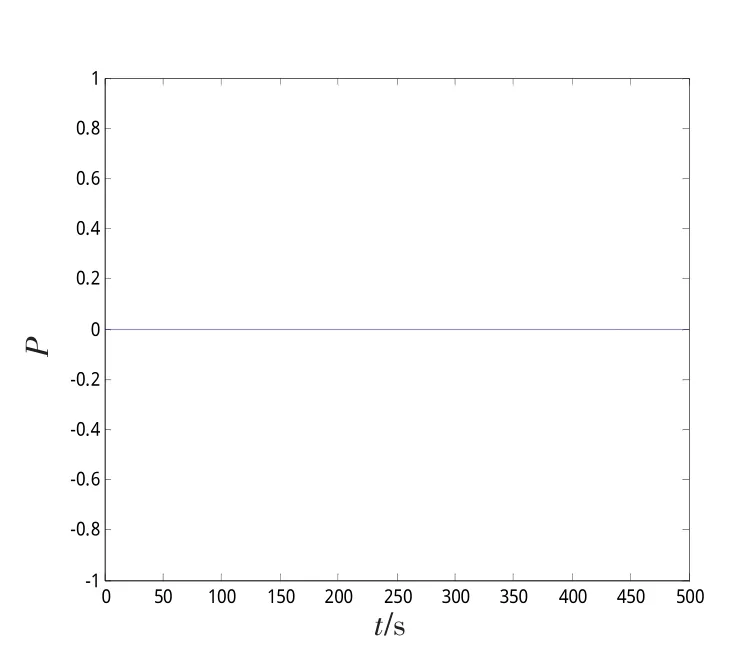
图9 真实目标1的量测与虚假目标2的量测关联概率Fig.9 Association probability between real target 1 and false target 2 measure

图10 虚假目标1的量测与真实目标2的量测关联概率Fig.10 Association probability between false target 1 and real target 2 measure

从图7～10可以看出，真实目标量测由于距离比较近，在ECEF坐标系内进行卡方检验时，很容易关联成同一目标；而虚假目标之间，由于距离相隔较远，无法关联到一起；同理真实目标和虚假目标的量测也由于距离较远而无法关联。

4 结论

本文针对距离多假目标干扰下长基线雷达网抗干扰问题，从原理上分析了长基线雷达组网时，如何消除地球曲率的影响，即将目标量测通过无偏转换转换到地心直角坐标系内；然后，在地心直角坐标系内对来自不同雷达的真实目标量测、虚假目标量测进行卡方检验，得出如下结论。

不同雷达站真实目标量测的马氏距离远小于虚假目标的马氏距离，因而真实目标量测关联到一起的概率也远大于虚假目标量测。这是因为每一个虚假目标由于只是针对单一雷达进行干扰，在空间上不存在相关性。因此，通过融合中心的点迹关联，可以将虚假目标滤除。

[1]SCHLEHER D C.Electronic warfare in the information age[M].Norwood MA：Artech House，2000：155，157.

[2]LI NENGJING，ZHANG YITING.A survey of radar ECM and ECCM[J].IEEE Transactions on Aerospace and Electronic Systems，1995，31（3）：1110-1120.

[3]王超，袁乃昌，闫敦豹.多假目标干扰效果评估准则研究与仿真[J].航天电子对抗，2002（3）：7-11. WANG CHAO，YUAN NAICHANG，YAN DUNBAO. Research and simulation on assessment of Multi-False-Target jamming[J].Aerospace Electronic，2002（3）：7-11.（in Chinese）

[4]杜辉.电子战综述[J].计算机与网络，2005（7）：50-52. DU HUI.Electronic warfare summarization[J].Computer and Network，2005（7）：50-52.（in Chinese）

[5]JING H，LI X R，JILKOV V P，et al.Sequential detection of RGPO in target tracking by decomposition and fusion approach[C]//15thInternational Conference on Information Fusion.Singapore，2012：1800-1807.

[6]OZDIL O，SERIN M，ISPIR M，et al.Channelizer structure in DRFM systems for real signals[C]//IEEE International Conference on Signal Processing and CommunicationsApplication.2013：1-4.

[7]OLIVIER K，CILLIERS J E，DU PLESSIS M.Design and performance of wideband DRFM for radar test and evaluation[J].Electronics Letters，2011，47（14）：824-825.

[8]赵艳丽，王雪松，王国玉，等.多假目标欺骗干扰下的组网雷达跟踪技术[J].电子学报，2007，35（3）：81-85. ZHAO YANLI，WANG XUESONG，WANG GUOYU，et al.Tracking technique for radar network in the presence of multi-range-false-target deception jamming[J].Acta Electronic Sinica，2007，35（3）：81-85.（in Chinese）

[9]赵珊珊，张林让，周宇，等.组网雷达点迹信息融合抗假目标干扰方法[J].电子科技大学学报，2014，43（2）：207-211. ZHAO SHANSHAN，ZHANG LINRANG，ZHOU YU，et al.Measurement fusion method against false-target jamming for radar network[J].Journal of University of Electronic Science and Technology，2014，43（2）：207-211.（in Chinese）

[10]吕强，李建勋，秦江敏，等.基于神经网络的雷达抗转发式距离欺骗干扰方法[J].系统工程与电子技术，2005，27（2）：240-243. LU QIANG，LI JIANXUN，QIN JIANGMIN，et al.Method against radar’s transmitting deceptive jamming in distance based on neural network[J].Systems Engineering and Electronics，2005，27（2）：240-243.（in Chinese）

[11]陈永光，李修和，沈阳.组网雷达作战能力分析与评估[M].北京：国防工业出版社，2006：340-342. CHEN YONGGUANG，LI XIUHE，SHEN YANG.Analysis and evaluation to network radar engagement abilities [M].Beijing：National Defense Industry Press，2006：340-342.（in Chinese）

[12]李杰涛，郭敏.雷达组网中的坐标变换问题[J].火控雷达技术，2007，36（7）：28-42. LI JIETAO，GUO MIN.Coordinate transformation in radar networks[J].Fire Control Radar Technology，2007，36（7）：28-42.（in Chinese）

[13]张尧庭，方开泰.多元统计分析引论[M].武汉：武汉大学出版社，2013：186-190. ZHANG YAOTING，FANG KAITAI.An introduction to multivariate satatistical analysis[M].Wuhan：Wuhan University Press，2013：186-190.（in Chinese）

[14]何友，修建娟，张晶炜，等.雷达数据处理及应用[M].北京：北京电子工业出版社，2006：66-78. HE YOU，XIU JIANJUAN，ZHANG JINGWEI，et al.Radar data processing with applications[M].Beijing：Publishing House of Electronics Industry，2006：66-78.（in Chinese）

[15]LERRO D，BAR SHALOM Y.Tracking with debiased consistent converted measurements versus EFE[J].IEEE Transactions on Aerospace and Electronic Systens，1993，29（3）：1015-1022.

Technic of Discriminating False-Target Deception Jamming for Radar Network Based on Mahalanobis Distance

YANG Zhonga,WANG Guohongb,SUN Dianxinga,HE Dachaoa,LIU Yuana
（Naval Aeronautical and Astronautical University a.Graduate Students’Brigade; b.Institute of Information Fusion,Yantai Shandong 264001,China）

Aiming at multi-range-false-target deception jamming of long baseline radar network,firstly,in order to re⁃move the effect of earth curvature produced by long baseline radar networks,the target position data in geography coordi⁃nate system was transformed to Earth-centred-Earth-fixed(ECEF)coordinate system based on coordinate transformation, simultaneously,target measurements in radar-centred retangular coordinate system were transformed to ECEF too;And in this basis,due to the fact that false target position was relevent to radar position,but real target position information was not,theχ2test to false target measurements was constructed in ECEF based on characteristics ofχ2distribution.Lastly simulation results verified the correctness of the analyses,and this arithmetic is close to engineering realistic,it was practi⁃cable.

long baseline;radar network;multi-range-false-target deception jamming;ECEF;coordinate transformation

TN958.93

A

1673-1522（2015）05-0437-05

10.7682/j.issn.1673-1522.2015.05.008

2015-06-25；

2015-07-31

国家自然科学基金资助项目（61002006，61102165，61102167）；“泰山学者”建设工程专项经费课题资助项目

杨 忠（1989-），男，硕士生；王国宏（1963-），男，教授，博士，博导。