主被动传感器UT-DC目标定位算法
王国宏,盛 丹,于洪波
(海军航空工程学院信息融合研究所,山东烟台264001)
主被动传感器UT-DC目标定位算法
王国宏,盛 丹,于洪波
(海军航空工程学院信息融合研究所,山东烟台264001)
主被动传感器融合定位具有高度非线性,针对采用传统的线性化方法计算变量统计特性,理论定位结果与实际定位结果相差较大的情况,文章提出了基于不敏变换(UT)的数据压缩(DC)融合定位算法。首先,通过不敏变换精确计算了二维变量的统计特性,减小了非线性误差的影响;其次,针对数据压缩过程中量测信息重复利用的问题进行去相关性处理,获得较高的定位精度;最后,通过理论分析和仿真结果验证,相较于传统的线性化处理方式相差较大的情况,基于不敏变换的数据压缩融合定位方法理论结果与实际结果相吻合。
主动传感器;被动传感器;非线性;不敏变换;相关性;数据压缩
压制干扰[1-3]是针对传感器的一种主要干扰手段,严重影响了传感器的检测、识别、跟踪性能[4-6],不仅制约了传感器的作用范围,还会对传感器自身的生存造成威胁。抗压制干扰的一种有效途径是采用多传感器信息融合[7-8],而无源传感器测向交叉定位[9-10]和主被动传感器信息融合定位是常用的2种方式。当传感器都受到严重干扰只能获得目标的方位量测时,可以通过测向交叉定位法进行目标定位和跟踪[11-14],其中,文献[11]考虑了目标到雷达基线的距离为常数的条件下传感器的布局问题,得出了一些有用的结论;文献[12]给出了最小定位模糊区面积准则下多个被动传感器的布站准则;文献[13]将目标到基线的垂直距离与基线长度的比值作为约束条件,通过拉格朗日乘子法求得无源定位系统中的最优交会角;文献[14]给出了两部2D被动传感器在方位和俯仰测角误差不同的情况下,最优交会角与俯仰角的关系曲线。
当部分传感器受到干扰,部分传感器没有受到干扰时,可以采用主被动传感器信息融合法进行目标定位[15-16],其中,文献[15]构建了STMHM算法以解决目标的实时跟踪和识别,但是采用的被动传感器主要是用于目标识别;文献[16]研究了如何实时地切换主被动传感器的问题。在公共的探测区域内,主动传感器能够获得目标的距离和方位信息,被动传感器只能够获得目标位置中的方位信息,从改善定位精度考虑,把被动传感器的量测信息和主动传感器的测量信息进行融合时能否提高定位效果是实际应用中面临的问题,然而,此方面的研究还鲜见相关的报道。
针对上述问题,本文将主被动传感器的量测信息相结合,研究了通过数据压缩(DC)[17]把主动传感器定位结果和主被动传感器交叉定位结果进行融合定位的情况,提出了一种基于不敏变换(UT)[18]和DC的主被动传感器融合定位算法,通过采用不敏变换实现非线性变量统计特性的精确计算,通过最优数据压缩实现主被动传感器信息的充分利用,并在不同的条件下进行了分析和讨论,得出了一些有益的结论。
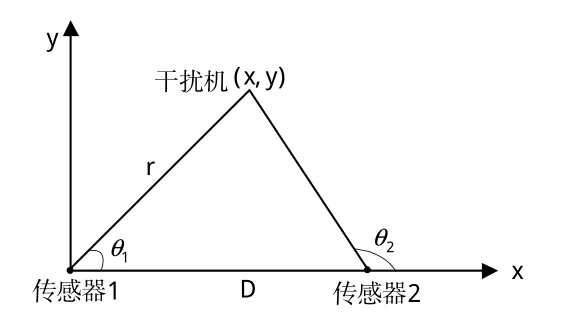
图1 主被动传感器目标定位示意图Fig.1 Target location schematic diagram of active and passive sensors
1 问题描述
假设空中目标为压制干扰机,采用主动传感器1和被动传感器2进行目标定位。为讨论问题方便,假定2部传感器分别位于(0,0)、(0,D),D为传感器1、2的基线长度,传感器1能够获得目标的距离和方位量测r、θ1,传感器2只能获得目标的方位量测为θ2。2部传感器的角度量测误差及主动传感器的距离量测误差相互独立,并且服从均值为0、方差分别为的高斯分布。主被动传感器目标定位关系如图1所示。
主动传感器能够获得目标的距离和方位量测,根据几何关系获得目标位置估计。被动传感器只能获得目标的方位量测,在公共的探测区域内,可利用主被动传感器的方位量测进行交叉定位。主动定位和交叉定位都只采用2个量测信息,为充分利用主被动传感器的量测信息,考虑将主动定位与交叉定位进行数据压缩融合,通过融合定位获得目标位置估计。
2 基于UT-DC最优目标定位算法
根据图1,主动传感器定位结果为:
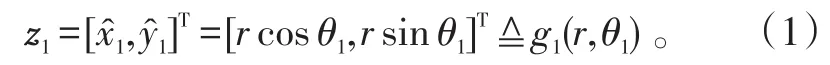
主动传感器和被动传感器利用角度量测进行交叉定位的结果为:
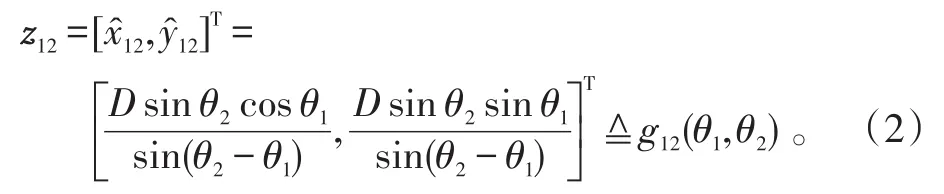
将主动定位和交叉定位结果通过数据压缩加权融合,融合定位结果为:

式中,Q1、Q12分别为主动定位和交叉定位在融合中的权重。
值得注意的是,主动定位和交叉定位都采用了角度量测θ1,因而由式(1)、(2)所得的目标位置估计是相关的,在数据压缩加权融合时要考虑其相关性,此时,加权系数分别为:
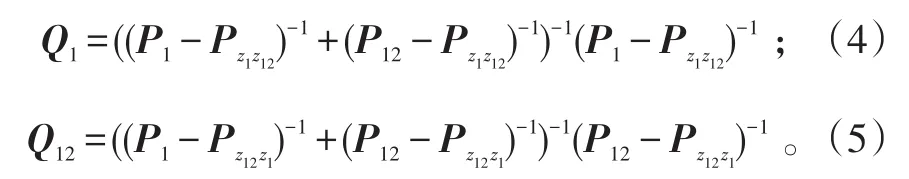
式(4)、(5)中:P1、P12分别为主动传感器定位和主被动传感器交叉定位的误差协方差矩阵;为互协方差矩阵。
忽略相关性,则融合定位时的加权系数可简化为

在本文中,分别将考虑相关性的处理模型(见式(3)~(5))称为模型1,将忽略相关性的处理模型(见式(3)、(6)、(7))称为模型2。
由上可见,主被动传感器进行目标最优定位的关键是位置估计统计特性的计算。由于式(1)、(2)均是传感器测量的非线性方程,目前获得目标位置估计统计特性的方法一般是采用线性化处理的方式,从而有可能在非线性较强的情况下引入较大的误差。而UT是一种针对非线性变换情况下计算随机变量统计特性的有效方法,因而本文考虑采用UT进行位置估计统计特性的计算。
主动传感器定位时,根据不敏变换原理,将传感器1的距离和方位量测构造随机向量x1=[r,θ1]T,随机向量维数为,协方差为

由x1到位置估计z1的非线性映射为

采用不敏变换计算z1的统计特性,对于2维随机向量x1,选取5个sigma采样点vi如下:

其相应的权重wi为

x1的sigma采样点经非线性映射G1后,得到z1的sigma采样点z1i
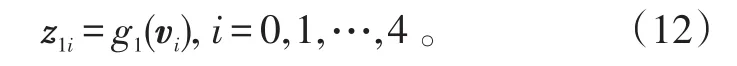
在此变换过程中,相应的权重保持不变。加权得到目标位置估计和相应协方差阵如下:

交叉定位时,根据不敏变换,将传感器1、2方位量测构造随机变量x12=[θ1,θ2]T,,协方差阵为

由量测x12到位置估计z12的非线性映射为:

由于模型1和模型2的差别主要在于是否考虑相关性,因此,分别给出相应的处理方法。

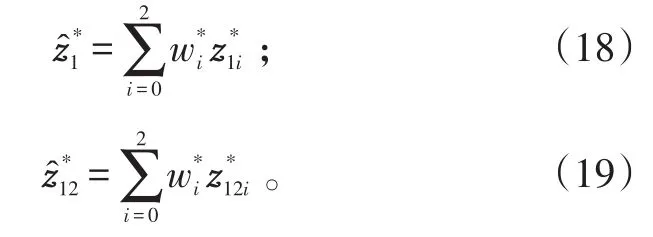
相应的互协方差矩阵分别为:

将式(20)、(21)及P1、P12代入式(4)、(5),得到考虑相关性时融合定位加权系数,结合式(3),考虑相关性时融合后目标位置估计为:
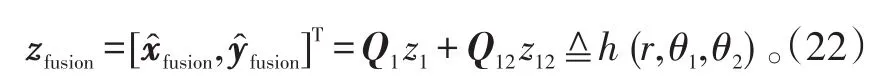
由于融合定位所得的目标位置估计仍然测量向量的非线性函数,因此,仍采用UT来精确计算估计的统计特性。融合后,位置估计是关于距离r、角度θ1和θ2的函数,因此构造随机变量为xfusion=[r,θ1,θ2],维数为nxfusion=3,协方差为

由向量xfusion到位置估计zfusion的非线性映射为
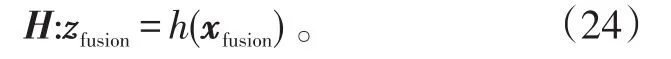
模型2:忽略融合变量间的相关性。将P1、P12代入式(6)、(7),得到忽略相关性时融合定位加权系数。结合式(3),获得目标的位置估计zfusion,其统计特性计算步骤同模型1,最终可得到融合定位的位置估计和误差协方差Pfusion。
3 数值结果与仿真分析
采用目标位置均方根误差来衡量目标的定位效果,根据第2节的结果,得到3种方法的均方根误差。
主动传感器定位的位置均方根误差为

交叉定位的位置均方根误差为

融合定位的位置均方根误差为
通过比较3种定位方法的定位误差,可以获得最优定位算法。
假设传感器1为主动传感器,坐标位置为[0,0],传感器2为被动传感器,坐标位置为[D,0],D=5km,量测误差设定为。2部传感器的交会角θCA在(0°,180°)范围内变化,验证不同的交会角下不同定位方法的定位效果。
1)传统方法目标定位性能。传统定位方法采用线性方式进行统计特性计算,其融合方式采用模型2。
在不同的交会角下,采用传统目标定位方法时,对目标定位的性能分别进行数值计算和仿真验证,结果如图2、3所示。
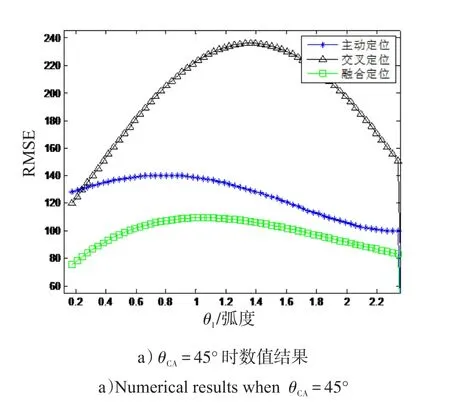

图2 传统方式处理时不同交会角下定位误差数值结果Fig.2 Theoretical results in different cut angle with traditional method
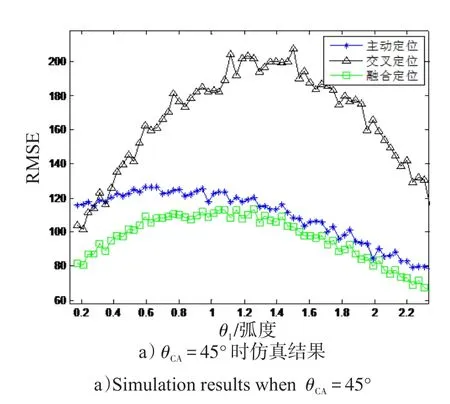
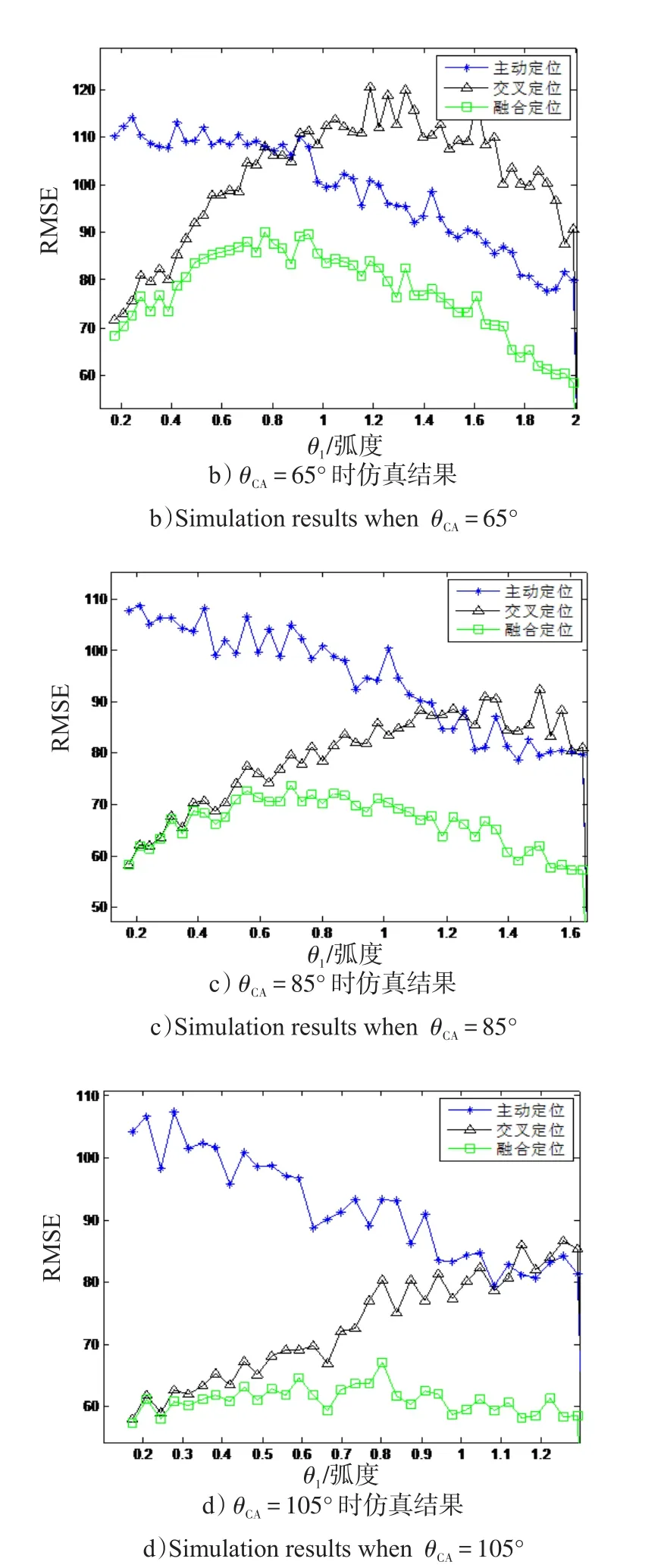
图3 传统方式处理时不同交会角下定位误差仿真结果Fig.3 Simulation results in different cut angle with traditional method
从图2、3看出,不同的交会角下,传统的定位方法与仿真有差异,其中融合定位的差别较为突出。因为主动定位与交叉定位都是非线性的,二者的数据压缩加权融合过程关于量测也是非线性的。因此,目标的融合定位具有高度的非线性,而传统方式采用线性方法进行估计矢量的统计特性计算,从而理论定位结果与仿真结果存在较大的差异。
2)采用UT计算统计特性,模型1进行融合定位时目标定位性能。在不同交会角下,模型1进行融合定位时,对目标定位的性能分别进行数值计算和仿真验证,结果见图4、5。

图4 融合定位模型1误差数值结果Fig.4 Theoretical results in different cut angle with model 1 using UT

图5 融合定位模型1误差仿真结果Fig.5 Simulation results in different cut angle with model 1 using UT
从图4、5可以看出,仿真结果与误差计算结果相吻合,说明了通过UT计算统计特性后,主动定位、交叉定位和模型1融合定位的正确定;从算法的性能比较可以看出,模型1融合定位的结果优于主动传感器定位和交叉定位,这说明引入被动传感器的量测信息可以提高定位精度,进行融合定位能够获得更优的定位效果。
3)采用UT计算统计特性,模型2进行融合定位时目标定位性能。采用UT计算统计特性,在不同交会角下,模型2进行融合定位时,对目标定位的性能分别进行数值计算和仿真验证,结果如图6、7所示。
从图6、7可以看出,仿真结果与误差计算结果相吻合,说明了不敏变换下模型2融合定位的正确性。3种方法中,模型2融合定位的结果最优,这说明融合定位在忽略统计信息的相关性也能够获得更优的定位效果。
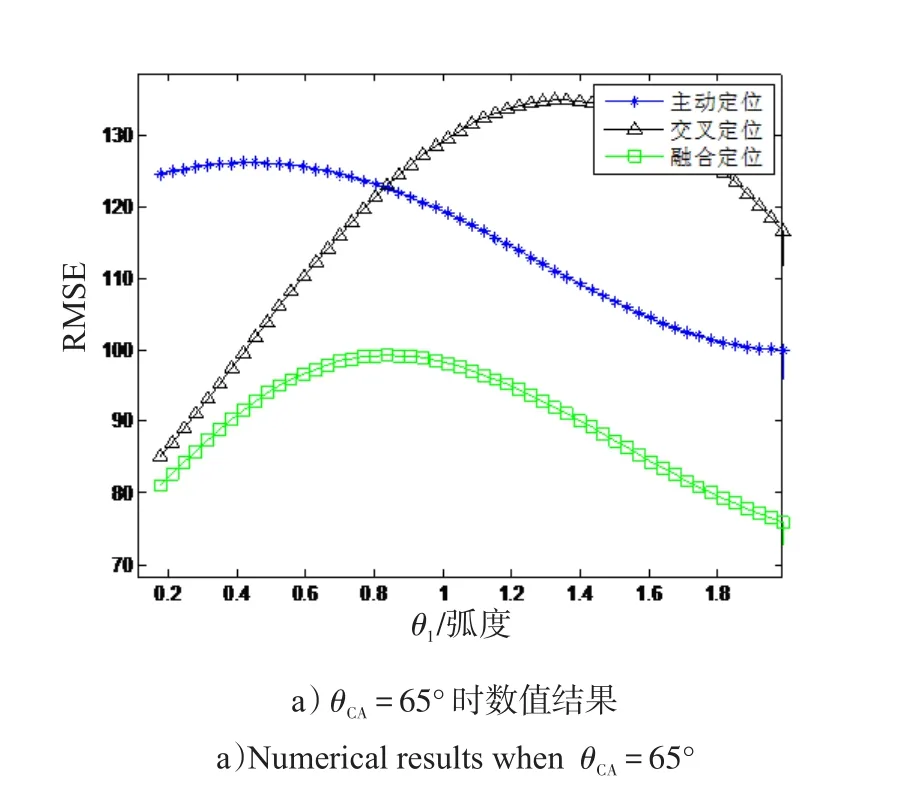

图6 融合定位模型2误差数值结果Fig.6 Theoretical results in different cut angle with model 2 using UT
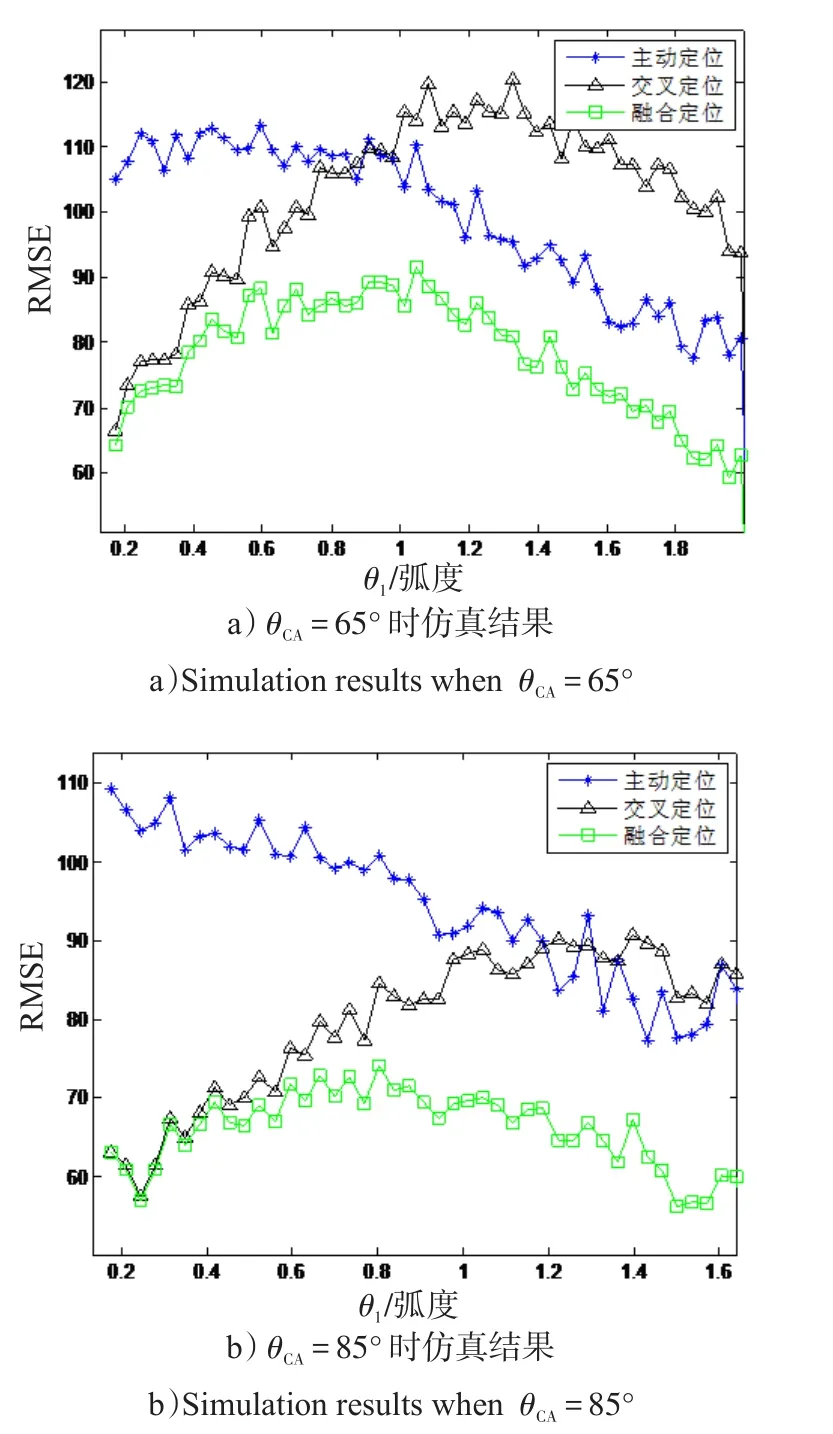
图7 融合定位模型2误差仿真结果Fig.7 Simulation results in different cut angle with model 2 using UT
4)采用UT计算统计特性时,融合定位模型1与模型2定位性能比较。从图4~7可以看出,在采用不敏变换的情况下,融合定位模型1和模型2都能实现对目标的正确估计,并且都要优于主动定位和交叉定位的定位效果。因此,需要对两者的定位效果进行比较来确定最优定位方法的选取。
从图8、9可以看出数值结果和仿真结果是吻合的。从a)、c)可以明显看出,模型1对目标位置估计的精度更高一些,随着交会角的增大,二者的估计误差相差不大,但是模型1仍占有一定的优势。这说明,在融合定位时进行相关性处理可以进一步提高定位精度。
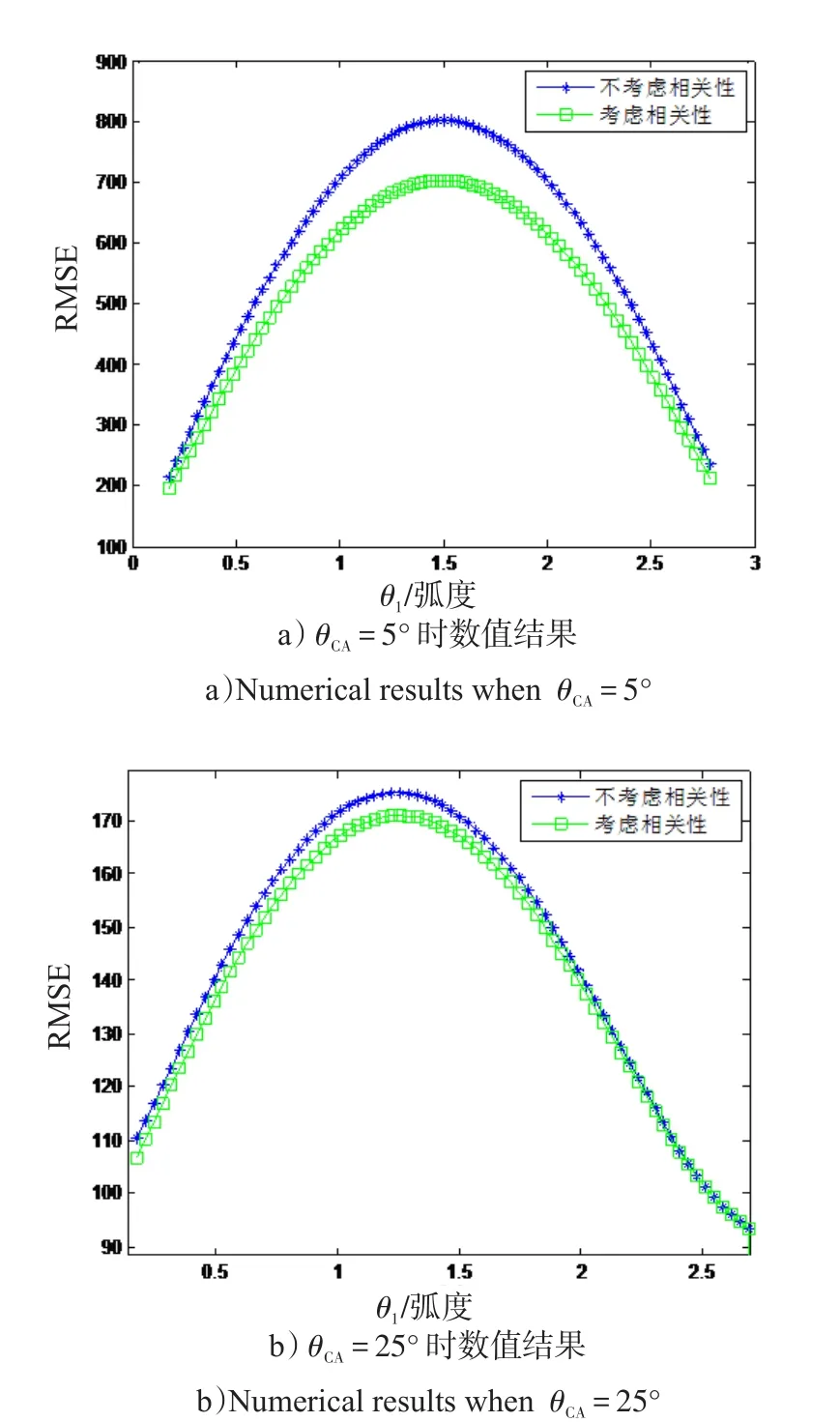
图8 融合定位模型1与模型2定位误差数值结果Fig.8 Theoretical results in different cut angle with model 1 and 2 using UT

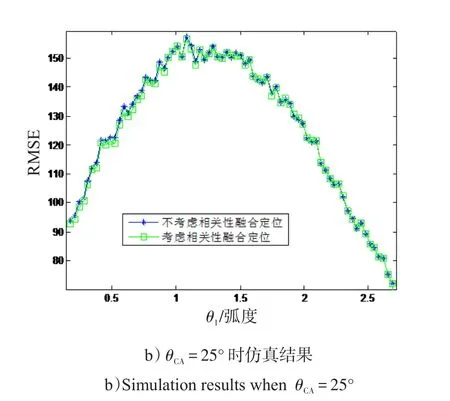
图9 UT变换下模型1与模型2定位误差仿真结果Fig.9 Simulation results in different cut angle with model 1 and 2 using UT
综上,得出结论如下:
1)相较于传统的线性处理方式,采用UT计算统计特性可以减小非线性误差,从而显著提高定位效果;
2)将主动定位与交叉定位结果进行融合,可以更加充分地利用主、被动传感器的信息,因而定位精度更优;
3)在最优数据压缩融合定位时,融合定位模型1的定位精度高于融合定位模型2,说明考虑相关性能够获得更精确的加权系数。
4 结论
本文提出了基于UT-DC的主被动传感器目标定位算法。首先,采用UT进行二维变量的统计特性的计算,相较于传统的线性处理方式,其理论结果与实际结果更加吻合;然后,在融合定位过程中进行了相关性处理,进一步提高了定位的精度;最后,通过数值分析和仿真对本文算法进行了验证,通过比较各定位方法的定位效果,得出采用融合定位能够得到目标最优位置估计的结论。
[1]JING JIA,WEN SHENG.Simulation on detection probability loss of OTHR under oppressive active jamming[J]. Applied Mechanics and Materials,2014,701:544-548.
[2]ZHANG Q Y,CAO B,WANG J,et al.Polarization filtering technique based on oblique projections[J].Science in China:Information Sciences,2010,53(5):1056-1066.
[3]王象,杨建华,闵涛,等.基于雷达对抗试验等效推算的密集压制干扰研究方法[J].宇航学报,2012,33(2):217-221. WANG XIANG,YANG JIANHUA,MIN TAO,et al. Study on densen barrage jamming based on equivalent reckoning of radar ECM test[J].Journal of Astronautics,2012,33(2):217-221.(in Chinese)
[4]LI DAN,LIU J Y,QIAO L,et al.Fault tolerant navigation method for satellite based on information fusion and unscented Kalman filter[J].Journal of Systems Engineering and Electronics,2010,21(4):682-687.
[5]YAN X H,LIU Y G.Global practical tracking nonlinear systems with by output-feedback for unknown growth rate [J].Science in China:Technological Sciences,2011,54(10):2079-2090.
[6]李程,王伟,施龙飞,等.基于多源信息融合的有源雷达组网方式序贯识别方法[J].电子与信息学报,2014,36(10):2456-2463. LI CHENG,WANG WEI,SHI LONGFEI,et al.Sequential method for netting type recognition of active radars based on multi-source information fusion[J].Journal of Electronics&Information Technology,2014,36(10):2456-2463.(in Chinese)
[7]周卫东,刘萌萌,杨永江.基于多传感器信息融合理论的交互式多模型算法[J].华南理工大学学报:自然科学版,2014,42(9):82-89. ZHOU WEIDONG,LIU MENGMENG,YANG YONGJIANG.An improved interacting multiple model algorithm based on multi-sensor information fusion theory[J].Journal of South China University of Technology:Natural Science Edition,2014,42(9):82-89.(in Chinese)
[8]赵珊珊,张林让,周宇,等.组网雷达点迹信息融合抗假目标干扰方法[J].电子科技大学学报,2014,43(2):207-211. ZHAO SHANSHAN,ZHANG LINRANG,ZHOU YU,et al.Measurement fusion method against false-target jamming for radar network[J].Journal of University of Electronic Science and Technology,2014,43(2):207-211.(in Chinese)
[9]HATEM H,KUTLUYIL D.Passive localization of scanning emitters[J].IEEE Transactions on Aerospace and Electronic Systems,2010,40(5):907-910.
[10]YU C,MIKE,CHEN S W.Cross-layer modeling and simulation of circuit reliability[J].IEEE Transaction on Com-puter-Aided Design of Integrated Circuits and Systems,2014,33(1):8-23.
[11]修建娟,何友,王国宏.测向交叉定位系统中的交会角研究[J].宇航学报,2005,26(3):282-286. XIU JIANJUAN,HE YOU,WANG GUOHONG.Study on cut angle of direction finding location system[J].Journal ofAstronautics,2005,26(3):282-286.(in Chinese)
[12]WANG G H,BAI J,HE Y,et al.Optimal deployment of multiple passive sensors in the sense of minimum concentration ellipse[J].IET Proceedings on Radar,Sonar&Navigation,2009,3(1):8-17.
[13]白晶,王国宏,王娜,等.测向交叉定位系统中的最优交会角研究[J].航空学报,2009,30(2):298-304. BAI JING,WANG GUOHONG,WANG NA,et al.Study on optimum cut angles in bearing-only location systems [J].Journal of Astronautics,2009,30(2):298-304.(in Chinese)
[14]王国宏,苏伟,白晶,等.不同量测误差情况下1D和2D被动传感器交叉定位系统最优交会角研究[J].电子学报,2009,37(6):1296-1299. WANG GUOHONG,SU WEI,BAI JING,et al.Study on optimal cut angle in 1D and 2D passive sensor triangulation with different measurement errors[J].Acta Electronica Sinica,2009,37(6):1296-1299.
[15]芦建辉,陈东锋,万朝江,等.主被动传感器实时信息融合的STMHM算法[J].电子学报,2012,40(9):1740-1745. LU JIANHUI,CHEN DONGFENG,WAN CHAOJIANG,et al.STMHM algorithm of active and passive sensors real-time data fusion[J].Acta Electronica Sinica,2012,40(9):1740-1745.(in Chinese)
[16]单甘霖,张子宁.面向目标跟踪的单平台主被动传感器长期调度[J].系统工程与电子技术,2014,36(3):458-463. SHAN GANLIN,ZHANG ZINING.Non-myopic sensor scheduling in a single platform for target tracking[J].Systems Engineering and Electronics,2014,36(3):458-463.(in Chinese)
[17]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].2版.北京:电子工业出版社,2009:83-85. HE YOU,XIU JIANJUAN,ZHANG JINGWEI,et al.Radar data processing with applications[M].2nded.Beijing:Publishing House of Electronics Industry,2009:83-85.(in Chinese)
[18]JULIER S J,UHLMAN J K.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Control,2000,45(3):477-482.
UT-DC Target Location Algorithm of with Active and Passive Sensors
WANG Guohong,SHENG Dan,YU Hongbo
(Institute of Information Fusion,NAAU,Yantai Shandong 264001,China)
Location fusion of the measurements of the active and passive sensors is highly nonlinear.The commonly used linear method,however,may lead to worse effect.Therefore,a fusion localization method based on the unscented transfor⁃mation(UT)and data compressing(DC)was proposed in this paper.Firstly,UT was taken to calculate the statistic charac⁃teristics of the two-dimensional variable,so as to eliminate the errors brought by nonlinear transformation.Secondly,since the angle measurement of the active sensor was also used in the triangulation location,the relativity between the active sen⁃sor location result and the triangulation location result was considered to improve the location precision.Theoretical analy⁃sis and simulation results showed that the location performance of the present method in this paper was superior to that of the traditional linear processing method.
active passive;passive sensor;nonlinearity;unscented transformation;relativity;data compressing
TN958.93
A
1673-1522(2015)05-0401-08
10.7682/j.issn.1673-1522.2015.05.001
2015-06-20;
2015-08-10
国家自然科学基金资助项目(61372027;61102165)
王国宏(1963-),男,教授,博士,博导。

