基于正交小波变换的目标检测方法

孙宏岩

（海军装备部航空技术保障部，北京100071）

基于正交小波变换的目标检测方法

孙宏岩

（海军装备部航空技术保障部，北京100071）

理论分析表明，独立高斯噪声经过正交小波变换后保持方差和独立性不变。基于Mallat的小波多分辨分析，通过对小波系数进行平方律处理，建立了基于正交小波变换的恒虚警率检测器模型，推导了相应的虚警和检测概率公式，分析了噪声未知情况下小波系数序列长度对检测性能的影响，并给出了合适的长度值。实验结果表明，所提出的检测器能满足不同虚警概率和杂波背景的要求，具有较好自适应性。

信号检测；正交小波变换；多分辨分析；高斯噪声

具有自动检测的智能化雷达是现代雷达的发展趋势，而自动检测过程的一个重要部分是恒虚警率（CFAR）处理[1-3]。CFAR设计的目的是提供相对来说可以避免噪声背景杂波和干扰变化影响的检测阈值，并且当与到达的样本进行比较时，使目标检测具有恒定的虚警概率。另一方面，自从Donoho提出基于小波变换的软阈值消噪方法[4]以来，小波变换在信号检测方面显示了巨大的潜力，至今已在信号分析、图像处理、量子力学、雷达、计算机分类与识别、数据压缩、边缘检测等方面得到了广泛的应用。传统的CFAR方法多在时域对信号进行处理[5-7]，关于频域CFAR处理也提出过一定的方法[8]。小波变换是一种时间窗和频率窗都可改变的时频局部分析方法，在处理非平稳信号方面有着独特的优势。针对雷达信号的非平稳性，研究小波域CFAR处理方法具有重要意义。

本文首先对含高斯噪声信号进行正交小波多尺度分析，基于高斯噪声在小波域中的特性，通过对小波系数进行平方律处理，建立了基于正交小波变换的恒虚警率（OW-CFAR）检测器模型，并给出了相应的虚警和检测概率公式，分析了信号小波系数序列长度对检测性能的影响。实验结果表明了该方法在不同虚警概率和杂波背景下的有效性和自适应性。

1 高斯噪声在正交小波域中的特性

离散小波变换（DWT）能用尺度函数ϕ(t)和小波函数ψ(t)的平移和伸缩形式来表示信号x(t)。对于给定的尺度函数及其对应的小波函数，它们应满足双尺度方程[9]：

式（1）、（2）中：h(n)和g(n)为多分辨分析中定义的共轭低通和高通滤波器的系数；t表示连续变量。

正交小波变换的h(n)还必须满足如下条件[10]：

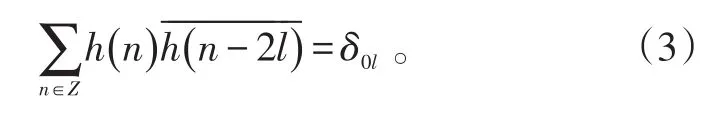
式（3）中：l表示非负整数；“-”表示取共轭，而h(n)与g(n)之间存在如下的对应关系：

以下用hn和gn表示h(n)和g(n)，则正交离散小波变换的多分辨分析可以表示为：

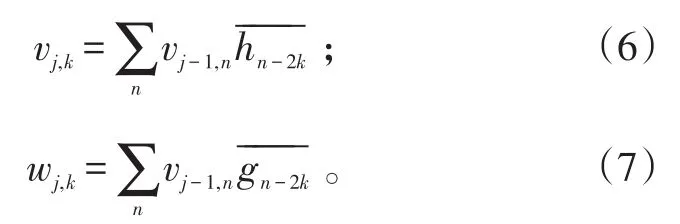
式（6）、（7）中：vj,k和wj,k分别表示尺度 j下平移位置k处的尺度系数和小波系数，较大的 j值对应于粗分辨尺度；v0,n表示原始的输入信号序列x(n)。

实际应用中，为了计算尺度系数和小波系数，一般采用Mallat算法[11]，其结构框图如图1所示。基于该算法，根据式（7）可以利用 j-1水平下的尺度系数vj-1，通过卷积获得 j水平下的小波系数wj，对所得系数进行基数为2的下采样最终获得小波系数。

图1 Mallat算法的框图Fig.1 Schematic of Mallat algorithm

为了进一步进行目标检测，首先分析独立高斯噪声经过正交小波变换后的特性。假设噪声序列N(n)是零均值方差为的独立高斯噪声采样值。若输入信号为{N(n)}，由式（7）知，尺度 j=1时的噪声小波系数表示为：

式中，上标N表示噪声。

噪声小波系数的均值为：

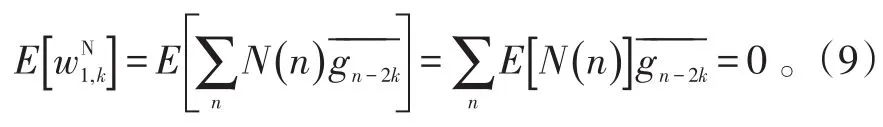
由于噪声是相互独立的，结合式（5）、（7）可知，在尺度j=1时的噪声小波系数的相关系数为：

式（10）中，n、m、l均为整数。

同理，由式（3）、（6）可知，尺度j=1时的尺度系数的相关系数为：

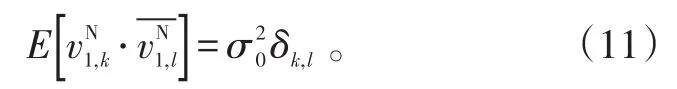
由式（10）、（11）的结论可知，基于Mallat的小波快速分解算法，利用式（6）、（7）进行迭代运算，所得的高斯噪声的小波系数依然是零均值方差为的独立高斯序列。

2 基于正交小波变换的检测器

本节给出了一种基于正交小波变换的OW-CFAR检测器：首先，将雷达回波信号经过正交小波变换，对尺度j下的小波系数进行平方律处理；然后，将所得结果进行OW-CFAR检测，超过检测门限的小波系数被认为是目标信号的小波系数，经过处理后加以保留，否则被认为是噪声的小波系数而被剔除；最后，对处理后的小波系数进行重构得到检测出的信号。

雷达信号X(n)一般有2个可能的分量[12]，即目标信号S(n)和杂噪信号N(n)。在有目标存在的条件下有

在无目标存在的条件下有

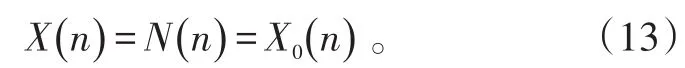
因此，X(n)可以被看作是来自于2个不同随机过程之一的样本函数[13]。其一表示目标不存在情况下的样本X0(n)；其二表示信号和噪声同时存在条件下的样本X1(n)。

由上一节的分析可知，独立高斯噪声经过离散正交小波变换后保持了原有的方差和独立性。因此，可以假设在一定的小波分解尺度 j下，回波信号的小波系数表示为：

式（14）、（15）中：H0表示无目标存在的假设；H1表示有目标存在的假设；和分别表示目标信号和噪声在尺度j下的小波系数。

在H0的假设下，λ′是总的背景杂噪平均功率水平，用μ表示；在H1的假设下，λ′是μ(1+λ)。其中，λ是目标与杂噪平均功率比。于是有：

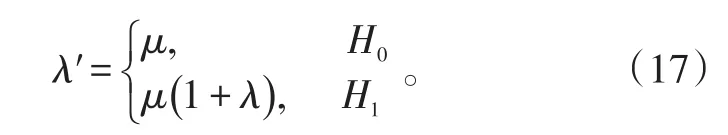
在均匀杂波背景中，参考单元采样是独立同分布的，且其对应的λ′均为μ。不失一般性，用Gk来表示，假设在尺度 j下小波系数序列长度为M，定义Sq为：

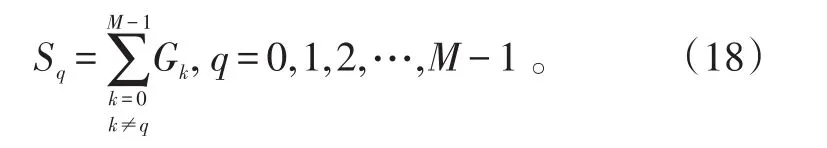
若在背景杂波功率水平μ确知的条件下进行最优检测，则只需要一个固定阈值Z0来判定目标是否存在，这时的虚警概率为：

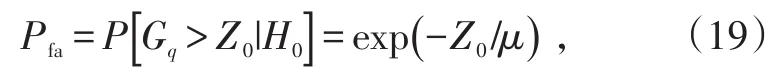
式中，Z0是固定的最优阈值。

最优检测的检测概率Pd为：

在背景杂波功率水平μ未知的情况下，由于阈值Zq=T⋅Sq是一个随机变量，因而可以用其统计特征将虚警概率表示为：

在第q个滤波器的输出端利用阈值Zq进行判决。在给定p0的条件下，可以得到标称化因子T。为了方便比较，这里保持虚警率恒定，即

式（22）中，PFA表示总的虚警概率。

将式（22）代入式（21）可以确定T。同理可得未知噪声功率水平下的检测概率PD为：

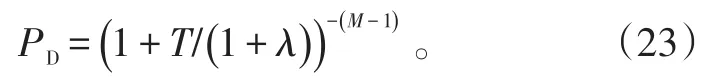
在噪声功率水平已知和未知2种情况下，分别利用式（19）、（20）和式（21）、（23），比较不同M值时二者的检测性能差异。假设2种情况的虚警概率相同，即

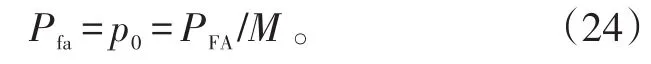
为方便比较，定义检测概率差值PDiff，它表征了在相同的虚警概率和输入信噪比条件下，噪声功率水平已知和未知时检测概率的差异大小，具体如下：

在尺度 j下，由式（18）、（21）可以确定阈值Zq=TSq，而小波阈值可确定为

根据式（26）所得阈值，可以利用Donoho的小波软阈值处理[4]方法：

3 仿真实验

利用上节提出的基于正交小波变换的OW-CFAR检测器，在噪声水平未知的情况下，对含高斯噪声的雷达回波信号进行检测。其中，目标信号S(n)为线性调频信号，原始含噪信号 X1(n)的信噪比为-0.108 6dB，信号长度为1 024，如图2所示。

图2 目标信号和高斯杂波背景下的信号Fig.2 Target signal and contaminated signal of Gaussian clutter

实验中，采用Matlab小波工具箱中的d6正交小波，分解层数为5，在不同虚警概率条件下，检测后的信号如图3所示，其中S2(n)、S4(n)和S6(n)分别是虚警概率PFA为10-2、10-4、10-6时的检测信号。可以看出，随着虚警概率的降低，检测信号中所含噪声分量越来越少，而且信号的高频细节信息也得到了较好的保留。

图3 高斯杂波背景下，不同虚警概率的检测信号Fig.3 Detected signals with different false alarm probabilities of Gaussian clutter

利用该算法对瑞利杂波和韦布尔杂波背景下的雷达回波信号进行处理[15]，原始信号X2(n)和X3(n)的检测前信噪比分别为-0.241 9dB和0.160 9dB，虚警概率PFA为10-2、10-4、10-6时的检测信号分别如图4、5所示。由图4、5中的处理结果可知，该检测算法在瑞利杂波和韦布尔杂波背景下仍能有效的检测信号，并较好的保留了细节信息，具有较好地鲁棒性和自适应特性。

图4 瑞利杂波背景下，不同虚警概率的检测信号Fig.4 Detected signals with different false alarm probabilities of Rayleigh clutter

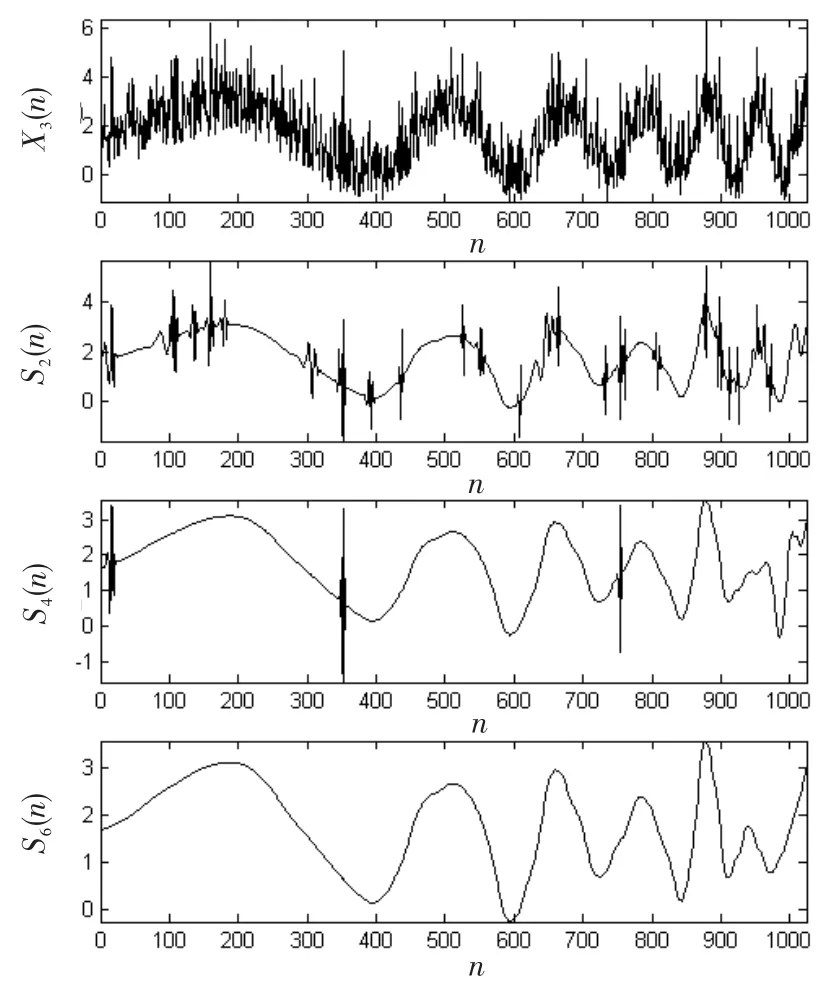
图5 韦布尔杂波背景下，不同虚警概率的检测信号Fig.5 Detected signals with different false alarm probabilities of Weibull clutter

4 结论

本文对信号小波域CFAR方法进行了初步的研究，由于独立高斯噪声经过正交小波变换后保持方差和独立性不变，在小波域中对小波系数进行平方律处理，接着建立小波域的OW-CFAR检测器模型，推导了相应的虚警概率和检测概率公式，比较了噪声未知情况下小波系数序列长度M对检测性能的影响，并给出了合适的M值。实验结果表明，基于小波变换的OWCFAR检测器在不同虚警概率条件下能有效的检测信号，具有较好的自适应性。

[1]HE Y，JIAN T，SU F，et al.Novel range-spread target detectors in non-Gaussian clutter[J].IEEE Transactions on Aerospace and Electronic Systems，2010，46（3）：1312-1328.

[2]JIAN T，HE Y，SU F，et al.Cascaded detector for rangespread target in non-Gaussian clutter[J].IEEE Transactions on Aerospace and Electronic Systems，2012，48（2）：1713-1725.

[3]HE Y，JIAN T，SU F，et al.Two adaptive detectors for range-spread targets in non-Gaussian clutter[J].Science China：Information Sciences，2011，54（2）：386-395.

[4]DONOHO D L.De-noising by Soft-thresholding[J]. IEEE Transactions on Information Theory，1995，41（3）：613-627.

[5]JIAN T，HE Y，SU F，et al.Adaptive detection of rangespread targets without secondary data in multichannel autoregressive process[J].Digital Signal Processing，2013，23（5）：1686-1694.

[6]JIAN T，HE Y，SU F，et al.Robust detector for rangespread target in non-Gaussian background[J].Journal of Systems Engineering and Electronics，2012，23（3）：355-363.

[7]JIAN T，HE Y，SU F，et al.Adaptive detection of sparsely distributed target in non-Gaussian clutter[J].IET Radar Sonar Navigation，2011，5（7）：780-787.

[8]WILLETT P，ZHEN WANG，STREIT R.Wavelets in the frequency domain for narrowband process detection[C]// IEEE International Conference on Acoustics，Speech，and Signal Processing.2001，5：3193-3196

[9]DAUBECHIES I.Ten lectures on wavelets[M]. Philadephia：SIAM，1992：12-26.

[10]程正兴.小波分析算法与应用[M].西安：西安交通大学出版社，1998：84-95. CHENG ZHENGXING.Wavelet analyses algorithms andapplication[M].Xi’an：Xi’an Jiaotong University Press，1998：84-95.（in Chinese）

[11]MALLAT S G.Multiresolution approximations and wavelet orthonormal bases of L2（R）[J].Transactions of the American Mathematical Society，1989，315（1）：68-87.

[12]JIAN T，HE Y，SU F，et al.Adaptive range-spread target detection based on modified generalised likelihood ratio test in non-Gaussian clutter[J].IET Radar Sonar Navigation，2011，5（9）：970-977.

[13]简涛，何友，苏峰，等.非高斯杂波下修正的SDD-GLRT距离扩展目标检测器[J].电子学报，2009，37（12）：2662-2667. JIAN TAO，HE YOU，SU FENG，et al.Modified SDDGLRT detector for range-spread targets in non-Gaussian clutter[J].Acta Electronica Sinica，2009，37（12）：2662-2667.（in Chinese）

[14]DILLARD G M，SUMMERS B F.Mean-level detection in the frequency domain[J].Radar，Sonar and Navigation，1996，143（5）：307-312.

[15]简涛，苏峰，何友，等.针对拖尾噪声的中值滤波—小波消噪算法分析[J].信号处理，2007，23（1）：79-82. JIAN TAO，SU FENG，HE YOU，et al.An algorithm analysis of median filter&wavelet threshold for heavy-tailed noise[J].Signal Processing，2007，23（1）：79-82.（in Chinese）.

Target Detecting Method Based on Orthogonal Wavelet Transform

SUN Hongyan
（Aviation Technology Support Branch of NED,Beijing 100071,China）

Theoretical analysis shows that independent Gaussian noises keep the independence and variance after the or⁃thogonal wavelet transform.Applying a squarer to the output of the wavelet transform,an OW-CAFR(orthogonal wavelet⁃constant false alarm rate)detector based on Mallat algorithm was proposed.The probability equations of false alarm and de⁃tection were also deduced.The influence of the length of wavelet coefficients on detection performance was analyzed,and the appropriate length was given.Finally,the experiment results of signal detection demonstrated that the proposed method could detect the targets under different false alarm rate and cluster background effectively,which showed the adaptability.

signal detectio;orthogonal wavelet transform;multiresolution analysis;Gaussian noise

TN957

A

1673-1522（2015）05-0414-05

10.7682/j.issn.1673-1522.2015.05.003

2015-06-20；

2015-08-07

孙宏岩（1962-），女，高工，大学。