关于凸函数单侧导数的连续性

张亚楠,　刘长剑

(苏州大学数学科学学院, 江苏苏州215006)

关于凸函数单侧导数的连续性

张亚楠,刘长剑

(苏州大学数学科学学院, 江苏苏州215006)

[摘要]证明了开区间上的凸函数其左导数必定左连续，右导数必定右连续.

[关键词]凸函数； 微积分基本定理； 单侧连续

在数学分析课程的教学过程中，对凸函数性质的介绍是一个重要的知识点. 一个简单而直观的例子是绝对值函数y=|x|. 容易验证它是凸函数, 其两个单侧导数存在并在x=0处间断.我们进一步观察发现，其单侧导数虽然在x=0处间断，但是分别单侧连续. 本文的主要目的就是将该结论推广到一般的凸函数上，即证明如下结论：

定理1设f(x)是定义在开区间I上的凸函数,则其左导数必定左连续，右导数必定右连续. 也即成立

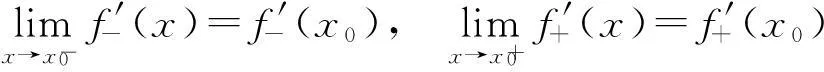
这个定理的结论与[1]中122页推论3(导数极限定理)很相似，但导数极限定理的证明需要拉格朗日中值定理，而对单侧导数而言拉格朗日中值定理不一定成立，所以定理1的证明需要新的方法.我们给出两种证明方法.方法一利用积分的思想而方法二则采用微分的思想.

引理1[3,4]设f(x)在开区间I上连续, 其单侧导数f′-或f′+存在且黎曼可积，则对∀a,b∈I，a≤b，成立

(1)

容易验证开区间上的凸函数满足引理1的条件，因此对凸函数成立(1)式.

定理1的证明(方法1)只证明定理的前半部分；后半部分可类似证明.

(2)

另一方面，由引理1可得

(3)

结合(2),(3)两式，即得结论.

以上是基于积分的证明，下面我们将给出一个基于微分的证明. 首先给出如下引理.

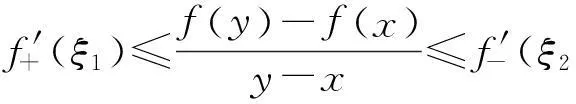
证只证明不等式的右半部分，左半部分类似可证.

任取z∈(x,y),由凸函数定义可知

若不然，则存在z∈(x,y),使得

记

F(ξ2)>F(y)-ε.

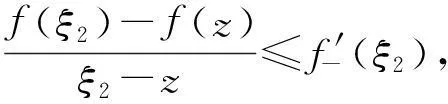
定理1的证明(方法2)同样只证明定理的前半部分；后半部分可类似证明.

由引理2 可知，∀Δx<0,∃ξ∈(x0+Δx,x0), 使得

上式中另Δx→0-, 即得

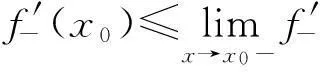
致谢：本文第一作者受到中国博士后基金(2014T70539)和教育部博士点基金(20133201120002)的资助，第二作者受到中国自然基金面上项目(NSFC-11371269)的资助.

[参考文献]

[1]华东师范大学数学系. 数学分析(上册)[M]. 3版. 北京：高等教育出版社，2001.

[2]谢惠民，恽自求，易法槐，钱定边. 数学分析习题课讲义[M]. 北京：高等教育出版社，2003.

[3]MichaelW.BotskoandRichardA.Gosser,StrongerVersionsoftheFundamentalTheoremofCalculus[J].TheAmericanMathematicalMonthly, 1986，93(4)：294-295.

[4]王良成.凸函数及其不等式[M]. 成都：四川大学出版社，2001.

OntheContinuityofOne-SidedDerivativeofConvexFunction

ZHANG Ya-nan,LIU Chang-jian

(SchoolofMathematicalSciences,SoochowUniversity,Suzhoujiangsu215006,China)

Abstract:Weprovethattheleftderivativeofaconvexfunctiononanopenintervalmustbeleftcontinuousandtherightderivativemustberightcontinuous.

Keywords:convexfunction;fundamentaltheoremofcalculus;one-sidedcontinuous

[基金项目]国家自然科学基金(11171342)；中央民族大学科研创新基金

[收稿日期]2015-01-11

[中图分类号]O178

[文献标识码]C

[文章编号]1672-1454(2015)04-0053-02