域同态的扩张的个数

高　升

(合肥工业大学数学学院，合肥230009)

域同态的扩张的个数

高升

(合肥工业大学数学学院，合肥230009)

[摘要]设h:F→Ω是域的同态，E是F的有限次扩域，本文讨论了使h到E上的扩张的个数取得最大值的条件.

[关键词]域； 单同态； 同态的扩张； 可分次数

1引言

设F是任意一个域，E是F的有限次扩域; h:F→Ω是从F到另一域Ω的单同态.本文主要讨论这样一个问题：有多少种方式将h扩张为从E到Ω的单同态？

为了简便，用记号Emb(E,Ω)表示从E到Ω的全部单同态的集合，用Emb(F,h)(E,Ω)表示所有扩张了h的、从E到Ω的单同态的集合，即

Emb(F,h)(E,Ω)={ξ∈Emb(E,Ω)|ξ|F=h}，

其中ξ|F表示ξ到F上的限制映射.这样，本文讨论的问题也就是集合Emb(F,h)(E,Ω)中元素的个数(在一般情况下，E和Ω之间没有包含关系，Emb(E,Ω)和Emb(F,h)(E,Ω)有可能为空集.)

将域扩张E/F的可分次数记为[E∶F]sep，则不等式

|Emb(F,h)(E,Ω)|≤[E∶F]sep

在任何情况下都是成立的(见本文引理5).

现有文献在某些情况下讨论了该不等式等号成立的条件.[1]第224页命题1证明了:当Ω是h(F)的代数闭包时，|Emb(F,h)(E,Ω)|可以取到最大值[E∶F]sep.[2]第20页命题3和[6]第77页定理16都证明了:当Ω是F的一个代数正规扩张且E是Ω/F的中间域时，从E到Ω的F-单同态的个数取到最大值[E∶F]sep.[4]第131页命题3.2给出了当Ω为F的扩域时使E到Ω的F-单同态个数等于[E∶F]的充要条件.[6]第79页推论1证明了：E的F-自同构群Gal(E/F)的阶一定不超过[E∶F]sep，且等式|Gal(E/F)|=[E∶F]sep成立的充要条件是E/F为正规扩张.[7]第142页定理5.2.6给出了当Ω为E在F上的正规闭包时使E到Ω的F-单同态个数等于[E∶F]的充要条件.文献[8]在第135页证明了，若F⊂E⊂Ω，则E到Ω的F-单同态个数一定不超过[E∶F]sep，在适当地选取Ω时可以取到最大值[E∶F]sep.

本文将在一般情况下讨论使|Emb(F,h)(E,Ω)|取到最大值[E∶F]sep的充分必要条件.

2对主要定理的叙述和证明

将有限次域扩张E/F的纯不可分次数记为[E∶F]ins，F在E中的可分闭包记为ES(此时有[E∶F]sep=[ES∶F]，[E∶F]ins=[E∶ES]).对于任一α∈E，用min(α,F)表示α在F上的极小多项式.F[X]表示F上的一元多项式环，以X为不定元.对于F[X]中的多项式

记号degf表示它的次数.对每一单同态h:F→Ω，定义一个映射

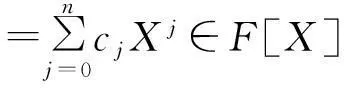
引理1([5, 推论5.2.9, 第218页])设F和Ω是两个域，h:F→Ω是从F到Ω的单同态，F(β)是F的一个单代数扩域， min(β,F)=f(X)，则

|Emb(F,h)(F(β),Ω)|=|{ω∈Ω|h*(f)(ω)=0}|，

即h到F(β)上的扩张的个数等于多项式h*(f)在Ω中的全部根的个数(不计重数).

引理2([3, 推论6.14，第287页])设F是一个域，f(X)是F[X]中的首一不可约多项式；L是F的一个扩域，使得f(X)在L[X]中可以完全分裂为一次因子的乘积.若f(X)在L中全部两两互异的根为γ1,γ2,…,γn，则必有n=[F(γ1)∶F]sep，且

f(X)=[(X-γ1)(X-γ2)·…·(X-γn)][F(α)∶F]ins，

即f(X)的每个根的重数都等于[F(γ1)∶F]ins.

引理3设E/F是域的纯不可分代数扩张，ξ1和ξ2都是从域E到域Ω的同态映射.如果ξ1|F=ξ2|F，那么必有ξ1=ξ2.

证若F的特征为0，则E/F同时又是可分扩张，从而必有E=F.故不妨设F的特征为素数p.此时，E和Ω的特征都是素数p.任取α∈E，则存在非负整数l，使得αpl∈F，从而有ξ1(αpl)=ξ2(αpl)，即ξ1(α)pl=ξ2(α)pl.所以，

[ξ1(α)-ξ2(α)]pl=ξ1(α)pl-ξ2(α)pl=0，

从而ξ1(α)=ξ2(α).

引理4设E=F(S)是域F的代数扩域，L是E/F的中间域；Ω是另一个域，h:F→Ω是从F到Ω的单同态.又设对每个α∈S，多项式h*(min(α,F))在Ω[X]中可完全分裂为一次因子的乘积.在这些条件下，如下结论成立：

(i) 集合Emb(F,h)(E,Ω)是非空的，即h可以提升为从E到Ω的单同态；

(ii) 对于每个ρ∈E，h*(min(ρ,F))在Ω[X]中可完全分裂为一次因子的乘积；

(iii) 若φ是从L到Ω的单同态且φ|F=h，则φ可提升为从E到Ω的单同态，即映射Emb(F,h)(E,Ω)→Emb(F,h)(L,Ω)(ξξ|L)是满的.

min(ρ,F)=(X-ρ1)(X-ρ2)…(X-ρk)，

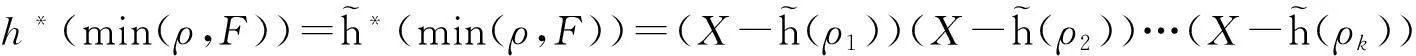
(iii) 此时E=L(S)，并且对每个α∈S，在L[X]中有min(α,L)|min(α,F).于是，在Ω[X]中有φ*(min(α,L))|φ*(min(α,F)).注意到min(α,F)的系数都属于F且φ|F=h，故

φ*(min(α,F))=h*(min(α,F)).

所以，在Ω[X]中有φ*(min(α,L))|h*(min(α,F)).由已知条件，h*(min(α,F))在Ω[X]中可完全分裂为一次因子的乘积，故φ*(min(α,L))在Ω[X]中可完全分裂为一次因子的乘积.于是，由本引理之(1)知，φ:L→Ω可提升为从E到Ω的单同态.

引理5设E/F是有限次的域扩张，h:F→Ω是从F到另一域Ω的单同态，则有

|Emb(F,h)(E,Ω)|≤[E∶F]sep.

证设ES为F在E中的可分闭包，则E/ES是纯不可分扩张，ES/F是单扩张.由于有限可分扩张必为单扩张，故可以选取β∈ES，使得ES=F(β).

设min(β,F)=f(X).若Emb(F,h)(E,Ω)=∅，则待证不等式显然成立.不妨设Emb(F,h)(E,Ω)≠∅.由引理3可知，映射

Emb(F,h)(E,Ω)→Emb(F,h)(ES,Ω)(ξξ|ES)

是单的，所以

|Emb(F,h)(E,Ω)|≤|Emb(F,h)(ES,Ω)|=|Emb(F,h)(F(β),Ω)|.

(1)

再由引理1可知，

|Emb(F,h)(F(β),Ω)|= |{ω∈Ω|h*(f)(ω)=0}|≤degh*(f)=degf=[F(β)∶F]=[ES∶F].

(2)

结合(1)式和(2)式，可知

|Emb(F,h)(E,Ω)|≤[ES∶F]=[E∶F]sep.

以下定理是本文的主要结果.

定理设E/F是有限次的域扩张，E=F(α1,α2,…,αr)，h:F→Ω是从域F到另一域Ω的单同态，则以下三者彼此等价：

(i) |Emb(F,h)(E,Ω)|=[E∶F]sep；

(ii) 对每个j∈{1,2,…,r}，多项式h*(min(αj,F))在Ω[X]中可完全分裂为一次因子的乘积；

(iii) 对每个ρ∈E，多项式h*(min(ρ,F))在Ω[X]中可完全分裂为一次因子的乘积.

证设ES为F在E中的可分闭包，则E/ES是纯不可分扩张，ES/F是单扩张.选取β∈ES，使得ES=F(β).设min(β,F)=f(X)(在以下的讨论中一直使用这些记号).

(i)(ii) 由于α1,α2,…,αr地位平等，只需证明：h*(min(α1,F))在Ω[X]中可以完全分裂为一次因子的乘积.

考虑映射λ:Emb(F,h)(E,Ω)→Emb(F,h)(F(α1),Ω)(ξξ|F(α1))，则有

Emb(F,h)(E,Ω)=∪h′∈Emb(F,h)(F(α1),Ω)λ-1(h′)=∪h′∈Emb(F,h)(F(α1),Ω){ξ∈Emb(F,h)(E,Ω)|ξ|F(α1)=h′}

=∪h′∈Emb(F,h)(F(α1),Ω){ξ∈Emb(E,Ω)|ξ|F(α1)=h′}=∪h′∈Emb(F,h)(F(α1),Ω)Emb(F(α1),h′)(E,Ω) .

此处，λ-1(h′)表示h′关于映射λ的全部原像的集合.集合Emb(F(α1),h′)(E,Ω)对于不同的h′是互不相交的，所以由引理5可知

|Emb(F,h)(E,Ω)|=∑h′∈Emb(F,h)(F(α1),Ω)|Emb(F(α1),h′)(E,Ω)|≤|Emb(F,h)(F(α1),Ω)|·[E∶F(α1)]sep.

又由(i)中条件，有

[E∶F]sep=|Emb(F,h)(E,Ω)|≤|Emb(F,h)(F(α1),Ω)|·[E∶F(α1)]sep，

所以

[F(α1)∶F]sep=[E∶F]sep/[E∶F(α1)]sep≤|Emb(F,h)(F(α1),Ω)|.

由引理5,又有

|Emb(F,h)(F(α1),Ω)|≤[F(α1)∶F]sep，

于是必有

|Emb(F,h)(F(α1),Ω)|=[F(α1)∶F]sep.

于是，由引理1可知，多项式h*(min(α1,F))在Ω中的根的个数(不计重数)恰为[F(α1)∶F]sep.又由引理2可知，min(α1,F)在任一分裂域中的全部根的个数(不计重数)为[F(α1)∶F]sep，从而h*(min(α1,F))在任一分裂域中的根的个数(不计重数)也是[F(α1)∶F]sep.由此可知， h*(min(α1,F))在Ω[X]中可以完全分裂为一次因子的乘积.

(ii)(iii) 这可由引理4(ii)直接推出.

(iii)(i) 由引理4(iii)可知，映射

Emb(F,h)(E,Ω)→Emb(F,h)(ES,Ω)(ξξ|ES)

是一个满射.由引理3可知，此映射同时也是一个单射.所以此映射是一个双射，从而有

|Emb(F,h)(E,Ω)|=|Emb(F,h)(ES,Ω)|=|Emb(F,h)(F(β),Ω)|

(a)

由引理1可知

|Emb(F,h)(F(β),Ω)|= |{ω∈Ω|h*(f)(ω)=0}|

(b)

由条件(iii)可知，多项式h*(f)=h*(min(β,F))在Ω[X]中可完全分裂为一次因子的乘积.因为β在F上是可分的，所以f(X)=min(β,F)在任一分裂域上都没有重根，从而

h*(f)=h*(min(β,F))

在Ω中没有重根.这样就有

|{ω∈Ω|h*(f)(ω)=0}|=degh*(f)=degf=[F(β)∶F]=[ES∶F]=[E∶F]sep

(c)

综合(a)，(b)，(c)三式，有

|Emb(F,h)(E,Ω)|=[E∶F]sep，

于是(i)得证.

3结论

现有文献对于使域嵌入的扩张的个数达到最大的充分条件多有讨论，本文的创新点在于证明了这些条件的必要性.

[参考文献]

[1]CohnPM.Algebra(Volume2)[M].Chichester·NewYork·Brisbane·Toronto:JohnWiley&SonsLtd, 1977.

[2]戴执中. 域论[M]. 北京：高等教育出版社，1990.

[3]HungerfordTW.Algebra[M].NewYork:Springer-Verlag,Inc, 1974.

[4]李克正. 抽象代数基础[M]. 北京:清华大学出版社, 2007.

[5]SahaiV,BistV.Algebra[M]. (英文第2版影印版). 北京：机械工业出版社，2008.

[6]ZariskiO,SamuelP.CommutativeAlgebra(Volume1)[M].NewJersey:D.VanNostrandCompany，Inc, 1958.

[7]张英伯，王恺顺. 代数学基础(下册)[M].北京:北京师范大学出版社, 2013.

[8]vanderWaerdenBL.Algebra(Volume1)[M]. (英文第7版影印版). 北京：世界图书出版公司，2007.

OntheNumberofExtensionsofaFieldHomomorphism

GAO Sheng

(SchoolofMathematics,HefeiUniversityofTechnology，Hefei230009,China)

Abstract:Leth:F→ΩbeafieldhomomorphismandEafinitedimensionalextensionfieldofF.Inthisarticle,wediscusstheconditionsforthenumberoftheextensionsofhtoEtoattainitsmaximum.

Keywords:field;monomorphism;extensionsofahomomorphism;separabledegree

[中图分类号]O153.4

[文献标识码]A

[文章编号]1672-1454(2015)04-0030-04