实验失败后的小组越野赛：北师大版数学六年级下册“圆锥的体积”教学设计与反思

实验失败后的小组越野赛——北师大版数学六年级下册“圆锥的体积”教学设计与反思

李智宏

广东省深圳市南山区同乐学校，深圳518000

一、学情分析

二、教学设想

三、课前准备

将学生分为6～8人一组，教师为每组准备足量的沙子，一个圆锥，四个圆柱，这四个圆柱分别与圆锥等底等高(1号)、等底不等高(2号)、等高不等底(3号)、高底都不等(4号)，每组规格不一样．每人一张过关地图，其中包含实验报告单，以及比赛得分说明．

四、课堂写真

(一)画面引入课题

师：大家现在的精神状态相当好！各加一分．

师：这节课老师和大家一起研究“体积”(板书)．我们已研究过这些物品的体积(边举手示意边说明)：土豆、红薯、石块、长方体、圆柱，回忆下用过了哪些方法？

生：土豆、红薯、石块这些属于不规则的物体，不能量出有效数据，所以对于这类物体的体积，我们是将它们放入装水的量杯中，看水增高了多少从而来推断它们的体积是多少．而长方体、圆柱是规则物体，将长方体切成1立方厘米的小块能推出长方体的体积公式；将圆柱沿着底面半径切开，然后拼成一个类似长方体的物体，可以推出圆柱的体积公式．

师(板书：切拼、水量)：那么，圆锥也是一个规则物体，能不能也找到它的体积计算方法呢？

生：我们可不可以也像圆柱那样用切拼的方法呢？

师：老师也想到了“切拼”方法，还做过这个实验，让我们来看看这段视频．

微课视频演示：将圆锥等分成若干小块，以各种方式努力地去拼成以往学过的规则图形，均以失败告终．

师：看来，需要另辟蹊径，找到另外的方法来研究“圆锥的体积” (板书课题)．

【设计意图:荷兰数学教育家弗赖登塔尔说过：真正的数学家——常常凭借数学的直觉思维做出各种猜想，然后加以证实．学习本课之前学生已经有了“圆面积的推导”及“圆柱体积公式的推导”这两个学习经验，学生很容易将“切拼”的方法迁移到这节课的学习过程当中．考虑到学生的动手能力及课堂时间的限制，不可能在一节课中完成两个实验，放弃这个想法，学生会心有不甘．而微课的短小精悍正好解决这一矛盾：1分钟的视频展示不仅吸引了学生的注意力，更满足了学生的好奇心，顺利进入下一个实验．

同时，本环节也向学生说明这样一种思想：相对于不规则的物体，规则物体是可以得出公式并计算的．】

(二)猜想实验汇报

1.师：我们今天的学习分小组进行闯关越野赛，好吗？让我们先看看课堂学习比赛过关图，分为四关：问题猜想—实验验证—辨别真伪—实际应用．比赛可以开始了吗？好！第一关——问题猜想，请看清楚地图上的两个问题，2分钟的组内思考讨论时间．任务开始！

课件呈现猜想：

(1)圆锥与我们认识的哪种立体图形的关系最为密切？它们之间有哪些共同点？

(2)你准备怎么来验证你的猜想？

学生边思考、边讨论，并在过关图上作简单的记录．

师：时间到！请各小组派代表向大家说说你们的想法．

生：我认为圆锥的体积应该和我们以前学过的圆柱的体积有很密切的关系．它们的共同点是底面都是圆的．我们小组准备用圆锥装满沙子往圆柱里面倒，从而比较它们的大小关系．

【设计意图：用比赛的方式可以激发学生的挑战欲望，还可以提高课堂效率．教师课前设计好本课的过关地图，上课带领学生读一读，能让学生明确本节课的内容及努力的方向；以分组的形式学习，让个别学生对即将发生的学习减少顾虑，不胆怯；同时这两项安排让全组学生特别是组长在心理和行动上作好充足的应对准备．】

2.师：我们的猜想是否行得通？让我们进入第二关——实验验证．用我们手上的工具来验证我们的想法．12分钟的实验及准备时间．请大家严格按照实验要求进行操作．(念要求)任务开始！

(1)实验要求：①将圆锥装满沙后，用尺子或笔等工具将杯口的沙抹平；②要将圆柱装满；③完成实验报告单；④将组内实验数据填写在教室计算机相应的表格中．

课件呈现表格：

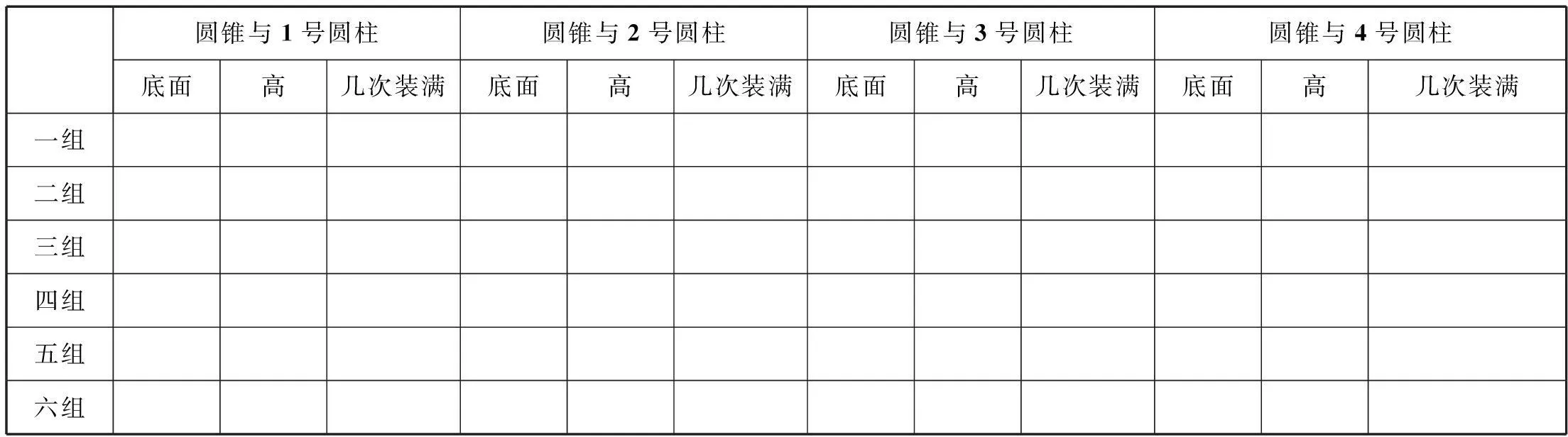
圆锥与1号圆柱圆锥与2号圆柱圆锥与3号圆柱圆锥与4号圆柱底面高几次装满底面高几次装满底面高几次装满底面高几次装满一组二组三组四组五组六组

师：时间到！六个小组的任务全部完成，下面老师开始检测．仔细观察全部小组的实验数据，你有什么发现？

生：我发现一个特殊情况，在1号圆柱那一栏，差不多都是3次．

师：为什么是“差不多”？

生：可能是装沙子的时候会有误差吧？有的组装得满些，有的组装得浅些．所以会出现比3次多一点或者少一点的情况．

师：有道理！那为什么都差不多是3次呢？会不会每组圆柱和圆锥都是一样大的，请小组长举起来让大家看看．

生：有的组大一些，有的组小一些，说明在等底等高的情况下，大号的也是3倍的关系，小号的也是3倍的关系．

师：大家说得挺好的，让我们再看看另外三种实验数据．

生：另外三种情况数据相差比较大，找不出任何规律．

师(指着最大的和最小的两个数)：这两个数据是哪两个组得出的，也举起对应的圆锥和圆柱给大家看看．

生：圆锥和圆柱的体积看起来相差特别大的，数据就很大，体积看起来相差不大的，得出来的数据就比较小．

师：从以上讨论你们有什么发现？

生：等底等高的圆柱．

师板书，追问：为什么要加“等底等高”？

生：从实验来看，不是所有情况下的圆柱和圆锥都是3倍的关系．

(2)在这个结论或公式中，你想提醒大家注意些什么？

师：能把你觉得需要注意的地方再清楚地说一遍吗？还有什么疑问或者想法吗？

生：我想提醒大家的是：要计算圆锥的体积，一定有“等底等高”这个前提条件．

生：我有个疑问：有没有可能，不在等底等高的情况下出现3次装满这样的情况？

生：我觉得有可能，但这只能是碰巧，概率很小．

师：同学们说得都非常精彩！我们这个结论只限于一般的情况，即只讨论“等底等高” 的情况，而这种小概率事件我们不讨论．

(3)师：大家通过实验都得出了圆锥体积公式，如果用V表示圆锥的体积，用S表示底面积，用h表示高，你能写出圆锥的体积公式吗？

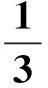
生：那就是圆柱的体积了．

师：看得出来，大家都对刚才的实验很有成就感！让我们看着屏幕回顾一下刚才的实验过程．当时的数学家为了找到圆锥的体积公式，也用了刚才的方法．刘徽，魏晋时期杰出的数学家，他发现了圆柱、圆锥、圆台等体积公式．其实我们刚才的实验过程正是经历了数学的再创造．老师为你们感到自豪！(竖拇指)

【设计意图：将猜想与实验分开，利于小组之间的互相借鉴及改进，明确实验的方向，减少失败的成本，提高对实验的信心；带领学生齐读实验要求及温馨提示，能让学生了解即将进行的实验动作，以便快速进行组内的分工安排，并在指定的时间内完成实验任务．

教师为每组准备的学具大小各不相同，每组的学具有五样，一个圆锥，另外四个是圆柱，分别与圆锥等底等高、等底不等高、等高不等底、高底都不等．实验完毕各小组根据实验的快慢在班级计算机上输入自己的实验数据，再组织学生进行分析讨论．这样安排的目的是为了让学生感受实验数据的随机性，发现在这些看似纷繁复杂的数据中得出的结论却是唯一的，验证了实验方法的正确．让学生感受到实验的奇妙，体验到成功的喜悦．

得出实验结论后，又用课件重现实验过程，以便帮学生梳理、明晰思路，加深印象．这个环节的最后安排了刘徽的故事，让学生与古代的数学家走在了一起，在感受民族自豪感的同时再次体验成功是非常简单的一件事情，加强了学生对数学学习的自信心．】

(三)实践检验解题

1.师：接下来进入第三关——辨别真伪，请做好抢答准备．

选择并说明理由．(听口令抢答)

(1)圆柱的体积相当于圆锥体积的()．

生：只有在“等底等高”的情况下，圆柱的体积是圆锥体积的3倍．所以这题是不确定的．

(2)一个圆柱与一个圆锥等底等高，圆锥的体积是6m3，则圆柱的体积是()．

A.6m3B.18m3C.2m3

生：这题选B，用6×3=18m3．

师：为什么这样想呢？

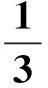
(3)一个圆柱与一个圆锥等底等高，圆柱的体积是6m3，则圆锥的体积是()．

A.6m3B.18m3C.2m3

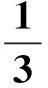
(4)一个圆柱体积是6m3，把它削成一个最大的圆锥，削去部分是()．

A.6m3B.4m3C.2m3

师：你怎么知道是与圆柱等底等高呢？

生：因为题目要求圆锥“最大”，说明底和高都不能变，所以与圆柱等底等高．

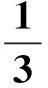
2.师：那就让我们进入实战阶段：第四关——实际应用．可向组内成员请教，5分钟时间，任务开始！

(1)独立练习课本“练一练”第1题．(求下面圆锥的体积)

(2)农民伯伯量得他的圆锥形小麦堆的底面周长是12.56米，高为1.5米，如果每立方米小麦是800千克，那么这堆小麦有多少千克？

师：任务全部完成！教师来检查一个小组的答案．(实物投影)

学生汇报时，老师要求学生说明理由：第1题的第1小题告诉了底面积和高，直接代入公式计算；第2小题要通过半径算出底面积再计算体积；第3小题要先根据直径得出半径，再通过半径计算底面积，从而通过公式得出体积．

师：我们已经能根据具体数据计算圆锥的体积，(师随手拿起某小组的圆锥)要计算这个圆锥的体积，需要知道或者量出哪些数据？

生：知道圆锥的底面积和高的数据就可以进行计算了．

生：量出圆锥的底面半径和高的长度也可以求出圆锥的体积．

生：量出圆锥的底面直径和高或者底面周长和高，都可以求出圆锥的体积．

【设计意图：此环节从练习到“教师随手拿起圆锥提问”都是为了一个主题：计算圆锥的体积，需要量出哪些数据？因为是第一节课，不需要技巧性或较复杂的练习，所以整个练习都围绕这个最基本的问题从不同的侧面来设计：练习题只有一道题可以直接套公式做出，其余的题虽说也要根据公式来做，但要“跳一跳才能摘到果子”，让每个学生对新知识的学习既有成功的喜悦又有挑战乐趣；“教师随手拿起某小组的圆锥”，动作看似随意，实质是告诉学生接下来的问题是针对任意一个圆锥而提出的，同时教师的这个提问也是对应用练习的一个小结．】

(四)游戏巩固拓展

我们的过关比赛到此结束，谁是今天的比赛冠军呢？让我们看看小组的最后得分，恭喜××小组，掌声祝贺！

师：接下来是我们的娱乐时间．你们猜这三杯诱人的饮料是否相等？(播放三杯饮料相等的动画)除了用倒入量杯这种方法来验证三杯饮料相等，是不是还可以用捏橡皮泥的方法来验证呢？一起来玩玩吧．

五、教学反思

关于这节课，教师做了大量的准备工作：设计微课、导学案、过关地图、板书、六套数据不同的柱体与锥体、过关说明、得分规则等，也确实收到了非常好的效果．

1.“微课”及“越野赛” 的引入在满足学生的好奇心之后，他们的情绪空前高涨．整堂课的过关任务分成抢答与按时答题两种形式，根据题目内容的难易及照顾学生的体力交错进行，学习气氛热烈、紧张、有序．最大限度地调动了全体学生的参与性，从练习检测结果及随意抽取的学生回答情况来看，比预先设计的要达成的学习目标的完成还要好．

2.利用课件的优势，将全班的实验数据统一填写在大屏幕的表格中，弥补了数据的单一性，打消了学生心中的不确定性，从而能全面、准确并肯定自己得到的实验结论．同时组内合作相同的实验，既节省时间，也帮助那些动手能力弱的学生见证了实验的全过程，从而达到对实验结论的真正理解与掌握．

众所周知，竞赛的形式往往目的性太强，本节课虽有所考虑，但也不可避免地在这方面出现了缺憾．

由于竞争对速度的要求，小组里每个成员都将绝大部分精力用于追求正确答案、带动组类比较弱的同学、忙于承接下一个学习任务，导致学生没有充分的时间去思考、消化、回味，因此本节课堂没有让人特别欣喜的生成；同时学习能力较弱的同学是否真的在组内同学的辅导下学会也让人质疑，或许囫囵吞枣，或许依葫芦画瓢．因此，如何在“越野赛”课堂里产生更加精彩绝伦的智慧以及如何对差生进行更好的评价都将是笔者在以后的教学中需要思考的．