高三化学复习教学中学生试题解答错误的处理

高三化学复习教学中学生试题解答错误的处理

黎绍亮

(安徽省阜阳市第五中学，阜阳236000)

【摘要】高三化学复习教学中教师经常面临课堂评析试卷.如何处理学生试题的解答错误，本文提出了模型扩展法、点盲规范法、内隐分解法三种有效方法.

【关键词】复习教学解答错误模型扩展法点盲规范法内隐分解法

皮亚杰说：“学习就是一个不断犯错误的过程，同时又是一个不断通过反复思考、挖掘错误缘由，并逐渐消除错误的过程．”高三复习中，教师经常面临考后阅卷和课堂评卷，如何处理学生试题的解答错误，即科学控制纠错过程中的变量就显得至关重要．

教师处理学生的试题解答错误，主要是控制两个变量，一个变量是学习客体，即影响学生错误解答的最核心因素．在化学学科的学习中，化学基本概念和基本原理以及化学事实、化学语言构成了化学学科的核心知识和能力，而化学观念具体表现为个体主动运用化学思想方法认识身边事物和处理问题的自觉意识或思维习惯[1]．因此纠错必须首先从学生的化学观念重构入手，接着考虑学生对概念原理的准确理解，最后再关注学生记忆的化学事实、化学语言；另一个变量是学习时间，即教师与学生一起纠错的时间，显然课堂是主战场，其次是课余时间．

根据以上分析，笔者认为，教师可以在错题分类的基础上，设计出解决不同类型错误的针对性方案，并辅以适当教与学策略，比如化学观念、概念原理可采用课堂模型扩展法，化学事实、化学语言可采用课堂点盲规范法，这样可使学生在今后的学习中不再出现同类型错误，或帮助学生实现同类型错误出现概率较大程度地降低．

一、课堂模型扩展法

1．从化学观念入手

在化学教学中实施“观念建构”的教学，有利于增进学生对知识的深刻理解和促进学生科学素养的全面发展；学生只有将化学观念内化为自身学习化学的行为准则和活动样式，才可真正达到“高屋建瓴”的理解境界．对于那些化学观念融合型试题，教师可以通过化学观念解读，帮助学生构建化学观念融合模型、实现扩展学习．

【错误案例1】写出0.08 mol氯气通入到0.1 mol溴化亚铁溶液中的离子方程式，并描述实验现象．

2.从概念原理入手

化学基本概念和基本原理因其具有抽象性、概括性、逻辑性、思想性、解释性和预见性等诸多特点，一直是化学学科的重要内容．基本概念是思维的“细胞”，是组成其他思维形式的基本要素；基本原理是思维的“器官”，是体现整体有序思维的重要表达形式．因此，学生对基本概念和基本原理的知识构建就是形成一种高度概括，达到自我主动认识规律、归纳内容、迁移运用，进而认识到事物本质．[2][3][4][5]特别需要强调的是，高三复习中有关考查基本概念和基本原理的试题，一个最重要的功能就是培养学生特有的化学学科思维能力；而教师帮助学生锤炼思维过程和对相关知识的概括、解释能力，即通过课堂试卷评析中，形成“错一题，备一类”，实现对点的基本理解，再由点到线、由线到面，达到事半功倍的纠错效果．其中热化学方程式书写、电化学、化学平衡、盐类水解等有关试题及其错误解答就具有这样的功效．

A．增加CO浓度 B．降低温度

C．增大压强 D．减少水蒸气

【基本概念和基本原理解读】化学平衡属于化学热力学范畴的基本概念，化学平衡状态既是某种状态，也是某种状态的延续过程；化学平衡移动则属于过程性问题，又隶属于基本原理．因此，教学要遵循由点开始、再从点到线、从线到面的纠错展开方式，帮助学生建立基于该基本原理的学科思维模型，引导学生形成相应的整体性认识．

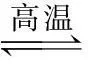
第一步：构建t2时刻的学科思维模型，实现对点的科学理解．

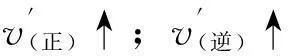
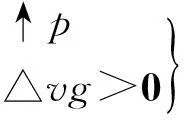
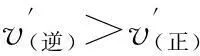
[说明] “↑”表示增大或升高；“←”表示可逆反应向逆向移动；“∈”表示属于；“”表示推导出；“⟺”表示等价于．

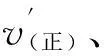
第二步：拓展探究，构建一类的学科思维模型，实现从点到线．

第三步：创新说明，构建高考试题新变化趋势的学科思维模型，实现从线到面．

根据拓展探究得出的一类学科思维模型——十五种化学平衡移动图像中的任何一种，还可以采用思维减法处理，要么减去正反应速率的变化曲线，要么减去逆反应速率的变化曲线，从而实现由双组曲线型向单组曲线型转化；也可以采用思维加法处理，由不确定的某一反应物或生成物反应速率化学平衡移动图像具体到某三到四个反应物或生成物相关的变化曲线，从而实现由双组曲线型向复合组曲线型转化．

二、课堂点盲规范法

考试完毕，学生在自我整理和分析错题时，还有不少是由于化学事实、化学语言、化学思维起点和切入点的盲点引起的，因此教师在课堂纠错的关键在于点出对应盲点，做到帮助学生规范认识，并寻找到有效的记忆方法．

1.关于化学事实解答错误

高中阶段一方面需要理解并掌握许多物质性质、化学变化进程和结果、基本实验操作和实验过程等化学实验事实，比如浓盐酸、浓硫酸、浓硝酸在发生化学反应时，一定发生浓度减小，因此就有浓盐酸与二氧化锰共热制取氯气、浓硫酸与铜共热反应而不能完全进行到底出现酸过量的事实，浓硝酸与铜反应生成的产物要发生变化的事实：起初生成二氧化氮，后来转化为一氧化氮；另一方面要正确理解氧化还原反应、化学反应中的能量变化、化学反应的速率和限度、电解质在水溶液中的行为等化学理论事实．比如碳酸根离子遇到铵根离子会发生相互促进水解是事实，同时二者与水解微粒主体比较，其最终的水解程度依然偏小，还要承认二者可以在水溶液中大量共存的事实，即存在碳酸铵溶液．因此对于高考模拟训练试题中的此类错误，必须明确提醒学生充分尊重化学事实．

需要提别指出的是，许多化学基础知识，学生需要作适当记忆，不论是布鲁尔的有意义记忆，还是简单机械记忆，必须强化记忆．教师对有些试题的错误解答必须帮助学生明确相关化学知识缺陷；同时在课堂上找到解决这些化学知识记忆、理解的共性新突破办法；另外在课后还要尽量个别辅导，争取用个性化方案实现突破．比如物质的物理性质、化学性质、用途以及与之有关的基本实验，可以用元素观统领法进行集中理解记忆，也可以采用分散突破法逐一记忆．

2.关于化学用语解答错误

化学方程式的书写、根据题意书写离子型氧化还原反应、元素在元素周期表中的位置描述、电子式的书写等化学用语，是试题经常考查的内容．学生在回答相关问题时，可能会写出千奇百怪的错误形式．教师如果在课堂上宣讲某些错误形式，就会有少数学生下次出现教师提醒的那些错误，因为这些学生往往会在思想不集中的情况下获得它们．笔者在教学实践中通过比较后发现，强调它们的规范书写或按照书写规则再次板演示范，纠错效果通常会更好．

3.关于思维起点和切入点错误

近几年高考试题，尤其是新课程高考试题，逐步由知识型向能力型、由暴露型向潜隐型、由单一型向综合型的方向发展．有些学生审题过程中经常存在不能看清定语或宾语等外显条件．比如，有些同学会将电子数目、电子物质的量混为一谈；也有些学生不善于挖掘题目的隐含条件，造成答题错误．

此时，教师点评试卷既要尽可能增加学生自我发现盲点、纠正错误的机会，更要帮助他们养成科学避免盲点、严谨治学的态度．特别要加强学生处理这些试题的科学方法指导：要帮助他们学会寻找思维起点的最佳途径——对试题进行边读边标注，画圈或画线来表达出定语和宾语等的不同，做到有针对性地回答；也要力争帮助学生找到科学把握思维切入点的方法——督促他们养成边读、边思、边写的习惯，如挖掘试题中化学概念、化学反应、数值特征、物质组成、物质性质、反应特征和实验现象等隐含条件[6]；区分定性问题、半定量问题和定量问题；把重点、难点、易错点、易混点写出来，甚至把考点知识结构图画出来、把答题灵感记下来；如果有必要，还可以让每位学生建立个性化的“思维起点和切入点的盲点”题库．

三、课堂内隐分解法

当然，教师也不能有错必宣．实际上有些错误，既不具有班级整体代表性，也不具有典型性，仅是班级某一位学生或极少数学生在某个问题上的极特殊错误．此时，教师需要把这些错误在课堂内作艺术性地淡化、隐藏，即只利用课余时间分解错误，避免由于宣讲错误而造成对班级全体学生的不良影响．

1.关于个性化偏差错误

化学知识在被建构的过程中，每位学生都可能对不同的知识点产生自我理解偏差．因此，这些个性化错误，属于非班级普遍性的、非经典性的错误，它们可能是关于化学观念建构型错误，也可能是化学基本概念和基本原理理解错误，也可能是化学事实、化学语言记忆不准确等．诸如此类天马行空的错误解答，不适合课堂举例展示，教师最好利用课余时间与这些学生面对面探询、辩驳、讨论，在调查清楚这些错误解答的缘由后，再进行相关知识更正、辨析，最后帮助学生实现认识纠偏．

2.关于个性化偏正“错误”

还有一些优秀学生，由于参加了化学奥林匹克竞赛和化学自主招生相关课外学习，自己储备了丰富的大学化学知识；由于参加生物、物理、数学等奥林匹克竞赛和自主招生相关课外学习，自己储备了这些相关学科的丰富知识，他们会出现一些化学学术前沿知识和学科交叉知识的偏正理解．但是局限于中学阶段的基础知识现状，这些解答往往与试题的参考答案相悖而被定性为错误，因此本文把这些定义为偏正“错误”．为避免挫伤这些学生追求学术的积极性，教师不但不能在课堂上公开批评，也不应该简单宣布参考答案了事．教师同样要通过课余时间积极了解他们，在知晓他们的认识方法、分析思路后，再查阅相关内容资料，和他们作及时、真诚、有意义的交流，帮助他们学会正确处理当前高考要求和未来学术研究的区别．

参考文献

[1]毕华林,卢巍．化学基本观念的内涵及其教学价值[J]．中学化学教学参考,2011(6):3-6．

[2]宫凯峰． 概念原理探微[J]．长春师范学院学报,2011(01):78-79．

[3]吴俊明,王祖浩．化学教学论[M]．南宁：广西教育出版社：102-110．

[4]韩秋萍,魏壮伟．基于化学概念原理的科学本质教学模式初探[J]．教学与管理，2011(21)：151-152．

[5]蓝文平．概念原理内容教学的策略和方法及问题讨论[J]．吉林教育,2010(10):3．

[6]李召亮,孙中林．化学试题中隐含条件的挖掘途径[J]．数理化学习(高中版),2002(21)：49-51．