剖面平面图反算数据的实现
毕 武 袁小龙 段新力 黄显义 彭仲秋 向诗强 张 恒(①新疆地矿局物化探大队昌吉831100②乌鲁木齐金维图文信息科技有限公司乌鲁木齐830091)
剖面平面图反算数据的实现
毕 武 袁小龙 段新力 黄显义 彭仲秋 向诗强 张 恒
(①新疆地矿局物化探大队昌吉831100②乌鲁木齐金维图文信息科技有限公司乌鲁木齐830091)
为了获取矢量图件上剖面平面图的数据,可以将剖面平面图线文件分解成基线和剖面线,根据数据比例尺、成图比例尺等参数及线段相交原理,将原始数据反算出来。本文主要介绍了线段相交原理在剖面平面图反算原始数据中的应用,并编程实现了该方法,给出了实例。
剖面平面图矢量化数字化线段相交。
1 引言
在航磁数据库建库工作中,接触的原始资料很大一部分是记录在厘米纸上的剖面曲线,早期的工作是利用CAD软件和数字化仪,分别输入剖面基线和剖面曲线,然后进行计算处理得到剖面数据坐标和值,其数字化精度常因不同的人操作而出现人为误差,所以一般是采用两个人分别数字化后,再取平均值的方式处理,这样既费时又效率不高。特别是对现在的大比例尺磁测剖面平面图,剖面线交错密集,如果仍用以上方法数字化,将是一项很复杂的工作。本文作者采用MAPGIS进行剖面图矢量化,利用Qt Designer这一跨平台图形工具包和Fortran编程语言,反算出数据和坐标,实现了剖面图数字化程序的开发,集成在GeoIPAS V2.8系统中。程序操作简单、方便、实用,生成的数据结果与原测数据吻合度好。
2 算法模型
《地理信息系统算法基础》[1]第24页,算法二。
定义A、B、C、D为二维空间的点,则有向线段AB和CD的参数方程为:
AB=A+r(B-A),r∈[0,1],CD=C+s(D-C),s∈[0,1]
如果AB和CD相交,则:
A+r(B-A)=C+s(D-C)=>Ax+r(Bx-Ax)=Cx+s(Dx-Cx)
Ay+r(By-Ay)=Cy+s(Dy-Cy),r,s∈[0,1]
解方程,求r和s:
r=((Ay-Cy)(Dx-Cx)-(Ax-Cx)(Dy-Cy))∕((Bx-Ax) (Dy-Cy)-(By-Ay)(Dx-Cx))
s=((Ay-Cy)(Bx-Ax)-(Ax-Cx)(By-Ay))∕((Bx-Ax) (Dy-Cy)-(By-Ay)(Dx-Cx))
设P为直线AB和CD的交点,则:
P=A+r(B-A)=>Px=Ax+r(Bx-Ax),Py=Ay+r(By-Ay)
如果(0≤r≤1)and(0≤s≤1),则有向线段AB和CD的交点存在,否则交点不存在。
如果(Bx-Ax)(Dy-Cy)-(By-Ay)(Dx-Cx)为0,则AB和CD平行。
如果(Ay-Cy)(Dx-Cx)-(Ax-Cx)(Dy-Cx)为0,则AB和CD共线。
如果直线AB和CD相交,而交点不位于线段AB和CD之间,则交点位置可以通过如下条件判断:
如果r>1,则P位于有向线段AB的延长线上;
如果r<0,则P位于有向线段BA的延长线上;
如果s>1,则P位于有向线段CD的延长线上;
如果s<0,则P位于有向线段DC的延长线上。
3 功能设置
程序主要功能,见图1:
⑴按输入线顺序对应:基线和剖面线的明码文件是一一对应的,即可以按输入顺序来进行转换;
⑵按属性顺序对应:根据两个属性文件的编号来进行对应,这种情况适用于当在MAPGIS编制图时,基线和剖面线没有按照一定顺序输入时,就需要使用属性文件来进行对应;
⑶图幅比例尺:剖面图成图比例;
⑷数据比例尺:剖面线纵向的显示比例;
⑸方位角选择:在计算的过程中,可以根据剖面线的角度来进行值的运算;
⑹正负值镜像:如果计算结果与实际正负值相反,可选择镜像选项改正。
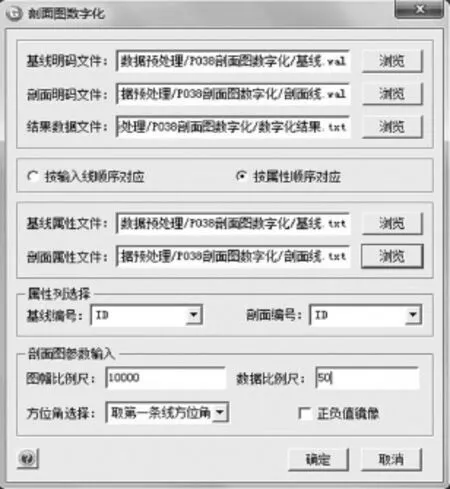
图1 剖面图数字化界面
4 程序实现
一个完整的计算过程为:剖面图数字化→转为明码文件→输入剖面基线明码文件→输入剖面线明码文件→输入基线属性文件→输入剖面线属性文件→输入保存结果文件名→输入剖面图参数→计算输出数字化剖面数据文本结果。
剖面图参数包括:成图比例尺、数据比例尺、剖面方位角的选择。剖面方位角考虑了航测和地面测量的多种情况,如果剖面线为统一的方位角,就选择取“第一条线方位角”;如果各剖面线方位角稍有变化,还可以选择“取所有线的平均值”;对于一个工区如果设计了多个方位角或者环形方位角的情况,还可以选择按“每条线取方位角”。
程序计算如下:
!基线点和剖面点不相等,计算基线的方位角:
do 500 i=1,nline-1
if(iselectline.eq.2)then
fwj=atan((y1(i,1)-y1(i,n1(i)))∕(x1(i,1)-x1(i,n1(i))))
else
endif
!循环计算,先判断过剖面线上每个点的垂直基线的线与基线是否相交,如果相交,再计算交点坐标:
do 600 j=1,n2(i)
!直线CD(xc,yc,xd,yd)是以垂直基线且过剖面线上的点的直线:
xc=x2(i,j)-zmax*cos(fwj+pi∕2.0)
yc=y2(i,j)-zmax*sin(fwj+pi∕2.0)
xd=x2(i,j)+zmax*cos(fwj+pi∕2.0)
yd=y2(i,j)+zmax*sin(fwj+pi∕2.0)
do 700 j1=2,n1(i)
xa=x1(i,j1-1)
ya=y1(i,j1-1)
xb=x1(i,j1)
yb=y1(i,j1)
st=(xb-xa)*(yc-yd)-(xc-xd)*(yb-ya)
t=((xc-xa)*(yc-yd)-(xc-xd)*(yc-ya))∕st
s=((xb-xa)*(yc-ya)-(xc-xa)*(yb-ya))∕st
if(s.ge.0.and.s.le.1.and.t.ge.0.and.t.le.1)then
isEmpty(i,j)=1
x3(i,j)=xa+t*(xb-xa)
y3(i,j)=ya+t*(yb-ya)
dx=x2(i,j)-x3(i,j)
dy=y2(i,j)-y3(i,j)
dxy=sqrt(dx*dx+dy*dy)
if(dxy.gt.0.0001)then
if(dy.gt.0.0)then
z3(i,j)=dxy
else
z3(i,j)=-1.0*dxy
endif
else
z3(i,j)=0.0
endif
goto 600
else
!基线比剖面线短
endif
700continue
600continue
500 continue
5 例子
有一航磁数据,经MAPGIS矢量化后如图2原始剖面平面图,经过剖面平面图数字化处理后,用GeoIPAS系统的剖面平面图成图,结果如图3数字化结果成剖面平面图,将原始的基线和剖面线与结果的剖面平面图相互叠加,可以看到两线有部分未完全重合,但相对于整个剖面线值来说误差已经很小,分析原因是:计算基线斜率的精度由有效位数引起,在剖面线与基线的距离变大时其累积的误差也相应变大。

图2 原始剖面平面图
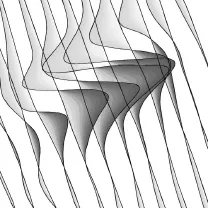
图3 数字化结果成剖面平面图
6 结束语
做剖面平面图数字化时应注意以下几点:
⑴剖面平面图矢量时,基线和剖面线方向要一致,顺序要对应。如有线号,可输入其线号作为属性对应基线和剖面线。
⑵数字化的精度主要取决于矢量图精度,所以在做矢量化时要提高底图的分辨率。
⑶对多幅图拼接的剖面平面图,如果在接图部分比较复杂,要注意基线和剖面线拼接对应关系。
⑷对剖面平面图原图矢量后要在MAPGIS中要做误差校正,应利用所有的图框校正点。
⑸对线文件编辑完成后,需要进行压缩保存文件,然后再做明码文件转换。
⑹剖面平面图数字化结果可成图与原剖面平面图对比检查,保证各基线与剖面线的对应正确,并可检查矢量化精度。
剖面平面图数字化是一个简单方便将剖平图转换为数据的工具,尤其是用在对航磁剖平图老资料的数字化建库中,对提高对老资料的再利用上有很大方便性。
[1]张宏,温永宁,刘爱利.地理信息系统算法基础.北京:科学出版社,2006.
[2]刘天佑.地球物理勘探概论.北京:地质出版社,2007.
[3]张胜业,潘玉玲.应用地球物理学原理.武汉:中国地质大学出版社,2004.
[4]吴信才.MapGIS地理信息系统[M].北京:电子工业出版社,2004.
[5]吴立新,史文中.地理信息系统原理与算法.北京:科学出版社,2003.
[6]林晓彤.Fortran 90编程基础.青岛:中国海洋大学出版社,2006.
[7]彭国伦.Fortran 95程序设计.北京:中国电力出版社,2002.
[8](美)Papheal Pender,苏剑,等.标准C++编程电子工业出版社,2002.
收稿:2014-12-29
DOI∶10.16206∕j.cnki.65-1136∕tg.2015.01.015

