基于场势模型的网络节点重要性综合度量方法

曾 光，陈性元，杜学绘，夏春涛

（1.信息工程大学 密码工程学院，河南 郑州450001；2.信息工程大学 数学工程与先进计算国家重点实验室，河南 郑州450001）

0 引 言

现实世界中，网络被广泛应用于不同领域的复杂数据建模和分析，其中，如何识别和度量网络中的重要节点，具有重要的作用和意义。例如在网络安全的相关研究中，重要节点对于网络攻防两方都具有重要的意义，是双方关注的焦点。特别是对于网络安全工作者而言，如何识别通信网络中的关键路由、发掘自治系统内部网络中的重要设备与系统，是增强网络可靠性与安全性的重要途径之一，吸引了国内外学者的广泛关注，并相应提出了许多结合不同实际背景的方法与模型［1］。本文首先介绍了近年来网络节点重要性度量的研究进展与成果，在此基础上，针对网络节点的重要性受到多种因素影响的问题，提出基于场势模型的网络节点重要性综合度量方法。该方法采用数据场理论对网络节点之间的相互作用关系进行形式化描述，综合考虑影响节点重要性度量的多种因素，使得度量结果客观、准确，与实际应用相符合。

1 相关研究与现状

现有的网络节点重要性度量方法本质上都是源于图论，从静态的网络拓扑结构入手，基于节点之间的位置差异性，从系统科学和社会网络两种角度分析节点重要性的度量问题［1］。

系统科学分析法主要基于节点移除对网络性能的破坏程度来衡量节点的重要性，包括网络连通性、凝聚度、网络效率、生成树数目等性能指标。然而，节点的移除会导致网络的拓扑结构变化甚至被分割，并且节点移除后残留网络之间的节点重要性无法横向比较、节点团收缩后无法判断对称节点重要性等等问题［1，2］。社会网络分析法的核心思想是 “重要性等价于显著性”，在不破坏网络整体性的同时，从节点在网络中的位置特性出发，量化节点的结构重要性，主要包括度、接近度、介数、特征向量、子图、k－核分解［2，3］等常用中心性指标。

上述方法均是针对具体应用问题，分别从不同方面刻画了节点在特定网络的重要性。但是现实网络是复杂多变的，基于单一指标进行网络节点的重要性度量不可避免的会存在片面性问题，如度强调节点与邻居节点的连接数，忽略了邻近节点之间的差异性；介数强调节点对全局网络中信息流的控制能力，忽略了局部网络中节点的差异性。因此，现有的研究思路主要利用节点的多个指标进行综合度量，从不同角度多方位地反映节点的重要程度。如Chen等［4］考虑节点最近邻居和次近邻居的度信息，定义多级邻居指标进行节点重要性度量；任卓明等［5］对文献 ［4］进行改进完善，提出一种综合考虑节点的邻居数与邻居之间连接紧密程度的重要性度量方法；Comin等［6］考虑介数与度的关系进行综合度量；赵毅寰等［7］利用相邻节点间的重要性依赖关系，定义节点重要性贡献矩阵进行介数与度的综合度量；周璇等［8］针对文献 ［7］平均分配节点重要性贡献的不足，引入节点效率参数进行方法的修正与完善；淦文燕等［9－11］利用数据场理论描述所有网络节点间的重要性依赖关系，在将所有节点都视为一致的前提下，定义节点拓扑势来量化节点的位置差异性与重要性。

然而，现实世界的网络中，节点往往并不是数学意义上的一个点，而是由诸多属性特征进行刻画的实体。在网络的实证研究中，重要性的衡量标准与网络实际应用需求密切相关［12］，单纯的依据拓扑结构进行节点重要性度量，忽略了节点的类型、功能等差异性因素。例如网络中的边缘节点，其度都为1、介数都为0，节点的剥离并不影响网络的连通性［2，3］，导致无法有效的区分节点的重要性。同时，由于网络安全策略的复杂性，已有的面向静态拓扑的节点重要性度量方法并不能真实反映各个节点在网络中的重要性。例如在自治系统内部网络中，重要系统在域间控制规则下进行安全交互，可能导致拓扑上连通的两个节点实际并不可达［13］。

本文从计算机网络的应用需求和拓扑特点出发，在上述研究工作的基础上，综合考虑节点的资产价值与互联节点之间的重要性依赖关系来量化节点的重要性，突出边缘节点的区分性，并通过节点可达性矩阵计算节点之间的真实依赖关系，提高节点重要性度量的准确性、客观性与有效性。

2 基于场势模型的网络节点重要性综合度量方法

在计算机网络中，节点的类型、功能和网络的拓扑结构以及安全策略的限制等都是影响节点重要性度量的重要因素之一。本文借鉴数据场理论中场的概念分析网络节点的重要性，引入功能影响因素与安全影响因素，进行网络节点重要性的综合度量。下面给出相关的定义与形式化描述。

2.1 相关概念与描述

定义1 计算机网络的图描述。计算机网络可以用顶点带标签的无向连通图G＝ ｛V，E，LV｝表示，有n 个节点，m 条边。其中，V＝ ｛vi｜1＜i＜n｝代表节点集合，E ＝｛（vi，vj）｜vi，vj∈V，i≠j｝代表边的集合，节点标签lk（vi）表示网络节点vi的标识、类型、功能以及包含的安全策略等特征属性，最终构成节点的标签向量lG（vi）＝｛l1（vi），l2（vi），…，lm（vi）｝。

定义2 邻接矩阵An×n。矩阵元素A［i，j］∈｛0，1｝表示节点vi与节点vj之间是否有边相连，如果A［i，j］＝1，则表示节点之间有边，否则表示节点之间没有边。

定义3 路径矩阵Pn×n。矩阵元素P［i，j］表示节点vi与节点vj之间的路径集合。其中，Pk［i，j］表示路径集合中第k条路径经过的节点序列，｜Pk［i，j］｜表示该路径的长度大小。

定义4 距离d（i，j）。两节点vi和vj的距离表示该节点对之间的最短路径长度。

定义5 网络可达性。表示网络中任意两节点在拓扑连通的前提下，受访问控制等网络安全策略的影响，能够完成信息交互、资源共享的能力。

定义6 accept（lacl）。定义accept（lacl）为给定网络安全策略lacl下，允许连通的节点集合。

定义7 可达性矩阵Racln×n。矩阵元素Racl［i，j］表示节点vi与vj之间在安全策略的限制下，能够进行信息交互的最短路径。

定义8 资产价值value（vi）。定义资产价值表示节点vi的功能重要程度。

定义9 敏感性C（vi）。表示节点vi的系统和信息的公开程度，以及相应信息泄露对整个系统运行造成的危害大小。

定义10 完整性I（vi）。表示保证节点vi的系统和信息不被非授权更改或破坏的能力，以及相应信息被破坏后对整个系统运行的影响大小。

定义11 可用性A（vi）。表示节点vi的系统和信息被授权者按要求访问和使用的能力，以及相应功能间断造成的影响大小。

2.2 节点重要性的综合度量模型

2.2.1 场势模型的引入

在数据场中，网络被描述为一个包含n 个节点的物理系统，其中，每个节点周围都存在着一个作用场，并且场中的任一节点都会受到其余节点的联合作用，同时，节点所受的作用力会随着网络距离的增长而快速衰减。根据数据场的相关理论，目前主要采用代表短程场并且具有良好数学性质的高斯势函数来描述节点之间的相互作用关系，称为拓扑势场［9－11］，如下所示

式中：φ（vi）——节点vi的拓扑势，用于衡量节点的位置差异性；mj——节点vj的质量，用以描述节点的固有属性；d（i，j）——节点vi与vj之间的距离；σ——影响因子，表示节点拓扑势场的作用范围，具体取值参考数据场中的方法［9，10］，采用势熵衡量σ值的合理性，通过求取最小势熵进行确定。相应的势熵定义为

2.2.2 基于资产价值评估的节点质量构造

在现实世界中，网络节点不仅仅是数学意义上的一个点，而是由诸多属性特征刻画的真实个体。例如，在计算机网络中，根据肩负的任务与功能不同，有居于网络中心的核心交换机，也有居于网络边缘的重要服务器，以及对网络的构成影响较小的终端主机。因此，需要引入相应的功能影响因素，突出边缘节点的区分性。

本文参考相关评估标准［14，15］，利用资产价值评估的方法量化网络节点的功能影响因素，作为节点质量引入场势方程中。通过分析资产的类型、关键程度以及内容是否公开等安全需求，采用定性分析的方法将敏感性、完整性、可用性划分为5个等级，分别赋值。其中，C（vi）∈［0，5］，I（vi）∈［0，5］，A（vi）∈［0，5］。资产价值value（vi）由C（vi）、I（vi）和A（vi）采用相乘法原理进行综合计算，公式如下所示

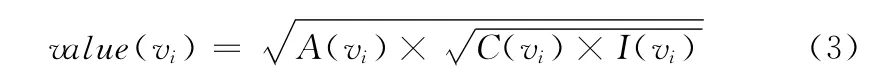
其中，value（vi）∈［0，5］，value （vi）越大，节点vi的资产价值越大，相应的功能重要性也越大。

资产价值等级及描述见表1。

2.2.3 基于安全策略修正的节点可达性矩阵

在计算机网络中，为了满足安全性或隐私保护等需求，人们部署了各种网络安全策略来限制网络的可达性，导致拓扑上连通的两个节点实际并不可达。因此，需要引入相应的安全策略影响因素，计算网络的真实可达性，修正场势模型中节点的影响范围和相应的可作用对象。

表1 资产价值等级及描述

通过分析，计算机网络的可达性计算主要受到网络拓扑结构和路径上各个节点的安全策略等因素影响。根据网络可达性定义，本文依托路径矩阵与安全策略，计算相应的节点可达性矩阵。计算公式如下所示

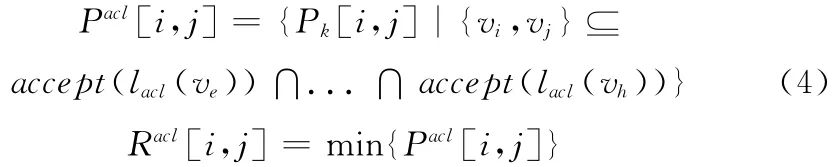
式中：Pk［i，j］——节点vi与vj之间路径集合P［i，j］的第k条路径；lacl（ve），...，lacl（vh）——该路径上节点包含的网络安全策略；accept（lacl（vm））——在网络安全策略lacl（vm）下允许连通的节点集。因此，根据上式计算可以得出在网络安全策略限制下的可达路径集合Pacl［i，j］，以及相应的最短可达路径Racl［i，j］。

2.2.4 基于功能与结构的综合度量模型

本文利用数据场理论的场势模型，结合计算机网络的环境与特点，综合考虑网络节点的功能影响因素、结构影响因素以及安全影响因素，进行节点重要性的综合度量。计算公式如下所示

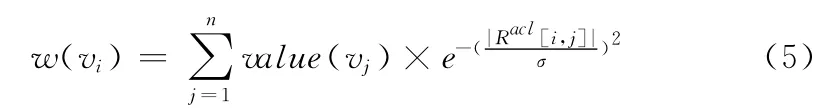
式 中：w （vi）——节 点vi的 综 合 重 要 度；value（vi）——节点的资产价值，代表节点的功能重要性；｜Racl［i，j］｜——节点vi与vj在网络安全策略限制下能够进行信息交互的最短可达路径距离；σ——影响因子，用于调整节点势场的衰减速度和可作用范围。

由式 （5）易知，一个节点的综合重要度的实质为其作用范围内其它节点对该节点作用力的叠加，受到节点本身功能重要性以及邻近可达节点数量和距离等因素的影响。同时，根据高斯函数的数学性质，节点势场的作用范围近似为3σ／，当两节点之间的最短可达路径Racl［i，j］大于此作用范围时，节点间的作用势场迅速衰减为0。因此，可以得出如下3 个基本结论：①节点本身的资产价值越大，该节点的重要性越大，反之亦然；②网络中某节点的邻近可达节点越重要，则该节点的重要性越大，反之亦然；③网络中某节点的邻近可达节点数越多，距离越近，则该节点的重要性越大，反之亦然。

通过分析可以看出，上述公式即能体现节点自身属性的功能影响因素，又能定量反映节点拓扑位置差异的结构影响因素，同时兼顾了安全策略对网络真实可达性的影响，使得度量结果更为精确合理，与事实相符。

2.3 节点重要性度量算法

2.3.1 算法的设计与描述

根据上述综合度量模型，本文算法主要包括4个基本步骤：

（1）节点资产价值的计算。根据资产价值评估方法量化网络节点的安全需求，进行节点功能属性的相应赋值，并代入式 （3）计算节点的资产价值。

（2）节点可达性矩阵的计算。根据节点的邻接矩阵，通过Floyd－Warshall算法获取节点的路径矩阵，同时对网络安全策略进行相应的预处理，计算accept（lacl（vi）），最后通过式 （4）计算节点的可达性矩阵。

（3）影响因子σ的优选。根据高斯函数的数学性质［9］，分别令σ取离散值／3，2／3，...，计算节点的场势和势熵。对应于上述的σ取值，势熵呈现出 “先递减，后递增”的规律，存在相应的极小值，因此进一步以（l－1）／3，（l＋1）／3）为优化区间搜索满足精度要求的最小势熵，以及其对应的优化σ值。

（4）根据上述模型参数，代入式 （5）计算每个节点的综合重要度，并按重要度的大小进行顺序输出。

综上所述，算法的具体描述如下所示：

／＊Input：网络G＝（V，E，LV），其中V ＝｛v1，v2...，vn｝，｜E｜＝ m，LV ＝ ｛lG（v1），...，lG（vn）｝， ｛lC（vi），lI（vi），lA（vi），lacl（vi）｝lG（vi）＊／／＊Output：按从大到小的顺序输出每个节点及其重要度w（vi）＊／Procedure Node＿Importance＿Cal（G）Initialization：1.Initialization the adjacency matrix An×nof graph G ；2.Calculate the Pn×nbased on the An×n； ／／Floyd－Warshall算法3.Initialization the Racln×n with 0；4.for every node vi ∈Vdo 5. Initialization accept（lacl（vi））based on the lacl（vi）；6. Initialization value （vi）＝1／n； ／／兼容式 （1）Node Importance Calculate：7.for every node vi ∈Vdo ／／计算节点资产价值8. Calculate value （vi）based on｛lC（vi），lI（vi），lA （vi）｝；／／式 （3）9.for every node vi ∈Vdo ／／计算节点可达性矩阵10. for every node vj ∈V（i≠j）do 11. for every Pk ［i，j］do ／／依路径大小顺序增长12. if ｛vi，vj｝ accept（lacl（ve）） ∩... ∩accept（lacl（vh））then 13. Racl［i，j］＝Pk［i，j］； ／／式 （4）14. Racl［i，j］＝∞； ／／在影响范围内不存在可达的情况15.for every node vi ∈Vdo ／／影响因子σ的优选16. Calculate l＿reach＿neigh （vi，l）based on Racl［i，x］；17. Initialization w（vi）＝value（vi）；18.Initialization l＝0；19.Initialization H ＝min H ＝－∑n value（vi）Z ；20.while H ≤min Hdo 21. l＝l＋1；σ＝槡i＝1 Z log value（vi）（ ）2l／3；22. for every node vi ∈Vdo ／／式 （5）计算节点综合重要度23. Calculate w（vi）based on value（vi），l＿reach＿neigh（vi，l），σ 24. Calculate H based on w（vi）； ／／式 （2）2（l＋1）／3）26.W ＝Sorted list of（vi，w（vi））in non－increasing order according to their w （vi）values；27.return（W）；25. search for the minHin the range（槡2（l－1）／3，槡

2.3.2 算法的复杂性分析

根据上述的算法和步骤，首先，需要计算所有节点之间的路径矩阵，一般采用Floyd－Warshall算法进行计算，算法的计算复杂度为O（n3）。其次，网络安全策略的处理与转换需要O（ngd）的时间［13］，其中，g 表示网络中一个ACL的最大规则数，每条规则有d 个过滤域段，本算法中取d 为2，即 ｛源IP 地址，目的IP 地址｝。随后，根据网络安全策略计算节点可达性矩阵需要进行kn2次交集操作，算法的计算复杂度为O（kn2），其中k 为获得最短可达路径前计算的最大路径数。最后，基于影响因子σ 的优选进行节点重要性度量，最坏情况下的计算复杂度为O（n2）［9］。考虑到预处理的并行性，可以得出算法最坏情况下的计算复杂度为O（n3＋kn2＋n2），即O（n3）。

3 实例验证与分析

本文以典型的计算机网络为研究对象［15，16］，并依据图模型进行相应的抽象转化，如图1所示。其中，G1代表对外公开的服务器区，G2代表内部办公的服务器区，G3代表内部办公区，G4代表外部访问区。相应的系统资产价值评估［15］与网络安全策略部署情况［16］分别见表2、表3。

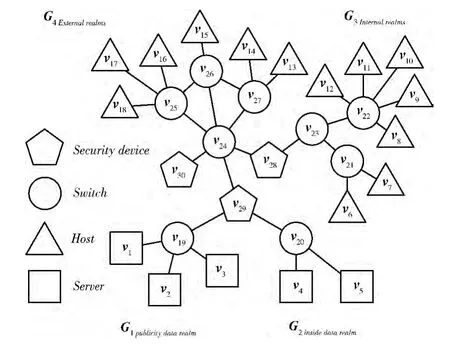
图1 政务办公网络

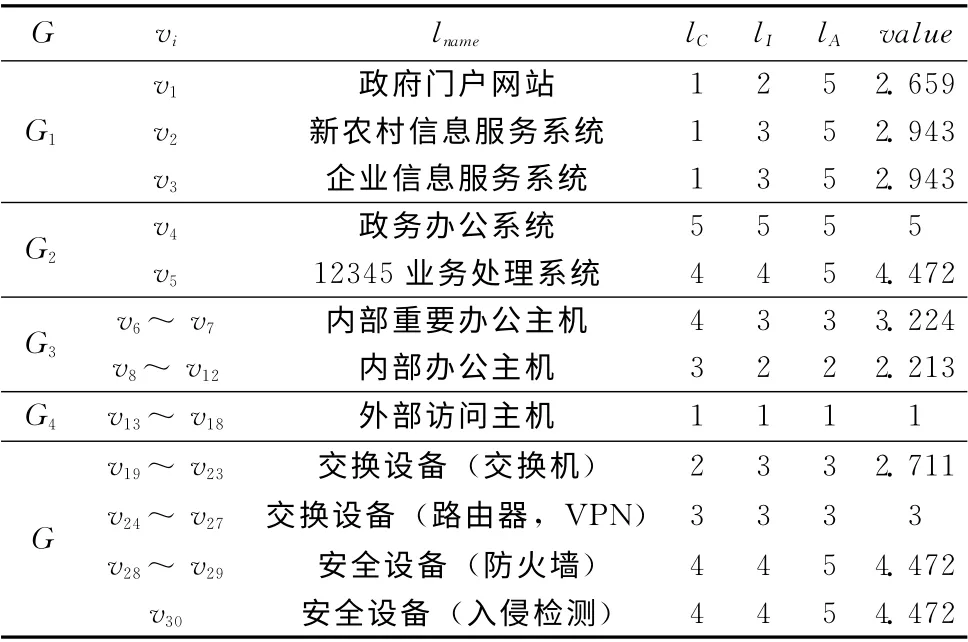
表2 不同网络设备的功能重要性评估

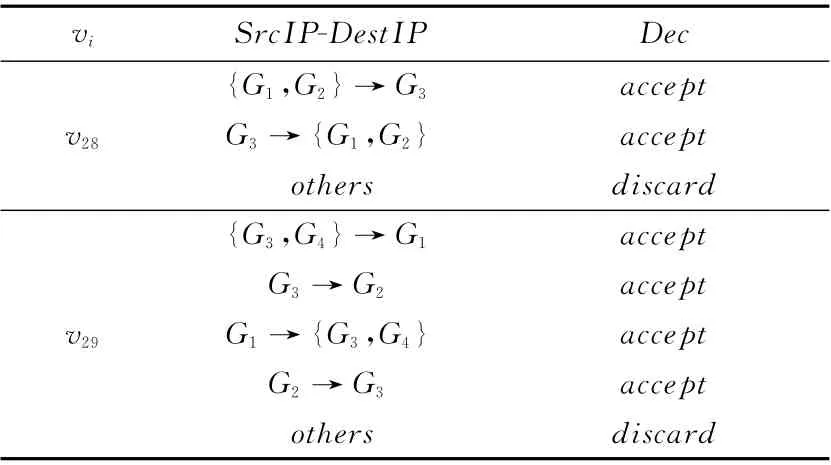
表3 网络安全策略部署情况

根据表3所示的网络安全策略约束，通过式 （4）对路径矩阵进行相应修正，计算节点的可达性矩阵，反映节点在网络拓扑中的真实连通性。随后利用高斯函数的性质对σ值的优化区间进行估计，并求解σ 的优化值。最后，将所得参数代入式 （5），即可获得所有节点的综合重要度，结果如表4所示，并与文献 ［5］、文献 ［8］和文献 ［10］所述方法的度量结果进行对比。为了便于对比分析，分别将各方法的节点重要性度量结果进行归一化处理。

表4 政务办公网络的节点重要性度量结果

如表4所示，上述方法所得的节点重要性度量结果有所差异，原因是各方法判断的侧重点不同。文献 ［5］强调节点局部位置特征的差异性，关注节点的邻居数与邻居之间的连接紧密程度，因此 ｛v24，v25，v27，v26，v29｝等度数较高的节点排序靠前；文献 ［8］综合考虑节点在信息流通中所起的作用和邻居节点的重要度贡献，因此 ｛v24，v26，v25，v29，v27｝等网络效率较高的节点排序靠前；文献 ［10］用拓扑势量化节点的位置差异性，将节点重要度贡献扩展到全局，因此 ｛v24，v22，v25，v26，v29｝等邻近节点较密集的节点排序靠前。通过分析易知，文献 ［5，8，10］的度量方法主要关注节点在网络中的连通性，因此v19～v29等起连通作用的网络节点都具有较高的重要度。而对于边缘节点v1～v18，由于其度值为1，并且通常以星型网络的形式部署，导致无法有效的区分节点之间的重要性差异，如v4与v6；同时，由于主机数量较多，通常处于网络连接紧密区的边缘，具有较高的重要度，因此往往得出主机比服务器更重要的错误结论，如w （v8）＞w （v1）＞w （v4）。资产价值评估方法主要考虑节点的类型、功能等属性差异因素，如 ｛v4，v5，v28，v29，v30｝等事关网络核心业务与安全的节点都具有较高的重要度，但却无法识别v19～v27等交换设备在网络中的连通性差异。

根据度量结果所示，本文方法综合考虑节点本身的功能价值和节点在网络中的连通性作用，给出了较合理的评价结果。如v24作为最重要节点，起着连通整个网络的枢纽作用，与文献 ［5，8，10］的结果相一致； ｛v29，v20｝作为次重要节点，分别肩负着连接对外公开服务器区和内部办公服务器区的重要责任，反映了节点的邻近节点越重要，节点越重要这一重要事实； ｛v23，v19，v26，v25，v28，v27｝作为支撑网络交互通信的节点，同样具有较高的重要度，反映了节点的邻近节点越多、距离越近，节点的重要性越大这一基本特征；而对于边缘节点v1～v18，方法充分考虑节点功能因素，得出w（v4）＞w（v5）＞w（v6）＞w（v2）＞w（v1）＞w（v8）＞w（v13），反映了节点本身资产价值越大，重要性越大的现实规律。同时，由于网络中安全策略的限制与影响，如G4→／ ｛G2，G3｝，需要修正节点v25～v27与其它节点的真实可达性，相应节点在整个网络中所起的连通性作用有所下降，因此与文献 ［5，8，10］的结果相比，节点重要性排序有所下降。通过对比分析表明，本文方法能够准确、有效的度量网络节点的重要性，度量结果与事实更相符。

4 结束语

在网络安全的相关研究中，准确的度量节点的重要程度，是增强网络安全性的重要基础和途径之一。本文利用数据场理论的场势模型，综合考虑网络节点的功能影响因素、结构影响因素以及安全影响因素，提出一种基于场势模型的网络节点重要性综合度量方法。该方法利用数据场描述网络节点之间的相互作用关系，根据节点的资产价值和互联节点之间的作用关系来量化节点的重要性，突出边缘节点的区分性。同时，引入安全影响因素，通过定义节点可达性矩阵修正节点势场的可作用范围，进一步提高节点重要性度量的准确性和客观性。实验分析结果表明，该方法能够更准确地度量节点的重要性，有效区分节点之间的差异性，特别是边缘节点之间的重要程度差异。

［1］LIU Jianguo，REN Zhuoming，GUO Qiang，et al.Node importance ranking of complex networks ［J］.Acta Phs Sin，2013，62 （17）：178901 （in Chinese）.［刘建国，任卓明，郭强，等.复杂网络中节点重要性排序的研究进展 ［J］.物理学报，2013，62 （17）：178901.］

［2］Kitsak M，Gallos LK，Havlin S，et al.Identification of influential spreaders in complex networks［J］.Nature Physics，2010，6 （11）：888－893.

［3］Zeng A，Zhang CJ.Ranking spreaders by decomposing complex networks ［J］.Physics Letters A，2012，377 （14）：1031－1035.

［4］Chen D，LüL，Shang MS，et al.Identifying influential nodes in complex networks ［J］.Physica A：Statistical Mechanics and its Applications，2012，391 （4）：1777－1787.

［5］REN Zhuoming，SHAO Feng，LIU Jianguo，et al.Node importance measurement based on the degree and clustering coefficient information ［J］.Acta Phs Sin，2013，62 （12）：128901（in Chinese）.［任卓明，邵凤，刘建国，等.基于度与集聚系数的网络节点重要性度量方法研究 ［J］.物理学报，2013，62（12）：128901.］

［6］Comin CH，Da Fontoura Costa L.Identifying the starting point of a spreading process in complex networks［J］.Physical Review E，2011，84 （5）：056105.

［7］ZHAO Yihuan，WANG Zulin，ZHENG Jing，et al.Finding most vital node by node importance contribution matrix in communication networks ［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35 （9）：1076－1079 （in Chinese）.［赵毅寰，王祖林，郑晶，等.利用重要性贡献矩阵确定通信网中最重要节点 ［J］.北京航空航天大学学报，2009，35 （9）：1076－1079.］

［8］ZHOU Xuan，ZHANG Fengming，LI Kewu，et al.Finding vital node by node importance evaluation matrix in complex networks［J］.Acta Phs Sin，2012，61 （5）：190201 （in Chinese）. ［周漩，张凤鸣，李克武，等.利用重要度评价矩阵确定复杂网络关键节点［J］.物理学报，2012，61 （5）：050201.］

［9］GAN Wenyan，HE Nan，LI Deyi，et al.Community discovery method in networks based on topological potential［J］.Institute of Software，2009，20 （8）：2241－2254 （in Chinese）.［淦文燕，赫南，李德毅，等.一种基于拓扑势的网络社区发现方法 ［J］.软件学报，2009，20 （8）：2241－2254.］

［10］JIANG Jian，GAN Wenyan，ZHAO Dongjie，et al.Analysis of local centrality in social communication network based on topology potential［J］.Journal of Systems Engineering，2010，25 （6）：861－866 （in Chinese）. ［江健，淦文 燕，赵东 杰，等.基于拓扑势的社会通信网局域中心性分析 ［J］.系统工程学报，2010，25 （6）：861－866.］

［11］Zhang J，Xu XK，Li P，et al.Node importance for dynamical process on networks：A multiscale characterization ［J］.Chaos：An Interdisciplinary Journal of Nonlinear Science，2011，21 （1）：016107.

［12］Huang X，Vodenska I，Wang F，et al.Identifying influential directors in the united States corporate governance network［J］.Physical Review E，2011，84 （4）：046101.

［13］PU Tianyin，RAO Zhengchan，QIN Zheng.Research on accessibility and analyze its key technologies under the environment of computer network ［J］.Journal of Hunan University of Science ＆ Technology （Natural Science Edition），2013，28 （2）：86－89 （in Chinese）.［蒲天银，饶正婵，秦拯.计算机网络环境下可达性研究关键技术分析 ［J］.湖南科技大学学报 （自然科学版），2013，28 （2）：86－89.］

［14］GB／T 20984－2007：Risk assessment specification for information security ［S］.2007 （in Chinese）. ［GB／T 20984－2007：信息安全风险评估规范 ［S］.2007.］

［15］ZHANG Yang.Research on network information system asset assessment［D］.Beijing：Beijing University of Posts and Telecommunications，2013 （in Chinese）. ［张洋.网络信息系统资产评估研究 ［D］.北京：北京邮电大学，2013.］

［16］GB／Z 24294－2009：Guide of implementation for internet－based e－government information security ［S］.2009 （in Chinese）.［GB／Z 24294－2009：基于互联网电子政务信息安全实施指南［S］.2009.］