基于CMOR 的跳频信号参数盲估计算法

万乔乔，张俊然，龚晓峰

（四川大学 电气信息学院，四川 成都610065）

0 引 言

如何有效地提取跳频信号的各性能参数并对其进行实时监测，以提高频谱资源利用率，是当前无线电频率检测管理首要解决的问题［1，2］。传统的利用短时傅里叶变换（STFT）提取性能参数的主要做法是，人为地选择一合适大小的矩形窗，并对信号做STFT 变换以从时频分布图上提取跳频频率和跳速等，虽然可以提取，但是固定矩形窗的大小严重影响着参数的估计精度［3］；而一般意义上的先利用小波变换［4］，再在频谱图上求跳速的方法虽然理论上可行，但是由于具体复杂的电磁环境及实际环境中的噪声干扰等问题，其可行性较差。

本文基于CMOR，通过充分挖掘Morlet小波系数的尺度与跳频信号频率之间的一种内在联系，准确地得到了跳频信号的时频分布图［5］，再从时频分布图准确地估计出跳频信号的跳频频率。再利用sym4 （symlets函数系symN （N＝2，3，…，8）的缩写）小波分解较高的滤波特性，准确地估计出跳频信号的边缘跳变点，进而估计出了跳频周期与跳速等参数。目前大多数算法只是建立在分析理想信号的基础上，缺乏实际应用测试，本文不仅用仿真信号对算法进行了说明，还用信号源N5182A （Agilent N5182A3G／6G MXG 射 频 矢 量 信 号 发生器，频率范围是250KHz至3GHz或6GHz，其射频与微波：宽带I／Q 调制）发出的实际的跳频信号进行了测试，较高的实时性和准确性说明所提算法具有较高的实际应用价值。

1 Morlet小波变换原理

连续小波变换 （CWT）的定义见参考文献 ［6－8］，其表达式为

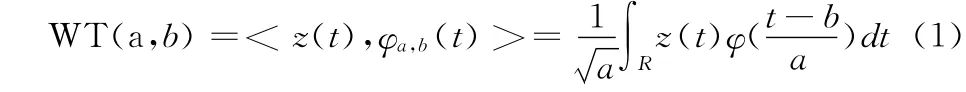
由式 （1）可以看出，小波变换是一种积分变换，称WT（a，b）为小波变换系数。其中更重要的是，小波基具有尺度因子a和平移因子b。

Morlet函数小波是以单频率复正弦方式调制的一种高斯波，它的时、频表达式如下：时域表达式

频域表达式

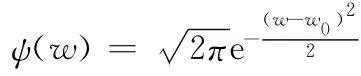
从时域表达式上看，w 只影响φ（t）虚部，显然w 的值不同，φ（t）的包络区域不会变，只是包络区对应的正弦波形的频率会改变；从频域表达式看，当w0＝w0′时，ψ（w）的中心频率会变为w′0，但是带宽保持不变；因此Morlet小波函数实际上是一种复小波变换，其在时、频域都具有良好的局域特性，常常用于时频分析以及复信号的分解中。

Morlet小波变换见参考文献 ［9－11］，其离散化形式为

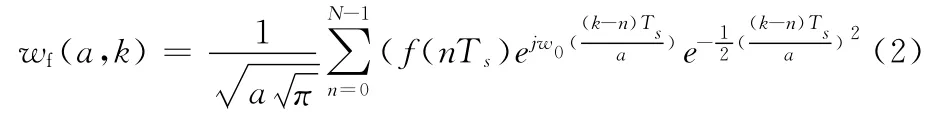
式 （2）中对应于某给定尺度a 的信号子波变换的结果就相当于滤波器的时域输出，输出的瞬时功率是返回系数模值的平方，a取不同的值就代表在不同的频段对信号的功率谱进行估计。总结来说，Morlet小波变换的实质就是其具有带通滤波特性，以此清晰地观察到信号的边缘跳变点等性能参数。应的尺度序列 （矩阵的行），亮度的深浅代表CMOR 变换系数幅值的大小，颜色越亮的地方CMOR 的系数值越大。取CMOR 系数模值在各个时间点的最大值，得到信号的跳变规律如图2所示。

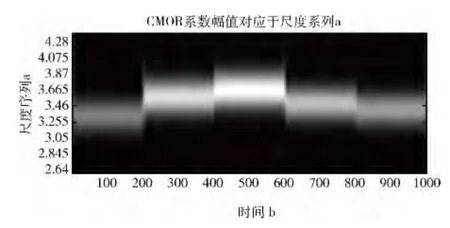
图1 CMOR 时频图

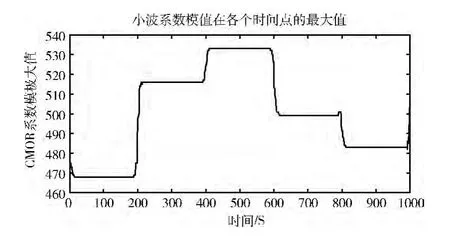
图2 CMOR 系数模极大值

图2可以看出CMOR 系数模值已经很好地反应了跳频信号频率跳变的规律，但是在跳变点存在抖动和尖峰，为了消除在上升沿或下降沿存在的这种抖动和尖峰，本文采用离散小波分解对信号进行滤波，具体做法是：采用sym4小波对CMOR 系数模极大值序列做三层分解，并且取其低频系数进行重构。取平滑处理后小波系数模值的第一跳来说明滤波效果，如图3所示。

2 基于小波的跳频信号参数估计算法

跳频信号参数盲估计，主要包括跳频信号的周期、跳速及其跳频图案。本文先用MATLAB 生成的跳频信号来验证算法，根据常规接收机系统中码速率和采样率的取值关系，在这里选取码速率为100Hz，采样率为20倍的码速率，跳变次数5次，总共1000个采样点数。跳频周期为5 ms，跳频频率集为 ｛f1＝200 Hz，f2＝320 Hz，f3＝360 Hz，f4＝280 Hz，f5＝240 Hz｝［12］。对此信号做CMOR，选择Morlet复小波的中心频率fc＝3；带宽db＝3；尺度scall＝ ［1：0.005：5］。CMOR 之后得到信号的时频分布图如图1所示。

CMOR 的返回系数是一个矩阵，在图1中，横轴代表时间，对应信号的采样点 （矩阵的列），纵轴是CMOR 对

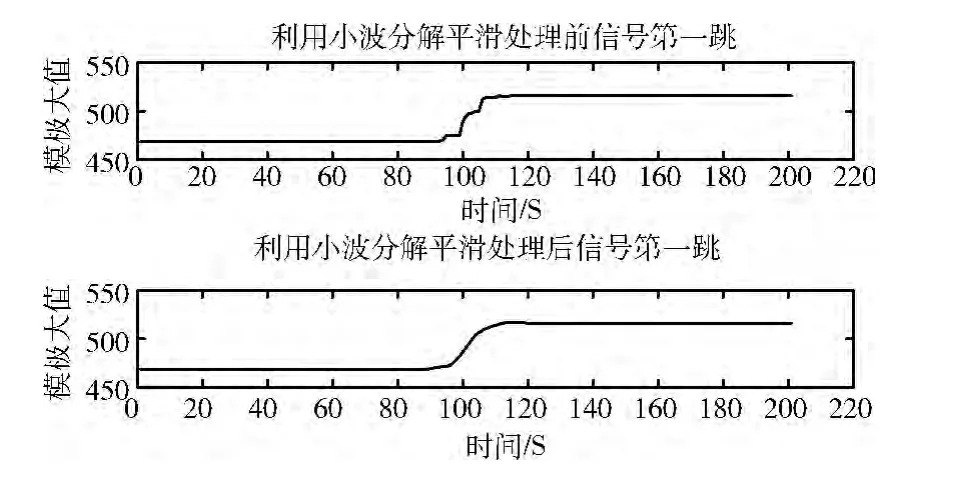
图3 CMOR 系数模极大值对应于信号的第一跳

对滤波处理后的信号再进行求导操作，来捕获信号跳变点的准确位置，如图4所示。

并对求导后的曲线进行 “谱峰搜索”准确捕获跳变时刻以及跳速，统计结果见表1。

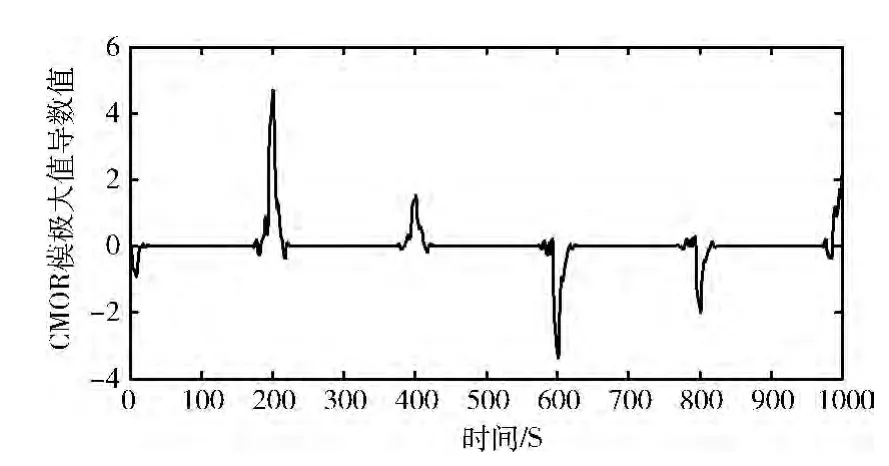
图4 信号的跳变时刻

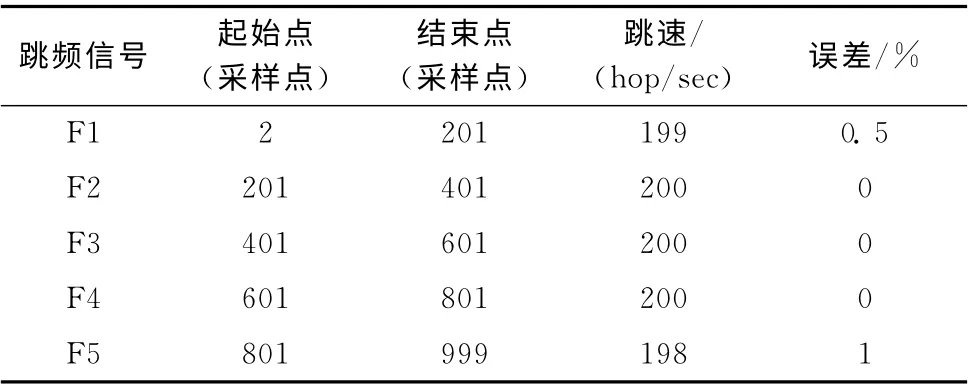
表1 跳变时刻

对表1的跳速求平均值，得到跳速V＝ （199＋200＋200＋200＋198）／5＝199.4 （hop／s），即 每 秒199.4 跳；然后再根据公式T＝1／V，得到跳频信号的跳频周期T＝5.02ms。

在估计出跳变时刻的基础上，再次充分挖掘CMOR 系数的实质含义，研究发现有如下关系式：Fa＝Fc×fs／A，其中Fc为小波的中心频率，fs为信号的采样率，A 为尺度，Fa为对应的跳频频率。得到了Fa就得到了跳频信号的时间－频率曲线，如图5所示。相应的跳频信号的频率值见表2。

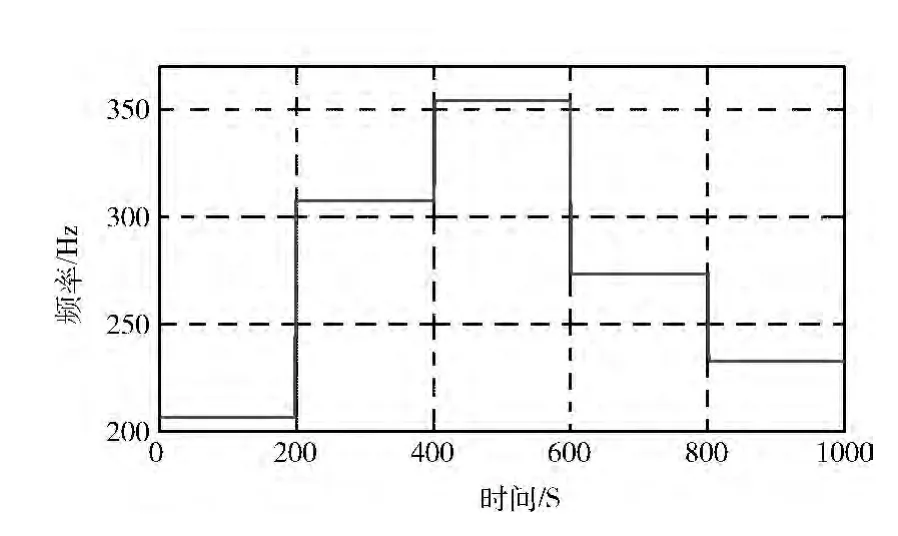
图5 跳频信号的时间－频率曲线

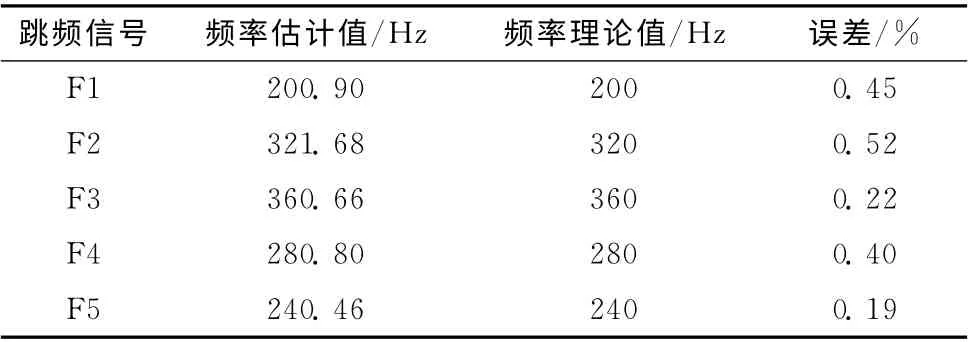
表2 跳频信号频率

以上仿真结果显示，CMOR 算法可以准确捕获到信号的跳变时刻，并求出其跳频频率。基于CMOR 的跳频信号参数估计算法流程如下：①选择合适的尺度，对信号做一维连续小波变换，并求得小波变换系数的模极大值；②对小波变换系数的模极大值做3 层尺度’sym4’小波分解，取其分解后的低频系数进行重构，相当于对信号进行低通滤波，去除高频干扰；③对滤波处理后的模极大值序列进行求导操作，捕获其跳变时刻；据跳变时刻求出跳频信号周期，其倒数即为跳频信号的跳速；④根据Morlet小波变换系数模极大值序列的尺度序列与跳频信号频率之间的内在联系，求得跳频信号的频率值。

3 算法验证

3.1 实验平台搭建

由于仿真信号是在理想环境下，本文用实测信号来验证算法的合理性。实验用的信号源是N5182A，在华日通讯技术有限公司的实验基地，信号源经一个天线发射出去，经空中传播后，再由另一个连接接收机的天线接收，接收机为双通道接收机PXI－1045，信号采用正交的采样方式，其中I是同相分量，Q 是正交分量，实验平台如图6所示。

图6 实验平台

3.2 跳频信号测试

信号源N5182A 发出的跳频信号，其采样带宽为100 kHz，中心频率为88.05 MHz，采样率为125kHz，每帧长度为65536，跳频周期为80ms。为了验证算法的合理性和实用性，在一天的不同时间段在接收机端连续采集跳频信号，并对每次采集的信号进行100多次测试，在这里任选其中几组，观察其在每个跳变点的信息。跳频信号的频谱如图7所示。

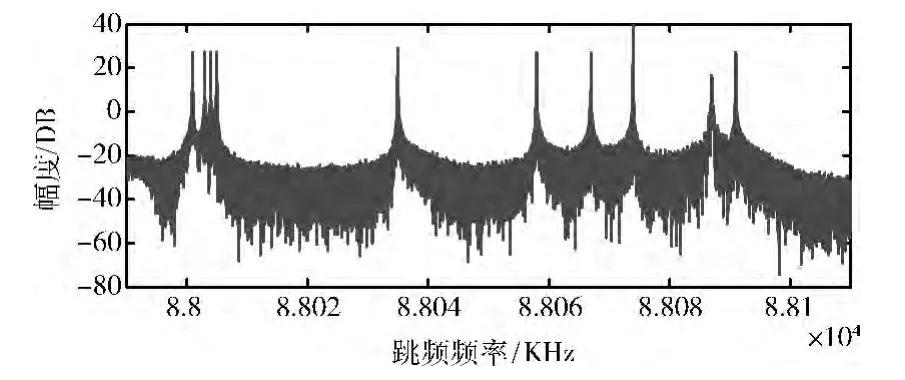
图7 实测跳频信号频谱

对测试信号进行CMOR，且平滑滤波处理前后的信号如图8所示。得到最终的时频曲线如图9所示。

图8 CMOR 模极大值滤波前后

图9 跳频信号的时间－频率曲线

跳频信号的跳速和跳频频率分别见表3和表4。

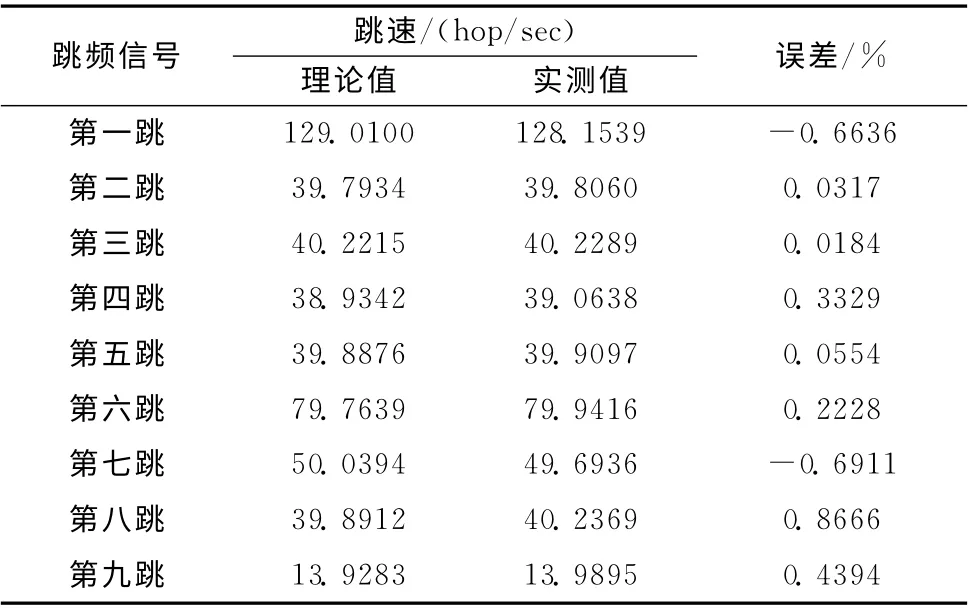
表3 Morlet复小波估计跳速

表4 Morlet复小波估计跳频频率

为了更直观地显示结果，对不同时间段的跳频信号的跳速和跳频频率分别做误差曲线评估，如图10、图11 所示，其中纵坐标分别代表跳速和跳频频率理论值与估计值的相对误差。

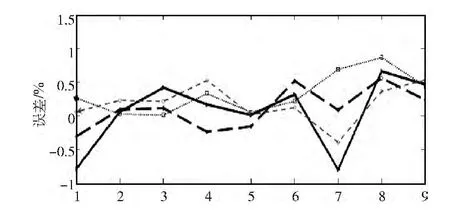
图10 跳速误差评估曲线

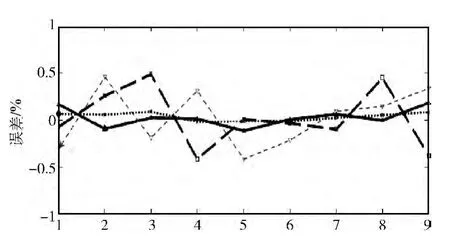
图11 跳频频率误差评估曲线

图10和图11的跳速和跳频频率的误差评估曲线显示，基于Morlet小波的新的跳频信号参数盲估计算法，其估计误差的绝对值均小于1%。为了说明新的算法在估计精度方面的优势，将其与其他算法的结论做对比：文献 ［13］的结论见表5；文献 ［14］的结论见表6，表6中mi代表每一个跳变点，Th代表每一跳的驻留时间，由此计算出跳频周期的估计值与真实值的平均相对误差为±1.82%。

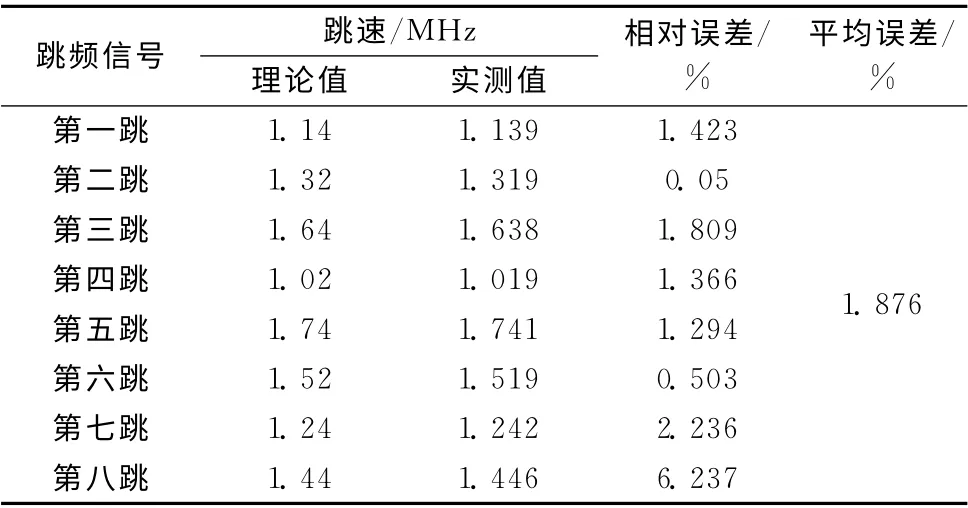
表5 文献 ［13］表4.2的跳频频率估计值

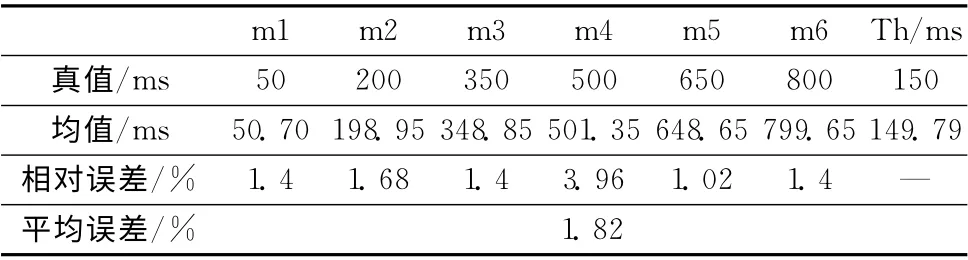
表6 文献 ［14］表1的跳频周期估计值

对比显示，新算法的估计精度更高。

4 结束语

本文通过充分挖掘Morlet小波变换后小波系数所代表的本质含义，即利用小波系数模极大值对应的尺度与测试信号频率之间的密切关系，提出了一种新的基于CMOR 的跳频信号参数盲估计算法，以达到参数估计的目的。仿真和实测信号结果均表明，新的算法准确地估计出了跳频信号的各性能参数，而且估计精度很高。此算法可以适应于目前常用的数字接收机系统中，并在接收机系统中已经得到了初步的应用。但是如果将此方法用于分析目前学术界正在探索的变跳速的跳频信号，还存在一定的局限性。此外还可以考虑对算法进行进一步的改进，如跳频信号的调制识别、通信对抗中信号的侦察与接收、高跳速跳频电台的干扰研究及跳频电台的同步等问题。

［1］CHEN Feng.Real－time spectrum detection system ［J］.Railway Technology Innovation，2011 （6）：47－49 （in Chinese）.［陈峰.实时频谱侦测系统 ［J］.铁路技术创新，2011 （6）：47－49.］

［2］LIU Qi，SU Wei，LI Chengshu，et al.Adaptive spectrum sharing scheme based on FH communications ［J］.Acta Electronica Sinica，2010，38 （1）：105－110 （in Chinese）.［刘琪，苏伟，李承恕.基于跳频的自适应频谱共享方案 ［J］.电子学报，2010，38 （1）：105－110.］

［3］ZHANG Wei.Radio frequency up cost special fund collection，management，policy analysis ［J］.China Radio，2013 （5）：18－20 （in Chinese）.［张伟.无线电频率占用费专项资金收取、管理政策解析 ［J］.中国无线电，2013 （5）：18－20.］

［4］ZHOU Lu，WU Qian，LUO Chaohong，et al.A new kind of frequency hopping signal jump speed blind estimation algorithm［J］.Telecommunications Technology，2008，48 （8）：73－77（in Chinese）.［周露，吴潜，罗朝洪.一种新的跳频信号跳速盲估计算法 ［J］.电讯技术，2008，48 （8）：73－77.］

［5］Deng Fang，Chen Jie，Chen Chen.Adaptive unscented Kalman filter for parameter and state estimation of nonlinear highspeed objects ［J］.Journal of Systems Engineering and Electronics，2013，24 （4）：655－665.

［6］Zhang Lei，Li Yachao，Liu Yan，et al.Time－frequency characteristics based motion estimation and imaging for high speed spinning targets via narrowband waveforms［J］.Science China（Information Sciences），2010，53 （8）：1628－1640.

［7］MAO Zhongyang，ZHAO Peihong，WANG Hongxing，et al.A non－stationary signal analysis based on the phase modulation signal demodulation algorithm ［J］.Journal of Naval Aeronautical Engineering Institute，2012，27 （5）：525－529 （in Chinese）.［毛忠阳，赵培洪，王红星，等.一种基于非平稳信号分析的时相调制信号解调算法 ［J］.海军航空工程学院学报，2012，27 （5）：525－529.］

［8］ZHANG Yaqi，CAI Hua.Based on DFT，DCT and wavelet transform image compression with Matlab ［J］.Computer Knowledge and Technology，2013 （21）：4929－4932 （in Chinese）.［张雅琪，才华.基于DFT、DCT 和小波变换图像压缩 与 Matlab 实 现 ［J］.电 脑 知 识 与 技 术，2013 （21）：4929－4932.］

［9］LIU Jiantao.Frequency hopping signal blind parameter estimation algorithm research and implementation ［D］.Chengdu：University of Electronic Science and Technology，2007 （in Chinese）.［刘健涛.跳频信号参数盲估计算法研究及实现 ［D］.成都：电子科技大学，2007.］

［10］FENG Tao，YUAN Chaowei.Frequency hopping signal，a new method of time－frequency analysis［J］.Journal of Beijing University of Posts and Telecommunications，2010，33 （3）：10－14 （in Chinese）. ［冯涛，袁超伟.跳频信号的时频分析新方法 ［J］.北京邮电大学学报，2010，33 （3）：10－14.］

［11］ZHANG Xi，WANG Xing，DU Xingmin.Based on the wavelet transform parameters of frequency hopping signal blind［J］.Circuit and the Journal of Communication Systems，2009，14 （4）：60－65 （in Chinese）.［张曦，王星，杜兴民.基于小波变换的跳频信号参数盲估计 ［J］.电路与通信系统学报，2009，14 （4）：60－65.］

［12］LI Chan，CUI Xiaowei，LI Guomin，et al.The phase truncation noise influence in the GPS receiver digital delay lock loop tracking performance analysis［J］.Journal of Tsinghua University （Natural Science Edition）Network，2008，48 （4）：522－525 （in Chinese）. ［李蝉，崔晓伟，李国民，等.GPS接收机中相位舍位噪声影响数字延迟锁定环跟踪性能的分析［J］.清华大学学报 （自然科学版）网络，2008，48 （4）：522－525.］

［13］YU Dan.Frequency hopping signal blind parameter estimation algorithm research ［D］.Dalian：Dalian University of Technology，2008 （in Chinese）.［于丹.跳频信号参数盲估计算法研究 ［D］.大连：大连理工大学，2008.］

［14］ZHANG Shichao.Frequency hopping signal blind detection and parameter estimation research ［D］.Chengdu：University of Electronic Science and Technology，2012 （in Chinese）.［张仕超.跳频信号的盲检测与参数盲估计研究 ［D］.成都：电子科技大学，2012.］