基于朴素贝叶斯K近邻的快速图像分类算法

张旭，蒋建国，洪日昌*，杜跃

(1.合肥工业大学 计算机与信息学院，合肥230009;2.陆军军官学院 计算机教研室，合肥230031)

图像分类是计算机视觉研究中的热点内容之一，在图像标注［1］、多媒体信息检索［2］等领域均有广泛的应用.图像分类技术大致分为以下两大类:基于学习过程的图像分类方法和非参数的图像分类方法.目前，基于学习过程的分类方法仍是图像分类与识别领域内的主流，特别是随着视觉词袋模型(BoVW)［3］的提出与应用，然而在实际情况中往往存在训练样本不足以及过拟合等问题.而非参数的分类方法不需要参数学习的过程，能够更合理地应用于图像类别较多的分类任务中并且避免了过拟合等问题，相比于基于学习过程的分类方法，基于非参数的分类算法更为简洁.

尽管非参数的分类器存在上述优点，但其分类性能低于基于学习过程的分类算法［4-7］.文献［8］比较了非参数最近邻(NN)方法与BoVW模型的图像分类性能，实验结果表明后者的分类正确率明显优于前者.而文献［9］提出一种基于朴素贝叶斯最近邻(NBNN)图像分类算法，认为基于非参数的最近邻分类性能在实际应用中被低估，导致其性能下降的原因有两方面:一方面是算法中的特征量化引起量化误差，另一方面是算法采用图像与图像之间的距离进行分类决策.文献［10］在 NBNN算法的基础上提出一种 NBNN Kernel，并与BoVW模型相结合用于图像分类.NBNN算法的成功之处主要在于采用了图像-类别距离(I2C)度量方式，文献［11］在此基础上提出一种线性距离编码的方法，采用图像-类别距离将图像的局部特征转化为更具区分性能的距离向量.文献［12］提出一种Local NBNN的分类算法，文献［13］在此基础上结合BoVW和Local NBNN方法的优点提出一种位置区分性编码方法，通过特征-类别距离而非K-means聚类将局部特征转化为特征向量，从而避免了量化带来的信息损失.Tommasi等［14］基于 NBNN分类器提出一种领域适应学习算法，实验结果进一步证明了NBNN算法思想的有效性.Wang等［15］基于最近邻分类提出一种加权I2C即图像-类别距离学习方法，并采用空间划分和Hubness Score的方法对图像分类进行加速，但这种方法模型复杂，特别是权重学习过程时间复杂度较高.

NBNN算法的主要思想是对测试图像中的每个特征在各类训练图像特征集中寻找其最近邻并计算I2C距离，随着图像类别以及各类图像数目的增加，算法运行速度较慢、内存开销高，影响了其在实际中的应用，并且NBNN算法使用测试图像的一个最近邻特征用于决策分类.在基于稀疏编码的图像分类与物体识别中［16］，硬赋值编码的性能已经被证实低于局部受限软赋值编码，硬赋值编码本质上就是寻找一个最近邻，而局域受限软赋值编码则是寻找邻域内的K近邻，受此启发本文采用特征的K近邻用于分类决策.

一般情况下，一幅图像包含了少量高区分性能的特征和大量低区分性能的特征，部分低区分性能的特征表现为图像常规性的结构信息和背景信息，这部分特征对图像分类贡献较小，但由于其数量较多，搜索最近邻并计算I2C距离需要大量时间.因此，在NBNN算法中选择高区分性能的特征用于分类决策可以有效减小近邻搜索时间及内存开销，为应用于大规模图像分类任务提供了可能.

本文提出一种朴素贝叶斯K近邻(NBKNN)分类算法，在充分利用NBNN算法思想的基础上并非使用特征空间中的最近邻特征而是K近邻特征进行决策分类，并且进一步去除背景信息对分类性能的影响;为了提高算法运行速度、减少算法内存开销，在保证分类正确率的前提下，采用特征选择的方式分别减少测试图像以及训练图像集中的特征数目，并且尝试同时减少测试图像与训练图像集中的特征数目平衡分类正确率与分类时间之间的矛盾.

1 特征量化与图像-类别距离度量

图像分类算法中最常用的两个过程导致了非参数方法分类性能的下降，这两个过程分别是特征量化和图像与图像间的距离测度.

1.1 特征量化

在基于BoVW模型的图像分类算法中，首先在训练样本中提取大量的图像特征，通过聚类构建视觉词典，聚类中心即是视觉词典中的每个单词，然后通过视觉词典将图像表示为直方图空间中具有固定长度的特征向量，这种表示方式对基于SVM等的图像分类方法是必须的.量化产生的视觉词典带来了信息损失，大量具有区分性能的特征被丢弃，但损失的信息在训练学习过程中可以得到一定程度的弥补，从而算法仍可获得不错的分类性能.然而如果将这种图像表示方式用于最近邻图像分类算法中，由于非参数的分类方法中没有训练学习的过程，损失的信息无法得到弥补，因此分类性能较差.

在量化过程中，特征空间中出现频率低的特征往往具有较高的量化误差，而出现频率高的特征量化误差较低.在大部分图像中高频特征往往表现为图像的结构性信息如边缘和拐角，因此该类特征包含有用的信息较少，区分性能较差.而图像中最具区分性能的特征出现频率较低，位于特征空间中的低密度区域，在聚类过程中这部分区域往往无法生成聚类中心，即无法生成视觉单词，因此聚类构建视觉词典的过程中将不可避免地出现量化误差，导致区分性能下降，并且区分性能越高的特征经量化之后其区分性能降低的程度越高.文献［17］采用 p(d|C)/p(d|)描述了特征d区分类别C与其他类别的能力，经过量化后特征d的区分性能描述为p(dquant|C)/p(dquant|)，在Caltech-101图像集中的实验证实了经量化之后图像集中特征的平均区分性能大约下降了60%.

1.2 图像-类别距离度量化

在非参数的图像分类中，量化操作是引起图像分类性能下降的主要原因之一.文献［18］提出一种基于最近邻的图像分类算法，算法使用了Geometric Blur特征并且避免了量化过程，但实验结果仍然差强人意.文献［9］认为造成这种问题的主要原因是采用了图像-图像(I2I)的距离度量方式而非图像-类别(I2C)的距离度量方式.I2I的距离度量方式是实现核方法的基础，然而在基于I2I非参数的图像分类方法中，仅当训练样本足够多并且测试图像(待分类图像)与训练图像非常相似时才能取得很好的分类效果.当训练样本数量较少并且类内图像变化较大时，这种距离度量方式极大地限制了图像分类的泛化性能.在文字识别和纹理图像分类等领域中，基于最近邻的分类器具有较优的分类性能，主要原因是相对于类别的复杂性各类具有数量较多的训练样本.然而在实际情况中，相对于类别复杂度本文所获得的训练样本数目较低，特别是当类别内复杂性较高时，如同类别内的物体具有不同的外观形状和表示形式，基于最近邻的图像分类效果较差.采用I2C的距离测度方式即同时利用类别C中所有图像特征的分布可以获得更好的分类效果和泛化性能［19］.文献［20］证实了在服从朴素贝叶斯假设的条件下，在基于最近邻的图像分类方法中采用I2C的距离度量方式可获得优于I2I的分类性能.

2 朴素贝叶斯最近邻分类

在满足一定的假设条件下，基于朴素贝叶斯最近邻分类器可以获得近似最优贝叶斯分类性能.问题描述如下:对于给定的待分类图像Q(测试图像)，根据训练图像及其类别标签将其划分到相应的类别C中.根据最大后验概率最小化分类误差的原则，测试图像Q按照式(1)被划分为类别中.

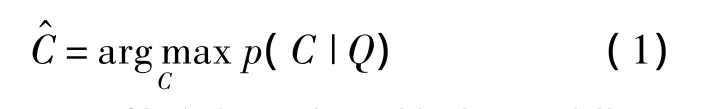
假设类别C服从均匀分布，则根据贝叶斯公式，最大后验概率等价于最大似然概率.式(1)可以改写为

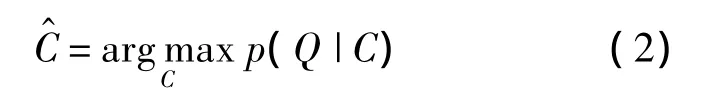
图像Q的特征描述子分别记为 d1，d2，…，dn，假设di符合独立同分布，则

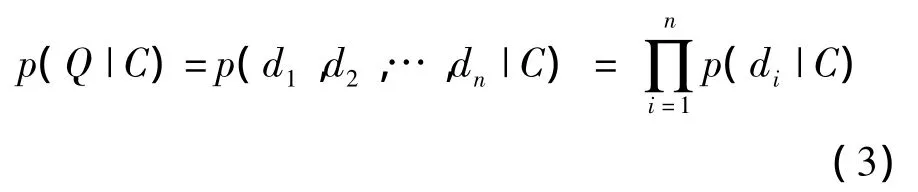
对式(3)取对数运算(底数大于1)，则分类准则如下:

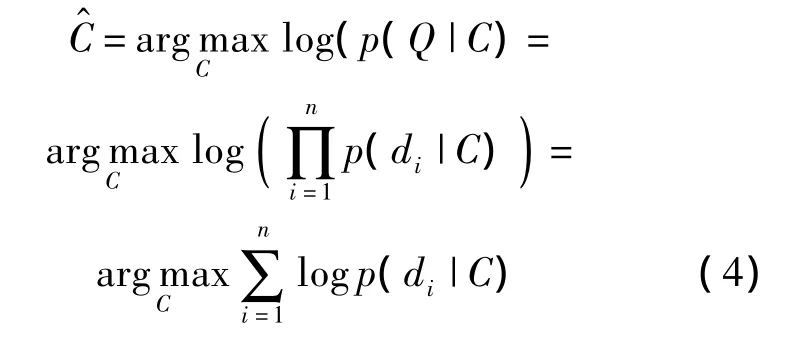
p(di|C)可以通过Parzen窗核函数进行估计:

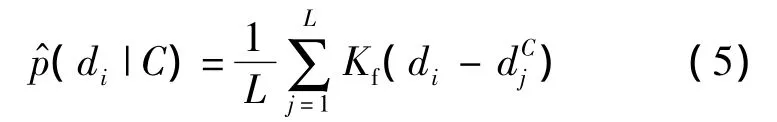
式中，dC1，dC2，…，dCL为类别 C中所有训练图像中的特征描述子，L为特征描述子的个数;Kf为高斯核函数，其值非负并且和为1，如式(6)所示.随着L的逐渐增大，函数的尺度参数σ逐渐减小，p^(di|C)最终趋于p(di|C)的真实分布.

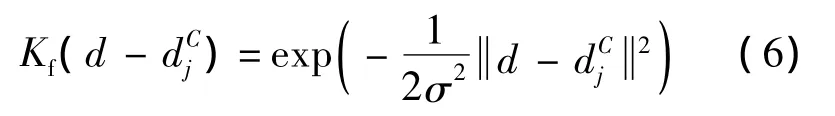
基于最大后验概率的朴素贝叶斯分类器需要计算每个特征d在类别C中的概率分布，虽然可以采用Parzen窗进行估计，但是从每幅图像中提取的局部特征数量巨大，特别是为了获得更高的准确率，需要尽可能多的dCj即类别C中所有图像的局部特征，由于需要计算d和dCj之间的距离，因此算法的时间复杂度较高.考虑特征分布的特性，特征空间中大部分区分性能高的特征相对孤立，类别C内各图像局部特征的分布更是如此.因此随着d与dCj之间距离的增加，式(5)中大部分Kf(di－)项是可以忽略的，仅小部分项(即与d距离足够近的那一部分)起到决定性作用.因此，只需计算Kf(di－dCj)前K项即d在类别C中的K最近邻特征，式(5)改写为

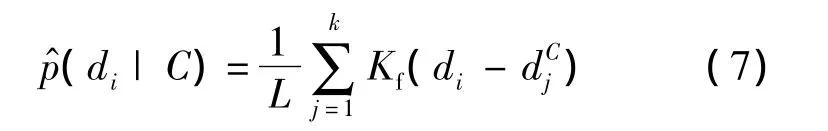
原始NBNN算法中取K为1，即对检索图像中的特征在类别C中寻找其最近邻用于分类决策，实验取得不错的分类性能.

3 朴素贝叶斯K近邻分类

NBNN算法简单有效、分类性能好，并且不需要额外训练学习的过程，避免了参数学习等带来的相关问题.但算法运行速度较慢并仅利用最近邻进行分类识别，这方法类似于BoVW模型中的硬赋值编码方式，尽管取得了不错的分类效果，但没有充分利用其他近邻特征的信息.结合NBNN算法的原理和软赋值编码的思想，本文提出一种朴素贝叶斯K近邻分类算法记为NBKNN算法，分类过程中利用了特征的K近邻信息并去除背景信息对分类性能的影响，算法采用 FLANN［21］搜索近似K近邻，提高了高维特征近邻的搜索速度.

给定测试图像Q以及训练图像库，定义图像Q对于类别C的区分性能RC如下式所示，其中表示不是C的其他类别:

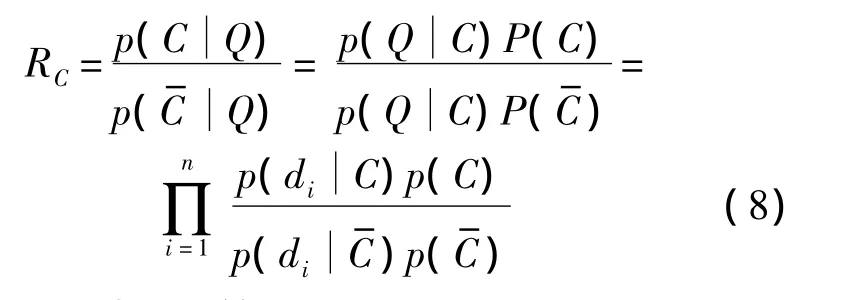
对式(8)取对数运算得

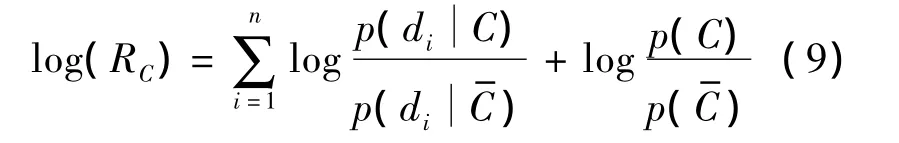
式(9)将图像Q对类别C的区分性能转化为图像中局部特征对类别C的区别性能，因此分类决策可以表示为

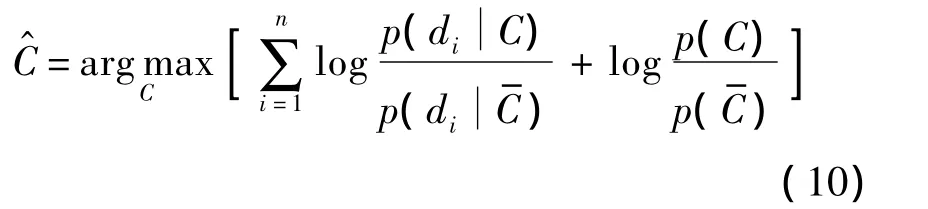
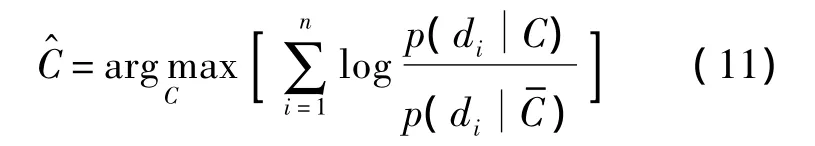
原始 NBNN算法的时间复杂度为O(NQNClog(NTrNT))，其中NTr表示每类别中训练图像的数目，NC表示训练图像集中的类别数目，NQ和NT分别表示测试图像和训练图像中的特征数目，数量众多的特征中很大一部分表征了图像中的背景信息和噪声信息，虽然这些特征对于分类没有起到实质性的作用，但却在很大程度上影响着算法的运行速度.本文采用特征选择的方式从测试图像及训练图像集中选择区分性能高的特征用于分类识别，一方面提高了算法的运行速度，另一方面减少了算法的内存开销，为其应用于规模更大的图像库中提供了可能.算法基于特征的统计分布性质度量特征间的相关性并进行特征选择，计算公式如下所示:

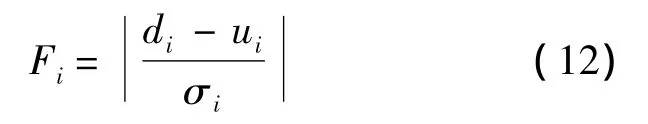
式中，ui表示特征的均值;σi表示特征的方差.通过实验发现，Fi在一定程度上度量了特征的区分性能，其数值越高表明特征的区分性能越高，其数值越低则表明区分性能越低.结合上述分析，本文提出的快速NBKNN算法可以描述为:

1)提取测试图像与C类训练图像中的局部特征，分别记为di∈Q和dCi.

2)根据式(12)计算测试图像和训练图像集中特征的Fi值，保留前M个最大Fi值对应的特征，其中测试图像中的前M个特征记为dM.

3)对每个dM在类别C中搜索其K近邻，分别记为{NC1，NC2，…，NCK}，在其他类别中搜索其最近邻并计算其均值

4)计算dM到各类别K－1近邻的距离之和，以及第K近邻及的距离，分别记为

5)对每个dM在各类别C中计算TC，TC=D1－D2－ D3，最 终 的 分 类 决 策 为:C^=

4 实验结果与分析

4.1 实验设置

为了验证本文所提算法的有效性，选择在Caltech-101图像库和Caltech-256图像库中进行分类识别实验，其中Caltech-101图像库包含了101种类型的图像，如动物、家具、车辆、花朵等类别，每类图像包含31～800张图像.Caltech-256图像库包含了256种类型的图像，每类包含至少80张图像.相比于 Caltech-101图像库，Caltech-256图像库更具复杂性.实验采取图像分类领域中的一般性做法，将图像集中的每类图像随机划分为训练图像集和测试图像集.与基于学习的分类方法不同，非参数化的分类算法没有学习的过程，因此不需要训练样本训练分类器，但是为了便于比较与表述，仍使用训练样本表示带有类别标签的参考图像，使用测试图像表示检索图像.本文采用稠密SIFT特征表示图像，提取特征的图像块大小为16×16，步长为8，实验中限制所有图像的长和宽不超过 300像素.特别地，本文采用FLANN进行近似近邻搜索，实验中设置随机KD-tree的个数为5.

4.2 Caltech-101图像库的实验结果

4.2.1 近邻个数K对分类性能的影响

首先衡量近邻个数K对分类性能的影响，实验中测试图像与训练图像均没有经过特征选择操作.实验结果如图1所示，当K取1时(不考虑背景信息的影响)本文算法退化为原始NBNN算法，图像分类正确率为62.32%.当K取10时，算法取得了最优分类性能，图像分类正确率达到65.18%，比原始 NBNN算法的正确率提高了2.86%.相比于原始NBNN算法，本算法在分类决策中充分利用了特征的K近邻信息并且去除了背景信息对分类的影响，因此分类性能较优.从实验结果还可以发现当K在相对较小的范围(5～20)中取值时，算法获得了相对较好的分类效果.K值过小，图像的分类性能较差;K值过大，分类性能并没有显著的提高，但在一定程度上增加了算法的复杂性.在文献［16］提出的LLC中，当最近邻个数K为5时取得最佳效果，本文实验结果与其具有一致性，在后续实验中取K=10.

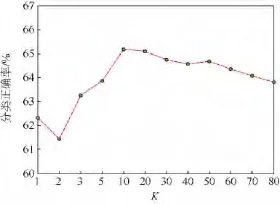
图1 近邻个数K对分类性能的影响Fig.1 Influence of number of nearest neighbors K for classification performance

表1给出了本文算法与其他一些分类算法的对比结果，从表中可以看出，在各种非参数化的分类算法中本文算法优于 SPM-NN，GB-NN［8］，GB Vote NN［22］，SVM-KNN［18］以 及 NBNN1 算 法，NBNN1表示仅仅使用SIFT特征的原始NBNN算法;但算法分类性能低于 Local NBNN和NBNN5［9］，NBNN5不仅使用了 SIFT 特征描述子，而且还结合了亮度、颜色、形状以及自相似描述子，因此能够更丰富、更加鲁棒地表示图像信息;Local NBNN算法选择局部近邻特征用于分类决策.虽然上述算法获取的分类性能较高，但也存在运行速度较慢、内存开销大等问题;表1中后4种算法是基于参数化分类算法的实验结果，算法包含了学习的过程.从实验结果可以看出，本文算法优于 SPM［5］，LLC［16］，NBNN-Kernel［10］，但分类性能低于 SCSPM［6］及 LSC［7］，LSC 采用局部软赋值编码的思想，这种思想与本文算法相似，充分利用了各邻域的信息，在一定程度上避免了量化过程中的信息损失，结合SVM分类器算法取得了较为理想的分类效果.虽然本文算法的分类性能低于ScSPM和LSC，但本算法不需要训练学习的过程，避免了学习过程中引起的诸多问题.

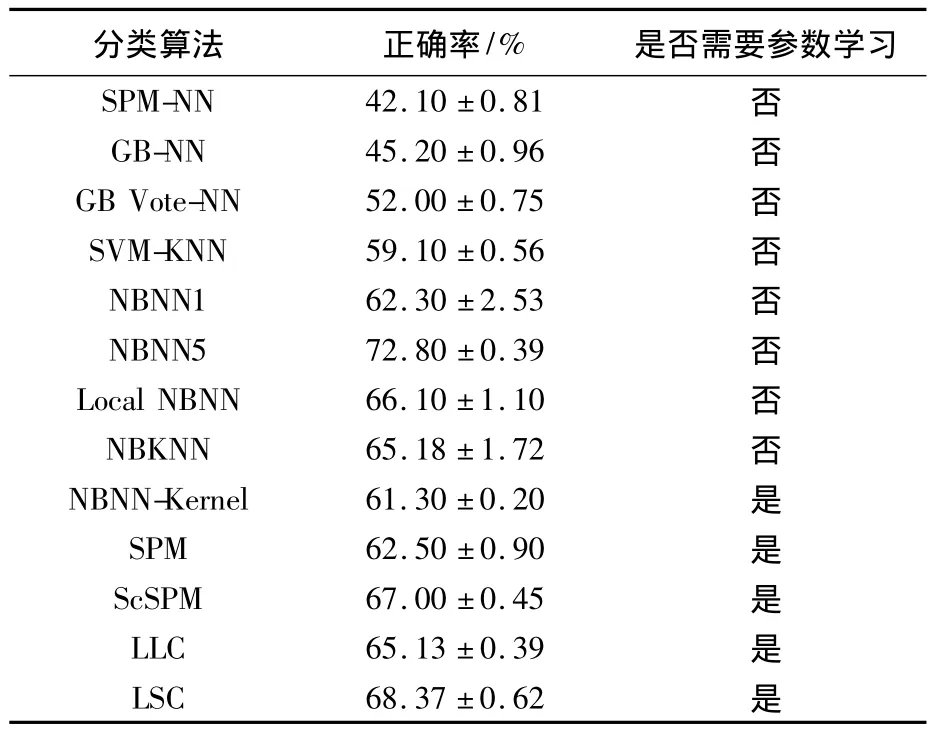
表1 不同算法在Caltech-101中的分类正确率比较Table1 Classification accuracy comparison on Caltech-101 of different algorithms

4.2.2 基于朴素贝叶斯K近邻的快速分类算法

原始NBNN算法运行速度慢，文献［9］给出在Caltech-101图像库中当训练样本个数为30时，采用NBNN算法对每张图像进行分类的平均时间约为140 s，当每类测试图像个数为15时，图像库共包含1 530张图像(共102类)，对所有图像进行分类所需时间约为59 h.本文上述实验中对每张图像进行分类的平均时间约为41 s，实验使用一台Core(TM)CPU 3.1 GHz，8 GB内存的计算机.对测试图像中的每个特征在训练图像集中搜索其最近邻并计算I2C距离占据着算法主要的运行时间，为了进一步提高算法的运行速度并减少近邻搜索中的内存开销，本文采用特征选择的方式分别减少测试图像、训练图像，并尝试同时减少二者中的特征数目，分析对分类性能的影响.

按照本文算法计算测试图像和训练图像集中各特征的Fi值并从大到小排序，分别保留测试图像和训练图像集中前90%，80%，…，10%的特征用于分类决策.NBNN主要的思想之一是采用I2C距离度量方式，因此需要提取训练图像集合中每幅图像的特征，并将所有图像的特征融合为一个整体再进行特征选择.实验结果如图2和图3所示，其中图2给出了不同情况下图像的平均分类正确率，图3给了相应情况下图像的平均分类时间，其中并不包括图像特征提取的时间.从实验结果可以看出，随着测试图像和训练图像集中特征的减少，图像的分类正确率均出现不同程度的下降，而运行速度越来越快.当选择测试图像90%和80%的特征用于分类决策时，图像分类正确率分别为63.75%和62.34%，平均分类时间分别为38.52 s和37.26 s;选择训练图像集90%和80%的特征时，图像分类正确率分别为64.14%和62.82%，平均分类时间分别为37.19 s和 33.41 s.上述方法在保证图像分类正确率的情况下，有效地降低了分类时间，均优于原始NBNN算法，特别是分类速度有了很大的提高.

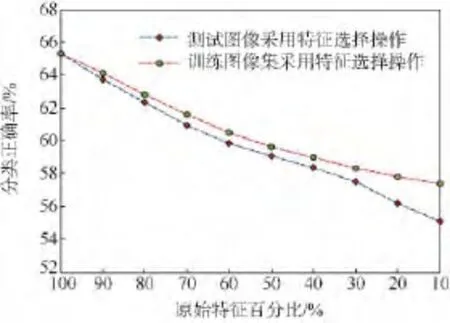
图2 Caltech-101中特征选择对分类正确率的影响Fig.2 Influence of feature selection for classification accuracy in Caltech-101

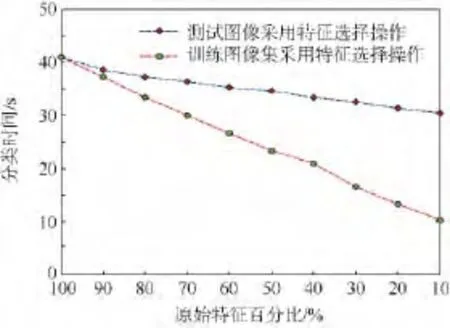
图3 Caltech-101中特征选择对分类时间的影响Fig.3 Influence of feature selection for classification time in Caltech-101

从图2可看出当测试图像和训练图像集分别选择相同特征数目百分比时，前者所获得的分类正确率均小于后者，并且当测试图像和训练图像集中的特征数目从100%降低到10%时，减少测试图像特征数目所引起图像分类正确率的下降多于训练图像集所引起分类正确率的下降，由此可见，在基于NBNN思想的图像分类中，减少测试图像中的特征对分类正确率影响较大;从图3可发现减少训练图像集中的特征对分类时间影响较大，随着训练图像集中特征数目的减少，算法的运行速度越来越快，主要原因是减少各类训练图像集(本实验中共102类)中的特征数目很大程度上减少了FLANN中索引的创建时间及最近邻搜索的时间.

以上分别通过特征选择的方式有效地减少了测试图像及训练图像集中的特征密度并分析了对分类性能的影响.通过实验结果可知，基于NBNN思想的图像分类算法应该尽可能地保留测试图像中的特征信息，虽然测试图像中包含了大量区分性能较低的特征，但是由于其数量较多，当把它们看作一个整体时仍然具有较强的区分性能;而对于训练图像集中的特征，应尽可能地去除那些信息量少的特征以及噪声点［23］.

基于上述实验分析，为了进一步提高算法的运行速度和减少算法的内存开销，尝试同时在测试图像和训练图像集中进行特征选择.为了保证算法的分类正确率，分别选择在测试图像90%和80%特征的情况下，逐渐减少训练图像集中的特征数目并比较图像的分类正确率和分类时间.为了表示方便，记原始测试图像与训练图像集的特征数目分别为NQ和NT，经过特征选择之后的特征数目分别为FQ和FT.图4和图5分别给出了两种情况下的实验结果，可以看出在训练图像库相同的情况下选择测试图像90%的特征用于分类可以获得较高的分类正确率，但其分类速度稍低于后者，这与理论分析相一致.当 FQ=90%NQ，FT=90%NT时，图像分类正确率为62.98%，分类时间为36.04 s，分类正确率虽然稍低于NBKNN算法，但其分类速度更快并且明显优于 NBNN算法.当 FQ=90%NQ，FT=80%NT及 FQ=80%NQ，FT=90%NT时图像分类正确率分别为62.02%和61.77%，分类时间分别为32.53 s和34.94 s，虽然分类性能稍低于原始NBNN算法，但是分类速度明显优于原始算法.因此选择合适的方式同时对测试图像和训练图像集进行操作可以平衡分类正确率和分类时间之间的矛盾，将最近邻分类器用于实际大规模图像分类任务中.

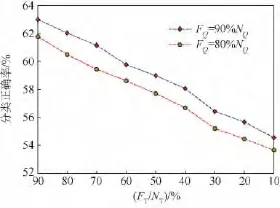
图4 Caltech-101中FQ=90%NQ与FQ=80%NQ时减少训练图像集特征数目对分类正确率的影响Fig.4 Influence of reducing feature numbers of training sets while FQ=90%NQand FQ=80%NQfor classification accuracy in Caltech-101

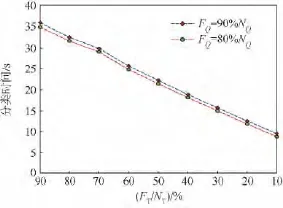
图5 Caltech-101中FQ=90%NQ与FQ=80%NQ时减少训练图像集特征数目对分类时间的影响Fig.5 Influence of reducing feature numbers of training sets while FQ=90%NQand FQ=80%NQforclassification time in Caltech-101

4.3 Caltech-256图像库的实验结果

为了进一步验证算法的有效性，本文在Caltech-256图像库上进行分类实验.在分类过程中分别从每类图像中随机选取15张图像作为训练图像和测试图像，每组实验分别执行5次，实验结果为数据集中所有类别图像的平均分类正确率.与前述实验设置相一致，当选取最近邻个数K为10时算法取得比较理想的分类正确率，后续实验中K的值均取10.表2给出了本文算法与其他一些分类算法在Caltech-256图像库上的结果.

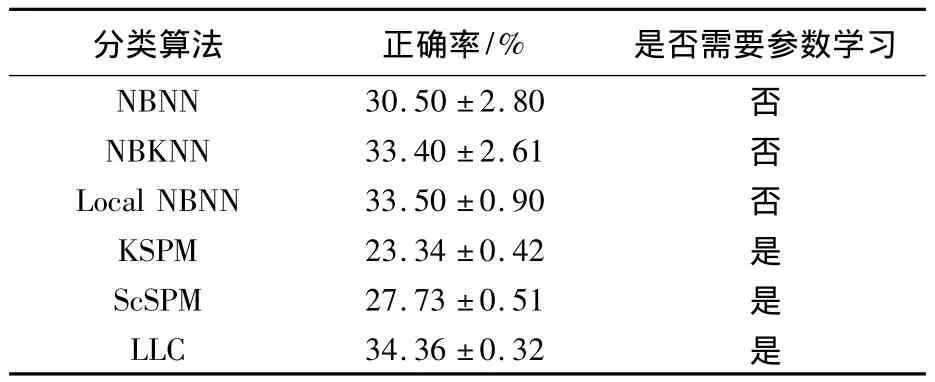
表2 不同算法在Caltech-256中分类正确率比较Table2 Classification accuracy comparison on Caltech-256 of different algorithms

从实验结果可以看出本文算法取得的分类正确率比原始NBNN算法提高了近3%，与Local NBNN算法取得的分类正确率相当.从表2还可以看出，非参数化分类算法在Caltech-256图像库上所取得的识别正确率普遍优于基于学习过程分类算法，主要原因是Caltech-256图像库包括了更多种类的图像，图像数据更加丰富，并且图像类内差距更加明显，变化更具多样性，在基于学习过程的分类算法中，训练器学习过程中容易产生过拟合等问题，并且上述算法中字典学习与特征编码等过程带来了一定的量化误差，从而影响了最终的分类正确率.

对规模更大的Caltech-256图像库进行分类所需时间更长，并且在近邻搜索中占用了大量的内存空间，因此这种局限性限制了基于NBNN思想的分类方法在实际大规模甚至中等规模图像库中的应用.采用本文提出的快速NBKNN算法分别计算测试图像和训练图像集中各特征的Fi值并从大到小排序，分别保留测试图像和训练图像集前90%，80%，…，10%的特征用于分类决策.实验结果如图6和图7所示，其中图6给出了不同情况下图像的平均分类正确率，图7给了相应情况下图像的平均分类时间.从实验结果可以看出减少测试图像中的特征对分类正确率影响较大，减少训练图像集中的特征对分类时间影响较大，这与前面实验结果分析相一致.

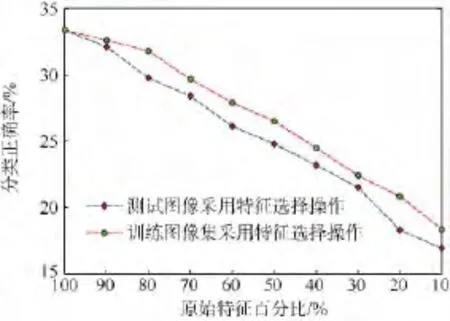
图6 Caltech-256中特征选择对分类正确率的影响Fig.6 Influence of feature selection for classification accuracy in Caltech-256

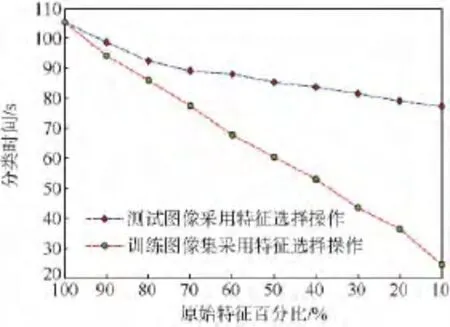
图7 Caltech-256中特征选择对分类时间的影响Fig.7 Influence of feature selection for classification time in Caltech-256

为了进一步提高算法的运行速度和减少算法的内存开销，尝试同时在测试图像和训练图像集中进行特征选择.为了保证算法的分类正确率，分别选择在测试图像90%和80%特征的情况下，逐渐减少训练图像集中的特征数目并比较图像的分类正确率和分类时间，实验结果如图8和图9所示.当 FQ=90%NQ，FT=90%NT时，图像分类正确率为32.21%，分类时间为92.21 s，分类正确率与分类速度明显优于 NBNN算法.当 FQ=90%NQ，FT=80%NT及 FQ=80%NQ，FT=90%NT时图像分类正确率分别为 31.28%和30.59%，分类时间分别为 83.71 s 和 88.20 s，分类性能与NBNN算法相接近，但是分类速度明显优于原始算法.

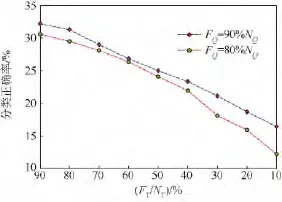
图8 Caltech-256中FQ=90%NQ与FQ=80%NQ时减少训练图像集特征数目对分类正确率的影响Fig.8 Influence of reducing feature numbers of training sets while FQ=90%NQand FQ=80%NQfor classification accuracy in Caltech-256

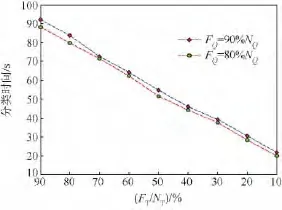
图9 Caltech-256中FQ=90%NQ与FQ=80%NQ时减少训练图像集特征数目对分类时间的影响Fig.9 Influence of reducing feature numbers of training sets while FQ=90%NQand FQ=80%NQfor classification time in Caltech-256

5 结论

本文在分析朴素贝叶斯分类算法的基础上，结合K近邻原理提出一种新的图像分类算法，经实验验证表明:

1)采用K近邻(K=10)用于分类决策并去除背景信息对分类正确率的影响，提高了原始NBNN算法的分类正确率;

2)针对NBKNN分类算法，比较分别在测试图像和训练图像集上采用特征选择的方式减少用于分类决策的特征数目对分类性能的影响，减少测试图像的特征数目对分类正确率影响较大，而减少训练图像集的特征数目对分类时间影响较大.

3)在NBKNN分类算法中选择测试图像90%的特征与训练图像集80%的特征用于分类决策，取得了与原始NBNN分类算法相近的分类正确率，但比原始NBNN算法快了近5倍，平衡了分类正确率与分类时间之间的矛盾，为最近邻分类器应用于实际提供了可能.

基于最近邻的图像分类算法与基于BoVW模型的图像分类算法各具优缺点，如何结合二者之间的优点在大数据背景下学习更有效、更合理的分类模型是本文后续工作的重点.

References)

［1］ Hong R，Wang M，Gao Y，et al.Image annotation by multiple-instance learning with discriminative feature mapping and selection［J］.IEEE Trans System，Man and Cybernetics Part:B，2014，44(5):669-680.

［2］ Hong R，Tang J，Tan H，et al.Beyond search:event driven summarization for web videos［J］.ACM Trans on Multimedia Computing，Communications，and Applications，2011，7(4):35-53.

［3］ Sivic J，Zisserman A.Video google:a text retrieval approach to object matching in videos［C］//Proceedings of the IEEE International Conference on Computer Vision.Piscataway，NJ:IEEE，2003:1470-1477.

［4］ Yang J，Jiang Y G，Hauptmann A G，et al.Evaluating bag-of-visual-words representations in scene classification［C］//Proceedings of the International Workshop on Workshop on Multimedia Information Retrieval.New York:ACM，2007:197-206.

［5］ Lazebnik S，Schmid C，Ponce J.Beyond bags of features:spatial pyramid matching for recognizing natural scene categories［C］//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2006，2:2169-2178.

［6］ Yang J，Yu K，Gong Y，et al.Linear spatial pyramid matching using sparse coding for image classification［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2009:1794-1801.

［7］ Liu L，Wang L，Liu X.In defense of soft-assignment coding［C］//Proceedings of the IEEE International Conference on Computer Vision.Piscataway，NJ:IEEE，2011:2486-2493.

［8］ Varma M，Ray D.Learning the discriminative power-invariance trade-off［C］//Proceedings of the IEEE 11th International Conference on Computer Vision.Piscataway，NJ:IEEE，2007:1-8.

［9］ Boiman O，Shechtman E，Irani M.In defense of nearest-neighbor based image classification［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2008:1-8.

［10］ Tuytelaars T，Fritz M，Saenko K，et al.The NBNN kernel［C］//Proceedings of the IEEE International Conference on Computer Vision.Piscataway，NJ:IEEE，2011:1824-1831.

［11］ Wang Z，Feng J，Yan S，et al.Linear distance coding for image classification［J］.IEEE Transactions on Image Processing，2013，22(2):537-548.

［12］ McCann S，Lowe D G.Local naive bayes nearest neighbor for image classification［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2012:3650-3656.

［13］ Yang X，Zhang T，Xu C.Locality discriminative coding for image classification［C］//Proceedings of the Fifth International Conference on Internet Multimedia Computing and Service.New York:ACM，2013:52-55.

［14］ Tommasi T，Caputo B.Frustratingly easy nbnn domain adaptation［C］//Proceedings of the IEEE International Conference on Computer Vision.Piscataway，NJ:IEEE，2013:897-904.

［15］ Wang Z，Hu Y，Chia L T.Improved learning of I2C distance and accelerating the neighborhood search for image classification［J］.Pattern Recognition，2011，44(10):2384-2394.

［16］ Wang J，Yang J，Yu K，et al.Locality-constrained linear coding for image classification［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2010:3360-3367.

［17］ Tuytelaars T，Schmid C.Vector quantizing feature space with a regular lattice［C］//Proceedings of the IEEE 11th International Conference on Computer Vision.Piscataway，NJ:IEEE，2007:1-8.

［18］ Zhang H，Berg A C，Maire M，et al.SVM-KNN:discriminative nearest neighbor classification for visual category recognition［C］//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2006，2:2126-2136.

［19］ Zhang H，Berg A C，Maire M，et al.SVM-KNN:discriminative nearest neighbor classification for visual category recognition［C］//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2006，2:2126-2136.

［20］ Rematas K，Fritz M，Tuytelaars T.The pooled NBNN kernel:beyond image-to-class and image-to-image［C］//Lecture Notes in Computer Science(Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics).Heidelberg:Springer Verlag，2013:176-189.

［21］ Muja M，Lowe D G.Fast approximate nearest neighbors with automatic algorithm configuration［C］//International Conference on Computer Vision Theory and Applications.Piscataway，NJ:IEEE，2009:331-340.

［22］ Berg A C，Malik J.Shape matching and object recognition［M］.Berlin Heidelberg:Springer，2006.

［23］ Hong R，Pan J，Hao S，et al.Image quality assessment based on matching pursuit［J］.Information Sciences，2014，273:196-211.