磁轴承PWM开关功放电流实时降噪

汤恩琼，房建成*，韩邦成

(1.北京航空航天大学仪器科学与光电工程学院，北京100191;2.北京航空航天大学惯性技术重点实验室，北京100191)

由于磁轴承具有转速高、无磨损、无需润滑、振动可控和动态特性可调等突出优点，已经成为磁悬浮控制力矩陀螺和飞轮等航天器执行机构［1-2］.而受PWM调制电路开关噪声、电磁噪声、电子元器件热噪声以及进入传感器的外部干扰信号等的影响，使得磁轴承PWM开关功放电流含有大量噪声，从而严重影响到磁悬浮转子的控制精度和稳定性［3］.

对于信号去噪，通常情况下，由于噪声能量一般集中于高频，可以通过低通滤波器进行滤波，从而达到消除高频噪声信号的目的.这种方法在有效信号和噪声信号的频带相互分离的时候能够获得比较好的去噪效果，但是当有效信号和噪声信号的频带相互重叠时，则效果较差.

近十多年来，小波分析的理论在故障诊断、信号去噪、图像处理等专业领域得到了广泛的应用［4-7］.与第一代小波变换相比，提升小波变换具有许多优良的特性:结构简单、运算量低、原位运算、节省存储空间、逆变换能够直接反转实现.更重要的是，通过选择合适的小波分解层数，可以达到在对系统带宽影响较小的情况下实现对信号的有效降噪［8］.

文献［9］用非抽样提升小波包及奇异值分解相结合的降噪方法对液阀故障微弱信号进行降噪处理，最终获得了获得较高的信噪比，且能较好地保留高频信号;文献［10］针对传统的自适应方向提升小波变换(ADL-DWT)算法在高分辨率遥感影像压缩中计算复杂度过高的问题，提出一种新的基于方向预测的提升小波变换(DP-LWT)算法，实现了高分辨率遥感影像的快速、高效压缩;文献［11］通过将提升小波变换和Sobel-Tenengra算子有机组合提出了一种新型聚焦评价函数，大大提高了聚焦速度且性能稳定，满足了显微视觉自动聚焦要求，获得了良好聚焦效果.以上文献虽然也是采用提升小波实现信号的信噪分离，但是都是在离线状态下进行的，并不能对信号进行实时降噪并反馈滤波结果.因此为了实现对信号的实时降噪，文献［12］通过采用滑动数据窗的方式，构造出实时小波降噪仿真证明实时降噪的效果;文献［13］基于提升小波算法，提出了一种结合硬阈值、强制降噪和带滑动数据窗的实时降噪方案，实现了对光纤陀螺信号的实时去噪，计算速度快，效果明显.

本文基于dB4提升小波算法，采用滑动数据窗、对称边界拓展和阈值降噪相结合的方案实现了对磁轴承PWM开关功放电流的实时降噪.实验证明了提升小波实时降噪法的有效性.

1 PWM开关功放系统

磁轴承PWM开关功放系统如图1所示.PWM开关功放产生的控制电流信号主要由4个MOSFET(G1，G2，G3，G4)按一定的工作方式导通或者关断来实现.导致PWM开关功放参考输入信号变化率增大的因素主要有:转子位移的同频振动信号、转子传感器检测面不光滑产生的位移倍频信号以及功放电流中所包含的噪声信号［14-15］.前者可以通过在控制回路中串接同频陷波器得以消除，而功放噪声不仅存在于高频段，而是分布在整个频率段.因此仅使用低通滤波器不但难以达到最优的滤波效果，还会降低功放电流的跟踪速度和带宽，增加系统的相角滞后，从而影响系统稳定性.本文拟采用提升小波变换对功放电流进行降噪，实验证明了该方法的有效性.

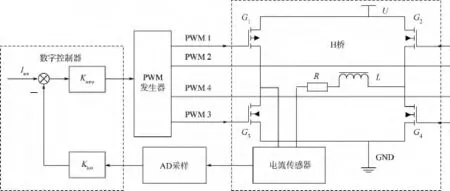
图1 磁轴承PWM开关功放系统Fig.1 PWM switching amplifier of magnetic bearing system

2 提升小波变换

提升小波变换降噪法完全抛弃了傅里叶变换和传统小波变换把信号变换到频域分析的方法，只在时域对信号进行去噪处理，大大减少了算法运算的时间，能够满足嵌入式设备等对实时性和应用性的要求.小波变换的提升实现主要由分解、预测和更新3部分组成.

1)分裂.

将原始的离散信号x［n］分解为2组相互关联的部分，通常分解为奇样本和偶样本.即

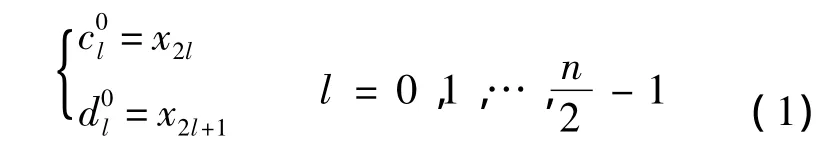
2)预测.

预测过程又称为对偶序列提升过程.构造预测算子P(·)，用偶数组c0l预测奇数组d0l，得到预测的偏差信号结果为小波系数，即

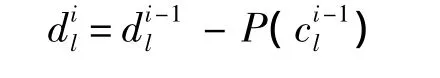
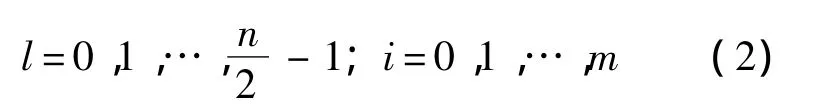
3)更新.

更新过程又称为提升过程.用小波系数及更新算子U(·)对偶序列进行更新，其结果为尺度系数.更新也被视为低通滤波器对信号进行的平滑操作，处理后的信号比前一尺度具有更少的高频成分.

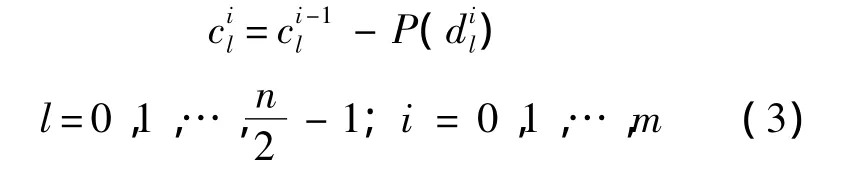
通过上述3个步骤就完成了一个提升过程.从提升的过程可以看出，基于提升方法的小波变换能够实现原位运算，而不需要除前一级提升过程的输出以外的数据，在每一位上都能用新的数据点来替换旧的数据点.

提升小波变换的重构由恢复更新、恢复预测、奇偶样本合并3步构成，其重构公式由式(2)、式(3)逆变换可得.提升小波变换的分解与重构过程如图2所示.

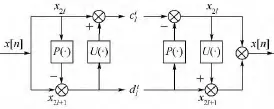
图2 提升小波变换的分解与重构过程Fig.2 Decomposition and reconstruction of lifting wavelet transformation method

3 实时降噪方案

传统的小波去噪方法多用于数据的离线处理，而PWM开关功放电流的实时去噪则需要兼顾信号降噪性能和数据处理速度.与信号的离线处理不同，在实际系统中为满足实时降噪要求，小波实时降噪处理的信号点数远小于PC机离线信号分析所使用的信号点数，以保证系统降噪处理的实时性.

因此，实时降噪采用滑动数据窗的方式取数，具体实现方式如图3所示.在 t0时刻，将当前采样数据x8与过去7采样周期采样得到的数据x1～x7按顺序组成一维数组，并向右进行对称周期扩展，然后用提升小波算法对其进行去噪处理，最终生成了8个新数据 x'1～x'8.其中x'8即为小波去噪算法对当前时刻的采样数据x8滤波之后的结果.t1时刻，AD采样得到新的原始数据x9，此时先将x'2～x'8在一维数组中分别左移一个位置，去掉x'1，并将x9补充到x'8空出的位置，组成新的8元素一维数组，然后再次对其进行边界扩展并执行小波变换算法，重复以上步骤，便可以实现提升小波算法对功放电流采样数据的实时降噪.

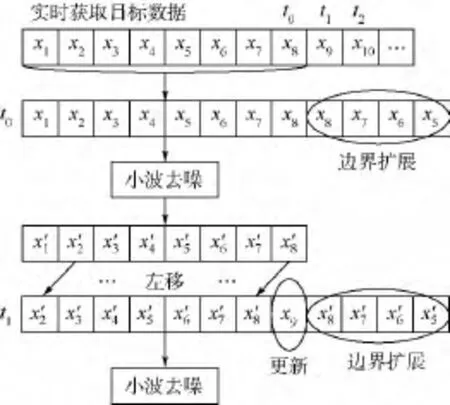
图3 滑动数据窗原理Fig.3 Sliding data window

此外，本文采用软阈值法进行降噪处理.软阈值收缩方法如下:

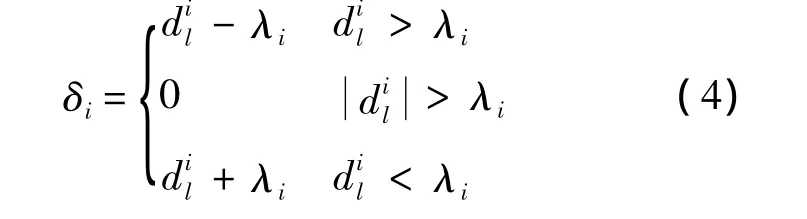
式中λi为第i层阈值，与参与处理的数据数量N和数据中的噪声水平有关，可以根据统计分析确定.为了简化应用，可以采用通用阈值法计算阈值:

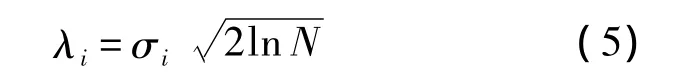
式中σi为第i层噪声信号的标准差，其值的计算方法是取小波系数在各个尺度下绝对值的中值，然后将该中值除以常数0.6745作为该尺度下小波系数中噪声强度的估计，即

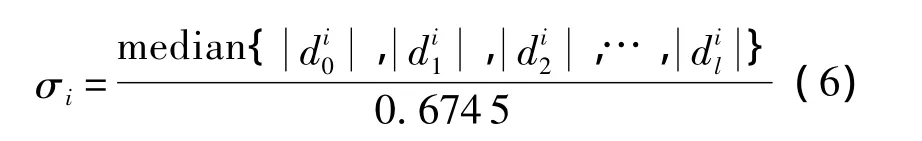
式中median{·}为取中值计算.

由于磁轴承PWM开关功放带宽为790 Hz，而系统采样频率为6667Hz，所以兼顾考虑降噪效果和功放带宽，选择小波分解层数为2层，则小波分解后得到的低频小波系数截止频率为834 Hz.

4 实验分析

本文采用dB4小波对PWM开关功放电流进行实时降噪处理，其提升算法实现方式如下:

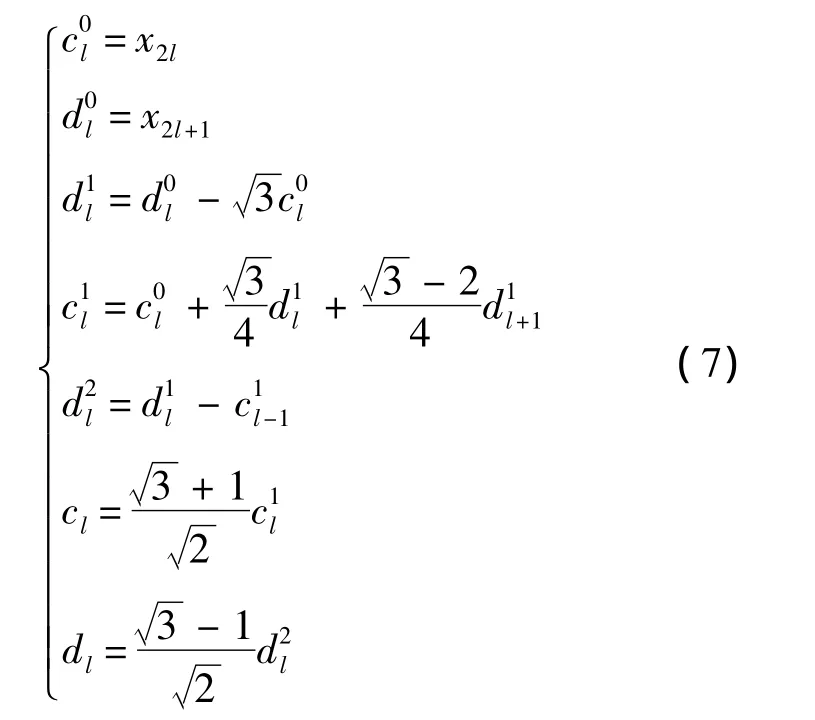
重构算法可由式(7)的逆变换得到.

实验用的磁悬浮电机及其控制系统如图4所示.控制器采用DSP+FPGA的综合控制方式，AD采样周期为150 μs，PWM 载波周期为 20 kHz，功放电压为60 V，线圈电感为22 mH，线圈等效电阻约为1 Ω，偏置电流为1 A，转子质量为20 kg.

根据前文分析，选择分解深度为2层，滑动数据窗宽度为8，边界采用对称周期延拓扩展，单边扩展长度为4，第1层阈值为0.2606，第2层阈值为0.352 9.在转子转速10 000 r/min时启用提升小波算法，测得功放电流及其频谱分别如图5(a)和图6(a)所示.同时，为了与传统的滤波器滤波效果进行比较，选择截止频率同样为834Hz的2阶低通滤波器对采样数据进行滤波，滤波器形式如下:

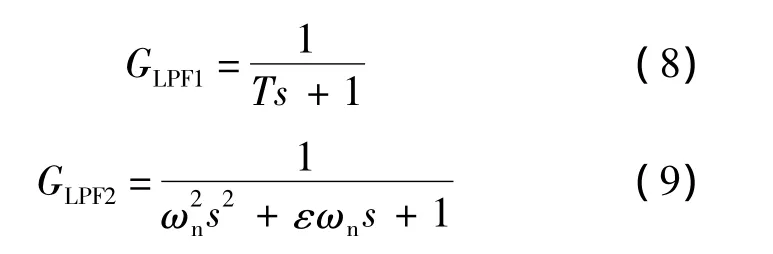
其中，T=ωn=2π·834;ε =0.707.滤波效果及滤波后电流频谱分别如图5(b)、图5(c)和图6(b)、图6(c)所示.通过图6电流信号频谱对比可以看出，采用阈值法强制去噪，小波变换可以有效地去处信号中的噪声，且降噪效果明显优于传统的低通滤波器.

图4 磁悬浮电机及其控制系统Fig.4 Magnetically suspended motor and its control system

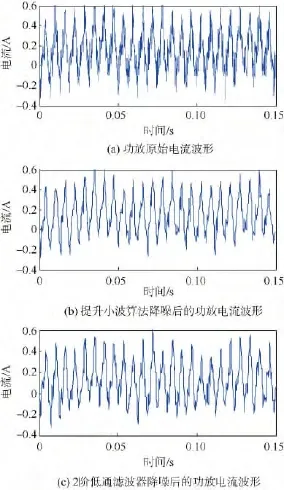
图5 不同方式下的功放电流降噪效果对比Fig.5 De-noising results of amplifier current with different methods

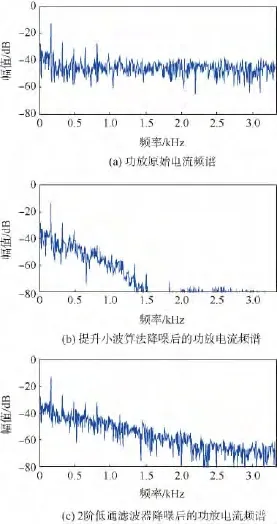
图6 不同滤波方式滤波后的功放电流频谱对比Fig.6 De-noising results of amplifier current spectrum with different methods

为定量评价降噪效果，引入两个指标:信噪比和均方差.信噪比越大，均方差越小，说明降噪效果越好.不同滤波算法的信噪比和均方差，可以通过在转子静态悬浮时施加正弦激励信号进行测试.正弦输入信号作为标准信号x(k)，滤波后信号为(k)，计算结果如表1所示.可从结果看出，提升小波实时降噪法滤波效果要明显优于传统的数字低通滤波器.

表1 不同滤波算法信噪比和均方差对比Table1 Comparison of the SNR and root mean square error(RMSE)with different filtering methods

采用提升小波算法对转子进行升速实验，并随机选取部分转速下滤波效果进行对比.图7(a)和图7(b)分别为转子转速5 000 r/min和额定转速20000 r/min条件下，在t=0.75 s时启用提升小波滤波前后功放电流波形对比.实验证明提升小波滤波算法在转子的整个升速过程中，都可以起到非常好的滤波效果.

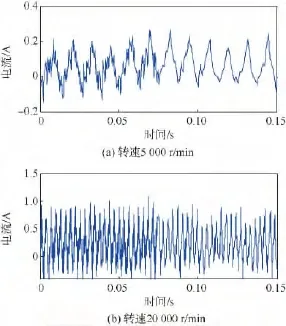
图7 不同转速下提升小波滤波前后的功放电流波形对比Fig.7 Amplifier current before and after using lifting method at different rotational speed

5 结论

本文采用提升小波变化实时降噪方法对磁轴承PWM开关功放进行去噪处理，经实验验证表明:

1)基于滑动数据窗处理的提升小波算法，可以实现对功放电流的实时降噪;

2)与传统的2阶低通滤波器相比，采用提升小波实时降噪法对功放电流进行降噪，在信噪比上有6.62 dB的提升;

3)提升小波降噪法可以有效降低电流噪声，且对低频段的信号衰减较小.

References)

［1］ 韩邦成，崔华，汤恩琼.基于滑模扰动观测器的磁轴承主动振动控制［J］.光学精密工程，2012，20(4):563-570.Han B C，Cui H，Tang E Q.Vibration suppression of magnetic bearing based on sliding mode disturbance observer［J］.Optics and Precision Engineering，2012，20(4):563-570(in Chinese).

［2］ 汤继强，韩雪飞，刘强.微框架效应磁悬浮飞轮转子轮缘优化设计［J］.光学精密工程，2012，20(9):1991-1998.Tang J Q，Han X F，Liu Q.Optimal design of rotor rim for magnetically suspended flywheel with vernier gimballing capacity［J］.Optics and Precision Engineering，2012，20(9):1991-1998(in Chinese).

［3］ Gerhard S，Eric H M.Magnetic bearings:theory，design，and application to rotating Machinery［M］.Berlin:Springer-Verlag，2009.

［4］ 胡桥，何正嘉，张周锁.基于提升小波包变换和集成支持矢量机的早期故障智能诊断［J］.机械工程学报，2006，42(8):17-22.Hu Q，He Z J，Zhang Z S.Intelligent diagnosis for incipient fault based on lifting wavelet package transform and support vector machines ensemble［J］.Chinese Journal of Mechanical Engineering，2006，42(8):17-22(in Chinese).

［5］ 谢全民，龙源，钟明寿.SGWT在爆破振动信号信噪分离中的应用研究［J］.振动与冲击，2012，31(1):24-28.Xie Q M，Long Y，Zhong M S.Application of SGWT in separation of noises from a blast vibration signal［J］.Journal of Vibration and Shock，2012，31(1):24-28(in Chinese).

［6］ 刘荣科，张晓林，廖小涛.基于可逆提升小波变换和上下文预测的SAR图像无损压缩算法［J］.航空学报，2002，23(6):534-537.Liu R K，Zhang X L，Liao X T.Lossless image coding algorithm for SAR based on reversible lift schematics comined with context predictor［J］.Acta Aeronautica et Astronautica Sinica，2002，23(6):534-537(in Chinese).

［7］ 陈升来，黄廉卿，郭静寰.基于整型提升小波变换的图像处理及 DSP 实现［J］.光学精密工程，2013，21(3):498-502.Chen S L，Huang L Q，Guo J H.Image processing based on integral lifting scheme and its implementation by DSP［J］.Optics and Precision Engineering，2013，21(3):498-502(in Chinese).

［8］ 沈晓卫，姚敏立，常瑞花.模糊逻辑提升小波在惯性传感器去噪中的应用［J］.振动与冲击，2011，30(12):226-234.Shen X W，Yao M L，Chang R H.Application of fuzzy logic and lifting wavelet transformation in de-noising of inertial sensors［J］.Journal of Vibration and Shock，2011，30(12):226-234(in Chinese).

［9］ 陈敬龙，张来斌，段礼祥，等.基于非抽样提升小波包及奇异值分解的液阀故障诊断［J］.机械工程学报，2011，47(9):72-77.Chen J L，Zhang L B，Duan L X，et al.Diagnosis of liquid valve based on undecimated lifting scheme packet［J］.Chinese Journal of Mechanical Engineering，2011，47(9):72-77(in Chinese).

［10］ 张立保，丘兵昌.基于快速方向预测的高分辨率遥感影像压缩［J］.光学精密工程，2013，21(8):2095-2102.Zhang L B，Qiu B C.Remote sensing image compression based on fast direction prediction［J］.Optics and Precision Engineering，2013，21(8):2095-2102(in Chinese).

［11］ 周丽平，孙志峻，张泉.显微视觉系统的自动聚焦及控制［J］.光学精密工程，2013，21(3):807-812.Zhou L P，Zhang Z J，Zhang Q.Auto focusing and control of micro-vision system［J］.Optics and Precision Engineering，2013，21(3):807-812(in Chinese).

［12］ 蒋东方，陈明.一种实时小波降噪算法［J］.仪器仪表学报，2004，25(6):781-783.Jiang D F，Chen M.A real-time wavelet de-noising algorithm［J］.Chinese Journal of Scientific Instrument，2004，25(6):781-783(in Chinese).

［13］ 高伟，祖悦，王伟.基于二代小波的光纤陀螺实时降噪方法研究［J］.仪器仪表学报，2012，33(4):774-780.Gao W，Zu Y，Wang W.Research on real-time de-noising of FOG based on second generation wavelet transform［J］.Chinese Journal of Scientific Instrument，2012，33(4):774-780(in Chinese).

［14］ Kyungdae K，Alan P.Homopolar magnetic bearing saturation effects on rotating machinery vibration［J］.IEEE Transactions on Magnetics，2012，48(6):1984-1994.

［15］ 张德魁，赵雷，赵鸿宾.电流响应速度及力响应速度对磁轴承系统性能的影响［J］.清华大学学报:自然科学版，2001，41(6):23-26.Zhang D K，Zhao L，Zhao H B.Effect of current response rate and force response rate on performance of magnetic bearing systems［J］.Journal of Tsinghua University:Science and Technology，2001，41(6):23-26(in Chinese).