基于运动约束的脉冲雷达游标测距方法

陈浩，郭军海，齐巍

(北京跟踪与通信技术研究所，北京100094)

随着靶场对脉冲雷达测距测速精度要求的越来越高，脉冲雷达高精度测距测速技术成为研究的热点.国外实现的高精度测距技术是一种称为距离游标的相位测距技术.距离游标技术［1-2］是美国于20世纪70年代发展起来的一种应用于全相参脉冲多普勒雷达的高精度相位测距技术.中国曾在20世纪80年代组织了相关领域的专家研究窄带游标测距技术，但仅作了仿真分析，并没有在实测数据上进行验证.在利用距离游标方法进行脉冲雷达测距过程中，需要利用测速系统得到的多普勒频率解多普勒相位增量模糊.而低重频脉冲雷达存在严重的速度模糊［3-4］，常用的解速度模糊方法有多重频解模糊和基于距离微分的解模糊方法.最常用的多重频方法为中国剩余定理方法(CRT)［5-6］，但CRT方法最大的缺点是对噪声极度敏感.为了解决噪声敏感的问题，Trunk等提出了改进的CRT方法［7-8］，但为了解速度模糊，对脉冲重复频率有特殊的要求.根据多重频脉冲雷达信号频谱的稀疏特性，文献［9］和文献［10］将压缩感知理论［11］应用于多重频脉冲雷达解速度模糊.该方法比CRT方法对噪声更具有鲁棒性，但为了正确解速度模糊，需要构造冗余度很大的稀疏字典，导致计算量过大，不具有实用性.利用距离微分方法来解速度模糊是工程上常用的方法.而通常采用的“不变量”嵌入法［12］要求距离微分精度优于fr/2(fr为脉冲重复频率)，利用脉冲测距法不一定能满足这个精度要求.我国目前在工程上无法实现距离游标技术的一个重要原因是不能解决这种解速度模糊和解相位模糊相互耦合的问题.

本文将目标的运动约束应用到距离游标方法中，提出一种同时解速度模糊和解相位模糊的耦合滤波器.利用目标的运动约束积累一段时间的测量数据进行UKF滤波［13］估计得到精度较高的速度解速度模糊，从而启动耦合滤波器.然后利用无模糊的速度进行距离游标，再把距离游标得到的距离应用于下一时刻的速度并解速度模糊，一次进行下去把距离游标与多普勒测速耦合在同一个滤波器里面.

1 解相位模糊与解速度模糊耦合

1.1 距离游标基本原理

游标测距方程为:游标距离=基准距离+相对距离，其中的基准距离由雷达的测距系统得到，相对距离由相位测距方法得到.定义发射信号与回波信号的瞬时相位差为多普勒相位θd(t).通过计算相邻回波间的多普勒相位增量:

式中，εi为通过I/Q回路测量得到的多普勒相位测量误差;θi，θd(i)为多普勒相位真值.

式中t′i为第i个脉冲的回波时刻，可得到相位增量估计值，利用正确解相位模糊的前提条件可解相位模糊.

1.2 多普勒测速原理

当目标在雷达视线方向产生相对运动时，会产生多普勒效应.令产生的多普勒频率为Fd，则多普勒频率与径向速度的关系为

式中，vr为目标的径向速度;λ为发射脉冲波长.因此，对目标速度的测量可转化为对多普勒频率的测量，精密测量采用闭环测量法，用窄带跟踪滤波器和二阶环路实现.

低重频脉冲雷达测速回路可能跟踪在信号频谱上的任一根细谱线上，此时测出的多普勒频率存在模糊:

式中，L为模糊谱线数;fd为模糊多普勒频率;Fd为无模糊多普勒频率.因此需要通过解模糊来得到无模糊的多普勒频率.

2 基于运动约束的耦合滤波器

2.1 问题分析

高动态目标的距离游标本质上也是高机动目标跟踪问题［14］，可建立机动目标模型，利用脉冲雷达量测数据(若利用单台脉冲雷达进行距离游标，量测数据为径向距离R，方位角A和俯仰角E)进行自适应滤波.将自适应滤波得到的目标运动特征应用到距离游标里面.即根据机动目标跟踪模型，建立基于目标运动约束的距离游标算法.常用的机动目标模型有参数回归模型、运动学模型和动力学模型［15］.其中常用的参数回归模型有多项式模型和样条函数模型，常用的运动学模型有常速(CV)模型、常加速度(CA)模型及“当前”统计(CS)模型［16］等.根据目标不同的运动特征，可选择不同的运动模型建立相应的运动约束，将模型先验信息用于融合估计，以更有效地提高估计精度.对于导弹自由段和卫星目标等，由于目标运动特征更为接近二体运动，能建立较为准确的动力学模型，选用动力学模型较为合适［17］.对于机动较小的目标，可选择CV模型和CS模型.对于导弹主动段等机动性较强且受力较为复杂，可建立CS模型来提供运动约束.对于CS模型，设状态向量X=(x，，y，，z，)T，则

式中，W(k)为状态噪声序列;T为状态转移时间间隔.

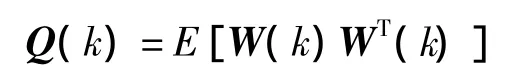
测量方程为

式中Y(k)为各测量设备测量元素组成的向量，Y(k)=［A1(k)，…，An(k)，E1(k)，…，Rn(k)，R1(k)，…，Rn(k)］，各测元的测量方程如下:

2.2 耦合滤波器流程

针对相位测距解模糊和多普勒测速相互耦合的问题，本文设计了一种迭代耦合滤波器(见图1)，可以同时解相位模糊和多普勒速度模糊.其基本思路为:对于高动态目标，利用文献［18］提出的加速度估计算法准确估计目标加速度，进行加速度补偿后可准确估计目标的模糊速度.再积累一段时间(t－L+1，t－L+2，…，t0时刻)脉冲雷达测量数据(脉冲测距得到的径向距离、方位角A和俯仰角E)利用运动约束(动力学方程或运动学方程)进行UKF滤波可得到t0和t1时刻的径向速度和，并以 t0时刻滤波得到的径向距离作为距离游标的基准距离.结合得到的高精度的模糊速度可解速度模糊，得到无模糊的多普勒速度v0和v1.利用无模糊的v0和v1可以解多普勒相位增量模糊，从而得到t0和t1时刻的距离增量ΔR0，1和游标距离R1.用游标距离R1替代脉冲测距径向距离R1并利用UKF滤波作一步预测得到t2时刻的径向速度，用和模糊多普勒速度可得到无模糊的多普勒速度v2.利用无模糊的多普勒速度v1和v2可以解多普勒相位增量模糊，从而得到t1和t2时刻的距离增量ΔR1，2和游标距离R2.用游标距离 R2取代测量量可继续进行UKF滤波得到下一时刻的速度并解速度模糊，距离游标可继续进行下去.为了增加算法的稳健性，令=ΔRL，L+1/T，利用文献［6］中提出的解模糊纠错判断方法对是否正确解多普勒相位增量模糊进行判断.

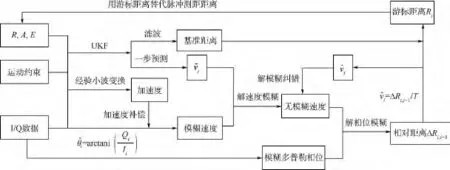
图1 耦合滤波器图Fig.1 Diagram of coupled filter

3 理论仿真与实测数据验证

3.1 理论仿真

脉冲雷达参数选取为某经典单脉冲测量雷达，脉冲重复频率fr=292 Hz，发射脉冲频率为f0=5596 MHz，脉冲宽度 T=44.5 μs.选取的数据为某导弹主动段的径向距离R、方位角A和俯仰角E，分别在测量数据上添加相应的测量误差以仿真测量数据.输入I/Q信号信噪比为12 dB，当信号信噪比为12 dB时，单脉冲测距误差为6.12 m，方位角、俯仰角测角误差均为 5 mrad，利用I/Q信号得到的多普勒相位测量噪声为10.44°(包括接收机噪声，模拟正交解调的幅相噪声和量化误差)，多普勒频率误差为6 Hz.

针对主动段数据选取的是“当前”统计模型，并利用UKF滤波对数据进行积累以提高径向速度的精度以及正确解速度模糊，从而启动迭代耦合滤波器.图2为用本文方法和传统距离游标方法得到的相对距离误差.图3(a)为利用运动约束的距离游标算法得到的径向距离误差，图3(b)为利用脉冲测距得到的径向距离误差，其中脉冲测距的随机误差为6.0366 m，本文方法的随机误差为0.075 8 m.从图中可以看出，本文的方法能克服测距精度不高导致速度模糊与相位模糊相互耦合的问题，而传统距离游标方法会出现解相位模糊出错的情况导致距离误差发生积累.从图3可以看出本文的方法大大减小了径向距离随机误差，从米级降至厘米级.

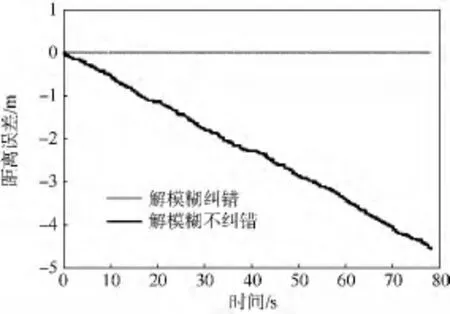
图2 传统距离游标与本文方法距离误差对比Fig.2 Comparison of range error of traditional Vernier ranging method and method of this paper

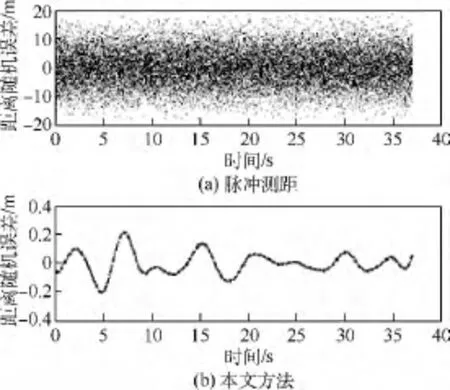
图3 脉冲测距与本文方法得到的距离随机误差Fig.3 Random range error obtained by pulse ranging method of this paper

3.2 实测数据验证

利用某型C波段雷达校飞数据进行距离游标，用匀速运动(CV)模型进行运动约束，用本文的基于运动约束的距离游标算法进行验证，将得到的游标距离与GPS测得的目标径向距离作比对.比较游标测距与脉冲测距测得的目标径向距离误差和随机差.图4为两种测距方法的随机误差对比，图5为游标测距的随机误差.图6为两种测距方法测得距离与GPS数据比对后得到的距离误差对比.距离游标径向距离随机误差均方根误差为0.0685 m，脉冲雷达脉冲测距随机误差均方根误差为1.1996 m.

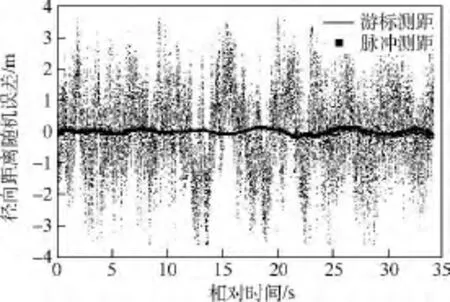
图4 飞机跟踪数据游标测距与脉冲测距随机误差对比Fig.4 Random range error comparison of pulse ranging method and method of this paper on measured data of airplane

图5 飞机跟踪数据游标测距随机误差Fig.5 Random range error of Vernier range on measured data of airplane

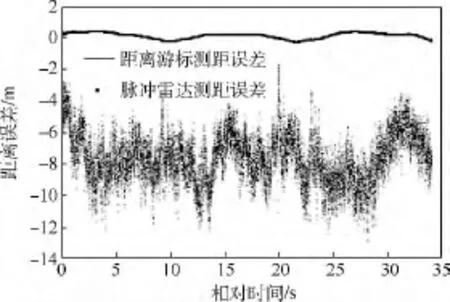
图6 飞机跟踪数据游标测距与脉冲测距误差对比Fig.6 Random range error comparison of Vernier range and pulse range of measured data of airplane

对某型雷达测得的某卫星数据，用动力学模型进行运动约束，用本文的基于运动约束的距离游标算法进行验证，得到的径向距离随机误差如图7和图8所示，距离游标测距随机误差均方根误差0.086 9 m，雷达脉冲测距误差均方根误差1.3632 m.

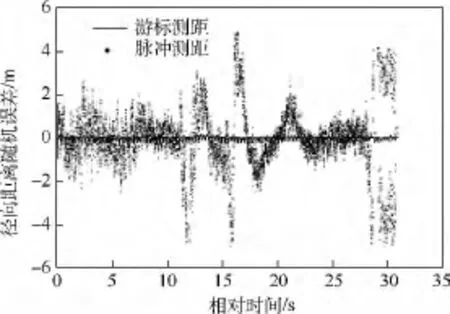
图7 卫星数据游标测距与脉冲测距随机误差对比Fig.7 Random range error comparison of pulse ranging method and method of this paper on measured data of satellite

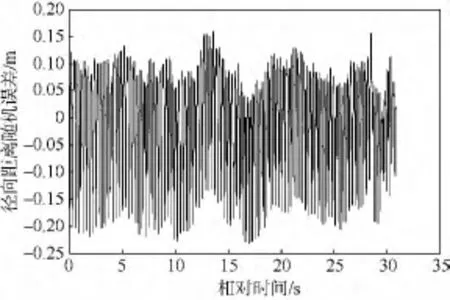
图8 卫星数据游标测距随机误差Fig.8 Random range error of Vernier range on measured data of satellite

通过实测校飞数据对本文算法验证可得，基于运动约束的距离游标算法能大大减小距离随机误差，将随机误差从米级降至厘米级.通过与GPS数据可以发现距离游标的测量误差要比脉冲测距测量误差小两个数量级.雷达测得的卫星数据也验证了本文算法的有效性，将随机误差减小两个数量级.

4 结论

本文提出了一种基于运动约束的距离游标算法，通过仿真和实测数据验证表明:

1)算法能克服相位模糊和速度模糊相互耦合的问题，大大减小了距离随机误差.

2)对高速飞行器主动段仿真数据可将距离误差减小至少一个数量级至分米级.

3)对LY3901雷达测得的卫星和飞机跟踪数据，该距离游标方法能将距离随机误差减小至少一个数量级至分米级.

References)

［1］ Russell Roy.Range Vernier:USA，ADA-077178［P］.1979-08-30.

［2］ Pickett R B.Ambiguious range study report:USA，ADA-048612［P］.1977-06-30.

［3］ 谢洁，杨文军，黎海林，等.低重复频率下的目标速度估计算法研究［J］.现代雷达，2010，32(9):36-39.Xie J，Yang W J，Li H L，et al.A study on target velocity estimation under low PRF condition［J］.Modern Radar，2010，32(9):36-39(in Chinese).

［4］ 刘一峰.游标测距原理研究及其在线性调频脉冲雷达数据处理中的应用［D］.南京:南京理工大学，2004.Liu Y F.Research on principles of Vernier ranging and its application on radar data process of linear frequency modulation radar［D］.Nanjing:Nanjing University of Science and Technology，2004(in Chinese).

［5］ Skolnik M I.Radar handbook［M］.3rd ed.New York:McGraw-Hill，2008:58-68.

［6］ Richards M A.Fundamentals of radar signal processing［M］.New York:McGraw-Hill，2005:141-154.

［7］ Trunk G，Brockett S.Range and velocity ambiguity resolution［C］//IEEE National Radar Conference.Piscataway，NJ:IEEE，1993:146-149.

［8］ Trunk G V，Kim M W.Ambiguity resolution of multiple targets using pulse-Doppler waveforms［J］.IEEE Transactions on Aerospace and Electronic Systems，1994，30(4):1130-1137.

［9］ Quan Y H，Zhang L，Xing M D，et al.Velocity ambiguity resolving for moving target indication by compressed sensing［J］.Electronics Letters，2011，47(22):1249-1251.

［10］ 张玉玺，孙进平，张冰尘，等.基于压缩感知理论的多普勒解模糊处理［J］.电子与信息学报，2011，33(9):2103-2107.Zhang Y X，Sun J P，Zhang B C，et al.Doppler ambiguity resolution based on compressive sensing theory［J］.Journal of Electronics and Information Technology，2011，33(9):2103-2107(in Chinese).

［11］ Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［12］ 王德纯，丁家会，程望东.精密跟踪测量雷达技术［M］.北京:电子工业出版社，2006:31-32.Wang D C，Ding J H，Cheng W D.Technologies of precision tracking radar［M］.Beijing:Electronic Industry Press，2006:31-32(in Chinese).

［13］ Julier S J，Uhlmann J K.Unscented filtering and nonlinear estimation［J］.Proceedings of the IEEE，2004，92(3):401-422.

［14］ 周宏仁，敬忠良，王培德.机动目标跟踪［M］.北京:国防工业出版社，1991:138-140.Zhou H R，Jing Z L，Wang P D.Tracking of maneuvering targets［M］.Beijing:National Defence Industry Press，1991:138-140(in Chinese).

［15］ 郭军海.弹道测量数据融合技术［M］.北京:国防工业出版社，2012:140-142.Guo J H.Missile trajectory measurement and data fusion technology［M］.Beijing:National Defence Industry Press，2012:140-142(in Chinese).

［16］ Li X R，Jilkov V P.A survey of maneuvering target trackingpart I:dynamic models［J］.IEEE Transactions on Aerospace and Electronic System，2003，39(4):1333-1351.

［17］ Li X R，Jilkov V P.A survey of maneuvering target trackingpart II:motion models of ballistic and space targets［J］.IEEE Transactions on Aerospaceand ElectronicSystem，2010，39(4):96-114.

［18］ 陈浩，郭军海，齐巍.基于经验小波变换的目标加速度估计算法［J］.北京航空航天大学学报，2015，41(1):154-159.Chen H，Guo J H，Qi W.Estimation of target’s acceleration based on empirical wavelet transform［J］.Journal of Beijing University of Aeronautics and Astronautics，2015，41(1):154-159(in Chinese).