综合孔径辐射计偏微分方程近场图像反演算法

姚现勋，尚晓舟，苗俊刚，李志平

(北京航空航天大学 电子信息工程学院，北京100191)

微波辐射计是一种微波无源遥感器，通过接收目标的微波辐射信号来获取目标的亮温信息，具有很好的安全性和隐蔽性，在反恐探测［1］、人体安检［2］等领域具有广泛的应用前景.相比于X-ray，微波成像系统不仅可以检测出隐藏在织物下的金属物品，还可以检测出陶瓷刀具、炸药等危险品，获得更加详尽、准确的信息.为了实时地获取高分辨率微波图像，综合孔径成像技术成为了人体安检领域的研究热点［3-4］.

综合孔径辐射计成像是将稀疏分布的小孔径天线之间的干涉测量通过数字波束合成的办法将其综合成一个大的等效孔径，并通过干涉测量获得的可视度函数反演得到视场范围内的亮温分布.理想情况下，在天线远场区，可视度函数与目标亮温分布之间满足傅里叶变换关系.然而，对于人体安检等领域的应用，探测目标处于天线阵的近场区域，此时可视度函数与目标的亮温分布不再满足傅里叶变换关系［5］.因此，近场成像方法成为了综合孔径辐射计应用于近距离探测领域的一个关键技术.文献［6］采用修正相位的点聚焦算法以重建相位修正后的可视度函数与目标亮温分布的傅里叶变换关系.然而，此算法对大视场范围的扩展目标无法进行准确的近场修正，成像误差较大.对于一维成像系统，文献［7］借助数值计算的方法，利用天线阵列形式及目标分布建立近场可视度函数矩阵，通过数值求逆的方式得到目标的亮温分布，消除近场误差.然而，对于二维成像系统，随着通道数目的增加，矩阵方程的稳定性急剧恶化，从而使得图像反演成为一种病态问题［8］.基于偏微分方程的正则化方法是求解病态问题的一种有效方法［9］.根据尺度空间理论，基于L2范数的各向同性扩散模型有利于去噪，但在保留图像边缘和细节方面存在不足;基于L1范数的各向异性扩散可以保持图像边缘细节，但会引入阶梯效应［10］.

本文将局部自适应偏微分方程的思想引入到综合孔径辐射计近场成像领域.利用目标分布的先验信息，将整个视场范围分为背景区域和目标区域.在图像背景区域利用L2范数进行噪声抑制，在目标区域利用自适应全变分模型来保留图像边缘.在滤除测量噪声的同时更好地保留图像边缘细节信息.为了验证该反演算法的有效性，采用一套48通道的二维综合孔径辐射计BHU-2DU进行了仿真、实验验证.结果表明，此算法比传统的偏微分方程方法更有效地减小了可视度测量噪声对亮温图像反演的影响.

1 综合孔径辐射近场成像模型

干涉式综合孔径辐射计测量的是不同天线单元接收信号的复相关值，即可视度函数.二元干涉仪是构成综合孔径辐射计的基本单元，其干涉测量的几何关系如图1所示.天线阵列位于z=0平面上，辐射面源位于z=h平面上.

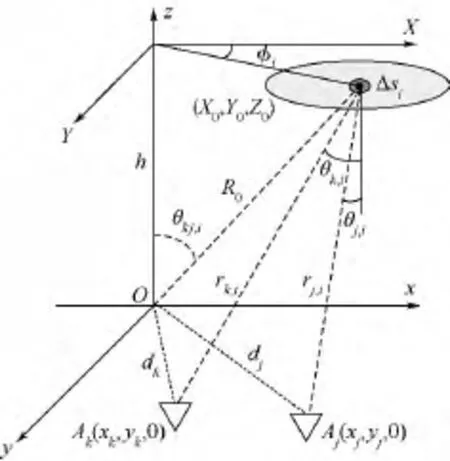
图1 近场干涉测量几何关系图Fig.1 Near field geometric diagram of interferometry

将面辐射源离散成P个小面源.理想情况下，对任意两天线单元的接收信号进行复相关运算，测得目标的可视度函数为［5］

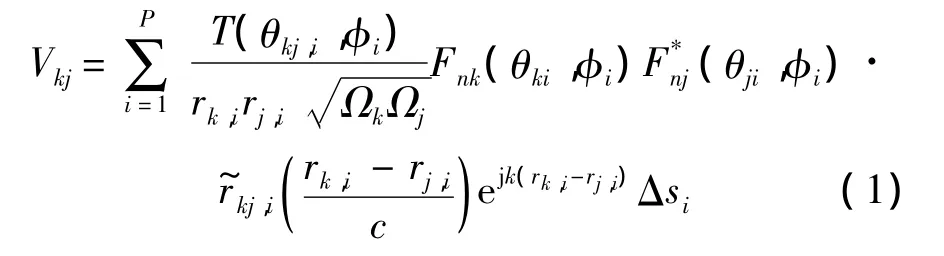
其中，T(θkj，i，φi)为第i个小面源的辐射亮温;rk，i和rj，i分别为该小面源到两接收天线之间的距离;Ω为单元天线的固体角;Fn为归一化的天线电压方向图;为考虑了空间去相关效应的条纹洗涤函数;对于理想窄带系统，去相关效应≈1，可以忽略.综合孔径辐射计的远场条件通常定义［11］:

其中，D为天线阵的孔径尺寸;λ为系统工作频率所对应的波长.此时，式(1)描述的可视度函数变为目标修正亮温的傅里叶变换，直接对测得的可视度函数进行逆傅里叶变换就可获得目标的亮温分布.对于近场情况，测量的可视度函数不仅与天线阵列的分布有关，且与目标场景的空间位置有关.因此，综合孔径近场成像的复杂性使得其不存在精确的解析解.考虑到实际系统中只能测得可视度函数离散采样点的值，式(1)可转化成离散矩阵方程的形式:

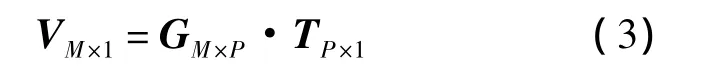
其中，G为系统响应矩阵;M为可视度函数采样点个数.理想情况下，可直接通过矩阵求逆获得精确的近场亮温图像.然而，为了保证足够的离散精度，通常情况下有P≥3M［8］.因此，此方程组为欠定方程组，解不唯一.同时考虑到实际系统不可避免的测量噪声，其近场可视度模型式(2)转化为

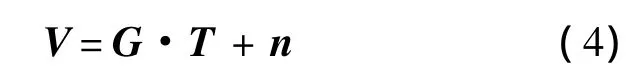
其中n为可视度采样测量噪声.上述矩阵方程的稳定性主要是由系统响应G矩阵的条件数决定，并随着去相关效应的加剧、接收通道数目的增加而增大.实际中为了达到所需的视场范围和空间分辨率，成像系统通常需要较多的接收通道，从而使得综合孔径辐射计近场图像反演成为一个病态求逆问题，即微小的测量噪声也可能导致反演图像的完全失真.正则化是将病态问题良性化的一个有效方法，其基本思想是利用解的先验知识，构造附加约束或者改变求解策略，使得逆问题的解变得稳定和确定.

2 基于偏微分方程的成像算法

2.1 偏微分方程正则化方法

图像反演中，正则化方法是通过极小化下面的约束误差方程来求得目标的亮温分布［9］:

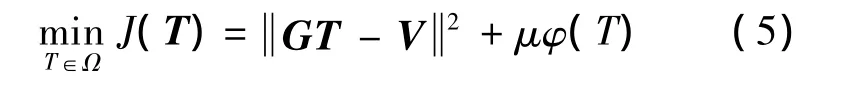
其中，第1项表示估计值与实际数据的误差;第2项为解的边界约束;Ω为图像的支持域;μ＞0为正则化参数.对于基于L2范数的偏微方程成像模型，边界约束为

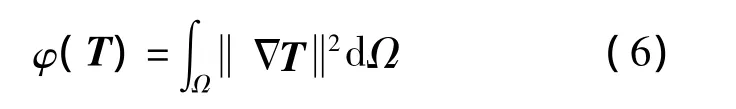
代入式(5)，可得其Euler-Lagrange方程为

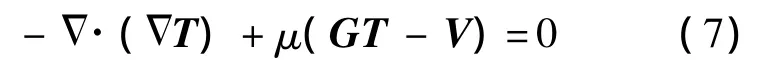
从上式可看出，扩散项 ·(T)的扩散系数为1，即在各个方向上具有相同的扩散能力.因此，该方法能够滤除噪声，但会损失图像的细节和边缘信息.

为了保持图像边缘，基于L1范数的全变分模型将式(5)中的边界约束改写为［10］

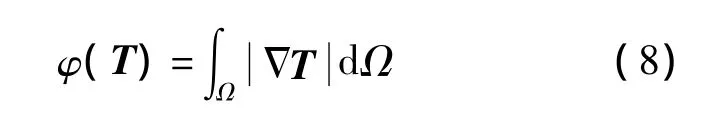
其对应的Euler-Lagrange方程为

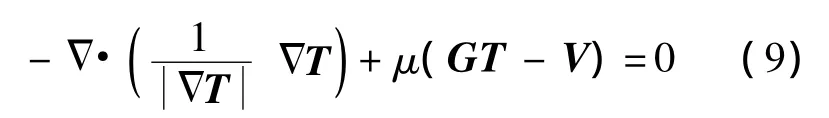
2.2 局部自适应偏微分方程方法

为了实现较高的空间分辨率，需要较大的综合孔径尺寸，在这种情况下，为了减少接收机通道数量降低运算复杂度，系统的天线间隔需要增加.然而，较大的天线间隔将造成完全混叠的视场范围，因此，需要采用背景对消［11-12］的办法获得一定的视场范围.虽然这种方法不能获得目标的绝对亮温，但是，在安检等应用中，相对亮温图像已经能够满足应用需求.在背景对消情况下，系统获得的差分可视度可表示为

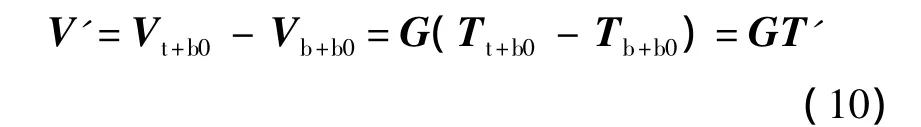
其中，Vt+b0表示目标场景Tt+b0的可视度函数;Vb+b0表示背景场景Tb+b0的可视度函数;下标t表示视场范围中存在目标时的目标区域;下标b表示视场范围中不存在目标时的目标区域;下标b0表示视场范围中除目标区域外的背景区域;T'表示待求解的差分亮温图像，为目标亮温与背景亮温之差.

经背景对消处理后，待求解的差分亮温图像一般可以分为两个特征区域:背景区和目标区，且具有明显的分界线.根据此先验信息，提出一种局部自适应偏微分方程的综合孔径辐射计近场成像方法，在不同的图像区域采用不同的约束，其模型为

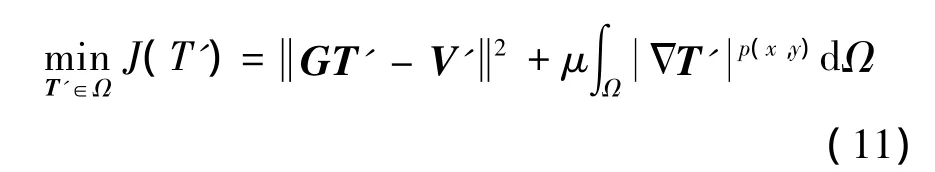
其中

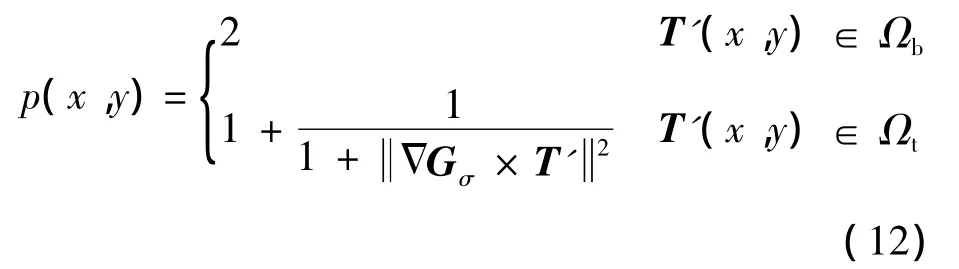
其中，Ωb为图像的背景区域;Ωt为图像的目标区域;Gσ为高斯滤波器，用来对噪声图像进行预处理.式(11)对应的Euler-Lagrange方程为

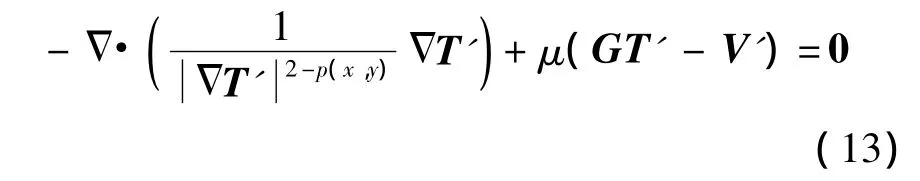
上式表明，该模型在图像背景区域采用基于L2范数的偏微分方程模型，以便尽可能地抑制噪声;在目标区域采用自适应全变分模型，边缘处较大，p≈1保持图像边缘;平坦区较小，p≈2抑制噪声.根据目标区域的图像特征自适应的选择扩散方向，从而在保持边缘的同时有效地抑制了阶梯效应.实际中，首先采用点聚焦FFT［6］获得质量较差的场景亮温图像，从中提取出目标的轮廓，再采用本文的方法对目标图像进行精确反演.对方程(13)，可采用两步迭代方法(TwIST)进行快速求解［13］.

3 近场成像仿真

为了分析上述图像反演算法的正确性及可行性，根据现有系统BHU-2D-U的技术参数进行了成像仿真，其主要参数如表1所示.

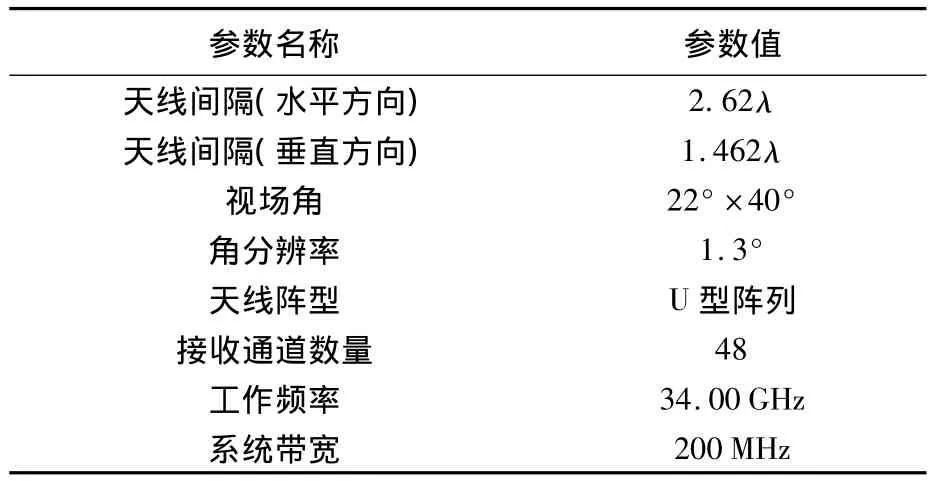
表1 BHU-2D-U系统主要参数Table1 Main specifications of BHU-2D-U

根据上述参数，为满足远场成像条件，BHU-2D-U的天线阵与探测目标的距离需大于39.1m.然而，为了获得1 m×2 m的视场范围，其成像距离限制约为3 m，属于近场区域，无法直接采用傅里叶变换进行成像.仿真的原始场景如图2(a)所示，人体亮温设为280 K，周围环境设为0 K，人体所携带的金属枪亮温设为150K，人体腿部携带的刀具亮温设为210 K.考虑到实际系统中，由于有限积分时间引入的可视度测量噪声.当接收机的频率响应近似为矩形时，测量噪声的方差可近似为［14］其中，B为系统带宽;τ为有效的积分时间;TA为天线温度;TR为接收机等效温度;Λ(x)为三角函数.系统为单边带结构，因此Λ(2Δf/B)=0.忽略接收机不理想性，当积分时间为0.5 s时，可视度函数的信噪比约为33.4 dB，分别采用L2范数、全变分及本文所述方法应进行图像反演.仿真结果分别如图2(b)、图2(c)、图2(d)所示.

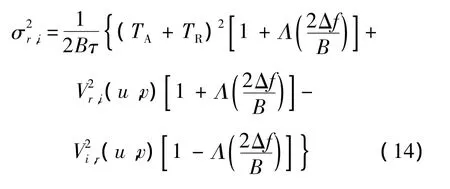
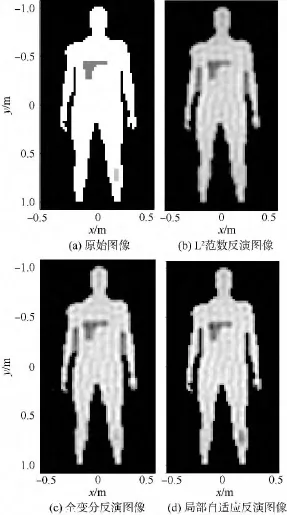
图2 不同反演算法的仿真结果Fig.2 Simulation results of different reconstruction algorithms

对比结果可以看出，由于测量噪声的影响，采用L2范数反演图像(图2(b))的噪声抑制并不充分，且人体携带的刀具几乎无法识别.这是因为该算法在整幅图像都采用同一种约束，很难在保持整幅图像边缘细节和抑制噪声之间折衷.全变分方法虽然在保持图像边缘细节的同时具有一定的去噪能力，但由于噪声抑制不充分，在目标区域及周围背景区域产生了阶梯效应.局部自适应的方法将待反演图像分区，克服了整幅图像都采用同一种约束的缺点，使得其反演获得的图像具有更低的背景噪声及更突出的边缘信息，同时有效地抑制了阶梯效应.上述反演图像中的波纹振荡是由于有限孔径截取造成的Gibbs效应，可以通过加窗的方式进行改善，但会降低空间分辨率.为了更加客观地描述不同反演算法的性能，采用反演图像与理想图像的均方根误差(TRMSE)来衡量反演图像的质量:

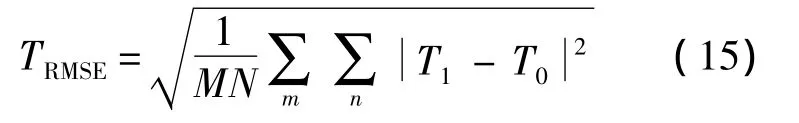
其中，T0为理想图像;T1为反演图像.利用上式，分别计算出采用L2范数、全变分及局部自适应方法获得的亮温图像的 TRMSE分别为 10.139 9，9.3593和7.2055.因此，采用本文提出的局部自适应方法获得的亮温图像的质量均优于其他成像算法.仿真中，不同算法的迭代停止准则均设置为前后两次迭代图像的均方根误差小于0.1.为了验证不同测量噪声水平情况下该反演算法的性能，分别选取积分时间 t为0.1，1，10 s时进行仿真，反演结果的相对均方误差如表2所示.

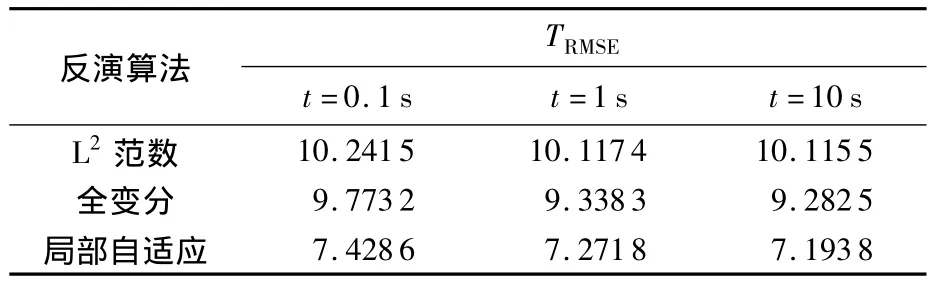
表2 不同反演算法的均方根误差TRMSETable2 TRMSEof different reconstruction algorithms

由表2可以看出，不同测量噪声水平下，局部自适应算法均具有较好的适用性，一定程度上减小了可视度测量噪声对亮温图像的影响.仿真中，正则化参数μ需根据不同可视度测量噪声水平进行调整.另一方面，由于实际中无法准确获知目标与天线阵的距离信息，只能进行近似估计.下面对存在距离误差的情况下进行仿真，成像距离设为3 m，估计误差范围为3±1 m.同样，在积分时间为0.5 s时仿真结果如图3所示.

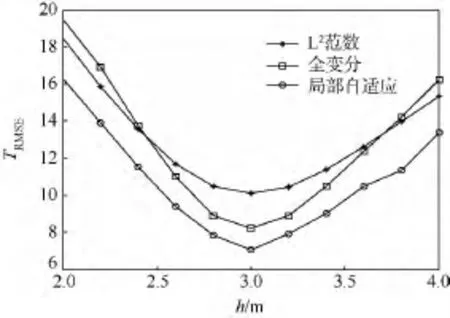
图3 存在距离误差时各反演算法的均方根误差TRMSEFig.3 TRMSEof different reconstruction algorithms caused by imaging distance error

从图3可以看出，随着成像距离误差增大，图像反演误差逐渐增加，且前向距离误差比后向距离误差的影响更大.对比不同反演算法的结果可知，当存在有距离误差时，采用局部自适应算法的反演结果的相对均方误差均小于其他两种算法.同时表明，局部自适应算法对成像距离误差具有更好的适应性.上述仿真的实验平台为一台CPU型号为3.30GHz Intel(R)Core(TM)i3-2120、内存为8 GB的计算机，仿真软件为Matlab 2013.在此平台上，该算法的平均运行时间约为1.6 s.

4 实验验证

为了进一步验证本文提出的近场图像反演算法的有效性，利用现有的一套8mm波段二维综合孔径辐射计系统BHU-2D-U(如图4所示)，对人体进行近距离的成像实验.在进行图像反演之前，需先测得BHU-2D-U的系统响应G矩阵.本实验中，利用一个安装在机械扫描架上的外部单点源逐点扫描的方式获得系统响应G矩阵［15-16］，此处系统视场范围与G矩阵测量范围一致.然而，由于机械扫描架尺寸的限制，本实验中BHU-2D-U的视场范围被限制为70 cm×70 cm.

图4 被动毫米波成像系统BHU-2D-UFig.4 Passive millimeter-wave imaging system of BHU-2D-U

实验场景如图5(a)所示，被测人员位于BHU-2D-U系统正前方约2 m处，右手在胸前持有一个V型的金属架.为了形成一个均匀的冷背景，在人体背后放置了一块与地面大约成45°夹角的铝板，用来反射天空亮温.实验中，积分时间设置为0.5 s.图5(b)给出了采用本文提出的局部自适应方法获得的近场毫米波图像.实验中，首先利用近场点聚焦FFT算法获得模糊的亮温图像，以划分待反演亮温图像的背景区域与目标区域.可以看出，虽然在光学图像中金属架的一部分被隐藏在衣服下面，但在毫米波图像中可以清晰地识别出该金属架的轮廓.为了对比不同成像方法的性能，分别采用L2范数、全变分方法进行毫米波亮温图像反演，其结果分别如图5(c)、图5(d)所示.实验中，考虑到实际系统误差的存在，将算法的迭代停止准则均设置为前后两次迭代图像的均方根误差小于0.3.

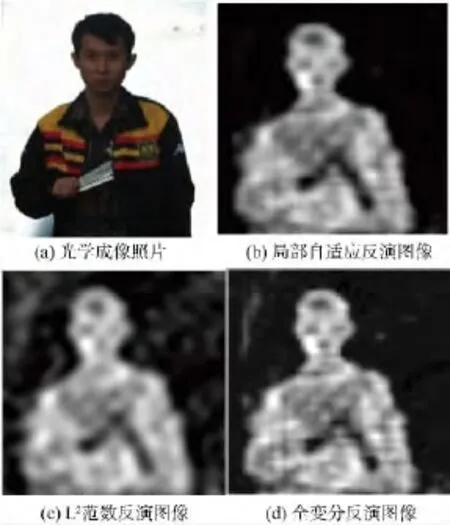
图5 不同反演算法的实验结果Fig.5 Experimental results of different reconstruction algorithms

实验结果表明，采用L2范数的反演图像由于平滑特性导致图像分辨率较低，金属架的轮廓并不清晰.全变分法提高了分辨率，但由于较高的噪声引入的阶梯效应非常明显，金属架轮廓部分已出现不连续情况，影响对人体隐匿物品的识别.局部自适应方法既去除了背景区域噪声又抑制了目标区域的阶梯效应，具有较好的图像反演效果.

5 结论

本文根据毫米波人体安检图像特点，提出了一种基于局部自适应偏微分方程的综合孔径辐射计近场图像反演算法.此算法根据待反演亮温图像的分布特性，对不同的区域采用不同的约束，以达到去除噪声且保持图像细节边缘的目的.对此算法进行了仿真和实验验证，结果表明:

1)该算法对近场综合孔径辐射计图像反演具有明显的降噪和保持边缘细节效果，为安检应用中进一步的违禁目标分割、识别提供良好基础.

2)该算法在不同噪声水平下均可将反演图像性能提升约20%，且对近场成像距离的误差具有较好的适应性，进一步增加了该算法的应用价值.

然而，为了实现实时快速成像的目的，在以后的工作中需要对本文算法的运算效率进行重点研究.

References)

［1］ Kolinko V G，Lin S，Shek A，et al.A passive millimeter-wave imaging system for concealed weapons and explosives detection［C］//Proceedings of SPIE-The International Society for Optical Engineering.Orlando:SPIE，2005，5781:85-92.

［2］ Wikner D A.Progress in millimeter-wave imaging［C］//Proceedings of SPIE-The International Society for Optical Engineering.Bellingham，WA:SPIE，2011，7936:1-9.

［3］ Nova E，Romeu J，Torres F，et al.Radiometric and spatial resolution constraints in millimeter-wave close-range passive screener systems［J］.IEEE Transactions on Geoscience and Remote Sensing，2013，51(4):2327-2336.

［4］ Zheng C，Yao X X，Miao J G，et al.Initial results of a passive millimeter-wave imager used for concealed weapon detection BHU-2D-U［J］.Process In Electromagnetics Research C，2013，43:151-163.

［5］ Peichel M，Suess H，Suess M.Microwave imaging of the brightness temperature distribution of extended areas in the near and far field using two-dimensional aperture synthesis with hight spatial resolution［J］.Radio Science，1998，33(3):781-801.

［6］ Tanner A B，Lambrigsten B H，Gaier T M，et al.Near field characterization of the GeoSTAR demonstrator［C］//IEEE Geoscience and Remote Sensing Symposium.Piscataway，NJ:IEEE，2006:2529-2532.

［7］ Zhang C，Wu J，Liu H，et al.Imaging algorithm for synthetic aperture interferometric radiometer in near field［J］.Science China Technological Sciences，2011，54(8):2224-2231.

［8］ Anterrieu E.A resolving matrix approach for synthetic aperture imaging raidometers［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42(8):1649-1656.

［9］ 邹谋炎.反卷积和信号复原［M］.北京:国防工业出版社，2001.Zou M Y.Deconvolution and signal reconvery［M］.Beijing:National Defence Industry Press，2001(in Chinese).

［10］ Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12(7):629-639.

［11］ Laursen B，Skou N.Synthetic aperture radiometry evaluated by a two-channel demonstration model［J］.IEEE Transactions on Geoscience and Remote Sensing，1998，36(3):822-832.

［12］ 胡岸勇，苗俊刚.一种扩大8 mm波段综合孔径辐射计成像视场的方法［J］.红外与毫米波学报，2013，32(1):50-55.Hu A Y，Miao J G.A method to enlarge the FOV for 8 mm band synthetic aperture radiometer［J］.International Journal of Infrared and Millimeter Waves，2013，32(1):50-55(in Chinese).

［13］ Bioucas-Dias J M，Figueiredo A T.A new TwIST:two-step iterative shrinkage/thresholding algorithms for image restoration［J］.IEEE Transactions on Image Processing，2007，16(12):2992-3004.

［14］ Ruf C S，Swift C T，Tanner A B，et al.Interferometric synthetic aperture microwave radiometry for the remote sensing of the earth［J］.IEEE Transactions on Geoscience and Remote Sensing，1988，26(5):597-611.

［15］ Tanner A B，Swift C T.Calibration of synthetic aperture radiometer［J］.IEEE Transactions on Geoscience and Remote Sensing，1988，31(1):257-267.

［16］ Yao X X，Zheng C，Zhang J，et al.Near field image reconstruction algorithm for passive millimeter-wave imager BHU-2D-U［J］.Process in Electromagnetics Research C，2013，45:57-72.