新型三轴离心机系统构型及数学建模

常乐，刘正华，温暖，吴森堂

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

现代军事、国防领域对某些无人高速飞行器的机动性能要求很高，即要求其具有很强的承受机动过载的能力［1-2］.国内外的实践证明，如果某些产品只做地面普通试验，不测试其承受高过载下的性能，可能会导致产品在机动飞行中失效［3］，为了在地面上验证无人高速飞行器的整体强度，就需要有一套可以模拟其在运动中承受载荷的设备［4］.查阅国内外相关文献，发现国内外至今缺乏对其的研究资料，固体火箭发动机高速旋转试验台［5］虽然实现了高速旋转条件下固体火箭发动机推力、压力的同时测量，但此试验台不能实现对飞行器进行离心过载的模拟试验.根据离心机系统可以通过高速旋转产生几十倍重力加速度的超重环境这一特性［6］，本文设计了一套小型无人高速飞行器载荷模拟系统，通过理论分析计算，实现模拟3个方向连续变化的动态过载，从而验证产品是否有较好的机动性能［7］.与常见的卧式螺旋离心机［8］和三足式离心机［9］不同，本文提出的离心机由1台底座和3个转动框架组成，这种结构形式在之前的国内外文献中研究很少.

1 过载模拟系统结构

过载模拟系统的机械结构如图1所示，由底座、地面导轨辅助支撑机构和3个转动框架组成.其中地面辅助支撑机构主要用来解决大转动惯量外框的配平问题［10］，同时增加整个离心机系统的刚度和强度;转动机构通过外框主轴的精确速度控制，形成综合的离心加速度，同时通过改变内框、中框两轴的角度转换得到负载需要的3个法向过载力.从图1可知，外框沿着主轴以角速率ω转动，内框可以绕附轴Ⅱ转动，设转动的角度为θ1，中框可以绕附轴Ⅰ转动，设转动的角度为θ2.考虑到机械结构，质量块放置时沿附轴I高出内框水平平面0.1 m，通过改变内框、中框两轴的角度和外框的转速，可以实时准确模拟出如图1所示的x，y，z 3个方向连续变化的动态过载.

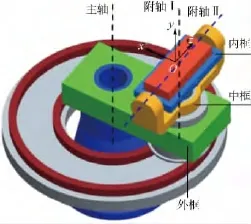
图1 过载模拟系统机械本体三维图Fig.1 Three-dimensional structure of overload simulation system

2 数学建模

2.1 过载的定义

设N为作用在对象上的除重力G以外的所有外力的合力，定义过载为n=N/G，方向与N一致［11］.

1)离心机过载.

定义离心机过载为外框高速旋转(角速度为ω，角加速度为dω/dt)时，在离心机质心处产生的过载(距离主轴回转中心距离为R).此处受到法向过载GN、切向过载GT分别为

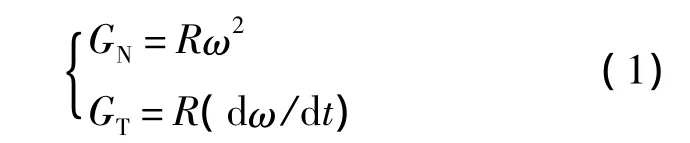
2)机动过载.

无人高速飞行器在飞行过程中承受的载荷，也是过载模拟系统需要模拟的过载.通过改变转角θ1，θ2以及外框转速ω可以改变伺服机构受到的过载大小以及方向.

2.2 坐标系的建立及绕旋转矩阵的定义

在研究初期，忽略控制机构对旋转平台产生耦合带来的影响，仅考虑x，y，z 3个方向上的过载.建立如图2所示的坐标系.3个坐标系的建立均以中框旋转轴线与内框旋转轴线的交点为公共原点建立.Ox1y1z1坐标系为内框坐标系，固连于内框.Oz1轴与内框轴线重合，质量块可在Oz1轴上滑动(±200 mm)，Oy1轴垂直于内框载台表面，Ox1轴按右手定则与其他两轴成90°关系.因质量块可以沿着z轴(即附轴Ⅱ)移动，设移动后的质心为OL.Ox2y2z2为中框坐标系，Oz2轴与 Oz1轴重合，Ox2垂直于中框所在铅垂平面，指向如图2所示，Oy2与其他两轴按右手定则成90°关系.Ox3y3z3为外框坐标系，Oy3与Oy2轴重合，Oz3轴垂直于中框轴线与外框轴线所在平面并与Oy3轴垂直，Ox3按右手定则与其他两轴成90°关系.各坐标系中坐标轴的正方向如图2所示.

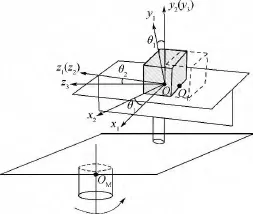
图2 过载模拟系统坐标系示意图Fig.2 Coordinate system schematic diagram of overload simulation system

按照以上方法建立坐标系后，质量块在载台上做指定运动时，其质心在内框坐标系的坐标表示为(0，0.1，z).下面介绍三框坐标系的变换关系.

设内框坐标系内的一点(x1，y1，z1)，其坐标变换到中框坐标系中，有

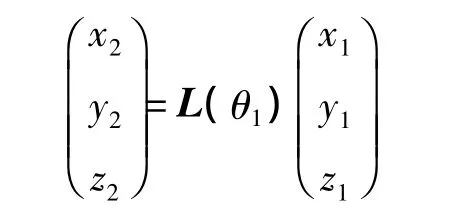
式中L(θ1)为旋转矩阵，且

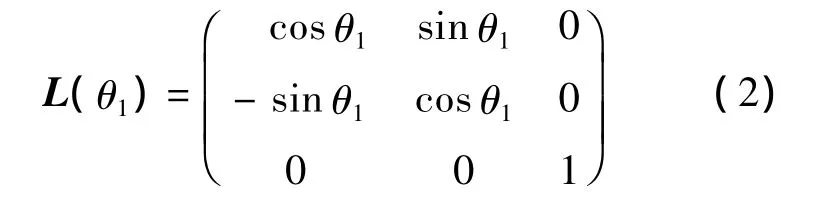
中框坐标系内的该点(x2，y2，z2)，其坐标变换到外框坐标系中，有

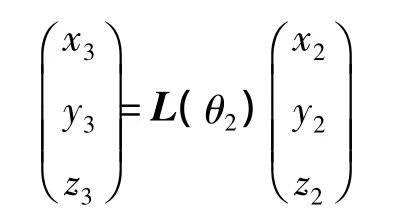
式中L(θ2)为旋转矩阵，且

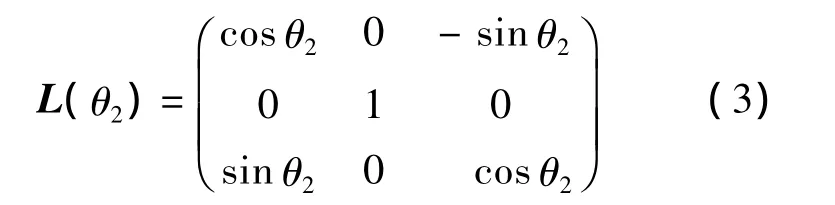
综合以上变换有

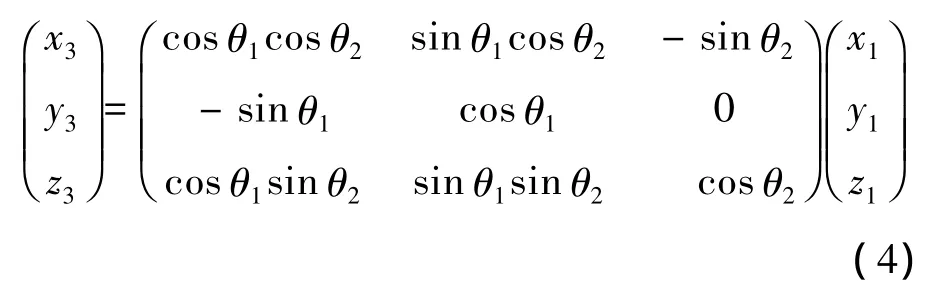
前面提到，当质量块在载台上滑动(±200 mm)时，其质心在内框坐标系的坐标表示为(0，0.1，z).则转换到外框坐标系内为

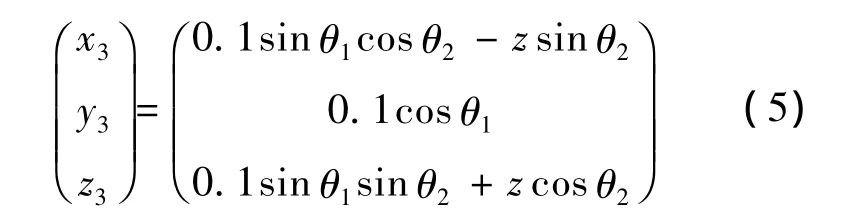
2.3 数学模型

当外框绕主轴旋转时，质量块有离心趋势，此时受到了可以按内框坐标系分解的3个方向的过载，假定力的正方向为坐标轴的正向，则变换到外框坐标系中:

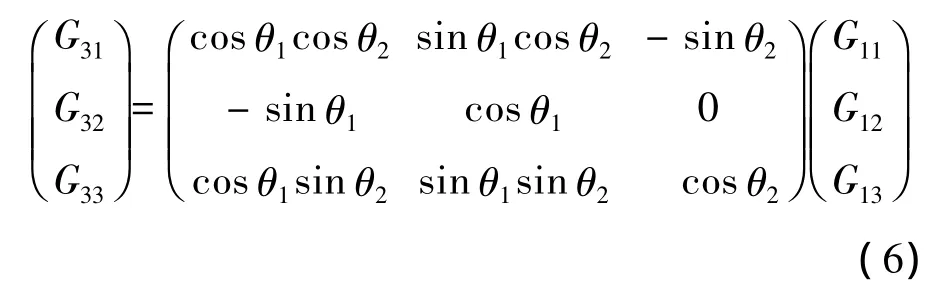
式中G的下标*1，*2，*3分别代表在各自坐标系内 x，y，z轴上的分量.

设外框旋转角速度为 ω，则在 x3，y3，z3轴方向上的过载［G31G32G33］为

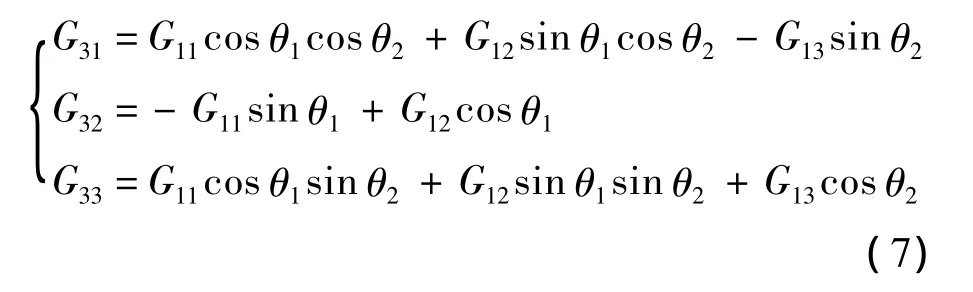
3 运动学分析

3.1 离心机以恒定的角速率ω做匀速转动

1)在x3轴方向上过载由向心力在该轴上的一个分量产生，即G31=rω2.其中r为质量块绕回转中心匀速转动的半径在x3轴上的投影长度.由于回转中心在外框坐标系内的坐标为(R，0，0)，而质量块坐标为

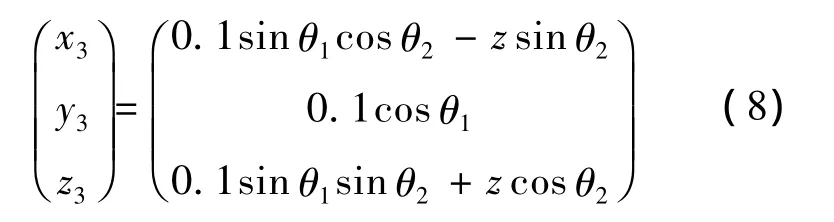
则由距离计算公式知:

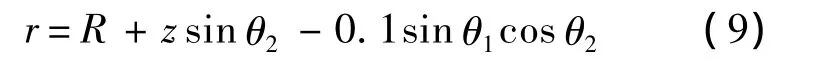
2)外框转动时，近似认为在y3轴方向上加载为0，即G32=0.

3)离心机做匀速转动，不产生切向加速度，但z3轴方向上的过载由向心力Gc在该轴上的一个分量产生，即 G33=Gcsin θ0，θ0为外框转角.其中，由加载的矢量合成，可得 Gc=对于 sinθ0的计算，有

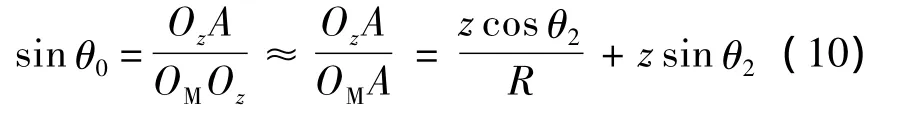
图3中，OM为外框回转中心，质量块在原点处质心为O，移动z后质心为Oz，构造直角三角形后，得 OzA=zcosθ2，OMA=R+zsinθ2.因为即使在z=±200 mm的情况下，OMA和OMOz依然是近似相等的，因而简化计算，可以用OMA代替OMOz，则得到3个坐标轴上的过载为

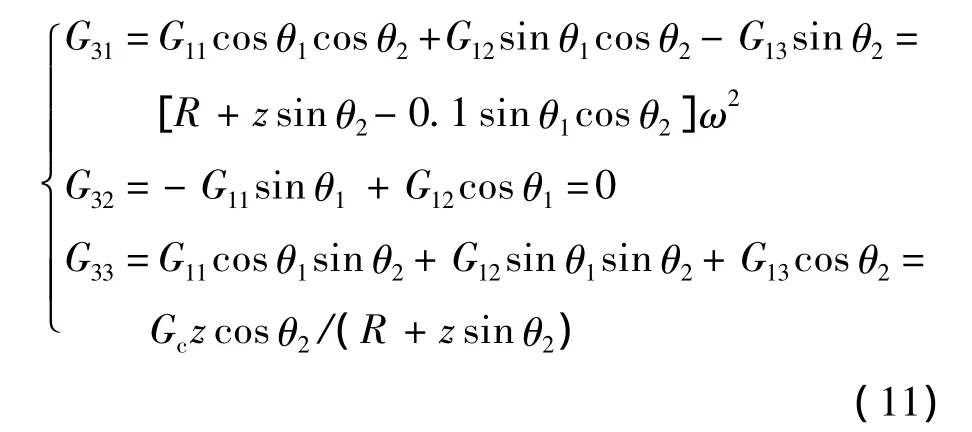
式中z为质量块沿z1轴上滑动的距离，延z轴正向为正.

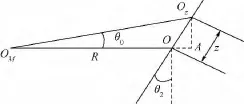
图3 转角计算图Fig.3 Calculating diagram of θ0

由上述方程组中的第2个式子解得

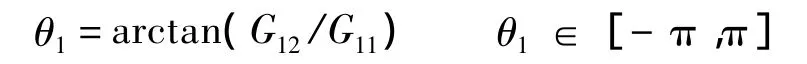
由式(10)第3个等式得

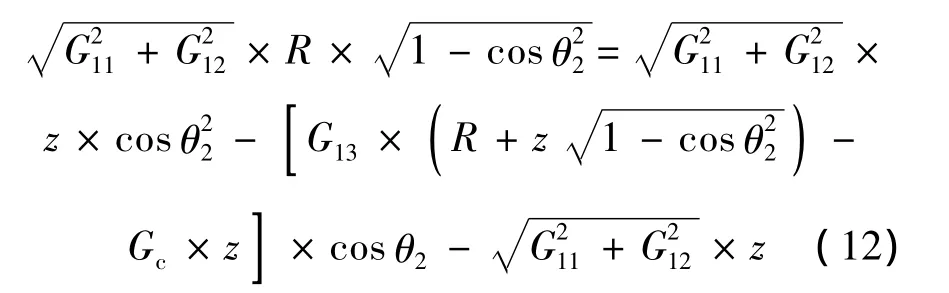
通过 Matlab 可以求出 θ2，θ2∈(－ π/2，π/2).求出了θ1和θ2，通过方程组第1个式子可以得出转速ω为

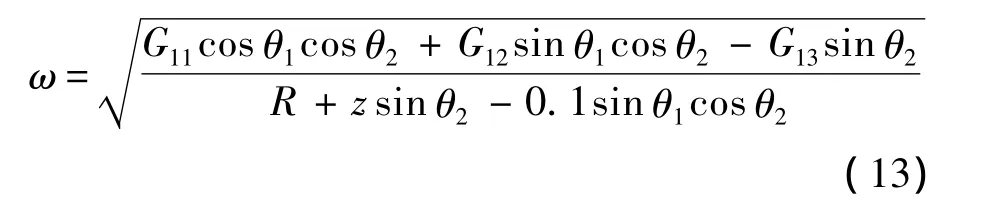
特殊情况:当z=0时，有

这样，如果已知内框加载块3个方向的过载［G11G12G13］，就可以求得 θ1，θ2和 ω.

3.2 离心机以加速度α做匀加速转动

离心机做匀加速转动，则z3轴上合力产生切向过载，即G33=rα，同样近似认为外框转动时在y3轴方向上加载为0，即 G32=0，在 x3轴方向上有法向过载 G31=rω2=r(αt)2.其中 r=R+z′+y′，z′为质量块沿 z1轴上滑动的距离在 x方向产生的距离，y′为质量块在y向上的100 mm偏心在x方向上产生的距离.

得到以下方程组:

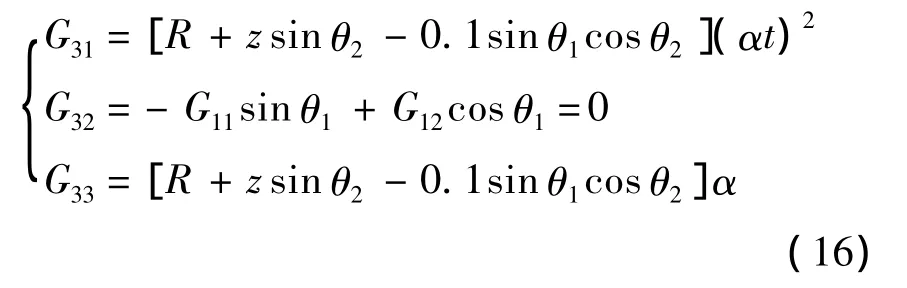
由上述方程组中的第2个式子解得

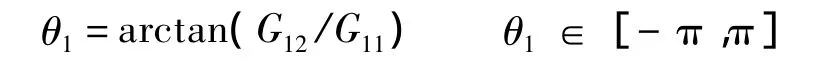
这种情况没有解析解，但可以算出切向过载G33对坐标系 OLx1y1z1下过载［G11G12G13］带来的影响［G1tG2tG3t］为

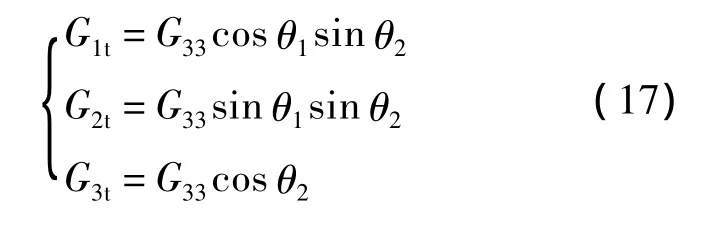
4 仿真验证

给定如图2所示x1，y1，z13个方向的过载大小和质量块在Oz1轴上的位移z，且给定质量块质量m=15 kg;距离主轴回转中心距离为R=0.8 m，重力加速度 g0=9.806 m/s2;依据以上解算方法，得到θ1，θ2和ω的仿真曲线及切向加速度对x1，y1，z13个方向加载产生的影响如下(见图4～图9):

1)过载大小恒定且为最大过载，即x1向过载为45g0;y1向过载为40g0;z1向过载为15g0.

2)x1，y1，z13方向的过载为如图7～图9所示的正弦曲线.

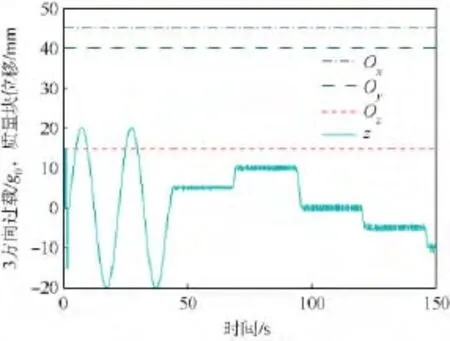
图4 恒定加载时3方向过载及质量块位移Fig.4 Overload in three directions and displacement of mass at constant loading

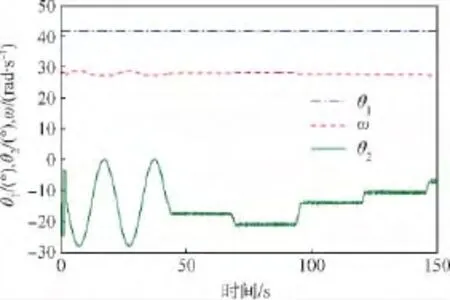
图5 恒定加载时模拟系统各变量曲线Fig.5 Variable curves of simulation system at constant loading

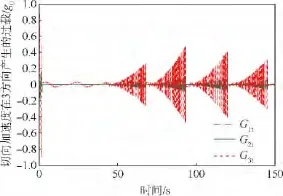
图6 恒定加载时切向加速度产生的误差曲线Fig.6 Error curves caused by tangential acceleration at constant loading

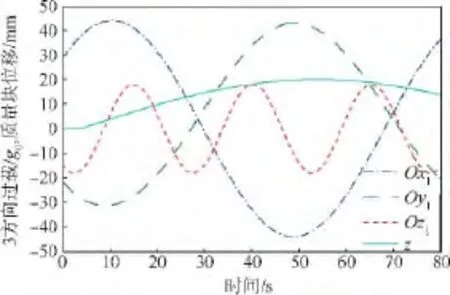
图7 加载变化时3方向过载及质量块位移Fig.7 Overload in three direction and displacement of mass at variational loading

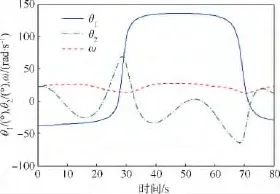
图8 加载变化时模拟系统各变量曲线Fig.8 Variable curves of simulation system at variational loading

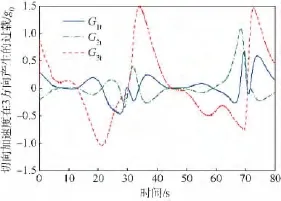
图9 加载变化时切向加速度产生的误差曲线Fig.9 Error curves caused by tangential acceleration at variational loading

5 结论

通过仿真曲线可以看出，该系统可以通过改变内框、中框的角度以及外框的转速，准确地模拟出各方向连续变化的动态过载，证明文中提出的过载模拟系统及反解算法是正确且有效可行的.

但是从仿真结果也可以看出反解出的过载和给定过载之间存在误差，产生误差的原因有:

1)进行过载模拟时，所需要的持续性过载由法向过载提供，但在离心机外框角速度改变时，会出现瞬时的切向过载，该切向加速度会对过载需求［G11G12G13］带来影响，但从图中可以看出误差在1.5g0之内.

2)文中提出的建模和解算方法是假设过载模拟系统是刚性体，并且轴系传动有很好的刚度，但过载模拟系统在实际运行时特别是在离心机高速转动时，结构上一定会产生形变［12］，这也会对最终结果带来影响.

3)从仿真结果可以看出，当给定的过载大小和频率变化较快，解算出的内框、中框的角度值和外框的转速变化也会复杂，这就对离心机的数字伺服控制系统提出了很高的要求，要求其能满足对内框、中框角度及外框转速的高动态、精确跟踪控制，控制中的滞后、非线性和外界未知干扰［13］也会对结果带来误差，因此必须通过设计先进的自适应控制器［14-15］使系统拥有很强的干扰抑制和稳定特性.

References)

［1］ 于进勇，顾文锦，张友安.导弹过载控制系统的非线性反演设计［J］.弹箭与制导学报，2004，4(S1):399-403.Yu J Y，Gu W J，Zhang Y A.Nonlinear backstepping design for missile overload control system［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2004，4(S1):399-403(in Chinese).

［2］ 梁雪超，杨军，邱峰.大攻角导弹法向过载控制的变结构设计［J］.计算机与现代化，2014，11(1):46-50.Liang X C，Yang J，Qiu F.Design of VSC for overload control in high angle-of-attack missile［J］.Computer and Modernization，2014，11(1):46-50(in Chinese).

［3］ 邓涛.空气炮加速度过载实验技术研究［D］.南京:南京理工大学，2011.Deng T.Research on the technology of acceleration overload tests by use of gas gun［D］.Nanjing:Nanjing University of Science and Technology，2011(in Chinese).

［4］ 戴邵武，张亦农.导弹过载控制设计方法研究［J］.弹箭与制导学报，2004，4(S7):97-99.Dai S W，Zhang Y N.Study on overload control for missile［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2004，4(S7):97-99(in Chinese).

［5］ 王彬，武晓松，余陵.固体火箭发动机高速旋转试验台设计［J］.南京理工大学学报，2005，29(5):536-539.Wang B，Wu X S，Yu L.Design of rocket engine test-bed with high-speed rotation［J］.Journal of Nanjing University of Science and Technology，2005，29(5):536-539(in Chinese).

［6］ 李果，黄孝斌.离心机控制系统设计［J］.系统工程与电子技术，2002，24(7):119-122.Li G，Huang X B.Design of the control system of the centrifuge［J］.Systems Engineering and Electronices，2002，24(7):119-122(in Chinese).

［7］ 袁冲，周洲.自主拦截无人机机动过载指标影响因素分析［J］.航空科学技术，2011(5):36-38.Yuan C，Zhou Z.Analysis of motor overload index influence factor about unmanned independently intercepting air vehicle［J］.Aeronautical Science ＆ Technology，2011(5):36-38(in Chinese).

［8］ 孙水平，李伟夫.卧螺离心机先进控制系统的应用［J］.纯碱工业，2013(5):31-33.Sun S P，Li W F.Application of horizontal screw centrifuge advanced control system［J］.Soda Industry，2013(5):31-33(in Chinese).

［9］ 徐罕.三足式离心机运行稳定性的监控［J］.科技与企业，2014(2):237-238.Xu H.The monitoring of running stability for the tripod type centrifuge［J］.Science and Enterprise，2014(2):237-238(in Chinese).

［10］ 杨亚非，霍鑫.离心机动不平衡量的配平方法［J］.中国惯性技术学报，2008，16(2):249-252.Yang Y F，Huo X.Balancing method of dynamic unbalance amount of centrifuge［J］.Journal of Chinese Inertial Technology，2008，16(2):249-252(in Chinese).

［11］ 陶笛.自寻的导弹捷联导引系统实现比例导引设计与研究［D］.哈尔滨:哈尔滨工程大学，2005.Tao D.Investigation on design of homing missile strapdown guidance system based on proportional navigation laws［D］.Harbin:Harbin Engineering University，2005(in Chinese).

［12］ 王昀绩.精密离心机动平衡系统控制方法研究［D］.哈尔滨:哈尔滨理工大学，2008.Wang Y J.Research on control of precision centrifuge dynamic balance system［D］.Harbin:Harbin University of Science and Technology，2008(in Chinese).

［13］ Ackermann J.Robust flight control:a design example［J］.Journal of Guidance Control and Dynamics，1981，4(6):597-605.

［14］ Hsu C F.Self-organizing adaptive fuzzy neural control for a class of nonlinear systems［J］.IEEE Transactions on Neural Network，2007，18(4):1232-1241.

［15］ Han H，Wu X L，Qiao J F.Nonlinear systems modeling based on self-organizing fuzzy-neural-network with adaptive computation algorithm［J］.IEEE Transactions on Cybernetics，2014，44(4):554-564.