基于AGENT的流感传播模型与分析——以香港流感模式为例

杨公立，赵继军

（青岛大学复杂性科学研究所，山东 青岛66071）

0 引言

流行性感冒简称流感，是由流感病毒引起的一种急性呼吸道传染病。流感病毒可分为甲（A）、乙（B）、丙（C）三型［1］，流感按照流行程度可分为世界大流行和季节性流行。流感新毒株在全球范围曾引起多次世界性大流行，包括西班牙流感 A（H1N1）、亚洲流感 A（H2N2）亚型和香港流感 A（H3N2）亚型等［2－4］。季节性 H1N1、季节性H3N2和新甲型H1N1等流感亚型每年则呈显著的季节性流行。流感的流行能导致严重的致病率和死亡率［5］，据世界卫生组织统计数据显示，流感每年在全球可导致5%－15%的人群感染，出现300万－500万严重病例，约有50万人死亡。此外感染流感后可使人更易感染其他传染病，如肺炎，因而增加了人类由传染病带来的风险［6］。

流感对人类的健康造成持续和无法预期的危害，因此一直是国内外公共卫生健康领域研究的热点。2009年的H1N1流感大流行以及2013年新发的H7N9禽流感（目前还没有证实在人与人之间传播），都曾对中国公共卫生健康造成了威胁，引起国家的高度重视。研究流感的流行病学特性，有助于流感预防和控制策略的制定。

流感有明显季节性规律，而且在温带和热带地区季节性流行规律有所区别。温带地区的冬季（12月－2月）属于发病高峰期，冬季高峰形成有多种解释理论，主要认为冬季的低湿度、低温度利于病毒的存活和增加病毒的传播力［7］；另外，冬季气温偏低，人在室内活动时间增加和人群之间接触更频繁进一步促使冬季流感高峰的形成。部分热带地区冬季也有流感流行的高峰，此外，每年的夏季（7月－9月）还有一个小峰值存在，因此有冬夏两季的双峰现象［8］。中国流感监测数据显示中国部分地处亚热带的省市也有冬夏两季的双峰现象［9］。目前，对流感夏季高峰的成因研究相对较少，并且一般是研究热带地区的降雨与该地区流感夏季监测数据波动的相关性［10］。然而根据动物实验结果，在温度高、相对湿度高（或仅在绝对湿度高）的情况下流感病毒通过飞沫的传播能力很低，甚至被完全抑制［7、11］，依此预测在亚热带或热带的夏季不会有因飞沫传播的流感流行高峰。夏季降雨（即高的绝对湿度）如何导致流感夏季的高峰这个问题一直没有很好的研究。

本文视流感传播为复杂系统，用复杂系统的建模方法对其进行建模与仿真。因为流感的流行传播作为一个动态系统包含了多层次（人、病毒、环境等），并且各层次个体间、不同层次的因素间存在相互作用与影响，这些特性是典型的复杂系统的特性。因此，有必要从复杂系统的角度研究流感传播的动态特性，以解释该系统的涌现（即流感流行的高峰）形成的根本原因。本文首先应用复杂系统建模方法中的基于主体的建模（agent－based modeling（ABM））建立流感传播的动态模型，对香港流感监测数据的动态特性进行计算机仿真，最后分析香港夏季流感流行高峰形成的原因。

1 研究方法与模型

本文采用基于主体的建模方法（ABM），把流感传播过程中各主体如人、病毒等建立在同一个流感传播的动态模型中。同时考虑人与环境之间的交互作用和流感传播的两种不同路径（空气传播路径、污染物传播路径）。

1.1 ABM

ABM已经在生态学、社会科学、政治、经济和分子生物学等领域广泛使用［12］。近几年，我国学者也将多主体建模应用在不同学科的研究中，如定量的建筑学问题［13］、高校保密项目管理系统的分析［14］等。自2001年ABM被应用在炭疽生物恐怖事件模型中，其在流行病学中的应用得到广泛关注［8］，典型的流行病ABM模型包括对假想的天花流行及控制措施效果的仿真［15］、对流感大流行的控制等［16］。这些流行病ABM着重于评估控制手段在根据人口数据建立的人群中的有效性，而忽略了主体与环境之间的交互。然而，对主体与环境间交互建模是ABM的优势。本文将利用这个优势，建立包括主体与环境交互的流感传播ABM模型。

ABM模型中，主体与主体以及主体与环境之间可以进行交互从而影响整个系统的动态。本文需要构建一个同时包括两种流感传播路径的流感传播模型，需充分的考虑人的异质性和环境因素之间的交互、环境中病毒数量及其受环境影响等因素，因此我们建立的流感传播ABM模型为多途径ABM模型，能够分析流感传播路径在不同季节的重要程度，有助于评估控制策略的有效性。

1.2 流感传播的ABM模型

应用Netlogo仿真平台建立流感的ABM模型。模型中创建了两类主体：人和病毒。主体人处于“易感”、“感染”、“康复”3种状态之一，所以分为易感者、感染者、康复者；病毒又分为存在空气中和存在污染物表面的病毒。主体人和病毒所处的空间环境表达为n个独立的空间栅格，本仿真模型由3 000个人和1 600个空间（40×40个栅格）组成，任意空间可用坐标（x，y）表示。主体人的数量和栅格数量的设定主要考虑了仿真时间和系统的随机性等因素。

现实中，流感病毒通过多途径传播，包括空气传播、接触传播（又分为直接接触如握手或与被病毒污染的物体表面接触，本文忽略通过握手的直接接触传播）。感染者通过咳嗽、打喷嚏等向环境中排放流感病毒，病毒悬浮在空中或逐渐落在物体表面。当易感者在有病毒的环境时，空气中的病毒随人的呼吸进入呼吸道并感染易感者，这种传播途径被称为空气传播途径；易感者在触摸有流感病毒的物体表面后再触摸眼、嘴、鼻，病毒因此进入人体内而感染易感者，这种传播途径被称为接触传播途径。进入易感者体内的病毒是否感染易感者，取决于从传播途径所摄入病毒的数量及相应的传染率，而且从不同传播途径摄入的病毒的传染率受气候因素的影响又有很大不同。

模型中建立两个传播途径，包括空气传播和接触传播。两种传播途径的建立是通过记录病毒分别在空气和污物上的数量，然后计算它们相应的传染率，从而确定是否感染易感者来实现。

本文的流感传播ABM模型对现实中复杂的传播过程进行了大量简化，主要研究不同传播途径在不同的季节对传播所起的作用。本文对模型做以下假设：

1）整个仿真过程不涉及人的自然出生和死亡，仿真过程总人数不变。

2）由于年龄、死亡率对流感动态的模式没有影响，所以模型不考虑这两个因素。

3）排出的病毒，如果包含病毒的液滴直径小于10μm，则假设液滴悬浮在空气中，这部分病毒的数量约占总病毒量的0.01%；如果包含病毒的液滴直径大于10μm，则假设液滴立即落在物体表面，忽略液滴在空气中下降到污染物表面过程［8］。

4）感染者排出的流感病毒只在感染者当时所处的空间内扩散，不扩散至邻近空间。

5）单位时间内，感染者向空间中排出病毒数相同。

6）在感染过程中，忽略人被感染的潜伏期。

初始化时，系统产生N（N＝3 000）个主体人并将它们随机分布在空间的栅格里。设定其中10个主体人的状态为感染者，800个人为康复者，其它主体人的状态均为易感者。初始化时还为任意主体人i（i∈N）设定感染时间TIi、免疫时间TRi、感染时刻tIi、恢复时刻tRi。感染时间TIi为从感染到恢复的时间长度，TIi服从正态分布N（D，σ2D），在［D－3σD，D＋3σD］范围内的值；其中D为平均感染时间，σ2D为感染时间变量的方差。免疫时间TRi为从获得免疫力到免疫力消失变为易感者的时间长度，TRi设定与TIi类似，限定在［R－3σR，R＋3σR］范围内；其中R为平均免疫力时间，σ2R为免疫力时间变量的方差。所设定的TIi、TRi值在以后的仿真过程中不再变化。本文仿真模型中设置感染时间TIi～N（7，1）且限定在［4，10］范围（单位为天）；假设TRi～N（360，32），且限定在［350，370］（单位为天）。平均感染时间和平均免疫时间的选取参考了文献［17］。感染时刻tIi为易感者变为感染者的时刻，恢复时刻tRi为感染者变为康复者的时刻。初始化时易感者和感染者的感染时刻tIi和恢复时刻tRi都设为0，康复者的tRi设为［130，170］之间的值。对于任意环境空间，空气中病毒量VA（x，y，t＝0）及物体表面病毒量VF（x，y，t＝0）初始时刻也设为0。

仿真时间步长设为1天。在每一仿真时间t，按随机顺序更新主体人的状态及其他参数。对于感染者，如果其实际感染时间大于该主体人已设定的感染时间TIi，则该主体的状态转换为恢复者。同时记录恢复时刻，tRi＝t，并清零感染时刻即tIi＝0。对于恢复者如果其实际康复时间大于设定的康复时间TRi，则该主体的状态转换为易感者。当主体i处于易感状态。首先判断主体人i所处的空间中是否有病毒。如果空间中有病毒，则根据病毒处于空气中或污物上及病毒量确定主体i是否被感染。设通过空气中的病毒感染的感染概率为ρA（i），通过污物上的病毒感染的感染概率为ρF（i）。空气中病毒的感染剂量远远小于污物上病毒的感染剂量。ρA（i）及ρF（i）与病毒量之间的关系如下：

这种病毒数与感染概率之间的函数关系是在简化了吸入（或触摸）等过程并近似感染剂量与感染概率后得到的，参数的选取主要参考了文献［8］。当ρA（i）＝0，ρF（i）＞0，主体人通过污物传播途径感染，感染概率为ρF（i）。当ρA（i）＞0，ρF（i）＝0，主体人通过空气传播途径感染，感染概率为ρA（i）。当ρA（i）＞0，ρF（i）＞0，主体人通过哪个途径被传染取决于ρA（i）和ρF（i）的相对值，如果系统产生的随机数p小于ρA（i）／（ρA（i）＋ρF（i）），则主体人通过空气传播途径感染；反之，通过污物的传播途径感染。本文模型简化流感病毒在人体内的感染过程，仅考虑两种传播途径的竞争，不考虑它们的共同作用，这种简化方法与考虑环境的传染病动力学模型中的方法类似。

模型还需要考虑到气候的季节性因素。Shanman等［7］对Lowen的动物实验结果进行重新分析，认为绝对湿度（AH）比相对湿度（RH）和温度更能准确反映气候因素对流感流行动态的影响。因此，模型中我们仅考虑绝对湿度对流感传播能力的影响。在夏季期间，当绝对湿度（AH）大于20g／m3时病毒通过空气路径传播会被抑制［11］，所以通过空气传播途径的感染概率为

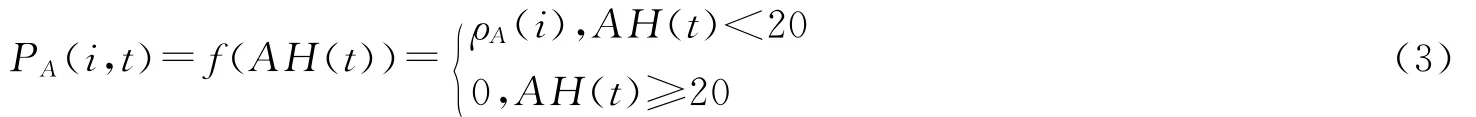
Lowen的动物实验结果还显示，流感病毒通过污物传播途径的传播能力不受绝对湿度的影响［7］，因此模型中假设流感病毒通过污物传播途径的传播能力不随气候的季节性发生变化。

每一仿真时间主体i会停留原处或移动到新的空间中。环境中的病毒量也是动态变化的。在每一仿真时间t，按随机顺序更新空间栅格中的病毒数VA（x ，y）及VF（x ，y）。如果空间（x，y）存在感染者，则每个感染者在单位时间t向空间（x，y）内空气中排出病毒量vA，向污物上排出病毒量vF。感染者在一定的环境中停留时间越长，向环境中排出的流感病毒数量越多。同时环境中的病毒量随着人的吸入或触摸物体表面而减少，在每一仿真时间t，空间（x，y）中状态为易感者或恢复者的主体人从空气中和污物上移除的病毒数分别为uA和uF。在环境中（空气中或污物上）的病毒不繁殖，有一定的死亡率，设空气中流感病毒死亡率为μA，污染物表面的病毒死亡率为μF。仿真时刻t结束时空间（x，y）的空气中和污物上病毒量分别为

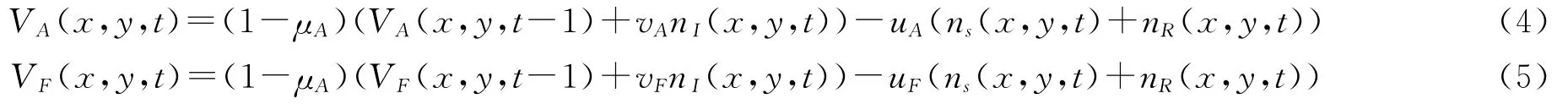
其中，VA（x，y，t－1），VA（x，y，t）分别为t－1，t时刻空间（x，y）空气中的病毒数，VF（x，y，t－1），VF（x，y，t）分别为t－1，t时刻空间（x，y）污染物上的病毒数，nS（x，y，t），nI（x，y，t），nR（x，y，t）分别为t时刻空间（x，y）中的易感者、感染者、康复者的人数。

在每个仿真时间步完成后都计算并更新易感者、感染者和恢复者的主体人数以及空气中病毒数总量和污物上的病毒总量。

2 以香港流感流行动态为例

2.1 香港流感流行动态

应用建立的流感传播ABM模型分析香港地区监测点流感样数据。首先，通过香港卫生署网站获得香港地区1998年到2012年的各监测点送检流感样品中流感病毒阳性数（Virus positive proportion（VPP））。本文用VPP%表示VPP在送检样品总数中占的的比例，由于流感样病毒大部分为H3N2，H1N1，所以只考虑这两种病毒亚型。文献研究表明可以通过VPP%研究流感传播动态［8］。1998—2012年之间的VPP数据中，除2001年和2005只存在一个峰值外，其他每年都存在明显的冬夏两个波动高峰，表明香港地区流感发病存在季节性双峰现象。图1为香港地区1998年—2012年流感样VPP数据百分比。图2为1998—2012年期间的每月VPP%平均值。流感样阳性峰值出现在2月和7月，其中夏季峰值比较低。

图1 香港地区定点监测流感样VPP百分比Fig.1 Hong Kong designated for the percentage of influenza－like VPP

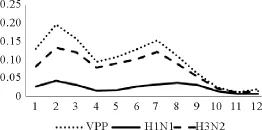
图2 流感样总VPP，H1N1（VPP），H3N2（VPP）的每月平均值Fig.2 The influenza－like total VPP，H1N1（VPP），H3N2（VPP）of the monthly average

香港在1—2月气温和绝对湿度最低，平均温度在15℃至18℃之间，绝对湿度在10g／m3至13g／m3之间，相对湿度68～73%。在6—8月气温、绝对湿度达到峰值，平均气温27℃～29℃，绝对湿度＞20g／m3，相对湿度＞80%［8］。

文献［11］中结果显示当空气中绝对湿度大于20（g／m3）时，病毒在空气中的传播能力消失。由于香港地区绝对湿度在5—9月时间超过20（g／m3），所以在模型中假设每年的第120—270天流感病毒不能通过飞沫传播，只可能通过污染物路径传播。式（3）更改为

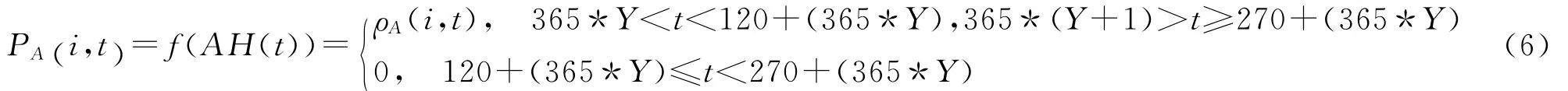
其中，Y 为仿真年，Y＝0，1，2，3，4，5，…。

2.2 仿真及结果分析

应用流感传播ABM模型对流感的动态进行仿真，并利用香港气候数据对公式（3）进行了修正。得到的发病人数随时间波动的曲线见图3。图3中的仿真输出均为一次仿真结果，且为显示清楚起见，仅显示了仿真输出中连续两年的结果。图3a为模型中夏季不包括污染物路径传播，图3b为夏季发生污染物路径传播。结果显示当模型中不包括污染物传播路径时，夏季不会形成流感波动高峰，只形成了一年一个峰值的波动；而当模型中包括污染物路径传播时，夏季有流感传播的小高峰。

图3 季节性因素影响流感感染人数仿真输出Fig.3 Seasonal factors affect influenza infections simulation output

为考虑系统随机因素对结果的影响程度，对所有的仿真实验重复100次并计算仿真结果的均值（100次仿真结果的标准差＜1.6）。结果显示通过空气传播途径感染的人数在冬季达到最高峰，最高峰值的平均值为ΕA＝385，远大于通过污物途径感染的人数在冬季的平均最高峰值ΕF1＝154。在整个冬季，通过空气传播途径感染的人数均大于通过污物途径感染的人数。因此，通过空气的传播途径在冬季流感的传播过程中起主导作用。污染物路径感染人数在夏季呈现第2次高峰，第2次高峰的平均值为ΕF2＝92。通过污物的传播途径在夏季流感的传播过程中起主导作用。

本文还检验了移动规则对仿真结果的影响。实验过程中的移动规则包括只移动1步（图4a）和随机移动［0，40］步（图4b）。仿真结果显示人的移动范围越小，流感波动峰值就越小。这相当于在现实世界人之间接触越频繁，活动范围越大会使流感波动峰值越高。

图4 不同移动规则情况下的仿真输出Fig.4 The simulation output of different rules of mobile case

3 结论与讨论

本文从一个新的角度来建立流感传播模型并解释亚热带地区香港流感传播的双峰现象。以往的流感传播动力学模型仅建立和分析一种传播路径的作用，而本文建立的流感传播ABM模型在一个系统中建立两种流感传播路径，同时加入了季节性对流感传播路径的影响。这种建模方法能够检验两种不同传播途径在不同季节对流感传播的相对重要程度。

流感的传播是一个复杂的系统，全面了解流感病毒、人、环境之间的关系需要多方面、多学科、多角度的分析流感传播。本文的模型简化了现实传播过程中的一些问题，如流感病毒通过握手传播等因素被忽略，也不考虑流感的潜伏期，并且主体人被赋予较简单的移动规则。但是流感的ABM模型重点研究了流感传播过程中的重要因素，并依此来分析流感发病动态规律产生的原因。

我们用所建的流感传播ABM模型分析了香港流感传播的动态特性产生的原因。在模型中，我们应用香港的绝对湿度数据对空气传播途径的传播能力进行了相应的校正。仿真结果涌现出流感的每年双峰现象，这与香港地区流感的冬夏双峰现象相匹配。结果分析显示，在绝对湿度的季节性变化的影响下，流感病毒的空气传播途径和污染物表面传播途径分别在冬季和夏季起主导作用。因此，香港流感传播的夏季峰值是由于病毒的污染物传播途径在夏季不受绝对湿度影响而仍然起作用而形成的。模型中病毒传播能力的假设符合动物实验的结论，同时仿真结果能够反映在夏季高绝对湿度的情况下流感的峰值仍然能够形成，而这看似矛盾的情况一直是在对热带、亚热带夏季峰值研究过程中困扰研究者的问题。

在流感的建模与分析过程中，通过空气的传播一直被认为是流感病毒的主要传播途径，而通过污染物的传播一直被忽略。本文的研究结果表明夏季流感峰值是由污染物传播路径形成，所以污染物传播也是重要的传播路径，在模型建立及相关的政策制定中应该得到充分的重视。

本文所建的流感传播ABM模型还可用于对其它地区如热带地区的多重流行模式（一部分地区没有峰值、部分地区有双峰、部分地区夏季单峰）驱动因素的分析。模型还可用于分析其他通过环境传播的病毒或细菌的传播动态，如分析MRSA在医院中是否可通过医护人员传播、MRSA在社区的传播等。

［1］ 王革非，李康生.新世纪流感大流行的思考［J］.生物化学与生物物理进展，2009，36（8）：945－949.Wang Gefei，Li Kangsheng.Origins and views of the 2009A／H1N1influenza pandemic［J］.Progress in Biochemistry and Biophysics，2009，36（8）：945－949.

［2］ Belshe R B.The origins of pandemic influenza－lessons from the 1918virus［J］.New England Journal of Medicine，2005，353（21）：2209－2211.

［3］ Kawaoka Y，Krauss S，Webster R G.Avian－to－human transmission of the PB1gene of influenza A viruses in the 1957and 1968pandemics［J］.Journal of Virology，1989，63（11）：4603－4608.

［4］ Mueller M.Influenza vaccine：a long way from Hong Kong［J］.Science，1968，162（854）：651.

［5］ Simosen L，Clarke M J，Schonberger L B，et a1.Pandemic versus epidemic influenza mortality，apattern of changing age distribution［J］.Infectious Disease，1998，178（1）：53－60.

［6］Shrestha S，Foxman B，Weinberger D M，et al.Identifying the interaction between influenza and pneumococcal pneumonia using incidence data［J］.Science Translational Medicine，2013，5（191）：191ra84.

［7］ Lowen A，Palese P.Transmission of influenza virus in temperate zones is predominantly by aerosol，in the tropics by contact［J］.Epidemiology，2009，8.

［8］Sheng L.Environmentally mediated transmission models for influenza and the relationships with meteorological indices［D］.The University of Michigan，2011.

［9］ Shu Y L，Fang L Q，de Vlas S J，et al.Dual seasonal patterns for influenza，China［J］.Emerging Infectious Diseases，2010，16（4）：725－726.

［10］Moura F E，Perdigao A C，Siqueira M M.Seasonality of influenza in the tropics：a distinct pattern in northeastern Brazil［J］.American Journal of Tropical Medicine and Hygiene，2009，81（1）：180－183.

［11］Shanman J，Kohn M.Absolute humidity modulates influenza survival，transmission，and seasonality［J］.PNAS，2009，106（9）：3243－3248.

［12］Railsback S F，Grimm V.Agent－Based and Individual－Based Modeling：a Practical Introduction［M］.New Jersey：Princeton University Press，2012.

［13］刘慧杰.多主体模拟的建筑学应用——以netlogo平台为例［J］.建筑设计研究，2009，27（8）：99－103.Liu Huijie.Plication of multi－agent simulation on architectural researches：taking netlogo platform as an example［J］.2009，27（8）：99－103.

［14］李艳，吴介军.基于 Netlogo的高校保密项目管理仿真分析［J］.计算机技术与发展，2010，21（4）：164－168.Li Yan，Wu Jiejun.Netlogo－based simulation and analysis of college confidential project management［J］.Computer Technology and Development，2010，21（4）：164－168.

［15］Epstein JM，Cummings D，Chakravarty S，et al.Toward a Containment Strategy for Smallpox Bioterror：an Individual－Based Computational Approach［M］.Washington D C：Brookings Institution Press，2004.

［16］Ira M.Longini，Jr.，et al.Containing pandemic influenza at the source［J］.Science，2005，309（5737）：1083.

［17］Dushoff J，Plotkin J B，Levin S A，et al.Dynamical resonance can account for seasonality of influenza epidemics［J］.PNAS，2004，101（48）：16915－16916.