具有干扰的多自主体系统的群集运动与速度同步

褚福芳，杨洪勇

（鲁东大学信息与电气工程学院，山东 烟台264025）

0 引言

群集运动问题一直受到物理、生物、工程等许多领域专家的广泛关注，所谓群集运动问题，即分布式系统中各个自主体之间按照一定的规则进行信息交换，使得自主群体渐近地取得相同的速度向量，两自主体之间的距离保持稳定并且没有碰撞发生。

基于图论和矩阵理论，许多控制学者在群集运动研究方面取得了显著成果。Olfati－Saber［1－2］提出了3个控制算法，第1个控制算法体现了Reynolds［3］的3条规则，第2个算法具有避免与障碍物相撞的功能，第3个算法中假设每个自主体都具有领航者的信息，对每个自主体增加引导反馈来实现目标跟踪的功能。苏厚胜［4－5］基于Godsil C［6］、Horn R A［7］提出的代数图论理论，研究了只有一部分自主体具有领航者信息的连通网络的情况，推广了原有的结论。俞辉和王永骥等人［8－11］研究了在固定／动态的网络拓扑中具有领航者的多智能体群集编队控制问题。当自主体模型参数存在不确定性或存在外界干扰时，群集运动问题变得更加复杂，更具有挑战性，我们针对一阶系统中存在的干扰，提出了采用干扰－观测器控制的移动智能体系统的一致性的算法［12］。刘佳等［13］研究了具有时变时滞动态拓扑和模型不确定性的多智能体，提出了多智能体系统的鲁棒H∞一致性算法。但是对于具有干扰的多自主体系统的群集运动研究，鲜有报道。

本文基于人工势能函数梯度结合干扰观测器控制方法，研究具有领航者的多自主体系统，通过引入干扰观测器对干扰进行观测，提出在干扰环境中取得群集运动和速度同步的分布式控制协议。

1 问题描述与预备知识

1.1 代数图论

定义无向图G＝ （V，E，A），其中V＝ ｛1，2，…，n｝ 是图G的节点集合，用来表示n个自主体，E⊆V×V，（vi，vj）表示图中边的集合，A＝ ［aij］是图G的权重矩阵，其中 ∀i∈V，aii＝0，aij＞0↔（vi，vj）∈E，aij＝0↔（vi，vj）∉E。结点vi的邻接集合为Ni＝ ｛j∈V，aij＞0｝ 。图G的Laplacian矩阵定义为

1.2 问题描述

基于无向网络拓扑图G＝（V，E，A），考虑n个自主体在2维欧式空间中运动，假设第i个自主体的动态方程描述如式（3）：

其中，qi＝（xi，yi）T是自主体i的位置向量，是自主体i的速度向量，ui＝（uxi，uyi）T是自主体i的控制输入向量，di为外界干扰，可以表示为如式（4）形式的外部动态子系统：

其中，wi为干扰内部状态，外部动态子系统（A，C）可观。

假设被控系统的状态向量均可用，则只需对干扰子系统进行观测，为了消除干扰di，引入的干扰观测器可以表示为如式（6）的表达式：

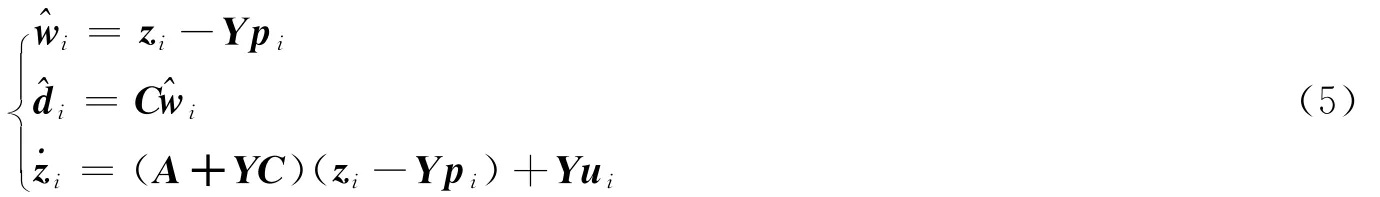
其中，zi为引入的辅助变量的估计，Y为待求矩阵。

定义1 如果自主群体（渐近地）取得相同的速度向量，自主体两两之间的距离保持稳定并且没有碰撞发生，就称自主群体（渐近地）取得了群集运动。

控制目标就是设计控制输入以使自主群体取得定义1意义下的群集运动与速度同步，为了解决这种问题，采用式（6）的分布式控制协议：

第1项ai用于自主体间的分离和聚合；第2项αi用于调整自主体i的速度，以使自主群体达到速度匹配；第3项βi为引导反馈项，用于实现与领航者的速度一致，分布式控制协议的具体表达式由方程（9）表示。假设领航者满足运动方程（7）：

qr＝是领航者r的位置、速度向量，本文主要讨论的领航者做匀速运动。

定义2 势场函数Uij是一个关于自主体i和自主体j之间相对距离‖qj－qi‖可微、非负、无界的函数，且满足：

1）当‖ｑj－ｑi‖ →０时，Ｕij（‖ｑj－ｑi‖）→ ∞；

2）Uij在某一合乎要求的距离处取得唯一的最小值。

取势场函数：

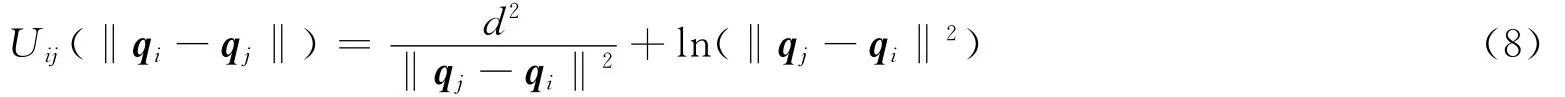
假设在网络拓扑G＝（V，E，A）中，自主体之间的通信或相互作用是时不变的，自主体i的控制输入ui取如式（9）的表达式：

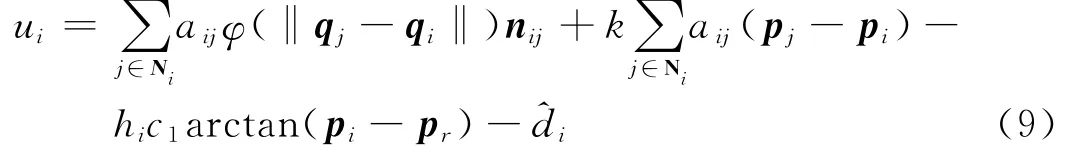
其中，k，c1为大于零的常量为单位向量；hi＝1，为自主体i能够获得领航者信息，hi＝0，表示不能获得领航者的信息；是对干扰di的估计。

图1 势场函数ψ（z）Fig.1 Potential functionψ（z）

2 主要结论

定理1 考虑存在领航者具有n个自主体的系统，由它们组成的网络拓扑为G＝（V，E，A），且G是无向连通图，每个自主体的动态方程为方程（3）所描述，控制输入由方程（9）表示，可以得到如下结论：

1）当系统中自主体没有受到外界干扰时，所有自主体的速度最终能够渐近收敛到领航者的速度，并达到群集运动。

2）当自主体受到外界干扰时，若存在正定矩阵矩阵P＞0，适当维数的矩阵Q使得矩阵不等式（10）成立

证明：1）讨论系统中所有的自主体都没有受到外界干扰时的情况，选取能量函数（11）：

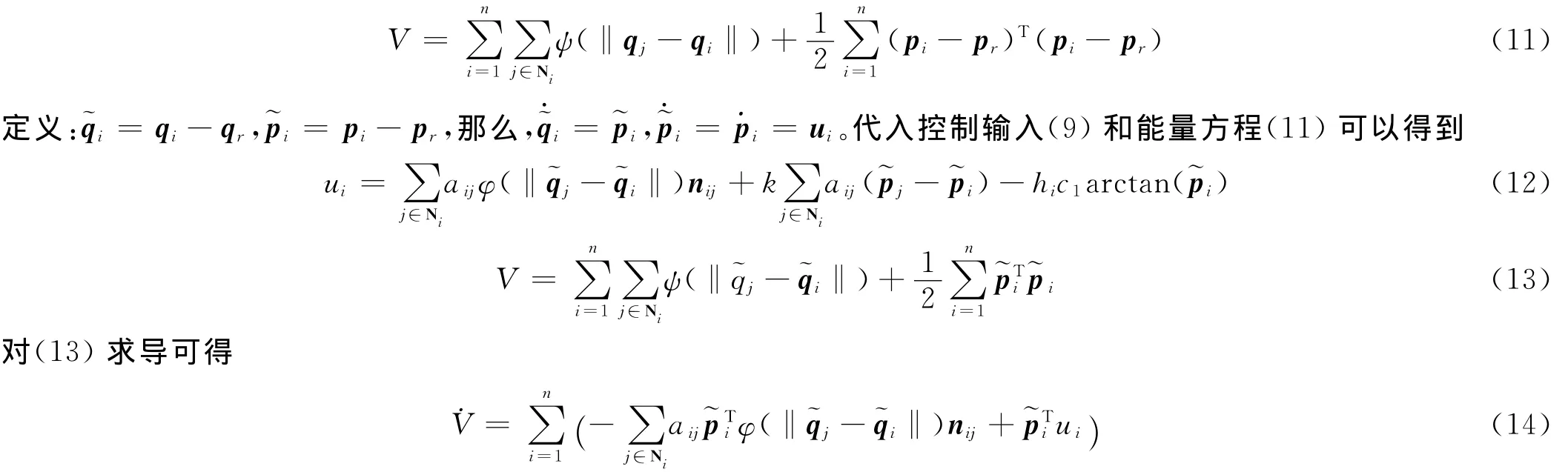
把方程（12）代入到方程（14）可以得到

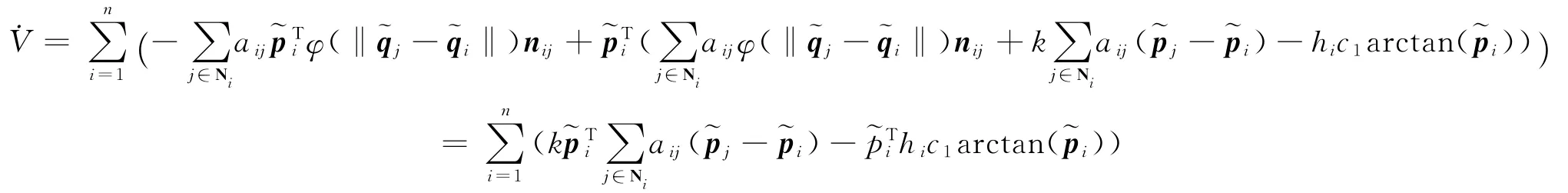
因为arctanx函数是类饱和函数，在原点附近可以做arctanx＝x近似，带入得

2）讨论系统中自主体受到外界干扰时的情况，定义误差变量e，则

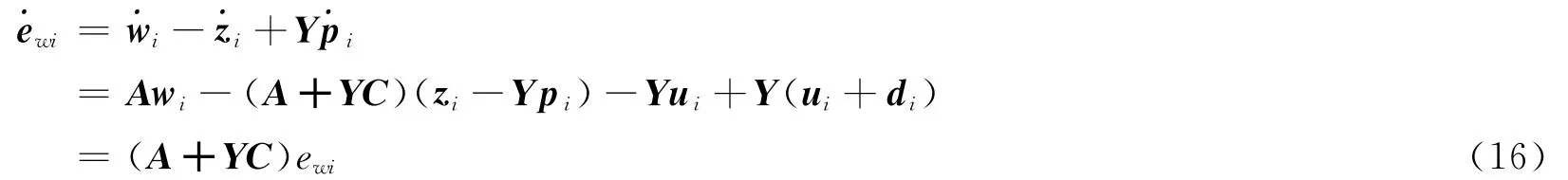
同样选取能量函数（18）

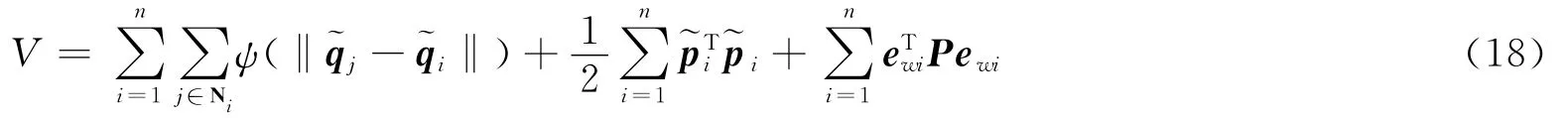
对式（18）求导可得

对arctanx函数做同样的近似处理，可以得到

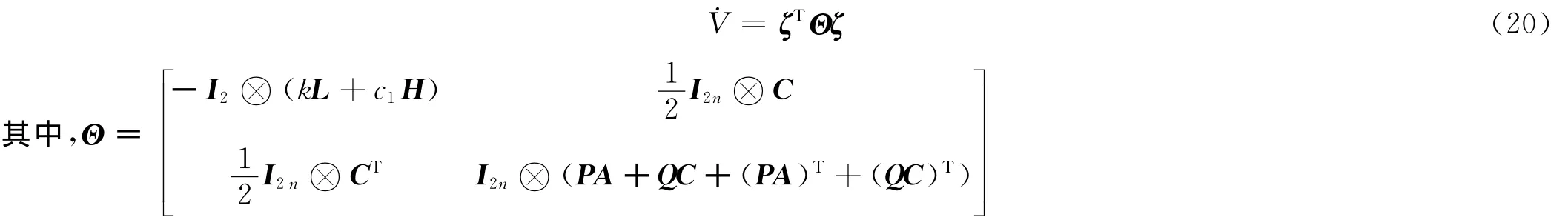
所以，由定理中的条件可以得到˙V＜0，则在干扰环境中也能取得群集运动与速度同步。

3 仿真结果

考虑由4个相同二阶运动模型的自主体组成的系统，其组成的网络拓扑如图2所示。势能函数为：Uij（‖qi－，其中d＝2，分布式控制协议的控制增益k＝1，反馈系数c1＝1。系统中各自主体、领航者的初始位置随机地在［0 10；0 10］的正方形区域内产生，自主体地初始速度的大小随机地在［0 1］范围内产生，方向任意，领航者的初始速度为：prx＝0.7，pry＝0.5。外界干扰子系统满足A＝干扰的初值为：wi（0）＝ ［0.25sin10.15cos1］ 。根据定理中的充分条件，求取的未知矩阵为

3.1 自主体没受到外界干扰时的仿真

假设4个自主体中，只有1号自主体能获得领航者信息，其余自主体与1号自主体组成的拓扑结构如图2所示，且是时不变的。4条曲线代表4个自主体的运动情况，点划线代表领航者的运动情况，图3、图4刻画的是领航者和自主体的速度随时间的变化情况，从图中可以看到，经过50s，4个自主体能够取得速度与领航者同步。图5刻画的是4个自主体、领航者在两坐标轴上的相对位置，经过足够的时间后，自主体与领航者的运动轨迹取得平行，即它们的速度趋于同步，从而形成编队。

图2 4个自主体互连拓扑结构Fig.2 Interconnected topology of 4agents

图3 自主体没有受到外界干扰时x轴的速度Fig.3 Agent′s xaxis velocities without disturbance

图4 自主体没有受到外界干扰时y轴的速度Fig.4 Agent′s yaxis velocities without disturbance

3.2 自主体受到外界干扰时的仿真

当自主体受到外界干扰时，自主体与领航者组成的拓扑结构与无干扰时的拓扑结构相同。图6、图7刻画的是自主体受到外界干扰时，没有引入干扰观测器时自主体、领航者的速度曲线。图8～10刻画的是自主体受到干扰时，通过设计基于干扰观测器的控制协议，自主体、领航者的运动情况。仿真结果表明，当自主体受到外界干扰时，自主体的速度在领航者速度上下震荡，引入干扰观测器后，自主体与领航者速度同步的调节时间变长，震荡次数增加，自主体的运动轨迹更加曲折。但是，经过70s后，所有自主体都同步于领航者的速度；自主体相对位置曲线最终都平行于领航者的相对位置曲线。

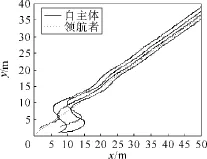
图5 自主体没有受到外界干扰时两坐标轴相对位置Fig.5 Agent′s relative position of two axes without disturbance

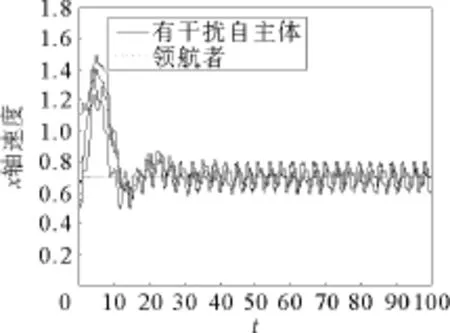
图6 自主体受到外界干扰时x轴的速度Fig.6 Agent′s xaxis velocities with disturbance

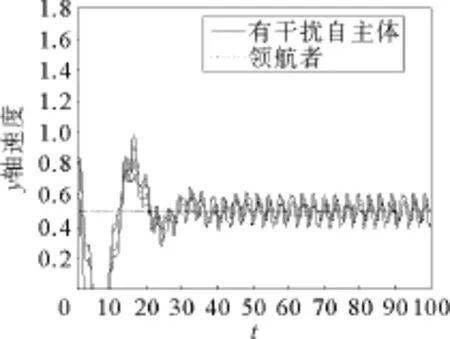
图7 自主体受到外界干扰时y轴的速度Fig.7 Agent′s yaxis velocities with disturbance

3.3 自主体受到外界干扰且领航者做变速运动时的仿真

当自主体受到外界干扰且领航者做变速运动时，自主体与领航者组成的拓扑结构与前面的拓扑结构相同。自主体和领航者的位置、速度初值的确定与前面确定方式相同，图11～13刻画的是引入干扰观测器后，设计基于干扰观测器的分布式控制协议且领航者做变速运动时的情况（领航者的加速度为：arx＝0.01，ary＝0.015）。由仿真结果来看，当自主体受到外界干扰且领航者做匀加速运动时，在调节阶段，自主体的运动轨迹与领航者的运动轨迹不同，经过足够的时间后自主体同步于领航者的速度，自主体与领航者的相对位置曲线取得平行，即取得了群集编队运动。

图8 引入干扰观测器后自主体x轴的速度Fig.8 Agent′s xaxis velocities when disturbance observer is imported

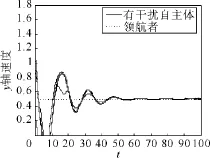
图9 引入干扰观测器后自主体y轴的速度Fig.9 Agent′s yaxis velocities when disturbance observer is imported

图10 引入干扰观测器后自主体两坐标轴相对位置Fig.10 Agent′s relative position of two axes when disturbance observer is imported

图11 引入干扰观测器且领航者做加速运动x轴速度Fig.11 Agent′s xaxis velocities when observer is imported and leader accelerated

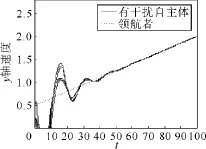
图12 引入干扰观测器且领航者做加速运动y轴速度Fig.12 Agent′s yaxis velocities when observer is imported and leader accelerated

图13 引入干扰观测器且领航者做加速运动两坐标轴相对位置Fig.13 Agent′s relative position when disturbance observer is imported and leader accelerated

4 结论

本文研究了基于无向连通网络的多自主体系统，通过引入干扰观测器对干扰子系统进行观测，提出了基于干扰观测器控制的分布式控制协议，此协议保证了自主体能够取得群集运动与速度同步，体现了控制协议对环境具有很强的适应性。本文的后续工作将对不同阶多自主体系统的群集运动进行研究。

［1］ Olfati－Saber R，Murray R M.Consensus problems in networks of agents with switching topology and time－delays［J］.IEEE Transactions on Automatic Control，2004，49（9）：1520－1533.

［2］ Olfati－Saber R.Flocking for multi－agent dynamic systems：algorithms and theory［J］.IEEE Transactions on Automatic Control，2006，51（3）：401－420.

［3］ Reynolds C W.Flocks，herds，and schools：a distributed behavioral model［J］.Computer Graphics，1987，21：25－34.

［4］Su Housheng，Wang Xiaofan.Pinning control for stable flocking of mobile agent［C］∥The Regional Inter－University Postgraduate Electrical and Electronic Engineering Conference.Macau，China，2006.

［5］ Su H S，Wang X F，Lin Z L.Flocking of multi－agents with a virtual leader［J］.IEEE Transactions on Automatic Control，2009，52（8）：1497－1475.

［6］ Godsil C，Royle G.Algebraic Graph Theory，Graduate Texts in Mathematics［M］.New York：Springer－Verlag，2001：265－295.

［7］ Horn R A，Johnson C R.Matrix Analysis［M］.Cambridge，UK：Cambridge University Press，2012：387－547.

［8］ 俞辉，王永骥，程磊.基于有向网络的智能群体群集运动控制 ［J］.控制理论与应用，2007，24（l）：80－83.Yu Hui，Wang Yongji，Cheng Lei.Flocking motion control of flock in directed networks［J］.Control Theory and Application，2007，24（1）：80－83.

［9］ 俞辉，王勇骥，程磊.稳定的有领航者的多移动agent群集运动控制 ［J］.华中科技大学学报：自然科学版，2005，33（8）：56－58.Yu Hui，Wang Yongji，Cheng Lei.Control of stable flocking motion of multi－agent with a leader［J］.Huazhong University of Science and Technology（Nature Science Edition），2005，33（8）：56－58.

［10］Yu Hui and Wang Yongji.Control of stable flocking motion of multi－agent with a leader［J］.Journal of Huazhong University of Science and Technology，2005，33（8）：56－58.

［11］Yu H，Wang Y J.Stable flocking motion of mobile agents following a leader in fixed and switching networks［J］.International Journal of Automation and Computing，2006，3（1）：8－16.

［12］Yang H Y，Zhang ZH X，Zhang SH.Consensus of mobile multi－agent system with disturbance－observer－based control［J］.Control Theory and Application，2010，27（12）：1787－1792.

［13］刘佳，刘忠信，陈增强.基于时变时滞动态拓扑网络的多智能体鲁棒H∞一致性控制 ［C］∥29届中国控制会议.北京，2010：4512－4517.Liu Jia，Liu Zhongxin，Chen Zengqiang.Robust H∞consensus control for multi－agent system with dynamic topologies and time－varying delays［C］∥ Proceedings of the 29th Chinese Control Conference，Beijing，2010：4512－4517.