中国废旧家电回收市场稳定性及其应用研究

谢 磊，马军海

（天津大学管理与经济学部，天津300072）

0 引言

随着中国经济的快速发展，人民对生活质量要求的提高。家电等生活用品的更新换代越来越快。在以前，家电的处理方式单一，再利用程度不高，不仅造成了材料的浪费，废弃的电子零件还对环境造成了严重的污染。家电回收处理正被越来越多的制造商重视起来。政府也通过补贴的方式对家电回收工作给予一定的支持。过去，制造商一直通过大型零售商（如国美、苏宁等）进行废旧家电的回收工作。在这个过程中，零售商提供回收服务，以赚取部分差价。制造商则通过拆解废旧家电获得可以再次利用的材料进行再生产，节约生产成本，获取一定的经济利益。随着互联网技术的发展，电子商务模式和网络支付技术的逐渐成熟，回收市场上逐渐兴起了网络回收模式，即制造商直接通过自身的回收网站对产品进行回收。于是就与传统回收渠道一起组成了双渠道回收模式，如图1所示。

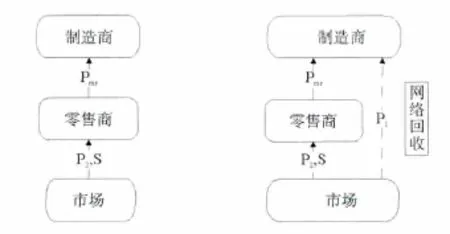
图1 传统单渠道回收模式和双渠道回收模式Fig.1 The traditional single channel and dual channel recovery model

随着电子商务的日趋成熟，网络回收正像网络购物一样逐渐被人们所接受。香蕉皮网（http：／／www.xiangjiaopi.com／）就是这些在线回收网站中比较成熟的一个。对于制造商来说，网上回收可以覆盖更大的回收市场，减少中间商的利润分成。但是与传统回收渠道相比，存在安全性和服务水平的问题，因而消费者对网络回收模式的认可程度一般要差于传统回收模式。有研究发现，不同地域的人民由于消费水平等原因，对电子商务的认可程度并不相同。在2011年，腾讯电商平台公布了各地的消费者购物数据，其中广东、江苏、浙江、山东、北京、福建、四川、湖北、河南、上海等地区的用户分居网络购物量前十位，其中广东地区的用户占比14%，江苏和浙江的用户分别占比7.4%和7%。另外，不同商品的网络认可程度也不相同，如表1所示。

表1 不同产品对应的网络认可度Tab.1 The recognition degree to the Internet of different kinds of goods

对网络回收模式认可度的不同，需要引起回收商的重视，并在制定回收策略时对不同地区区别对待。

国内外有一些学者对废旧电子产品回收的工作进行研究。Shih［1］设计了一个混合整数规划模型来优化基础设施和逆向物流。该模型使得供应链成本实现了最低化。Jae－chun Lee等［2］介绍了韩国对废弃电子设备的回收利用情况及EPR系统在回收过程中的应用。Hainault等［3］介绍了北美垃圾市场回收电子产品中，各个利益群体的努力情况和最终的结果。Kang等［4－5］介绍了美国现有的对电子废弃物回收处理的办法，并介绍了从电子垃圾中提取有价值物品的方法。陈国兵［6］研究了政府和企业在废旧家电回收过程中的作用。分析出了政府的补贴政策对企业决策的影响。罗乐娟等［7］研究了在废旧家电回收过程中，激励机制的构成以及逆向物流的委托代理机制。

在复杂系统理论应用研究方面，国内外学者也做过很多研究。Agiza建立了一个描述多个竞争者的古诺模型的非线性系统，研究了这个系统的均衡解是否存在及其稳定性。JunhaiMa等［8］研究了保险市场三寡头价格博弈和系统复杂性。Zhihui Sun等［9］研究了中国冷轧钢市场的博弈行为的复杂性。HongwuWang等［10］建立了古诺和伯川德混合的双寡头模型，分析了纳什均衡点的存在情况以及博弈系统的稳定性问题。YuehongGuo等［11］研究了由零售商负责销售和回收的闭环供应链系统的稳定性问题，分析了不同博弈模式下各方的利润变化。

1 符号和假设

本文的回收量模型考虑消费者对废旧家电残值的估计。消费者会对废旧家电的残值和回收价格进行权衡。当消费者觉得回收价格和服务的效果低于家电的残值时，会拒绝回收服务，继续使用。Chiang［12］描述了消费者效用决定销售量的方法。类似地，本文也利用消费者效用决定回收量。如果用消费者从第种渠道回收产品的效用，v为消费者对产品残值的估计，pi为回收方i的回收价格，pmr为制造商支付给零售商的内部回收价格。s为零售商提供的回收服务。α为消费者对价格的敏感程度，β为消费者对服务的敏感程度，则消费者通过回收方i回收的效用可以表示为

在传统回收渠道提供回收服务时，会产生一定的成本。Tsay等［13］描述了供应链中提供服务的厂商的服务成本表示法：cs＝ηs2／2。其中，cs为提供服务消耗的成本，η为服务成本系数。η越小，服务的效率就越高。

随着居民生活水平的提高，电子商务模式逐渐被人们所接受。于是网络直接回收模式便应运而生。然而，不同地区的居民由于收入水平和生活环境等诸多因素，对网络电商平台的认可程度并不一致，对网络回收模式的认可度亦有所差别，这个差别体现在对持有的废旧家电的残值的估计上。令网络回收时消费者对废旧家电的残值的估计为，并定义网络认可程度参数θ（0＜θ＜1），则消费者在面对传统回收模式时，对持有的废旧家电的残值估计为vt＝θv。

2 模型分析

在传统的单渠道回收模式的基础上，制造商可以选择是否加入网上直接回收渠道，从而组成双渠道回收模式。另外，主导回收过程的制造商作为强势一方也可以选择与零售商分开决策，或者与零售商合作进行集中决策。因此，本文将分析单渠道和双渠道两种回收模式下，分别采用集中决策和分散决策时，零售商和制造商的利润，以及渠道总利润。

2.1 单渠道回收模式

假设单一渠道下消费者只能选择一种回收途径，受Chiang［12］的启发，令残值估值在上均匀分布，而消费者数量在区间上也是均匀分布。此时当u＞0，有u＜αpr＋βs，因此，回收量可以表示为

表2 本文涉及的4种模式Tab.2 Four modes involved in this paper

单渠道回收模式下制造商和零售商的利润可以表示为

2.1.1 单渠道回收／分散决策

当双方分别决策，并且由于制造商较为强势，而采取以制造商为leader的Stackelberg博弈。作为Follower的零售商首先决策，作为Leader的制造商根据零售商的决策结果来做出决策，于是可以得到最优解：

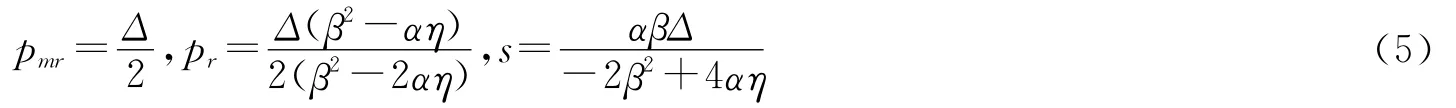
于是，可以得到在单渠道回收，并采取分散决策模式下，双方的最优决策值以及各自的利润、渠道总利润为

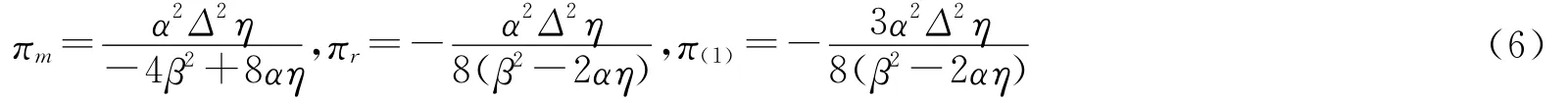
2.1.2 单渠道回收／集中决策

当双方采取集中决策时，以供应链的总利润最大化为目标进行决策，易知，制造商的决策变量pmr只影响制造商和零售商之间的利润分配，并不影响供应链的总利润，因此当联合决策时，只有零售商的决策变量会影响供应链的总利润。于是可以求得零售商的最优决策值，以及供应链的最大利润：

为了满足决策值和利润为非负数，双渠道下各个参数需要满足条件：

2.2 双渠道回收模式

上文提到，很多制造商在原有回收渠道的基础上，加入了网络回收的新的回收模式，从而与传统回收模式组成了双渠道的回收模式。在这个模式中，制造商和零售商既有回收市场上的竞争行为，也有回收过程中的合作行为。制造商和零售商同时在市场中进行回收，消费者有更多的机会依据自身的利益选择对于自己来说效用更大的回收渠道。由于零售商回收渠道可以立即支付、并且给人带来交易安全的感觉等原因，此时消费者对废旧产品的残值估值会低一些，也就是说在相同条件下，消费者对零售商回收模式的效用更大一些。这个估值上的差距定义为直接回收渠道的便捷带来的残值折扣系数，用表示。零售商可以提供回收服务，而制造商无法通过网络回收提供回收服务。此时，消费者对于制造商回收渠道和零售商回收渠道的效用分别为

由此可以判断，消费者对同一件废旧家电残值的估值大小会影响两种回收渠道的效用。首先需要分析一种特殊的情况，即当消费者会只接受零售商回收渠道，此时制造商绝不会愿意开通直接回收渠道，而零售商就不会享受到双渠道回收可能带来的好处。因此零售商也会控制回收价格以不至于彻底打击制造商的直接回收渠道。因此只考虑的情况。

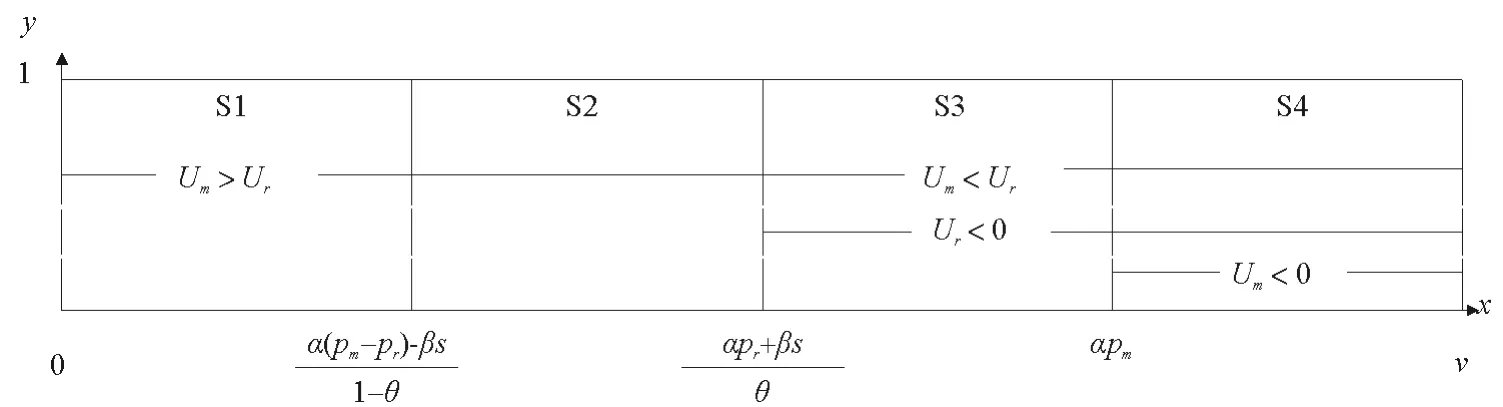
图2 消费者效用区间对应回收量Fig.2 Consumer utility interval and corresponding recovery volume

如果用x轴表示残值，y轴表示区域人口总数，就可以用面积表示回收量［12］。根据上文的分析，x轴可以表示成如下的区间：

在y轴的人数服从（0，1）分布时，回收量可以表示为

因而双方利润可以表示为

2.2.1 双渠道回收／分散决策

采取双渠道回收模式时，采用Stackelberg博弈，制造商为领导者。可以求得制造商、零售商的最优决策以及双方利润和供应链利润的最大值：

2.2.2 双渠道回收／集中决策

在集中决策下，双方都以供应链总利润最大化为目标，零售商和制造商的最优决策值以及总利润的最大值为

为了满足决策值和利润为非负数，双渠道下各个参数需要满足条件：

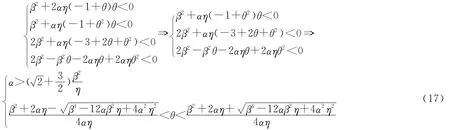
2.3 命题和数值模拟

本小节通过对4种回收和决策方式的比较分析，得出几个很有指导意义的命题，并采用数值模拟的方式直观展现比较的结果以支持部分命题。令α＝0.5，β＝0.2，η＝0.6，Δ＝2。此时可以得到0.144 6＜θ＜0.922 1。

命题1 双渠道回收模式下制造商的利润大于单渠道回收模式，因此作为制造商有开通双渠道回收模式的动机。

证明：由于集中决策时，无法单独算出制造商和零售商的利润，因此只考虑分散决策的情形。此时双渠道回收模式和单渠道模式下制造商利润作差可得：

命题2 双渠道回收模式与单渠道回收模式下，零售商利润的变化情况与当地对互联网回收模式的认可程度以及对回收价格的敏感程度有关。

证明：分散决策时单渠道和双渠道模式下零售商利润作差：

零售商在双渠道下的利润大于单渠道下的利润；

零售商在双渠道下的利润小于单渠道下的利润。

因此零售商是否获得更多的利润是有条件的，与系数θ和α的大小有关。通过图形可以直观看出不同渠道下零售商利润的大小关系随着系数θ的变化。如图3所示：

从图3可以看出，双渠道和单渠道模式下零售商利润大小的关系。θ在［0.144 6，0.561 4］和［0.921 4，0.922 1］两个区间时，双渠道下零售商的回收利润大于单渠道下的。而在区间［0.561 4，0.921 4］上，单渠道的回收利润要大于双渠道的回收利润。

命题3 双渠道回收模式／集中决策下，供应链总利润随着系数θ的增大而先减少后增大。

证明：利润对系数求导可得

双渠道回收模式，集中决策下，供应链总利润随着系数的变化而发生的变化，如图4所示。

一个地区消费者对网络渠道的认可程度会随着互联网技术的发展和自身网购体验次数的提高而逐渐提高。很少会出现网络认可程度逐渐下降的情况。因此作为回收方，需要认可随着消费者网络认可程度的提升，自身回收利润下降的情况。回收方需要做的是最大程度提高消费者的网络认可程度，实现总体利润的“触底反弹”。

图3 不同值θ下零售商在单渠道和双渠道模式下的利润Fig.3 The profit of retailer in single channel and dual channel model with different values ofθ

图4 不同值θ下集中决策双渠道模式下供应链的总利润Fig.4 The total profit in dual channel mode and centralized decision with different values ofθ

命题4 单渠道和双渠道两种模式下，集中决策下供应链的总利润大于分散决策下的总利润。证明：采用做差法，在单渠道模式下，集中决策与分散决策的总利润差值为

于是，有π（2）＞π（1）。

同样，在双渠道模式下，集中决策与分散决策的总利润差值为

于是，有π（4）＞π（3）。

因此，集中决策下供应链总利润总是大于分散决策下。

命题5 分散决策和集中决策下，双渠道回收模式的供应链总利润总是大于单渠道回收模式下的总利润。

证明：分散决策时，两种回收模式下的总利润作差可得：

由于β2＋2αη（－1＋θ）θ＜0，因此β2－6αη（－1＋θ）θ＜0，因此αη（－β2＋6αη（－1＋θ）θ）＞0；

由于0＜θ＜1，故（－1＋θ）（3＋θ）＜0，又因为β2－2αη＜0，因此（β2－2αη）（－1＋θ）（3＋θ）＞0

而（β2－2αη）（β2＋2αη（－1＋θ）θ）＞0，因此Δπ＞0，有π（3）＞π（1）。

同样，集中决策时，两种回收模式下供应链总利润的差值为

由于β2＋2αη（－1＋θ）＜0且－1＋θ＜0，显而易见，β4＋2αη（－1＋θ）（β2＋2αη（－1＋θ））＞0，

因此 Δπ＞0，有π（4）＞π（2）。

因此不论是何种决策方式，双渠道回收模式的总利润必定比单渠道回收模式的总利润大。

由于上文命题5分析到集中决策的总利润总是大于分散决策的总利润，同时，命题6分析到双渠道的总利润总是大于单渠道的总利润。因此可以对四种模式的总利润大小进行排序。有π（4）＞π（3）＞π（2）＞π（1）。通过作图分析系数θ的变化对4个回收模式利润变化的影响，如图5所示。

2.4 保证实施集中决策的合理契约

由于集中决策方式无法确定双方各自的收益，因此需要双方对利润分配进行协商，使得双方最终获得的收益大于双渠道分散决策获得的收益。这种契约可以是双方协定的内部回收价格，也可以是差额利润的合理分配。因此，如果双方签订合适的契约，以供应链整体利润最大化为目标，双方将采取双渠道回收模式，集中决策方式。

为了维持这个模式的顺利展开，需要保证双方集中决策利润都大于分散决策利润。本文考虑采用双方协商的内部收购价格pmr的一个合理区间，满足双方利润都优于分散决策时各自的利润。即需要满足条件：

解不等式组（27）。对其整理可得

根据本文中各个变量代表的实际含义，各个变量都为正数，特别地，0＜θ＜1，因此采用Mathematica软件解不等式组，可以得到：

根据上文可知，文章采用的数值模拟下，的合理取值范围为：0.144 6＜θ＜0.922 1，因此可知，此处满足条件因此可以得到内部收购价格pmr的合理区间为

根据上文的数值模拟，和该组数值对应的系数θ的范围，可以做出合理的pmr价格区间，如图6所示。

在这个合理的价格区间内，双方都可以通过双渠道集中决策获得多于分散决策下获得的收益，因此，双渠道回收模式可以顺利展开。

图5 不同值θ下各种回收模式和决策模式下的供应链总利润Fig.5 The total profits in all kinds of recovery and decision mode with different values ofθ

图6 随着θ值变化的pmr合理价格区间Fig.6 The seasonable price interval of pmrasθchanges

3 系统的稳定性分析

上文分析到采用双渠道回收模式并且集中决策下的利润是最大的。因此文章这部分考察这个系统的稳定性。随着网络认可程度的提高，回收总利润会出现先减少后增大的情况，研究发现，如果厂商的决策变量调整系数过大，系统会在利润未实现提升时就进入混沌状态。这样不利于总体利润最大化的目标，因此需要对该系统进行稳定性分析，并给出一定的混沌控制方法。

3.1 系统模型和求解

由于双方可能不知道对方会采取什么策略，只能选择自身的最优策略，并且根据上一期双方的决策值对本期决策值做出调整，以获取最大利益。因此双方采取重复博弈模型：

令x（t＋1）＝x（t），解方程组。可以求得系统解

可以知道只有R7满足所有决策变量的边际利润为零，即不会主动变化寻求更大的收益。因此R7是唯一的纳什均衡解。得到了唯一的纳什均衡解后需要分析解的局部稳定性。

式（31）的Jacobian矩阵为

根据Routh－Hurwitz稳定性判据，可知解局部稳定的条件需要满足：

因此，通过上述的数值模拟，带入R7的值，可以得到本系统的稳定域，如图7所示。

3.2 系统决策变量的衍化

当制造商的决策调整系数不变（g1＝0.4）时，观察零售商决策变量调整系数的变化对系统稳定性的影响，如图8所示。

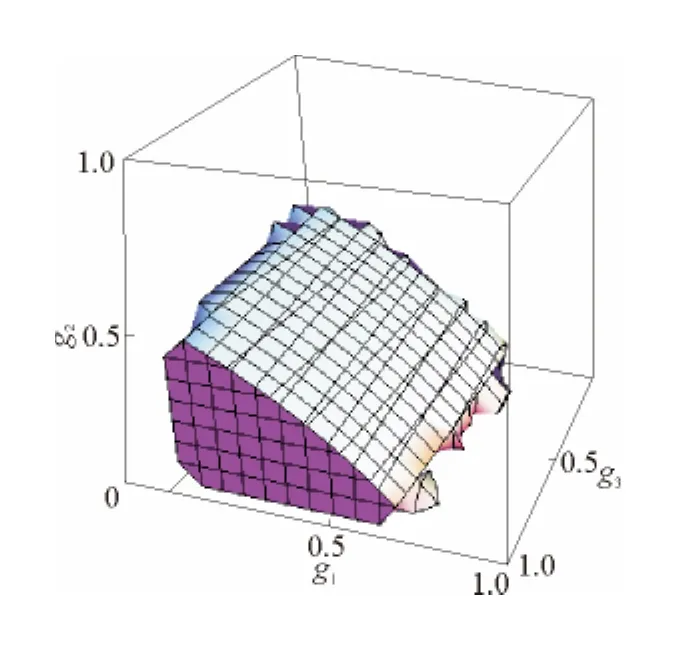
图7 θ＝0.6时，系统的稳定域Fig.7 The stable region of system withθ＝0.6

图8 g1＝0.4时，系统的三维分岔图Fig.8 The three－dimensional bifurcation diagram of system with g1＝0.4

可以看出，随着g2和g3的增长，系统逐渐进入混沌状态。而当g2和g3维持在一个较低的水平时，系统处于稳定状态，形成了一个稳定的平面。

当零售商的决策变量调整系数不变（g2＝g3＝0.3），观察制造商的回收价格调整系数的变化对系统稳定性的影响如图9所示。

图9 系统的分岔图Fig.9 Bifurcation diagram

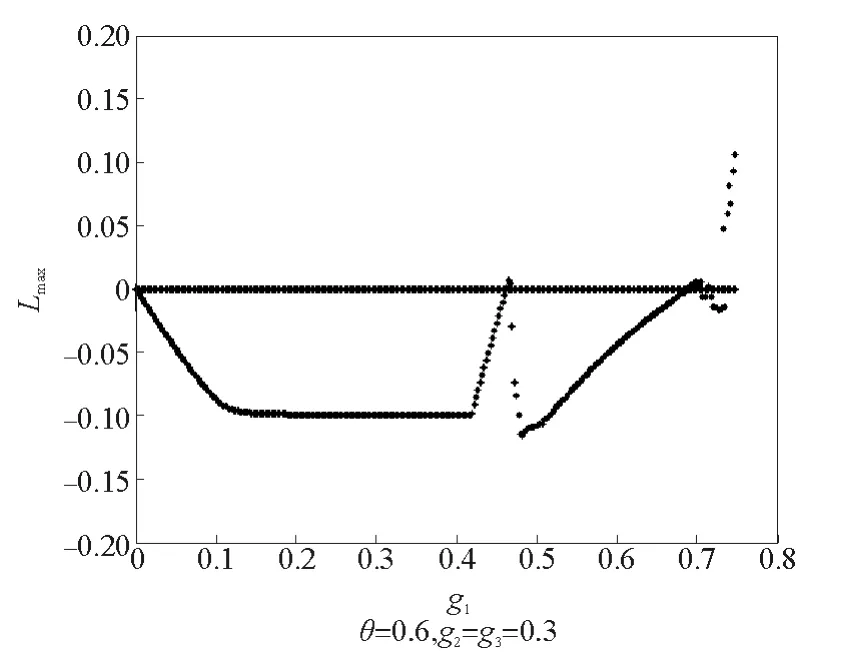
图10 系统的最大Lyapunov指数图Fig.10 The largest Lyapunov exponent

可以看出，随着制造商回收价格调整系数的提高，系统逐渐从稳定状态第一次进入混沌状态，随后进入倍周期分岔状态，最后再次进入混沌状态。这是一种霍普分岔状态。当制造商的回收价格调整速度过快时，系统会进入混沌状态，在这种状态下，供应链上双方都无法得到一个稳定的价格，因此也得不到一个稳定的利润。此时，在零售商的决策变量调整系数固定为g2＝g3＝0.3时，制造商决策变量调整系数的最优决策约为0.46（通过Routh－Hurwitz判据计算得最优值为0.462 257）。因为在这组系数下，回收方既可以保证系统处于稳定状态，又可以保证回收方通过最少次数的博弈，最短的时间达到利润最大化的状态。图10表示系统最大lyapunov指数图，当其值大于0时，系统进入混沌状态，小于0时，系统处于稳定状态。最大lyapunov指数的演化和图9显示出同样的结果，即系统先从稳定状态进入混沌状态，再进入倍周期分岔状态，最后进入混沌状态。

在混沌状态下，各方的决策变量无法得到一个稳定的值。图11和图12分别是不同水平的调整系数（g1＝0.8和g2＝0.7）下，回收方决策变量的时间序列。可以看出当系统处于混沌状态时，制造商和零售商的决策变量会出现不稳定的情况，每个博弈期的决策变量都会出现巨大的差别。回收方无法实现一个稳定的决策和稳定的收益。

图11 决策变量的时间序列Fig.11 The time series of the decision variable

图12 决策变量的时间序列Fig.12 The time series of the decision varible

3.3 混沌吸引子和初值敏感性

图13和图14分别相应水平的调整系数（g1＝0.8和g1＝0.7）下，系统的混沌吸引子。系统的混沌吸引子有一个明显特征就是吸引子外的运动都收敛到吸引子上，而吸引子内部的运动又是相互排斥的。

混沌系统的另一个特征是对初值的敏感，孔令云和樊养余［14］曾分析到相邻状态在同一运动模态中运动的逐渐分离，和在不同运动模态之间的不同时（或不同幅度）转换，导致了系统运动对初值的敏感依赖。本文模拟了在制造商造成的混沌状态（0.8，0.3，0.3）下，制造商初值的微小变化（0.5到0.500 1）经过一定的博弈期后，差值被放大的现象，如图15所示。

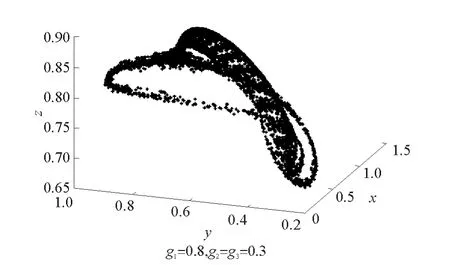
图13 系统的混沌吸引子Fig.13 Chaotic attractor

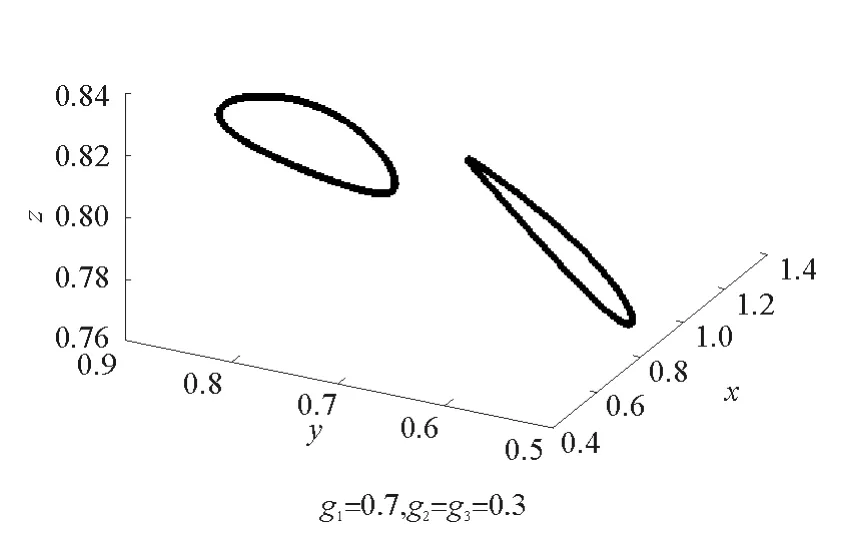
图14 系统的混沌吸引子Fig.14 Chaotic attractor

图15 混沌状态下，初值调整前后p1值的变化Fig.15 The changes of p1after the adjust on initial value in chaotic state

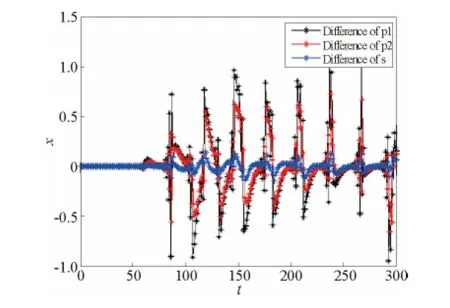
图16 混沌状态下，初值调整前后各决策值的差值Fig.16 The changes of three decision variable after the adjust on initial value in chaotic state

图16中红色和蓝色的点分别表示调整前后各个博弈期的决策值p1，其直观反映出了调整前后各期博弈决策值的差值。当博弈进行到50期以后，初值的微小变化带来后期决策值的差距逐渐显现出来，变动最大时，差值是初始差值的10 000倍。可见如果决策变量调整系数过大，造成系统处于混沌状态下时，初始决策值的微小变动可能使得后期各方的利润产生巨大的变化。

3.4 差异化的网络回收认可度θ对系统的影响

上文分析到系数θ的大小会影响到各方的决策值以及各方的利润。在稳定状态gi（0.46，0.3，0.3），集中决策的双渠道回收模式下，随着θ的变化，各方决策变量和总利润的变化如图17、图18所示。

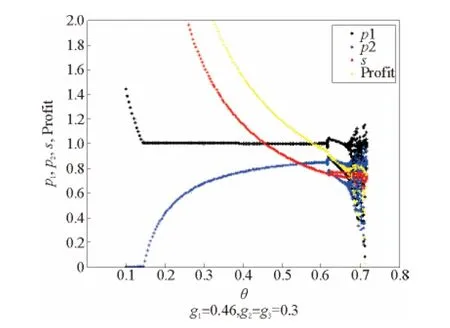
图17 随系数的变化，各个决策值和总利润的变化情况Fig.17 The changes of three decision variables and the total profit asθchanges

图18 随系数的变化，系统的最大Lyapunov值的变化Fig.18 The changes of the largest Lyapunov exponent asθchanges

随着互联网技术的成熟，人们会更加接受互联网回收的模式，对应的系数θ的值会上升。上文分析到，供应链总体利润会随着系数θ的变化而出现先减少后增大的现象。在本文的市场环境下，供应链总体利润的最低值出现在θ＝0.866 7时。在此时零售商采取的决策变量调整系数的水平下，系统总体利润没有触底反弹就出现了混沌状态。因此需要注意的是，不同地区人们对网络回收模式的认可程度不同，对应的系数θ则不同。当θ值过大时，系统会进入混沌状态。如图所示，当θ＞0.6时，系统会进入混沌状态。由g1、g2和g3组成的系统的稳定域，θ的大小决定了稳定域的大小。随着θ的增大，稳定域逐渐减小。最终当θ＞0.7时，系统的稳定域减小到一定程度，使得在原稳定域内部的点gi（0.46，0.3，0.3）落到了新的稳定域之外。造成了系统的混沌状态。图19是在不同θ下，系统的稳定域。可以看出，随着θ的增大，系统稳定域逐渐减小。

图19 θ分别取0.4，0.6，0.8时系统的稳定域Fig.19 The stable region whenθequal to 0.4，0.6，0.8

因此尽管当θ大于一定的水平时，系统总体利润会出现剧烈增长的情况，但是如果决策变量调整系数过大，那么θ的增大很有可能造成混沌状态，无法获得其对应的高利润水平。面对不同地区的回收市场，回收企业要根据其对网络回收模式的认可程度决定其变量调整系数，做到既能最快调整到最优水平，又能保证系统维持稳定状态。针对本文的市场环境，利润最低点处θ＝0.866 67，为了保证系统的稳定和利润的提升，可以计算出此时制造商和零售商决策变量调整系数需要满足的条件。当零售商不针对市场情况作主动调整时，制造商相应的调整策略可以根据Routh－Hurwitz稳定性判据计算出来，如表3所示。

不难看出，随着系数θ的增大，维持系统稳定的变量调整系数g1的范围逐渐缩小。同样，当制造商决策调整系数不变的情况下，零售商的决策调整系数组合也会因为系数θ的变化而变化。整体的稳定域也会随着θ的提高而减少。

表3 不同网络认可度对应的制造商为保持系统稳定需要的条件Tab.3 The condition to maintain the system stability for manufacturer in different recognition degree to the internet

4 混沌控制

当系统处于混沌状态时，会产生很多不利的影响。上文已经分析到，混沌系统会造成决策方决策困难，对初值的设定十分敏感，也无法实现最优利润。因此需要对混沌系统进行控制，常见的混沌控制方法有OGY方法、外力反馈控制法、自适应控制法、模糊控制法等。Elabbasy［15］在三寡头模型中采用反馈控制。本文也采用反馈控制法。仍然假设零售商不做任何调整，制造商进行混沌控制。混沌控制模型如式（35）。

其中，k为控制系数，在一个混沌状态（g1＝0.8，g2＝g3＝0.3）下，混沌系数对混沌控制的效果如图20、图21所示。随着控制系数k的增大，系统逐渐从混沌状态进入稳定状态。

图20 混沌状态的反馈控制下系统演化图Fig.20 System evolution diagram under control in chaotic state

图21 混沌状态的反馈控制下系统最大LyapunovFig.21 The largest Lyapunov exponent under control in chaotic state

5 实际问题分析

本文分析了4种情境下，“双渠道回收模式并采取集中决策模式”的情境下，供应链的整体利润是最优的。文章还引入了复杂系统理论，指出了系统可能存在的系统混沌问题及其危害。这部分，通过对上海和天津两个不同网络认可度的地区关于废旧家电回收的分析，进一步验证文章的结论。

据东方网报道（http：／／www.news365.com.cn／xwzx／gd／201307／t20130711＿1313975.html），在上海很多市区的便利店，都有“阿拉订”家电回收终端机，点击进入后，可以选择屏幕显示的回收家电品类。消费者在终端上预约登记后，24小时内会有客服人员通过电话联系回收事宜，并与消费者确定上门时间等信息。这是传统的回收模式，而上海市商务委正策划一个覆盖全市的电子回收网络，在现有布点的基础上不断扩大。

据《2013年中国网购市场调查报告》（http：／／www.mcqyy.com／wenku／diaochabaogao／10148.html）指出，该年支付宝用户的增长速度远远高于同期中国网民的增长速度，这说明网民对于网购的认可程度是逐渐上升的。报告还指出，2013年全国网购交易量排名前5位分别为：广东、江苏、浙江、上海和北京。相比于一些省级地区，上海人口数量相对较少，而其网购交易量从2011年的全国第10位，上升到全国第4位。可以说上海地区不仅网购人口比例众多，而且发展迅速。2012年，上海市人口约2 380万人，其网上购物人数已经超过300万。按照每个家庭3口人计算，平均每2到3个家庭就有一户家庭愿意接受网购的模式。因此在上海地区，可以将网络认可度系数θ的值定义为0.378（3＊300／2 380）。通过上文分析可知，内部回收价格pmr的区间为（1.155 5，1.311）。假设在回收过程中制造商的地位强于零售商，其规定的内部回收价格为pmr＝1.2。在该地区进行双渠道废旧家电回收工作时，对于整条回收渠道，其采用各种回收方式的获利情况如表4所示。

表4 不同回收渠道和决策模式下制造商、零售商和供应链利润Tab.4 The profit of manufacturer，retailer and the supply chain in different recovery channel and decision modes

通过对比可以清楚看出，选择双渠道集中决策，对制造商、零售商和供应链的总利润都是有利的。双方在这样的共识下可以合作采取双渠道集中决策方式进行废旧家电的回收工作。在该模式下，双方最优的决策值为：p1＝1，p2＝0.753 8，s＝1.230 8。

对于系统的稳定性，当零售商不做任何改变，选择决策变量调整系数的组合g2＝g3＝0.5时，随着制造商决策变量调整系数g1的变化，系统的演化图如图22所示。系统的稳定区域为（0，0.370 4）。对于制造商来说，为了实现尽快达到最大利润，同时保持系统稳定，应采取g1＝0.370 4。

图22 上海实施双渠道回收的系统演化图Fig.22 System evolution of Shanghai practice dual channel recycling

图23 天津实施双渠道回收的系统演化图Fig.23 System evolution of Tianjin practice dual channel recycling

当家电回收企业考虑在其他地区进行家电回收时，需要考虑到当地网络认可程度对回收系统的影响。当在上海地区的回收工作发展的比较成熟，进而进军其他的废旧家电回收市场时，需要对原决策进行适当调整。同时期，天津网购人口为200万人，总人口数为1 400万人。网络认可程度为。此时，双方最优决策值：p1＝1，p2＝0.787 0，s＝1.064 8。本文分析到，随着网购认可程度的上升，如果不对决策变量调整系数进行调整，系统会逐渐进入混沌状态。因此回收方需要对市场进行分析判断，以做出最优的决策，在保证系统稳定性的前提下，获取最大利润。此时，系统决策变量随着制造商决策变量调整系数的变化而演化，如图23所示，系统稳定的条件是g1在（0，－0.328 1）区间。因此对于制造商来说，需要将决策变量调整系数从0.370 4调整到0.328 1，以适应该地区较高水平的网络认可程度。

6 结论

本文建立了由制造商和零售商组成的家电回收模型，分析了不同回收渠道和不同决策方法下，制造商和零售商各自的利润变化。通过分析可以得出结论，集中决策下供应链的整体利润总是大于分散决策下的整体利润。双渠道回收模式下制造商的利润一定大于单渠道回收模式，而零售商的利润变化情况则取决于该地区人们对网络回收模式的接受程度。文章的后半部分基于“双渠道回收模式并采取集中决策模式”的情境，引入了制造商和零售商的重复博弈模型，通过分析决策变量调整系数，指出了可能存在的系统的稳定性问题。通过对系统的稳定性进行分析，指出了混沌系统的危害，并给出了混沌控制方法。

文章最后通过上海地区和天津地区家电回收的实证分析，证明了双回收渠道集中决策的优势，同时分析了不同网络认可度对系统稳定性的影响，以及制造商需要作出决策上的改变。证明回收方如果在不同的对网络回收模式认可度的地区进行回收时，需要相应地进行决策变量调整系数的调整，以保持回收系统的稳定状态。

［1］Shih L.Reverse logistics system planning for recycling electrical appliances and computers in Taiwan［J］.Resources，Conservation and Recycling，2001，32（1）：55－72.

［2］ Lee J，Song H T，Yoo J.Present status of the recycling of waste electrical and electronic equipment in Korea［J］.Resources，Conservation and Recycling，2007，50（4）：380－397.

［3］ Hainault T，Smith D S，Cauchi D J，et al.Minnesota＇s multi－stakeholder approach to managing electronic products at end－of－life［C］／／8th Annual IEEE International Symposium on Electronics and the Environment，San Francisco，CA，2000：310－317.

［4］ Kang H，Schoenung J M.Electronic waste recycling：a review of US infrastructure and technology options［J］.Resources，Conservation and Recycling，2005，45（4）：368－400.

［5］ Kang H Y，Schoenung J M.Used consumer electronics：a comparative analysis of materials recycling technologies［C］／／IEEE International on Electronics and the Environment，Scottsdale，AZ，2004：226－230.

［6］ 陈国兵.政府与企业在废旧家电逆向物流的博弈分析［D］.北京：北京交通大学，2010.Chen Guobing.Game analysis for reverse logistics of waste household appliance between government and enterprise［D］.Beijing：Beijing Jiaotong University，2010

［7］ 罗乐娟，竺宏亮.废旧家电逆向物流的激励机制研究［J］.物流技术，2004（11）：72－74.Luo Lejuan，Zhu Hongliang.Motivation mechanism of reverse logistics of discarded and used family appliance［J］.Logistics Technology，2004，（11）：72－74.

［8］ Ma J，Zhang J.Price game and chaos control among three oligarchs with different rationalities in property insurance market［J］.Chaos：An Interdisciplinary Journal of Nonlinear Science.2012，22（4）：43120.

［9］Sun Z，Ma J.Complexity of triopoly price game in Chinese cold rolled steel market［J］.Nonlinear Dynamics，2012，67（3）：2001－2008.

［10］Wang H W，Ma J H.Complexity analysis of a cournot－bertrand duopoly game model with limited information［J］.Discrete Dynamics in Nature and Society，2013：287371.

［11］Guo Y，Ma J.Research on game model and complexity of retailer collecting and selling in closed－loop supply chain［J］.Applied Mathematical Modelling，2013，37（7）：5047－5058.

［12］Chiang W K，Chhajed D，Hess J D.Direct marketing，indirect profits：a strategic analysis of dual－channel supply－chain design［J］.Management Science，2003，49（1）：1－20.

［13］Tsay A A，Agrawal N.Channel dynamics under price and service competition［J］.Manufacturing ＆Service Operations Management，2000，2（4）：372－391.

［14］孔令云，樊养余.混沌运动对初值敏感依赖的本质原因［J］.计算机工程与应用，2009（32）：1－4.Kong Lingyun，Fan Yangyu.The essential reason of sensitive dependence on initial value of chaotic motion［J］.Computer Engineering and Applications，2009（32）：1－4.

［15］Elabbasy E M，Agiza H N，Elsadany A A.Analysis of nonlinear triopoly game with heterogeneous players［J］.Computers ＆ Mathematics with Applications，2009，57（3）：488－499.