基于复合策略的社会学习模型

刘坤坤，魏新江，方爱丽

（鲁东大学数学与统计科学学院，山东 烟台264025）

0 引言

在日常生活中，人们对于各类经济、社会、文化事件都会有自己的信念（或观点）。由于信念（或观点）在很大程度上影响着人们的行为与决策，因此研究信念（或观点）的形成与演化是一个具有重要意义的课题。每个个体都可能从社会网络中获取其他个体的观点，还可能接收到反映事件潜在状态的外界信号，并在此基础上更新自己的信念，新的信念再次融入社会网络中，如此不断学习、更新，推动整个群体信念的动态演化。这种个体通过交流与互动调整自己信念的过程就称为社会学习。

社会学习理论［1］是由美国心理学家阿尔伯特·班杜拉于1976年提出的，到目前为止，已经应用到社会学之外的众多领域。对于许多社会问题人们往往想获取一个统一的最佳答案，在当今大数据的网络时代，与这些问题相关的信息往往分散在巨大的社会网络中，社会学习的目的就在于通过个体之间的相互作用使得分散的信息得以整合［2－8］，最终在这些社会问题上达成共识。

社会学习的研究一般是以具体的模型为导向，在不同的问题上所建立的模型也有所区别，比较常见的两种模型，一是基于贝叶斯法则的社会学习，二是基于邻居信念的社会学习。

基于贝叶斯学习的经典研究有很多，从序列社会学习模型［9－10］到社会网络模型［11－14］，基于贝叶斯法则的学习策略在现实生活中的应用越来越广泛。然而，在很多情况下，每个个体仅能够知道很少的其他个体（比如朋友、同事或者家人）的观点，甚至可能仅仅掌握自己的经验。这种有限的观察力，加上由整个网络上分散信息所产生的观点与观点之间复杂的相互作用，使得个体无法以贝叶斯方式学习别人的观点。另外，基于贝叶斯法则的社会学习需要掌握网络结构的完整信息，因此计算的复杂程度相当大。实际上，人们做决策时，并不一定会理性地遵循贝叶斯法则，也有可能采取从众或接受朋友的影响。基于邻居信念的更新策略，初始的经典研究是DeGroot于1974年提出的模型［15］，结果发现，在适当的条件下群体信念能够收敛到一致，但是却不一定收敛到真实信念。人们还就基于邻居信念的社会学习做了后续研究［16－19］。Golub和Jackson在DeGroot模型基础上进行研究，得到进一步的结论：当网络规模无限增长时，如果社会中不存在有影响力过大的个体，那么这种渐近一致的信念将收敛到真实信念［20］。虽然基于邻居信念的更新策略建模比较简单计算也不复杂，但是不能保证个体的信念一定收敛到真实信念，即使能够收敛到真实信念也必须满足网络是无限增长等特定的条件，这就限制了基于邻居信念的更新策略在社会网络中的普遍使用。

由此可见，单独使用基于贝叶斯法则的更新策略或者基于邻居信念的更新策略，都存在着一定的问题，所以我们考虑在社会学习策略中将二者结合起来。2012年，Jadbabaie等［21］在研究社会网络中个体信念更新过程中，个体的信念更新将由个体自己的信念和其邻居的信念共同决定，其中个体自己的信念由贝叶斯法则更新，理论结果表明如果满足网络是强联通的等条件，那么所有个体最终能够达到渐近学习。他们还进一步说明，在强连通的社会网络中，社会交流可以整合出全局的基本状态信息，这种信息整合能够避免使用贝叶斯法则更新带来的计算成本，并且这个模型可以在有限规模的网络中使用，网络的拓扑结构和个体的影响力程度都不能阻碍社会学习，这就避免了单独使用上述任何一种策略带来的问题。Ali Jadbabaie等所使用的模型，要求每一时刻的信念更新时个体自己的信念必须由贝叶斯法则进行更新，个体与邻居之间必须要交流，但是考虑实际情况社会个体不一定每次都要采取贝叶斯法则更新。本文考虑社会个体的异质性和复杂性，提出了一种复合策略。个体在更新信念的过程中，每一时刻个体依据一定的概率选择两种策略之一进行自己的信念更新，或者采用贝叶斯更新策略，或者根据社会网络中邻居信念来更新的策略，而在下一时刻，个体还要依概率选择两种策略之一进行信念更新，并且每个个体的策略选择概率是不同的，这就体现了个体的多样性和复杂性，与实际社会中个体的动力学行为相符，在此基础上建立的模型与Ali Jadbabaie的模型相比更能体现出个体的主观选择性。这种基于复合策略的社会学习模型能够更好地体现社会网络中个体的复杂行为，更好地展现社会个体的信念学习过程。

1 模型

1.1 预备知识

社会网络可抽象为图G＝ （N ，E），其中N＝ ｛1，2 ，…，n｝为社会网络中所有个体的集合，E为个体之间相互作用构成的边集合。个体之间相互作用的权重矩阵记为Q＝（qiij）n×n，qij代表个体i与个体j之间的相互作用权重，对∀i，满足若个体i和个体j之间有直接的相互作用，则qij＞0，就称个体i与个体j互为邻居，若个体i和个体j之间没有直接相互作用，则qij＝0，个体i的所有邻居的集合记为Ni＝｛j｜qij＞0｝。

所有可能的状态的集合记为Θ＝｛θ1，θ2，…，θK｝，其中潜在的真实状态θ＊∈Θ。个体i在t时刻对状态θk的信念表示为Pi，t（θk），初始信念为 Pi，0（θk）。个体所接收到的信号集合为st＝｛s1，t，s2，t，…，sn，t｝∈S1×S2×…×Sn≡S，是根据似然函数P（st｜θ）产生，其中si，t∈Si表示个体i在t时刻观察到的信号，Si表示个体i的信号空间。Pi（·｜θ）为P（st｜θ）的第i个边缘分布，称为个体i的信号结构。这里假设每个个体的信号结构都是已知的。

1.2 更新策略

1）基于贝叶斯法则的更新策略：个体i在t＋1时刻接收到信号si，t＋1，对于状态θk的信念按照下列贝叶斯法则更新：

2）基于邻居信念的更新策略：由于网络中个体之间的相互影响，每一时刻，个体都会综合邻居的信念对自己的信念进行更新，个体i基于邻居信念的更新策略公式为

其中，权重值qij也可理解为个体i对个体j的信任度，特别地，当i＝j时，qii为个体i的自信度。

在社会网络中，个体并不一定完全理性，也不一定完全非理性，因此个体进行信念更新时，并不一定都采取基于贝叶斯法则的更新策略，也不一定都采用基于邻居信念的更新策略，可能有的个体采用贝叶斯更新，有的个体采用基于邻居信念更新，我们提出一种复合策略模型，定义一个个体策略选择概率αi，根据个体的异质性，假定每个个体的策略选择概率αi是不相同的，社会网络中的个体会以概率αi选择贝叶斯更新策略，以概率1－αi选择基于邻居信念的更新策略，即在t＋1时刻个体i的信念更新复合策略为

1.3 定义及命题

定义2 等价观测状态：若个体i在状态θm和θn的条件下的信号结构相同，即Pi（·｜θm）＝Pi（·｜θn），则称个体i不能识别状态θm和θn，状态θm和θn为个体i的等价观测状态。

假如所有个体对状态空间Θ＝｛θ1，θ2，…，θK｝中某两个状态等价观测，那么所有的信号失去了对这两个状态的辨别能力，个体也就失去了接收到信号的意义，所以本文假设不存在对所有个体来说都等价观测的状态。命题1 假设真实状态为θ＊

1）策略选择概率αi：0＜αi≤1

2）社会网络中至少有一个个体对真实状态的信念为正，即∃i∈N，使Pi，0（θ＊）＞0

3）不存在对所有个体来说都等价观测的状态

在上述的条件下，按照复合策略法则（3）进行信念更新，则所有个体都能达到渐近学习。

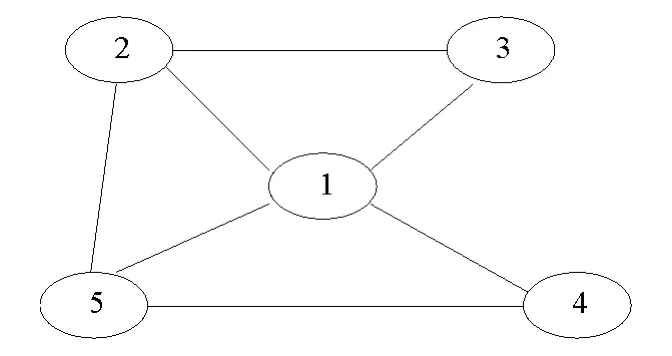
图1 含有5个个体的社会网络Fig.1 A social network with 5agents

2 仿真

在仿真实验中，设定若每个个体对于真实状态的信念满足Pi，t（θ＊）＞0.999 9，则认为所有个体达到了渐近学习，时刻t为达到渐近学习的时间。以图1所示社会网络为例，N＝｛1，2，3，4，5｝ ，状态空间Θ＝ ｛θ1， θ2｝，假定θ1为真实状态，每个个体所接收到的信号是相互独立的，为简单起见，假设个体的信号空间相同，都为Si＝ ｛s1，s2，s3，s4｝，个体的信号结构也相同，设为

给定每个个体的初始信念为

假设个体之间相互作用的权重在它和其邻居之间平均分配，若个体i邻居的数目为di，即它的度数为di，计算权重时要加上个体本身，则个体i与其邻居相互作用的权重值如图1个体1邻居数为4，它的度数d1＝4，它及其邻居相互作用的权重值q1j全部等于，在每次更新的过程中，权重值保持不变。同理得到所有个体之间的相互作用权重，从而相互作用权重矩阵Q为

为了体现个体的异质性，以及观察策略选择概率对于社会个体的影响，对于策略选择概率αi选择4种不同的取值范围，对上述实例利用复合策略法则（3）进行信念更新，得到仿真结果如图2所示。

图2 在不同的策略选择概率下，社会个体信念的演化图Fig.2 The evolution of social individuals′beliefs under different strategy selection probabilities

从上述仿真结果可以看出：1）在满足命题1条件下，所有个体对真实状态的信念最终都能收敛到1，即所有个体都达到了渐近学习，从而整个社会也就达到了渐近学习；2）当策略选择概率在不同的取值范围时，整个社会达到渐近学习的时间不同。

为了体现策略选择概率对于学习速率的影响，对策略选择概率所处的范围进行划分，分别对处于不同取值范围策略选择概率下的学习时间取了500次实验平均，结果如表1所示。

表1 策略选择概率在不同的取值范围下，个体达到渐近学习的时间Tab.1 Individuals′asymptotic learning time under different ranges of strategy selection probabilities

从表1可以直观地看出，每个个体的策略选择概率αi取值越小，即选择基于贝叶斯法则更新策略的个体较少时，虽然最后也能达到渐近学习，但是所花的时间比较长；每个个体的策略选择概率αi取值越大，即选择基于贝叶斯法则更新策略的个体较多时，学习的速度是最快的。也就是说策略选择概率与学习时间呈负相关关系。

3 结论

人类的社会学习，是在复杂的社会环境中进行的，考虑社会网络的复杂性以及个体的异质性，我们采用复合策略去研究个体的社会学习，才与人类动力学行为相符。本文将基于贝叶斯法则的更新策略和基于邻居信念的更新策略结合起来，让每个个体合理选择策略，既能发挥个体的主观能动性，又能与外界环境相交流，研究结果发现，满足一定条件时，社会网络中的每个个体都能够达到渐近学习，并且每个个体的策略选择概率取值越大，渐近学习的速度也越快。

基于复合策略的信念更新，更加符合人们在现实生活中所进行的学习，跟单一策略相比较，得到结果更确切且更加符合人们的认知。但是还有些问题有待于继续探讨：1）本文只是选择双策略进行研究，是否还可以加入其他策略有待于进一步研究；2）个体之间相互作用的权重值，在每次信念更新时，是保持不变的，但在实际生活中由于每次信念更新之后，个体会对邻居又加强了了解，所以在分配权重的时候可能会发生相应的变化，这也是下一步需要考虑的问题；3）本文仿真实验中，假定是不存在顽固个体或者是具有较大影响力的个体，对于这些个体的存在是否能影响到社会网络中个体达到渐近学习，以及即使达到渐近学习是否又影响到学习的速率，这也是以后将要研究的问题；4）文中采取的只是以无向网络为例，对于含有较少个体的网络做了初步的研究，其中社会个体是可以达到渐近学习的，进一步地，有向社会网络中的社会学习问题也亟需探讨。

［1］ Albert B.Social learning Theory［M］.London：Prentice Hall，1976.

［2］ Lee I.On the convergence of informational cascades［J］.The Journal of Economic Theory，1993，61（2）：395－411.

［3］ Tsitsiklis J N，Athans M.Convergence and asymptotic agreement in distributed decision probl－ems［C］.IEEE Transactions on Automatic Control，1984，29（8）：690－696.

［4］ Feddersen T，Pesendorfer W.Voting behavior and information aggregation in elections with private information［J］.Econometrica，1997，65（5）：1029－1058.

［5］ Foster A，Rosenzweig M.Learning by doing and learning from others：human capital and technical change in agriculture［J］.The Journal of Political Economy，1995，103（6）：1176－1209.

［6］ Celen B，Kariv S.Observational learning under imperfect information［J］.Games and Economic Behavior，2004，47（1）：72－86.

［7］ Borkar V，Varaiya P.Asymptotic agreement in distributed estimation［C］.IEEE Transactions on Automatic Control，1982，27：650－655.

［8］ Udry C，Conley T.Social learning through networks：the adoption of new agricultural technologies in ghana［J］.American Journal of Agricultural Economics，2001，83（3）：668－673.

［9］ Banerjee A.A simple model of herd behavior［J］.The Quarterly Journal of Economics，1992，107（3）：797－817.

［10］Smith L，Sørensen P.Pathological outcomes of observational learning［J］.Econometrica，2000，68（2）：371－398.

［11］Gale D，Kariv S.Bayesian learning in social networks［J］.Games and Economic Behavior，2003，45（2）：329－346.

［12］Banerjee A，Fudenberg D.Word－of－mouth learning［J］.Games and Economic Behavior，2004，46（1）：1－22

［13］Celen B，Kariv S.An experimental test of observational learning under imperfect information［J］.Economic Theory，2005，26（3）：677－699.

［14］Montrey M R，Shultz T R.Evolution of social learning strategies［C］.2010IEEE 9th International Conference on Development and learning，Ann Arbor，MI，USA，2010：95－100.

［15］DeGroot M H.Reaching a consensus［J］.Journal of the American Statistical Association，1974，69（345）：118－121.

［16］Ellision Glenn，Fudenberg D.Rules of thumb for social iearning［J］.The Journal of Political Economy，1993，101（4）：612－643.

［17］Ellision Glenn，Fudenberg D.Word－of－mouth communication and social learning［J］.Quarterly Journal of Economics，1995，110（1）：93－125.

［18］Bala V，Goyal S.Learning from neighbors［J］.Review of Economic Studies，1998，65（3）：595－621.

［19］Bala V，Goyal S.Conformism and diversity under social learning［J］.Economic Theory，2001，17（1）：101－120.

［20］Golub B，Jackson M.Naive learning in social networks and the wisdom of crowds［J］.American Economic Journal：Microeconomics，2010，2（1）：112－149.

［21］Jadbabaie A，Molavi P，Sandroni A，et al.Non－Bayesian social learning［J］.Games and Economic Behavior，2012，76（1）：210－225.