基于持续关注度衰减的重要论文预测

张美平，尚明生

（电子科技大学互联网科学中心，成都611731）

0 引言

如何评价科学家的影响力及论文的内在质量一直都是重要的研究课题［1］。基于总引用次数的评价方法最简单但存在若干不足，为此Hirsch［2］提出了具有很强鲁棒性的H指数。此后，Egghe［3］提出g指数用来解决H 指数存在的一些问题。文献［4］提出带权重的PageRank算法对科学家的影响力进行排名。文献［5］基于数字图书馆的引证数据，以科学家合作网络为研究对象，从网络结构特性的角度对科学家进行评价。然而，这些研究大多仅依赖于论文当前的被引次数来评价一篇论文的受欢迎程度和权威性，从而对科学家进行评价，无法处理论文将来可能获得大量引用的情况。因此，如何对论文的潜在重要性进行预测引起了大量学者的关注，已经提出很多算法，主要包括以下3个方面：

1）基于时间效应的方法。科学论文发表时总是会引用已经发表过的论文，因此论文引用次数是随时间动态变化的累计增量。Medo等［6］通过分析论文引用随时间的演化过程和偏好依附过程来挖掘论文的影响力，发现了论文的影响力随着时间指数递减的规律。文献［7］基于引用存在的时间进行加权，为较新的引用赋予较高的权重。Walker等［8］的CiteRank算法优先访问发表时间较近的论文。

2）基于论文多种信息融合的方法。与一般作者相比，领域权威作者所撰写的论文更可能吸引同行的关注；被这些作者引用的论文，也更可能被其他人引用；而发表在影响力更高的期刊上的论文，会更有机会被其他工作者引用［9］。基于这些因素，研究者们运用论文的多种信息，如期刊、作者、领域等信息来更全面地预测论文被引变化趋势。例如，文献［10］利用论文、作者、期刊信息，为不同的引证边赋权，提出一种运用于不同期刊的论文和作者的评价指标。文献［11］利用HITS算法［12］的思想，通过作者－论文关系、论文－论文引用关系以及作者合作关系来动态评价论文的价值以及作者的权威度。此外，文献［13］通过一个加强的泊松分布概率模型来预测论文被引用的动态特性。

3）时间衰减和多源信息融合集成的方法。论文的时间衰减因素通常也和论文的多源信息在一起被考虑。例如，文献［14］依据施引论文所在杂志的影响因子以及引用时间，为引用链接赋予不同的权值，进而评价论文的价值。文献［15］提出FutureRank算法，该算法基于HITS算法［12］与PageRank算法［16］考虑了论文的发表时间、作者权威度和论文当前的PageRank值，基于迭代运算预测论文未来的被引次数排名和PageRank值排名，较之前的算法取得了更好的预测准确度。

上述方法大多存在计算复杂或精确度不高的问题，本文通过对APS和arXiv两个典型数据集的实证研究，发现论文未来引用数和论文的持续关注度密切相关，结合论文引用随时间指数衰减的特性，设计了基于持续关注度衰减的重要论文预测方法。该方法具有预测准确率高，且复杂度低的特点。

1 基于持续关注度衰减的重要论文预测

对科学引文网络的分析需建立在真实数据的研究上。为此，以两个典型的引文网络数据arXiv数据集和APS数据集为研究对象做实证分析和算法研究。其中，arXiv数据集取自arXiv中的高能物理理论引文网络数据集，包含了1992年～2003年发表的所有高能物理论文。APS数据集取自美国物理学会出版的物理评论系列期刊的引用数据集。该数据集论文时间跨度为1893年－2009年，包含了APS系列所有期刊论文的引用关系数据。由于其各期刊的起始时间和数量等因素差别较大，在后续讨论中，仅选取其中异质性较低的PRA、PRB、PRC、PRD和PRL期刊的相互引用关系数据进行实验，简称为APS数据集。经过预处理后，两个数据集的基本信息表如表1所示。

表1 数据集基本信息表Tab.1 Information of the two data sets

1.1 论文的持续关注度

论文发表以后，会有后续论文对其进行引用。这些引用行为反映出科研工作群体对某篇论文的关注程度，可以用论文的引用次数来刻画论文的被关注度。一般而言，论文存在时间越长，被其他工作者关注到的机会就更多［17－18］。因为即使两篇论文质量相当，发表时间长的论文通常会比近期发表的论文获得更多的引用，也即被关注度越大。这样，论文的被关注度是受到时间因素的影响的。为消除这种时间因素带来的影响，本文提出论文持续关注度的概念，用来预测论文未来的被引用情况。论文的持续关注度定义为

其中，S为示论文获得的持续关注度，cc为论文当前获得的总被引用次数，tc为当前时间，tp为论文的发表时间，均以年为单位计算。

通过对APS和arXiv引文数据的实证分析发现，与论文当前总被引用次数相比，论文持续关注度更能体现论文未来的被引潜力。图1a给出了arXiv数据集中论文2000年前的持续关注度与2000年后的持续关注度之间的相关性；图1b显示了相同情况下论文当前总被引次数与未来被引次数之间的相关性。可以看到，相比于图1b，图1a中的点更集中在对角线周围，也就是相关度更高。事实上，持续关注度的相关系数为0.77，而总被引次数的相关系数为0.62，也就是说，论文的持续关注度更能刻画论文未来的引用情况。对APS数据集的分析（见图2），得到类似的结论，前者的相关系数为0.52，后者为0.38。

进一步，本文用持续关注度对论文的未来引用进行预测。图3给出了仅用持续关注度排名来预测论文未来的被引次数排名的实验结果：对前50篇论文，在arXiv数据集上精确率可达0.38，在APS数据集上为0.4。作为对比，如果用当前总被引次数来预测论文的未来排名，arXiv数据集上精确率仅为0.3，APS数据集为0.26。

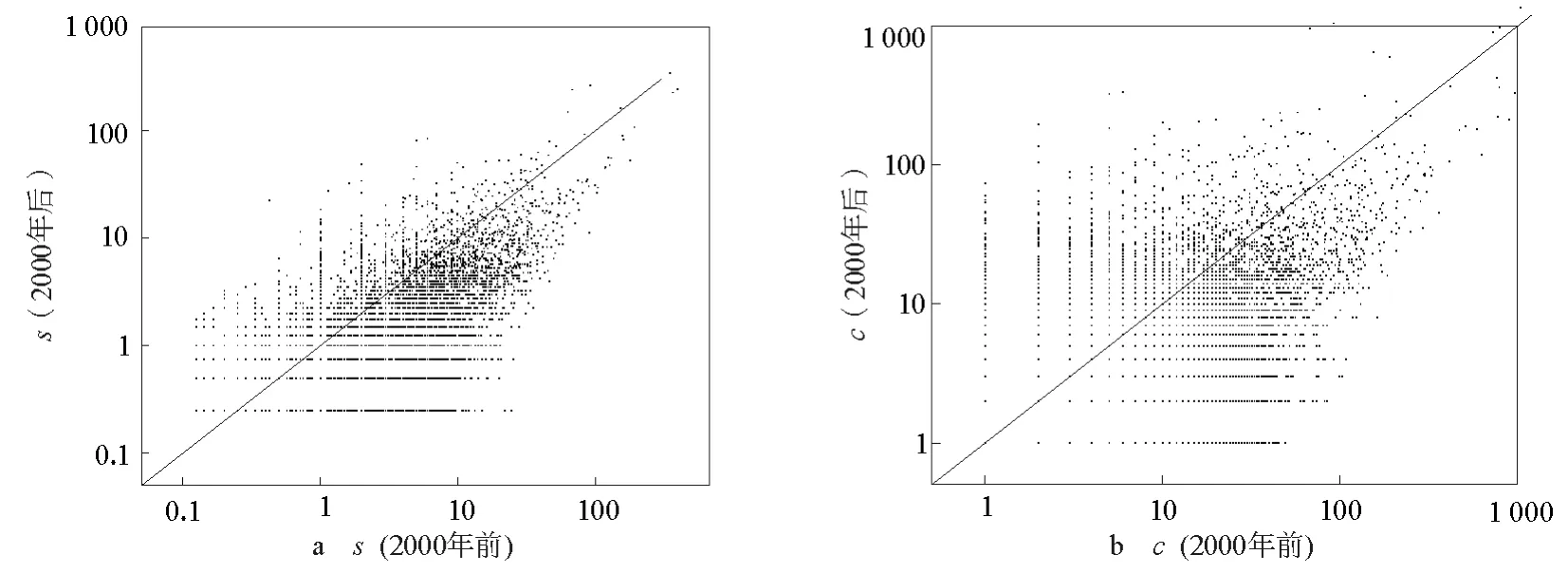
图1 arXiv中论文2000年前和2000年后的持续关注度的相关度和被引总数的相关度Fig.1 Relevance of the sustained attention and the total citations before 2000and after 2000in arXiv dataset

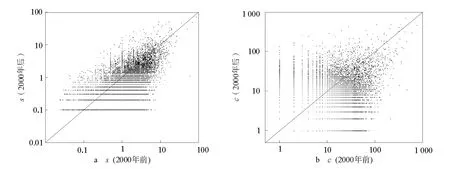
图2 APS中论文2000年前和2000年后的持续关注度的相关度和被引总数的相关度Fig.2 Relevance of the sustained attention and the total citations before 2000and after 2000in APS dataset

1.2 论文的时间衰减效应

论文引用受时间衰减效应的影响已被大量学者的实证研究所证实［6－8］。通常情况下，一项研究成果问世之后，会受到很多同行工作者的关注，但随着时间的推移，新的研究成果会涵盖、完善甚至完全代替已有的研究成果，人们将会更关注这些新的研究成果。除非是开创性工作的论文或者非常经典的文献，才会在经过很多年后依然被大量引用。事实上，我们对arXiv和APS引证数据集的实证研究也支持这一结论。

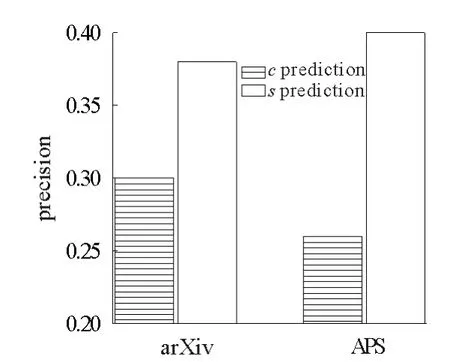
图3 基于持续关注度和总被引数在预测论文未来引用排名的精确率比较Fig.3 Comparision of the predicted precision based on sustained attention and total citations

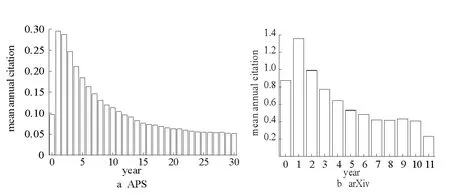
图4 论文引用次数随时间变化图Fig.4 The citation vary over time

图4给出了论文平均引用次数随时间的变化情况，其中横坐标是论文被引用的时间间隔，纵坐标是对应时间的论文平均被引次数。图4a是APS数据集上1958年到1988年发表的论文在30年内的平均被引次数。可以看到，论文平均被引次数是随时间呈负指数规律衰减的。图4b给出了arXiv数据集上的所有论文引用数据的分析。由于arXiv数据集论文时间从1992年到2003年，时间跨度较短，我们统计了其11年的平均引用次数，得到了类似的结论。

1.3 基于持续关注度衰减的论文价值预测算法

通过前面的分析发现，论文的持续关注度体现了论文未来的被引潜力，与此同时，论文引用又呈现明显的时间衰减特性，因此，我们考虑将上面两个因素结合起来对论文未来被引情况进行预测。

沿用文献［8］和［15］中刻画时间衰减效应的指数函数：

其中，x为论文发表时间距离当前时间的年数，ρ为刻画时间衰减程度的参数，其值越大则刻画时间衰减因素权重越大，反之越小。

科学论文发表时，往往会基于不同的引证动机引用相关参考文献。针对这些引用行为，从微观角度同等对待每一条边，仅基于时间为它们赋权则会有失偏颇；但是如果从宏观角度将一篇论文某个时间周期的被引次数作为研究对象，就能降低相应的预测误差。因此，与之前研究对每条引用连边基于时间赋权不同，本文基于时间段为论文的持续关注度赋予不同的权重，进而预测论文未来的被引次数。具体计算公式为

其中，cf为论文未来引用的预测值，tc为当前时间，tp为论文发表时间，ct为该年的被引次数。

2 实验及结果分析

为了验证算法的预测效果，通过arXiv和APS两个典型的引文数据集对算法进行评估。参考算法是目前预测效果最好的FutureRank算法［15］，从算法对参数的敏感度、算法排名预测的准确率和全局的spearman秩相关系数值等3个方面进行对比。

2.1 实验数据和设置

在算法验证过程中，将ArXiv数据集分为两部分：2000年以前的引用数据和2000年以后的引用数据，第1部分为训练数据，第2部分为测试数据。算法的目的是预测论文未来的被引次数和PageRank值排名。其中，被引次数反映论文的流行度，PageRank值反映出论文的权威值［15］。APS数据划分方式类似arXiv数据集，以2000年为分界点划分数据集。两个数据集经过划分之后，基本信息如表2。

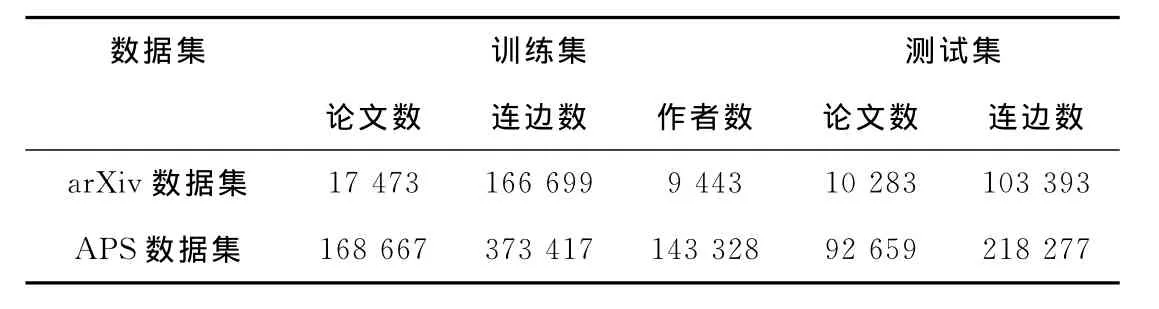
表2 实验数据划分信息表Tab.2 The training data and the test data

2.2 评价指标

2.2.1 精确率

精确率反映算法预测的准确性，定义为

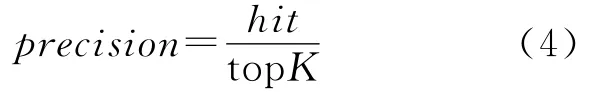
其中，hit＝｜预测排名topk∩真实排名topk｜，精确率用来检验算法对排名靠前的论文的预测准确度。

2.2.2 spearman秩相关系数

计算算法预测的论文未来引用排名、PageRank值排名与论文未来实际排名的全局相关程度。假设测试集中的论文xi，yi按从大到小的顺序排列，记x’i，y’i为xi，yi根据预测算法计算获得的排名，则Spearman秩相关系数的计算即为秩次之间的Pearson的线性相关系数：

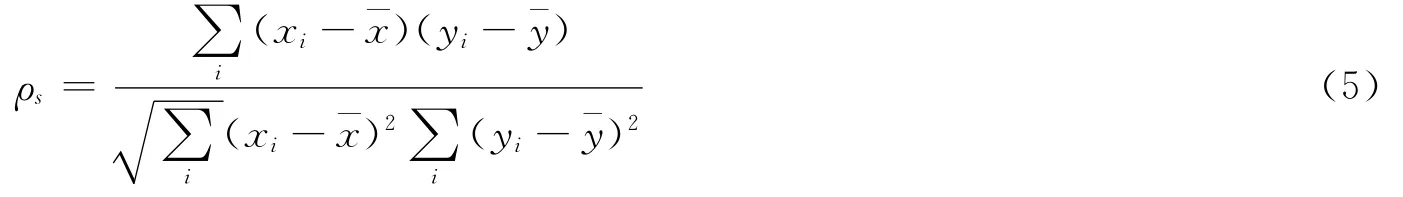
2.3 实验结果及分析

2.3.1 参数敏感性分析

对本文算法中唯一的刻画时间衰减程度的参数ρ，研究其不同取值对算法精度的影响。实验中，不失一般性，topK取值为50（事实上，在实验过程中发现，topK取其他值会得到同样的结论）。

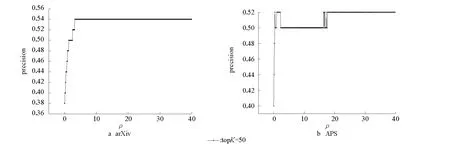
图5 算法预测精度和参数的关系Fig.5 The precision varies over the parameter

图5给出了在两个不同的数据集上，参数ρ的不同取值对算法效果的影响。ρ从0取值到40，取值越大，则刻画时间衰减因素的权重越大，反之越小。当ρ取0时，算法退化成仅用论文持续关注度进行预测，即不考虑时间衰减效应。在arXiv数据上，ρ取值在0到4时，算法效果逐渐提升，考虑时间效应确实大大提高算法预测精确率。此后，算法一直保持最优值，对算法参数不再敏感（见图5a）；在APS数据集上，ρ取值在0到1时，算法精度逐渐提高。取值大于1后，算法一直保持较高精度。在两个不同的数据集上，算法对参数ρ在一定取值后就不再敏感，表现大体一致。需要说明的是，算法对ρ取值的不敏感不代表时间效应因素的不重要，因为曲线前期精确率有一个逐渐提升过程。

2.3.2 算法预测准确性比较

2.3.2.1 不同topK 下的算法精确率

进一步验证算法在不同topK下的预测效果：固定ρ取值最优的情况下，变化topK计算算法精确率，比较本文算法与FutureRank算法［4］、Neman［19－20］提到的用z－score预测论文流行度的算法（仅用来预测论文的被引次数，不预测论文的PageRank值）的预测效果。

如图6a所示，在APS数据集上，对基于持续关注度衰减算法（s－decay）取在topK为50时精确率最高的参数两组ρ＝2.2和ρ＝25，对于FutureRank算法，也取topK 为50时精确率最高的参数两组，futurerank＿1（α＝0.09，β＝0.25，γ＝0.66），futurerank＿2（α＝0.12，β＝0，γ＝0.88）。其中，α为论文当前的PageRank值的权重值，β为作者权威值的权重值，γ为时间效应权重值。由于训练集有将近20万篇论文，所以图中topK取值为1～500。可以看到：z－score的预测结果最差，而基于持续关注度衰减算法在前70名精确率略微高于FutureRank算法，70名后远优于FutureRank算法；基于持续关注度衰减算法在不同参数下，表现几乎一样，FutureRank算法不同参数表现差异比较大。PageRank值预测（见图6b）中，前170名中两种算法差别不大，但170名后，本文算法开始优于FutureRank算法，当topK取值为170到500时，基于持续关注度衰减算法已经远优于FutureRank算法。

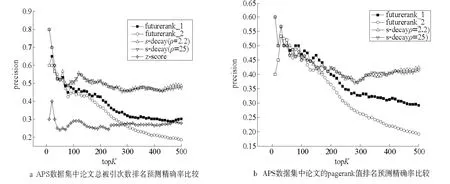
图6 APS数据集的算法精确率比较Fig.6 Comparision of the precision in APS data set

由于arXiv数据的训练集中只有将近2万篇论文，所以图中topK取值从1取到50。基于持续关注度衰减算法在arXiv数据集上ρ大于4后未出现波动情况（2.3.1节），所以只选取ρ＝10这一组值，而FutureRank算法参数仍选择两组，futurerank＿1（α＝0.16，β＝0.05，γ＝0.79），futurerank＿2（α＝0.17，β＝0，γ＝0.83）。从图7a可以看出，z－socre预测效果最差，基于持续关注度衰减算法在不同的topK下均优于FutureRank算法，尤其在20名之后远优于FutureRank算法。图7b显示基于持续关注度衰减算法对论文PageRank值的预测相比于Future－Rank算法同样能获得更高的准确率。

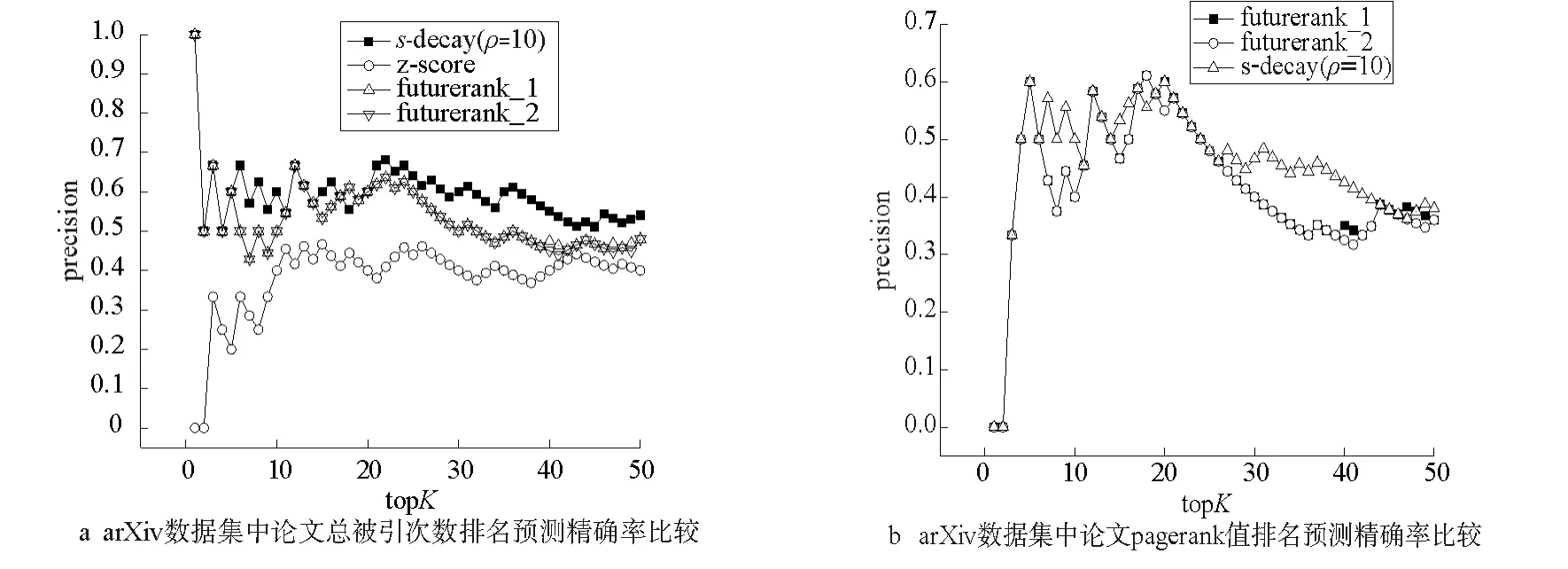
图7 arXiv数据集的算法精确率比较Fig.7 Comparision of the precision in arXiv data set

2.3.2.2 spearman秩相关系数比较

为了验证算法的全局排序效果，对比算法对所有论文的预测排名与其未来的真实排名的spearman秩相关系数。实验结果如图8所示，可以看出，两个数据集上的实验结果显示的结论一致：对于未来被引次数的排名预测，基于持续关注度衰减算法要远优于FutureRank算法，对于未来PageRank值的预测，基于持续关注度衰减算法要稍逊于FutureRank算法，但这种优势不是很明显。而且前面的分析已经发现，对于预测较靠前（APS数据前500名，arXiv数据前50名）的论文的情况下（见2.3.2.1节），基于持续关注度衰减算法预测未来PageRank值排序的准确率要优于FutureRank算法。这种差异性出现的根本原因是基于持续关注度衰减算法本身是基于论文的引用次数计算的，而FutureRank算法是基于论文的PageRank值计算的。

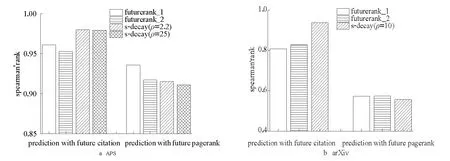
图8 算法spearman秩相关系数比较Fig.8 Comparision of the spearman’s rank correlation

表3和表4分别给出了基于持续关注度衰减算法在两个数据集上得到的前20篇论文（表中第1列）与真实排名比较情况。从表3可以看到比较显著的是编号为“199908142”的论文，2000年之前它的排名为222，未来的排名跃居为第2，而算法能将它预测进前20。此外，论文“199905111”之前为81名，2000年之后排名第6，算法较准确地预测出其潜在价值。

而在 APS数据集上（见表4），比较显著的是论文10.1103／PhysRevLett.77.3865，10.1103／PhysRevB.54.11169，10.1103／PhysRevB.37.785，10.1103／PhysRevLett.80.149和论文10.1103／PhysRevB.37.785，这类论文在2000年以前排名比较靠后，但是未来排名靠前，属于潜在价值比较大的文献，算法能较准确地将其挖掘出来。

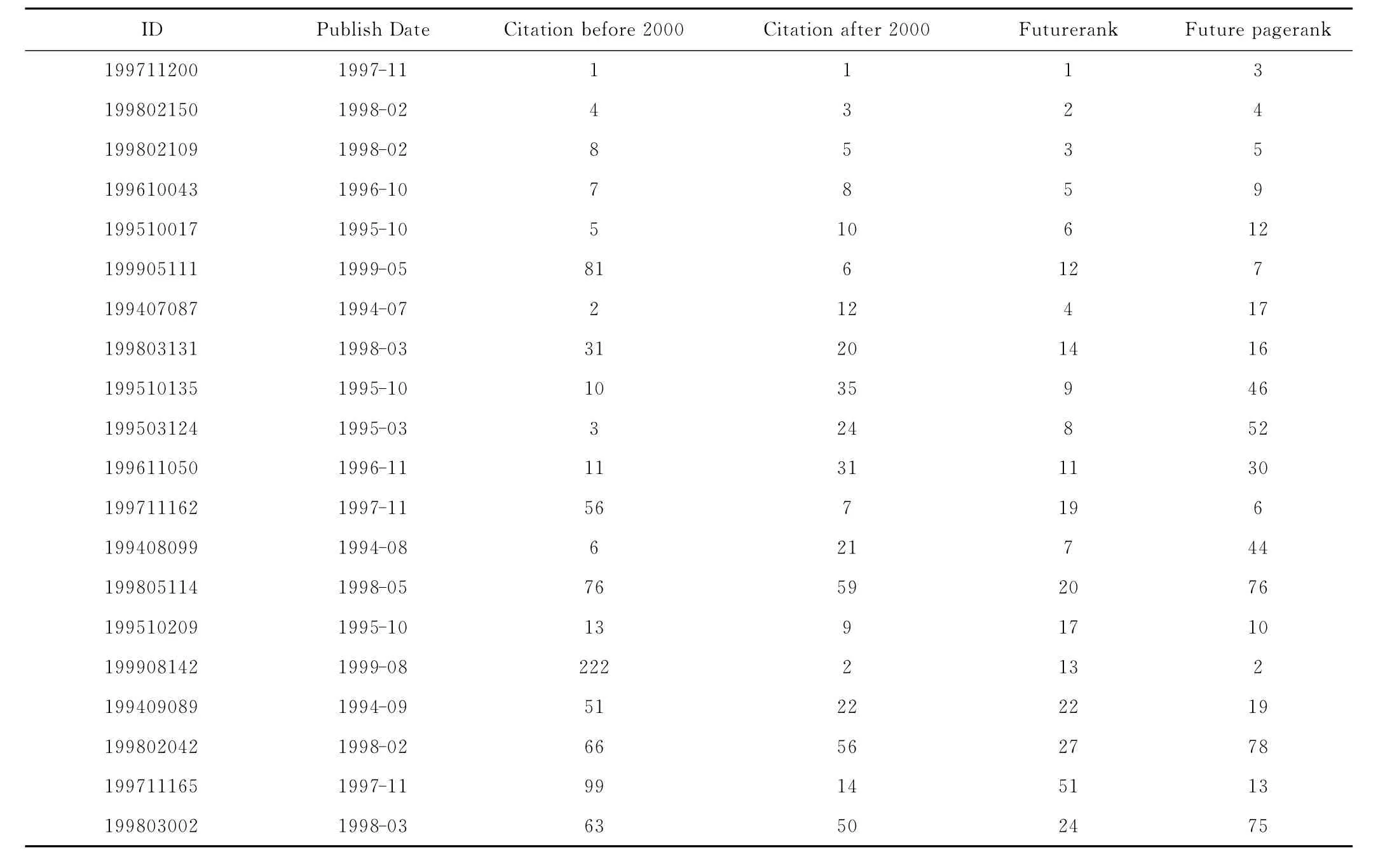
表3 arXiv数据集预测排名前20位与真实排名比较Tab.3 Comparison of the predicted rank and the real rank of the Top20for arXiv data set

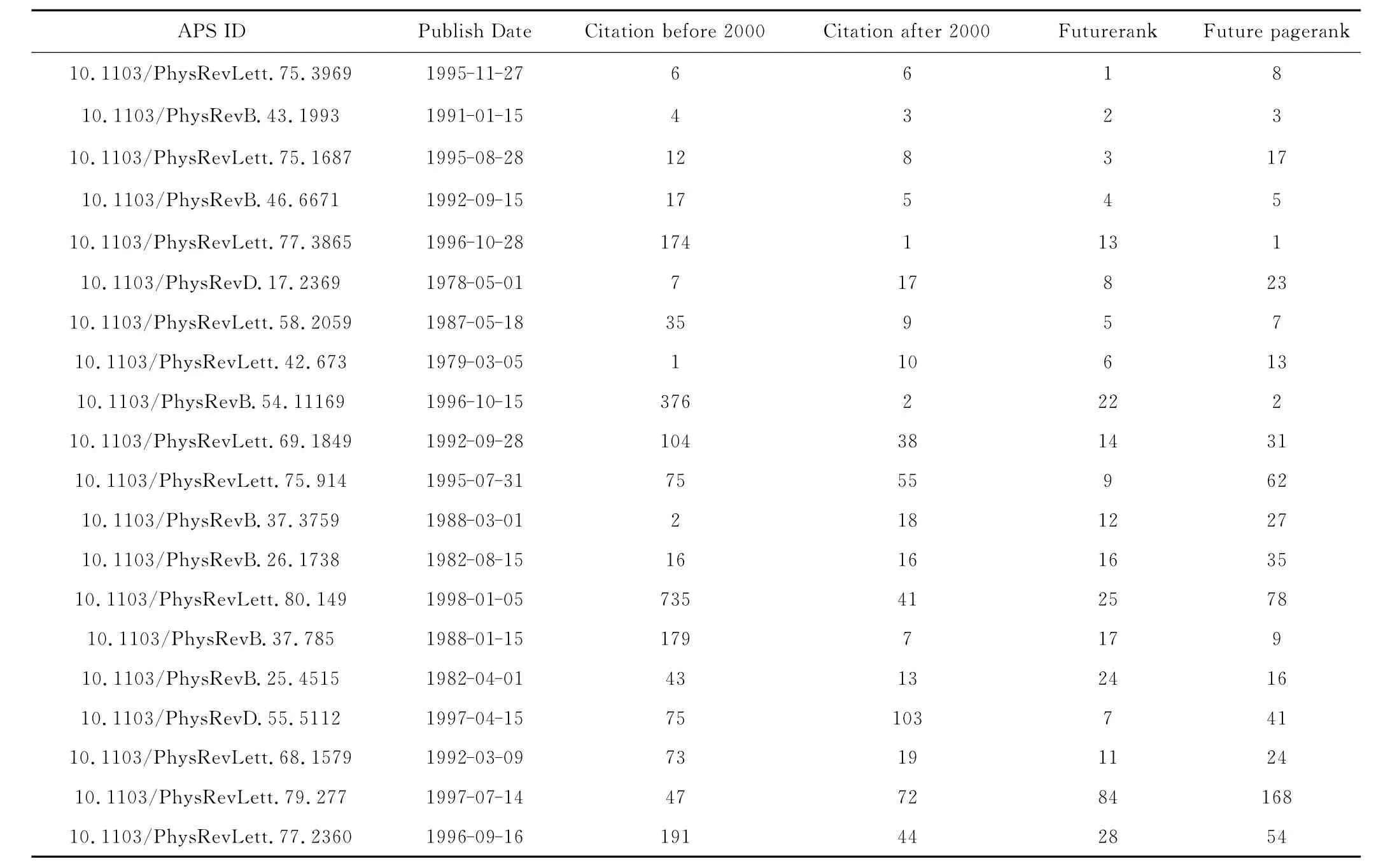
表4 APS预测前20名与真实排名比较Tab.4 Comparison of the predicted rank and the real rank of the Top20for APS data set

3 总结和讨论

本文提出一种基于持续关注度衰减的重要论文预测算法（s－decay），该方法的优点有：1）预测准确性较高。对于预测排名靠前的论文未来被引情况，本文算法精确率高于FutureRank算法以及z－score值预测算法，只是预测PageRank值排序的全局相关度要稍逊于FutureRank算法；2）本文算法仅含有一个时间参数，且对参数不敏感；3）本文算法不需要处理作者等文本信息，仅仅依据论文随时间变化的关注度进行论文价值预测，对数据要求低，计算复杂度较低，适用于大规模数据集的处理；4）本文算法在两个不同的数据集上表现效果也较稳定。

本文综合考虑论文被引趋势呈现负指数衰减的特性和论文持续关注度蕴含论文被引潜力的特性，提出基于持续关注度衰减的算法。该算法能较好地预测论文的未来被引排名，但由于算法通过论文过去一段时间的被引用情况来判断其是否具有继续被关注的潜力，所以论文必须有被引用的记录，才能加以判断。对一些刚刚发表的论文，由于没有引用链接或者过少，对其的预测准确性会大大降低。为此我们猜想是否可将论文所发表的期刊信息，论文所属的研究领域等因素来预测论文未来的被引情况。此外，被引文献来自于多个领域，从属多个类型的论文和引文领域单一，类型单一的论文相比，在未来受到的关注将会更多，被引用潜力也相对更大，论文引文的“多样性”也可作为研究论文潜在价值的重要依据。

［1］ Wang D，Song C，Barabási A L.Quantifying long－term scientific impact［J］.Science，2013，342（6154）：127－132.

［2］ Hirsch J E.An index to quantify an individual＇s scientific research output［J］.Proceedings of the National academy of Sciences of the United States of America，2005，102（46）：16569－16572.

［3］ Egghe L.Theory and practise of the g－index［J］.Scientometrics，2006，69（1）：131－152.

［4］ Ding Y，Yan E，Frazho A，et al.PageRank for ranking authors in co－citation networks［J］.Journal of the American Society for Information Science and Technology，2009，60（11）：2229－2243.

［5］ Liu X，Bollen J，Nelson M L，et al.Co－authorship networks in the digital library research community［J］.Information Processing ＆ Management，2005，41（6）：1462－1480.

［6］ Medo M，Cimini G，Gualdi S.Temporal effects in the growth of networks［J］.Physical Review Letters，2011，107（23）：238701.

［7］ Berberich K，Vazirgiannis M，Weikum G.Time－aware authority ranking［J］.Internet Mathematics，2005，2（3）：301－332.

［8］ Walker D，Xie H，Yan K K，et al.Ranking scientific publications using a model of network traffic［J］.Journal of Statistical Mechanics：Theory and Experiment，2007，2007（06）：P06010.

［9］Zhou Y B，LüL，Li M.Quantifying the influence of scientists and their publications：distinguishing between prestige and popularity［J］.New Journal of Physics，2012，14（3）：033033.

［10］Yan E，Ding Y，Sugimoto C R.P－Rank：an indicator measuring prestige in heterogeneous scholarly networks［J］.Journal of the American Society for Information Science and Technology，2011，62（3）：467－477.

［11］Zhou D，Orshanskiy S A，Zha H，et al.Co－ranking authors and documents in a heterogeneous network［J］.IEEE International Conference on Data Mining，2007，739－744.

［12］Kleinberg J M.Authoritative sources in a hyperlinked environment［J］.Journal of the ACM （JACM），1999，46（5）：604－632.

［13］Shen H，Wang D，Song C，et al.Modeling and predicting popularity dynamics via reinforced poisson processes［J］.Eprint arXiv，2014：arXiv：1401.0778.

［14］Yan E，Ding Y.Weighted citation：an indicator of an article＇s prestige［J］.Journal of the American Society for Information Science and Technology，2010，61（8）：1635－1643.

［15］Sayyadi H，Getoor L.FutureRank：ranking scientific articles by predicting their future pagerank［J］.Proc of Siam International Conference on Data Mining，2009：533－544.

［16］Page L，Brin S，Motwani R，et al.The pageRank citation ranking：bringing order to the web［J］.Lecture Notes in Engineering，1998，9（1）：1－14.

［17］Radicchi F，Fortunato S，Vespignani A.Citation networks［J］.Understanding Complex Systems，2012：233－257.

［18］Wu Z X，Holme P.Modeling scientific－citation patterns and other triangle－rich acyclic networks［J］.Physicl Review E，2009，80（3）：037101.

［19］Newman M E J.Prediction of highly cited papers［J］.Earophysics Letters，2014，105（2）：28002－28007.

［20］Newman M E J.The first－mover advantage in scientific publication［J］.Europhysics Letters，2009，86（6）：68001.