不确定复杂网络的广义矩阵投影同步

巩长忠，李飞燕

（中国民航大学理学院，天津300300）

0 引言

复杂网络在自然界中普遍存在，例如，交通运输网络、万维网（WWW）、生态网络、新陈代谢网、人际关系网络等等。因此，它在我们的日常生活中已经变得越来越重要。复杂网络的本质就是复杂性，包括网络的拓扑结构、动力学演化、节点多样性等等。最近由于计算机的快速发展，我们能够快速处理网络中的大规模数据。随着“小世界网络”和“无标度网络”［1－2］诞生，复杂网络的研究已经成为一个热点，吸引了许多科学和工程领域人士的关注。

在许多复杂动力学行为中，网络同步是一个非常有意义的现象，已经成为复杂网络研究的一个焦点。自从Pecora［3］提出并率先实现混沌同步以来，许多同步的方法（完全同步［4］、相同步［5］、滞后同步［6］、广义同步［7］、投影同步［8－9］）先后被学者提出，投影同步是由Mainieri和Rehacek在研究部分线性混沌系统时首次提出的［10］。它由于其比例特性能够使得混沌通信更加安全，所以广义投影同步近年来得到广泛的研究［11－13］。最近，文献［14］研究了一类参数未知的超混沌系统的广义函数投影滞后同步。文献［15］研究了两个不同的复杂网络间的广义矩阵投影滞后同步。网络的节点可以有不同的动力学行为并且网络维数也可以不同，研究结果不适用于参数不确定或者拓扑结构未知的复杂网络。但现实的复杂网络中存在着如节点的动力学系统含有未知参数或者网络结构只是部分已知或者完全未知［16－18］。文献［19］研究了带有自适应双尺度函数的不确定复杂网络的自适应同步，并且未知的拓扑结构及未知参数可以识别，但没有考虑时滞。在实际应用中复杂网络节点间不仅存在t时刻的信息通信，而且也存在t－τ（t）时刻的信息通信［20－21］，即系统的演化趋势不仅依赖于系统当前的状态，也依赖于系统过去某一时刻的状态。文献［22］研究了复杂网络的线性广义同步。从以上研究成果中可以看出，在已有的大部分不确定复杂网络的研究中，网络模型维数都是相同的并且拓扑结构也相同，当网络的拓扑结构不同或维数不相等时，以往的方法就受到了限制难以适用。例如同步将通过不同维数的振荡器来实施，特别是生物科学和社会科学系统。

本文研究节点不恒等且维数不同的变时滞、不确定复杂网络的广义矩阵投影同步，它不仅仅使得不确定复杂的模型更加一般化，而且使得投影同步由一个常数或者对角矩阵演变为一个广义矩阵，基于Lyapunov稳定性理论，利用自适应控制器得到了不确定复杂网络广义矩阵投影同步的判别准则，另外给出了一种响应网络的构造方法，这种方法适应于几乎所有的不确定复杂网络。数值模拟结果验证了方法的有效性和可行性。

1 网络模型和预备知识

1.1 网络模型

考虑一类含有N个非恒等节点，带有时滞耦合的不确定复杂网络：

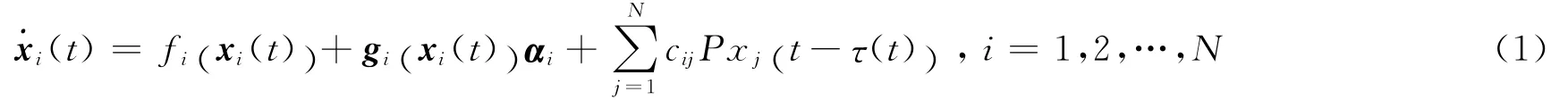
其中，xi（t）＝ （xi1，xi2，…，xin）T∈Rn是第i个节点的状态变量；fi：Rn→Rn与gi：Rn→Rn×l是连续的非线性可微函数；τ（t）为节点间的时滞函数；αi∈Rl为l维未知参数；P∈Rn×n是内部耦合矩阵；C＝ （ciij）N×N∈RN×N是代表网络耦合强度和拓扑结构的配置矩阵。矩阵C定义为：若第i个节点与第j个节点之间有连接（i≠j），则中每一行元素和为零，记方程 （1）为驱动网络。

把含有非线性控制器的时滞耦合网络记为响应网络，其形式如式（2）：

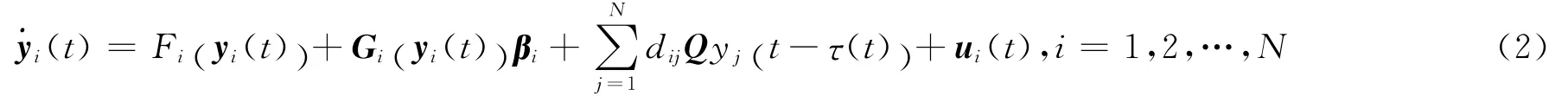
其中，yi（t）＝ （yi1，yi2，…，yim）T∈Rm是第i个节点的状态变量；Fi：Rm→Rm与Gi：Rm→Rm×r是连续的非线性可微函数；τ（t）为节点间的时滞函数；βi∈Rr为r维未知参数；ui（t）∈Rm是自适应控制器；Q∈Rm×m是内部耦合合矩阵；D＝ （diij）N×N∈RN×N是代表网络的耦合强度和拓扑结构的配置矩阵，与矩阵C有相同的定义。

1.2 预备知识

定义1 设xi（t）是驱动网络（1）中第i个节点的当前状态变量，yi（t）是响应网络（2）中第i个节点的当前状态变量。对于xi（t），yi（t）如果存在一个常数矩阵M ∈Rm×n，并且 ‖M‖ ≠0，使得

那么当τ（t）＞0时，网络 （1），（2）达到广义矩阵投影同步（GMPS）。

引理1 任给x，y∈Rn以及正定矩阵S，有2xTy≤xTSx＋yTS－1y 。假设1 存在非负常数l1，l2，使得对于任给定的x，y∈Rn有：

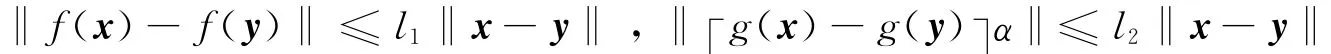
假设2 假设存在时滞函数τ（t）（＞0）是可微的，并且˙τ（t）≤η＜1，η是正常数。

2 同步准则

定义同步误差：

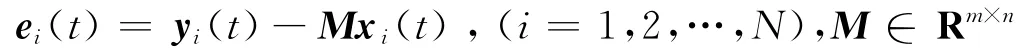
对时间t求导：

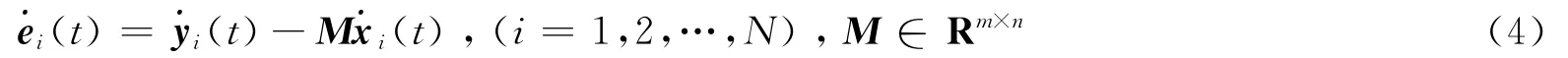
将方程 （1），（2）代入 （4）中，得到误差的动力学系统为

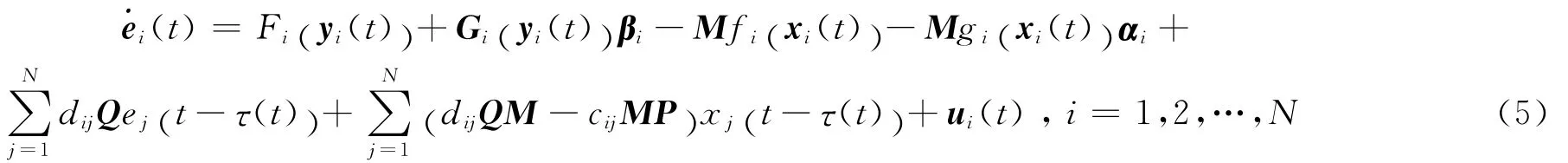
因此，当t→ ∞ ，ei（t）→0，网络 （1），（2）实现了GMPS，则网络 （1），（2）的广义矩阵投影同步的实现就转化为使误差ei（t）零解的渐近稳定问题。

定理1 对于给定的广义矩阵M ∈Rm×n（‖M‖≠0），在如下控制器和适应律作用下，网络 （1），（2）实现了GMPS，并且未知的参数可以辨识，即

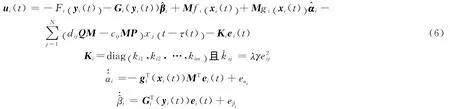
将（6）式代入（5）中，同步误差动力学系统将被描述为

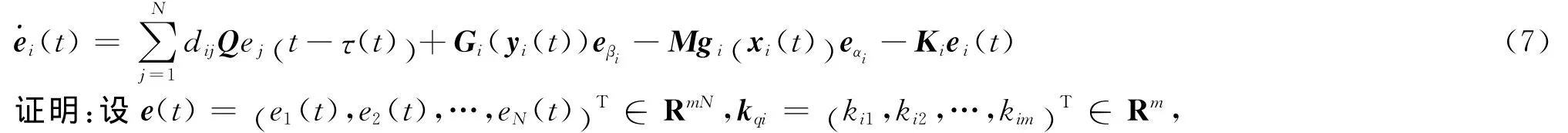
Iq＝ （1，1，…，1）∈Rm，I∈Rm×m是恒等矩阵。

构造李雅普诺夫函数：

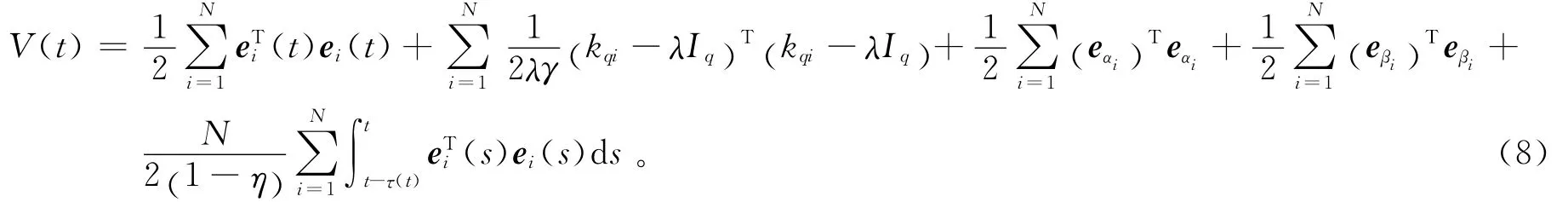
显然V（t）≥0，即V（t）为正定函数，V（t）关于t求导：

利用引理1，由于

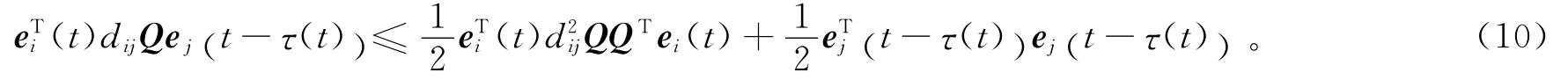
于是，将 （10）代入 （9）中

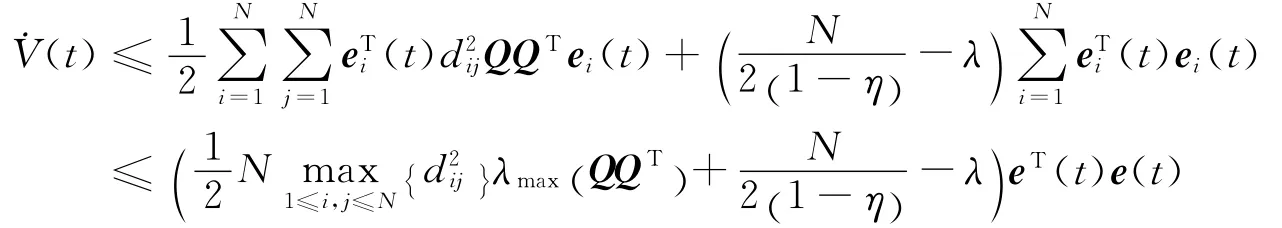
若令

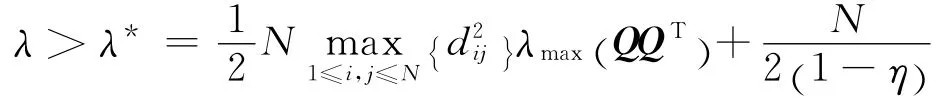
λmax（QQT）为矩阵ATA 的最大特征值，故（t）≤－eT（t）e（t），当（t）＝0时，ei（t）→0；当˙V（t）＜0时，由Lyapunov稳定性定理可得误差ei（t）的零解是渐近稳定的，故网络（1），（2）实现了GMPS。由定理1中的控制器和自适应律（6）可知未知参数可以辨识，即

如果MTM是可逆的，并且驱动网络（1）中的耦合系数及节点参数都未知的情况下，构造如式（11）响应网络，使其与未知的驱动网络（1）对于给定的常值矩阵M实现GMPS。

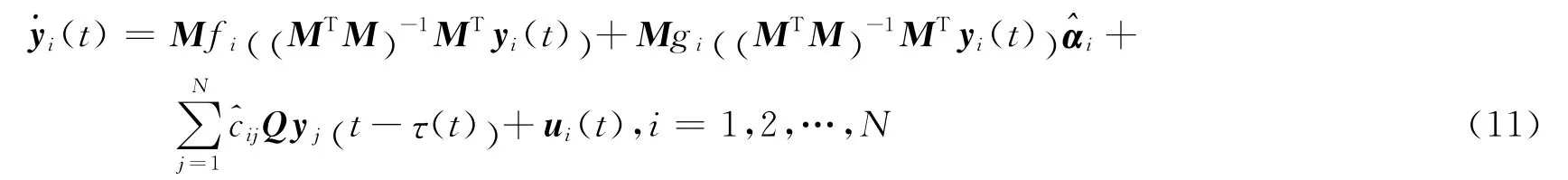
定义网络 （1）和 （11）同步误差：ei（t）＝yi（t）－Mxi（t），（i＝1，2…，N），M ∈Rm×n，对时间t求导，并将方程 （1），（11）代入得到误差的动力学系统：

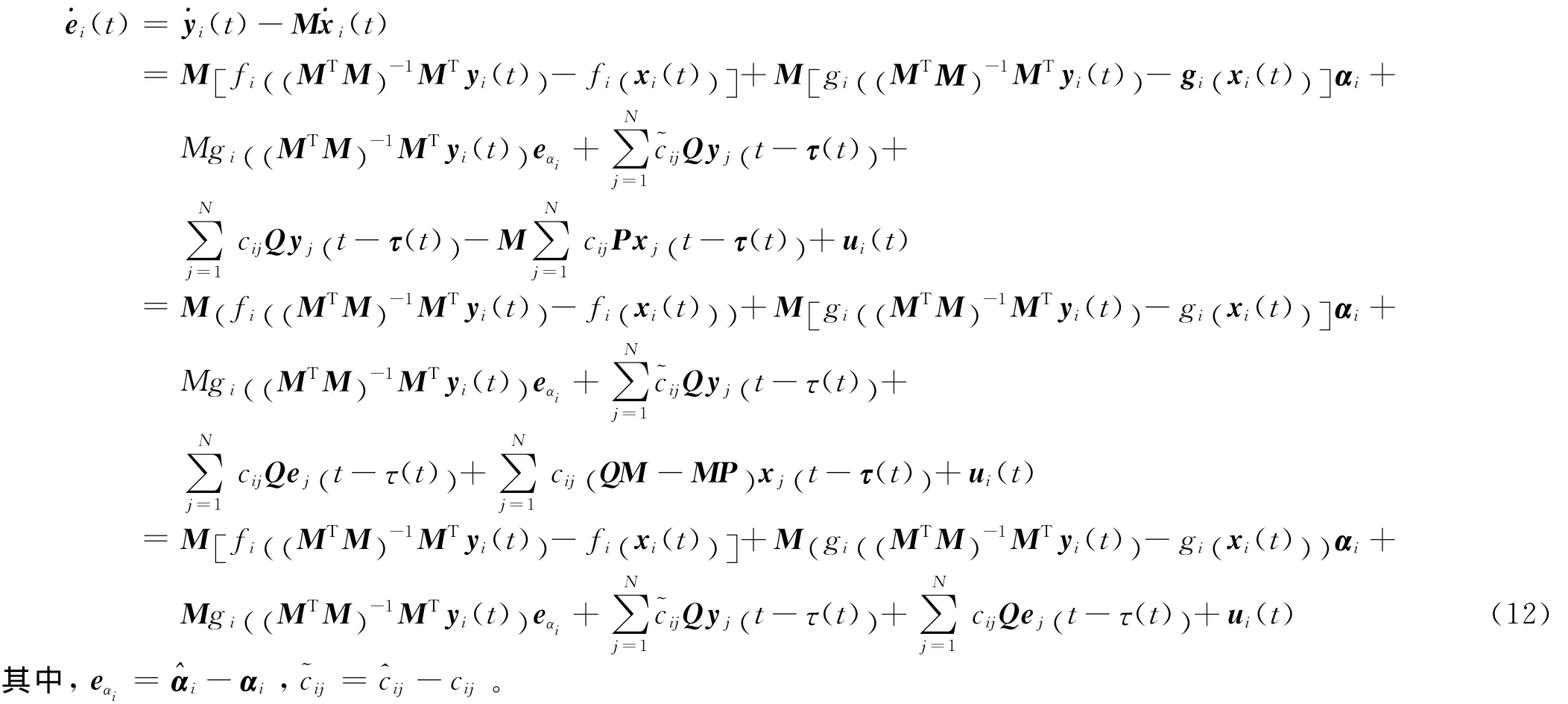
因此，若t→ ∞ 时，ei（t）→0，就说网络 （1），（11）达到了广义矩阵投影同步，即响应系统 （11）构造成立，于是（1），（11）的广义矩阵投影同步的实现就转化为使误差ei（t）零解的渐近稳定问题。

定理2 在假设（1），（2）成立的情况下，对于给定的常数尺度矩阵M∈Rm×n（‖MTM‖≠0），在以下控制器和自适应律作用下，（1），（11）达到了广义矩阵投影同步，并且未知的参数可以辨识。即

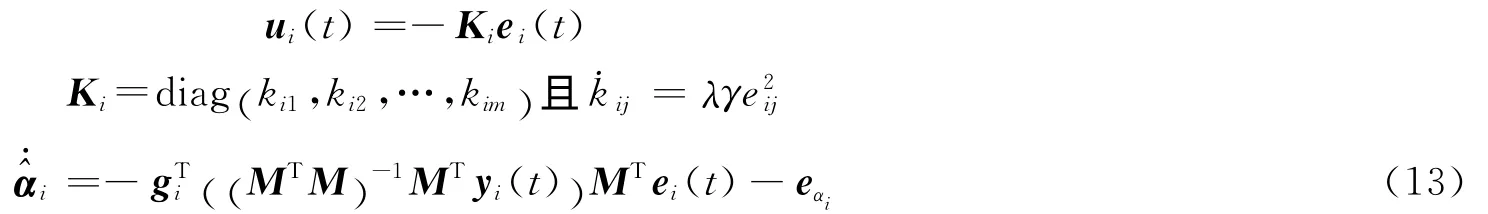
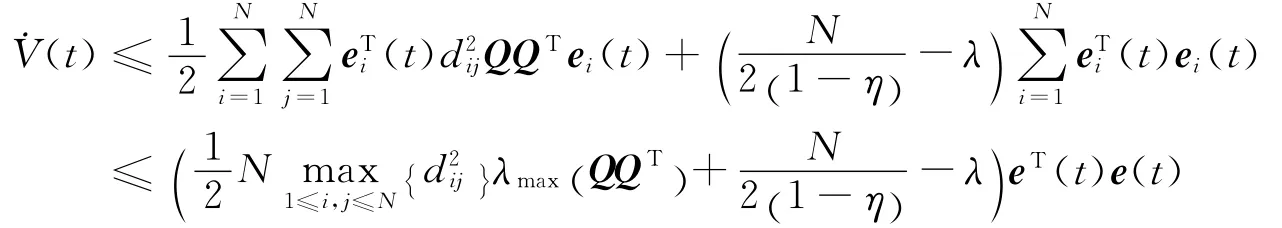
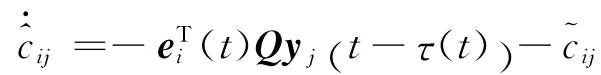
其中，i＝1，2，…N，j＝1，2，…，m 。

证明：考虑以下李雅普诺夫函数

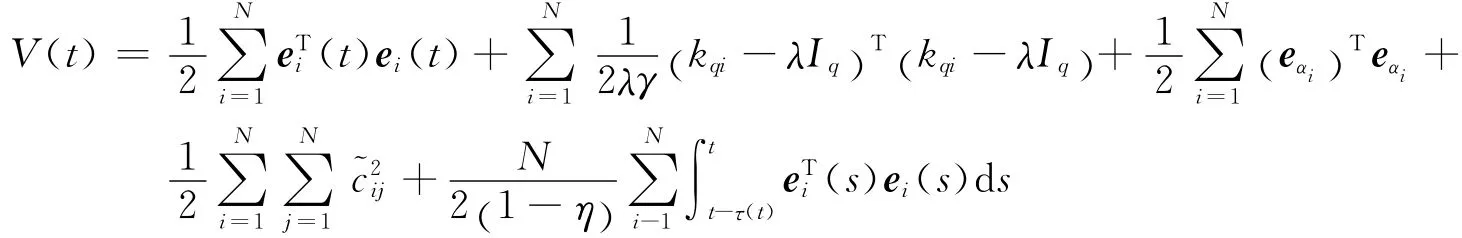
显然V（t）≥0，即V（t）为正定函数，V（t）关于t求导：

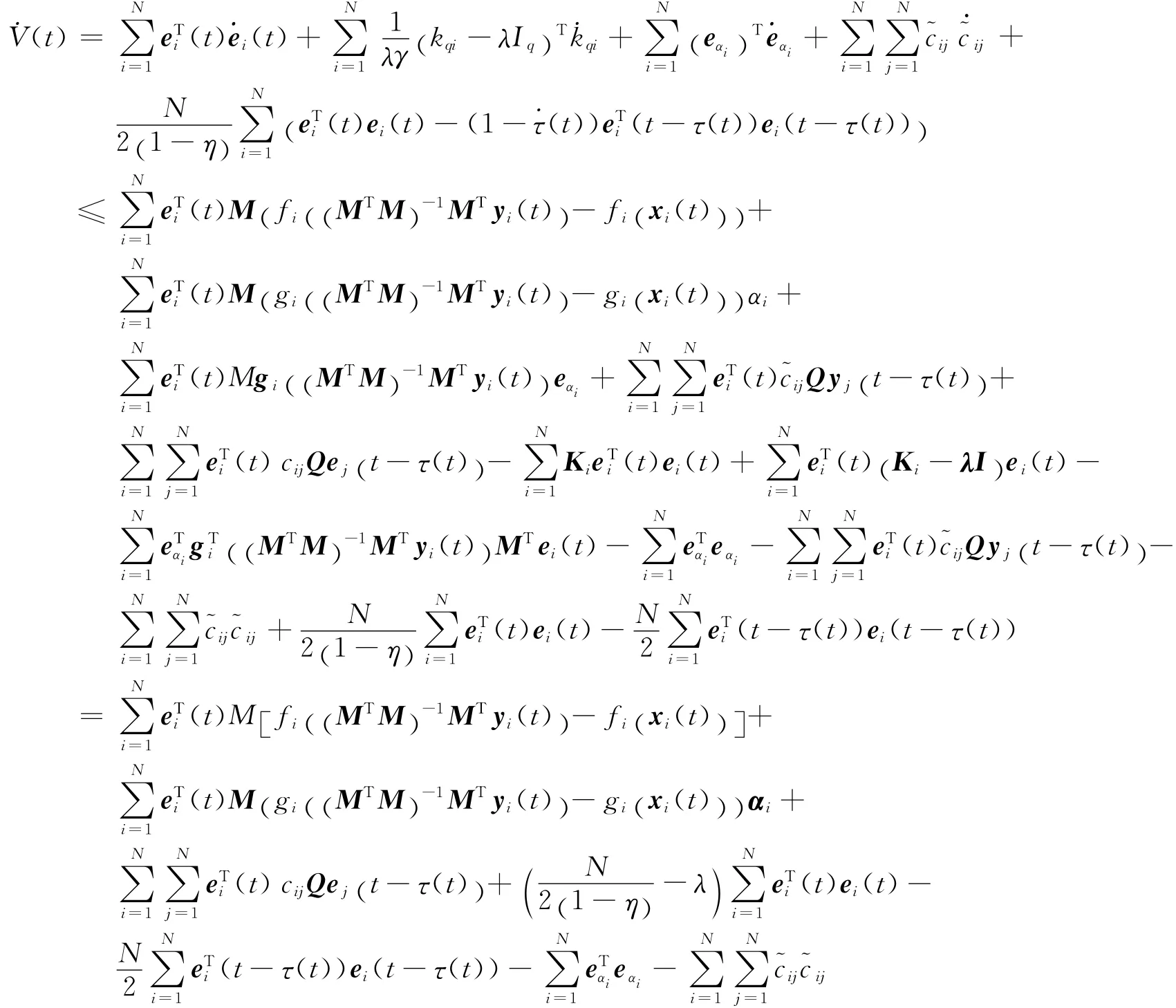
由假设（2）可知及引理（1）可知

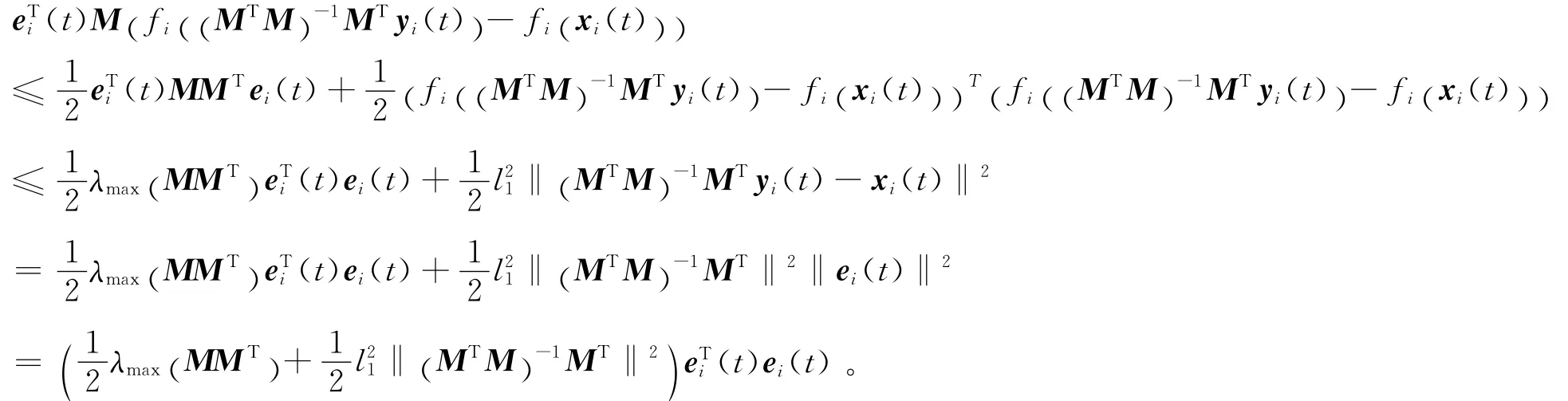
同理

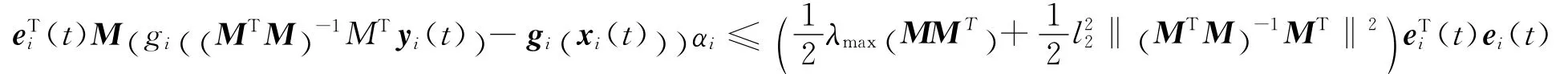
利用 （10）式得

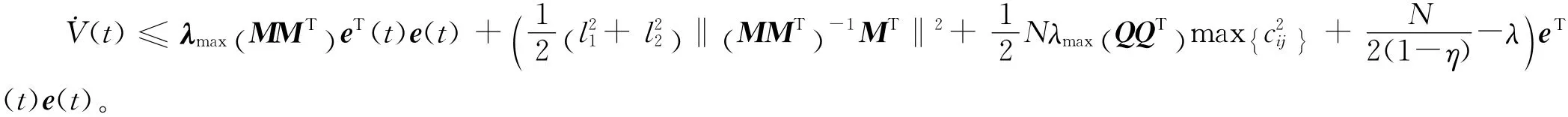
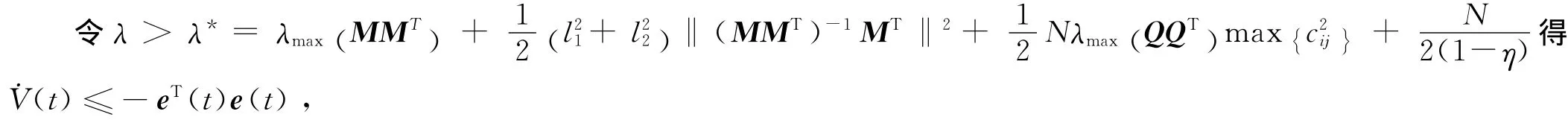
3 数值仿真

下面以Lorenz混沌系统和超混沌Lü系统为例，验证理论的正确性和有效性。

选取N个不同的三维Lorenz混沌系统描述如式（14）：

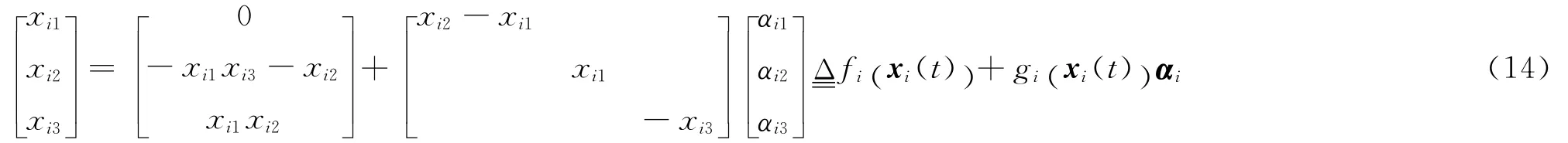
其中，xi1，xi2，xi3为第i个系统的状态变量，αi1，αi2，αi3为系统的未知参数，当时，系统式（14）处于混沌状态。

选取N个不同的四维超混沌Lü系统描述如式（15）：

其中，yi1，yi2，yi3，yi4为第i个系统的状态变量，βi1，βi2，βi3，βi4为系统的未知参数。当βi1＝10，βi2＝5，βi3＝3，βi4＝0．5时，系统式（15）处于超混沌状态。

为了仿真的方便，取含有5个节点的网络进行仿真，由于网络的配置矩阵是任意的，所以不妨取星形网络和全局耦合网络的配置矩阵C和D为

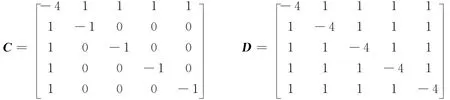
取系统内部耦合矩阵为恒等矩阵，即P∈I3×3，Q∈I4×4，时滞函数

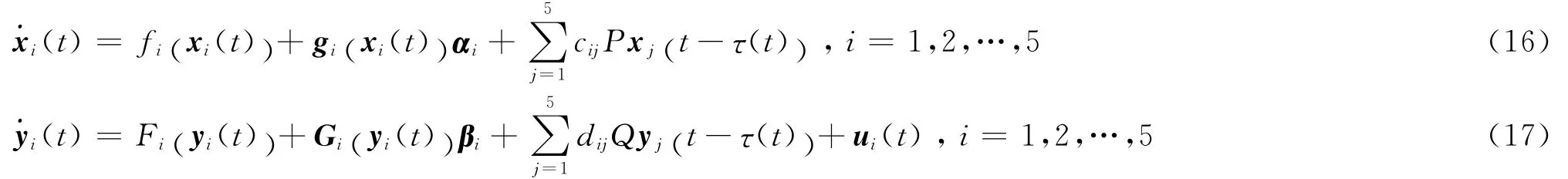
例1 使用（16）为驱动网络，（17）为响应网络，由定理1中证明过程可知λ＊≈42．8，取λ＝100，γ＝0．1，尺度，采用定理1中的控制器，未知参数估计值的初始值以及网络（16），（17）的初始值在（0，1）之间任意取。

仿真结果如图1所示，图1给出了误差曲线，可以得出复杂网络（16），（17）在定理1控制器的作用下，趋于矩阵投影同步；图2、图3分别给出了参数αi，βi的估计，随时间变化的曲线图，可以看出网络中所有的未知参数都收敛到真值。

图1 误差曲线Fig.1 The error curve

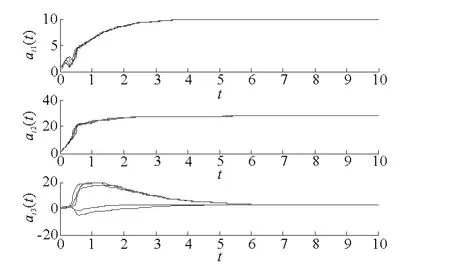
图2 参数αi的估计Fig.2 The estimation ofαi

例2 使用（16）作为驱动网络，参数αi与耦合矩阵C未知，构造式（18）网络作为响应网络

其中，

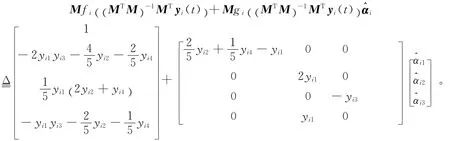
取Q∈I4×4，的初值在（0，1）之间任意取，常值矩阵M 及其余一切初值的取法同例1，采用定理2中的控制器，图4给出了误差曲线，可以看出（16），（18）在定理2中控制器的作用下趋于GMPS，图5给出了参数αi的估计αi随时间变化的曲线图；图6给出了网络的拓扑结构cij的估计随时间变化的曲线，可以看出网络中所有的未知参数都收敛到真值。

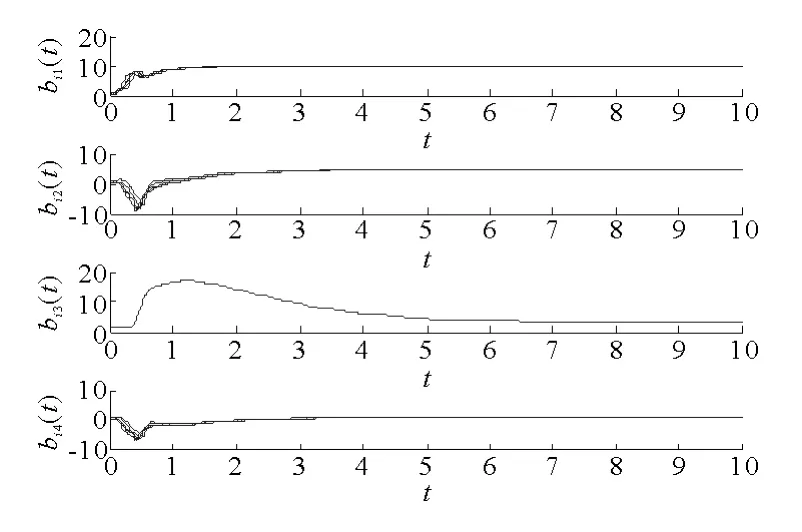
图3 参数βi的估计Fig.3 The estimation ofβi

图4 误差曲线Fig.4 The error curve

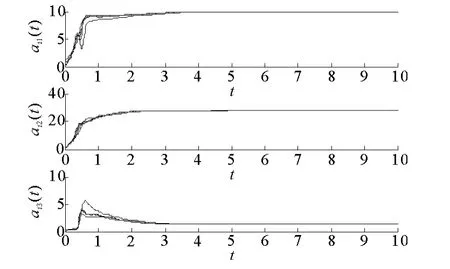
图5 参数αi的估计Fig.5 The estimation ofαi

图6 网络的拓扑结构 的估计Fig.6 The estimated toloplogy

4 结语

本文采用自适应控制的方法研究了变时滞耦合的两个不确定复杂网络的广义矩阵投影同步。每个网络的维数不同、拓扑结构不恒等且节点带有不同的动力学。一方面，基于Lyapunov稳定性理论，在节点参数未知的情况下，给出了不确定复杂网络广义矩阵投影同步的充分条件，参数可以识别；另一方面，当驱动网络中的耦合系数也未知时，可以构造响应网络，对于给定的广义矩阵使其与驱动网络达到投影同步，未知参数可以辨识，这不仅可以对该网络进行同步控制达到预期效果，而且可以对参数进行辨识，确定网络结构。最后数值仿真验证了方法的有效性和可行性。现有与此类似的研究主要有如下两个方面的工作：1）节点不恒等并且维数不同的复杂网络自适应同步模型，其网络耦合项无时滞且节点参数已知；2）复杂网络的动力学节点含未知参数，而网络的维数相同且耦合项为时滞而非变时滞的同步模型。该同步模型对结点含未知参数、耦合时滞且维数相同的复杂网络同步的情况进行了推广，具有更广的适用范围。

［1］ Watts D J，Stogatz S H.Collective dynamics of＇small－world＇networks［J］.Nature，1998，393（6684）：440－442.

［2］ Barabasi A L，Albert R .Emergence of Scaling in Random Networks［J］.Science，1998，286（5439）：509－520.

［3］ Pecora L M，Carroll T L.Synchronization in chaotic system ［J］.Physical Review Letters，1990，64（8）：821－824.

［4］ Agiza H N.Chaos synchronization of Lüdynamical system ［J］.Nonlinear Analysis，2004，58（1／2）：11－20.

［5］ Pikovsky A S，Rosenblum M G，Osipov G V.Phase synchronization of chaotic oscillators by external driving［J］.Physica D：Nonlinear Phenomena，1997，104（3／4）：219－238.

［6］ Li C D.Liao X F，Wong K W.Chaotic lag synchronization of coupled time－delayed systems and its applications in secure communication［J］.Physica D：Nonlinear Phenomen，2004，194（3／4）：187－202.

［7］ Rulkov N F.Sushchik M M，Tsimring L S，et al.Gneralized synchronization of chaos in directionally coupled chaotic systems［J］.Phys Rev E，1995，51（4）：980－994.

［8］ Yan J P，Li C P.Generalized projective synchronization of a unified chaotic system［J］.Chaos Solitons and Fractals，2005，26（4）：1119－1124.

［9］ Li G H.Modified projective synchronization of chaotic system ［J］.Chaos Solitons and Fractals，2007，32（5）：1786－1790.

［10］Mainieri R，Rehacek J.Projective synchronization in three－dimensional chaotic systems［J］.Physical Review letters，1999，82（15）：3042－3045.

［11］Li C P，Yan J P.Generalized projective synchronization of chaos：The cascade synchronization approach［J］.Chaos Solitons and Fractals，2006，30（1）：140－146.

［12］Li G H.Generalized projective synchronization of two chaotic systems by using active control［J］.Chaos Solitons and Fractals，2006，30（1）：77－82.

［13］Li Z G，Xu D L.Stability criterion for projective synchronization in three－dimensional chaotic systems［J］.Phys Letter A，2001，282（3）：175－179.

［14］柴秀丽，武相军.一类参数未知超混沌系统的广义函数投影滞后同步［J］.计算机应用，2013，33（3）：734－738.Cai Xiuli，Wu Xiangjun，Generalized function projective lag synchronization of a class of hyperchaotic systems with fully uncertain parameters［J］.Journal of Computer Applications，2013，33（3）：734－738.

［15］Dai H.Jia L X.Zhang Y B.Adaptive generalized matrix projective lag synchronization between two different complex networks with non－identical nodes and different dimensions［J］.Chin Phys B，2012，21（12）：141－152.

［16］Zhou J，Lu J A.Topology identification of weighted complex dynamical network［J］.Physica A，2007，386（1）：481－491.

［17］Li K，Lai C H，Adaptive－impulsive synchronization of uncertain complex dynamical networks［J］.Physics Letters A，2008，372（10）：1601－1606.

［18］Xu Y H，Zhou W N，Fang J A，et al.Topology identification and adaptive synchronization of uncertain complex networks with non－derivative and derivative coupling［J］.Journal of the Franklin Institute，2010，347（8）：1566－1576.

［19］Xu Y H.Zhou W N.Fang J A.Sun W.Topology identification and adaptive synchronization of uncertain complex networks with adaptive double scaling functions［J］.Common Nonlinear Sci Numer Simulat，2011，16（8）：3337－3343.

［20］Wu X J，Lu H.Generalized function projective（lag，anticipated and complete）synchronization between two different complex networks with nonidentical nodes［C］.Commun Nonlinear Sci Numer Simulat，2012，17（7）：3005－3021.

［21］李德奎，张建刚.时滞和非时滞耦合的驱动响应动态网络的函数投影同步［J］.太原理工大学学报，2013，44（2）：162－167.Li Dekui，Zhang Jiangang.Function projection synchronization of drive－response dynamical networks with non－delayed and delayed coupling［J］.Journal of Taiyuan University of Technology，2013，44（2）：162－167.

［22］卞秋香，姚洪兴.复杂网络的线性广义同步［J］.系统工程理论与实践，2011，31（7）：1334－1340.Bain Qiuxiang，Yao Hongxing.Linear generalized synchronization of complex networks［J］.Systems Engineering－Theory and Practice，2011，31（7）：1334－1340.