多重网络的结构与鲁棒性

李 明，汪秉宏

（中国科学技术大学近代物理系，合肥230026）

0 前言

当今社会中，无论是科学研究，还是日常生活，“网络”都是出现频率很高的词汇之一，如量子网络、网络计算、网络聊天、网络游戏、网络教育、网络购物、网络营销等。可以说，当今社会就是一个网络的社会。

一般地，一个由多个体组成的相互作用系统都可以用网络描述［1－2］。由于网络的表示形式可以突显一个系统的结构与个体间的关联性，所以利用网络的方法研究复杂系统也得到了大量的关注［1－6］。这些研究让我们对复杂系统的结构与动力学特性有了更为深刻的认识。例如，通过研究人际接触网络的特性，可以找到更为有效的控制流行病传播的方法。

随着对网络特性研究的深入，研究人员发现单一的网络结构并不能准确且充分地描述出复杂系统个体间的相互作用［7－9］。复杂系统中，个体往往会通过不同的渠道相互作用、影响。也就是说，网络中个体间会有多种连接方式。而将各种不同的连接方式混为一谈，就很可能使研究结果与真实情况出现偏差，甚至完全错误。例如，在研究流行病传播时，需要用到人际关系网络。在人际关系网络中，会有多种连接方式，如直接接触、电话、邮件、微博、微信等。在这些连接方式中，只有直接接触才会造成疾病的传播，而其它的非接触式的人际关系虽然也反映了人际关系网的连接性，但并不能传播疾病。所以，研究中区分这些不同种类的连接是很有必要的。多重网络即提供了这样的一个框架，可以将同一组元素间的不同作用方式区别对待，以进行更为准确的复杂系统研究［10－13］。

现实中的多重网络，还可以举出很多例子。例如，电力网络与相应的通信控制网络，各节点间既有电力供应关系，也有通信控制关系，是两种不同的层次［7］。这种系统往往以相依网络的形式来研究。这里有必要对相依网络与多重网络两个概念做一个简单的比较与解释。多重网络中，一组节点同时属于多个层次，在不同层次有不同的连接方式。相依网络，是多个网络通过节点间的耦合与依赖形成的系统，各个网络中拥有各自的节点。这两种网络很多情况下可以相互转化，研究中也可用类似的数学方法处理［14－17］。图1中，给出了一个多层网络的示意图。其中，左图为二重网络，在节点间有两种不同的连接方式，分别用实线与虚线表示，右图对应该二重网络的两层网络。这里所给出的只是一个简单的例子，而真实的多重网络可能会有更多的层次，且各层次的结构可能具有相关性。

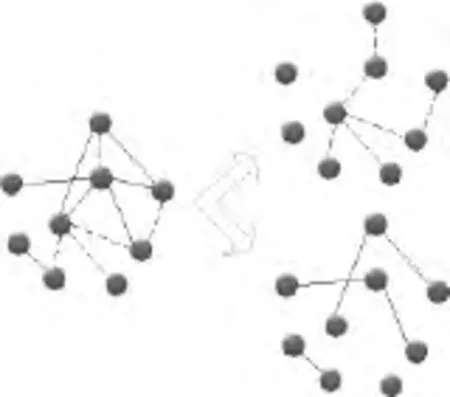
图1 多重网络示意图Fig.1 Schematic diagram of multilayer networks

1 基本概念

1.1 网络的表示

如图1所示，多重网络中只有一组节点，但有多组连边，每一组连边与节点形成一个网络，进而构成多重网络的一层。对于一个有M层的多重网络，节点i与j之间的连边情况可以用矢量aij表示：

矢量aij的维度即是网络的层数M。其中，

本文只讨论无向网络，所以aij＝aji。对于有向网络，aij与连边方向有关。另外，对于含权网络，也可令aij取其它值以表示边权，参见综述性文章［17］。

进一步，一个多重网络的邻接矩阵A可以表示为

其中，N为网络的总节点数。注意，这里的每个矩阵元都是一个M维的矢量，所以多重网络的邻接矩阵将是N×N×M的三维矩阵。

对于任意节点，在不同网络层中的度一般不同，也可以用矢量ki表示

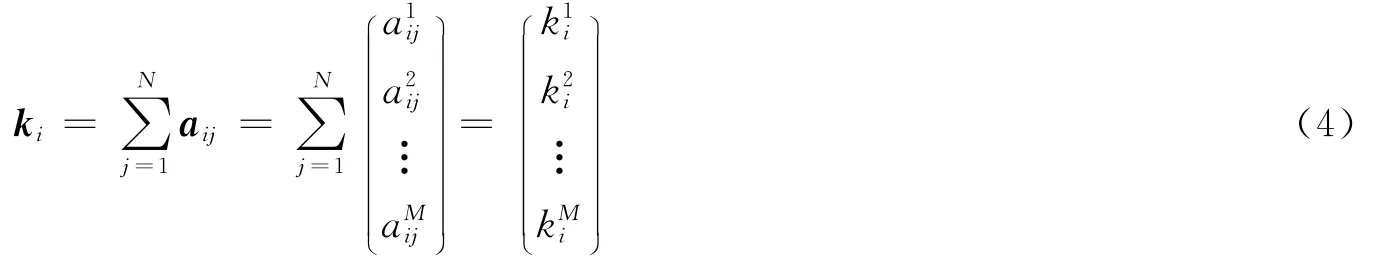
该式表示，一个二重网络中任取一个节点，它在第1层网络中度为k，在第2层网络中度为k′的概率。对于聚类系数、网络直径等参量，可以参照单个网络的定义［17］。

1.2 各层网络的关联性

真实多重网络的各层结构并不是完全独立的，而是具有一定的关联性。例如，微博网络中的大度节点在微信网络中也常常是大度节点。所以，多重网络的各层网络度分布并不相互独立［18－20］，总度分布并不总能写成各层网络度分布之积的形式（见式（5））。以两层网络为例，一般可表示为

其中，p（k｜k′）为条件概率，即第1层网络中度为k的节点在第2层网络中度为k′的概率。

为了描述多层网络之间的关联性，可以用类似Pearson系数的方式定义多层网络之间的度关联性。以两层网络为例，网络间的度关联系数可以定义为

其中，

为归一化系数。其中，尖括号表示对网络取平均。类似于单个网络中的度关联，关联系数r也满足－1≤r≤1。r值为正表示两层网络的度正相关，即一个节点在两层网络中的度大小相当；r值为负表示两层网络的度负相关，即度差别较大；r＝0，表示两层网络的度分布相互独立。

多层网络各层间的关联性还体现在：两个节点在某一层网络中相邻，那么，在其它层中也有可能相邻。仍以双层网络为例，对于第一层网络，可以用式（10）的量来描述这种关联性。

其中，ti为在两层网络中都为节点i邻居的节点数目，为节点i在第1层网络中的度。显然，当＝0时，没有节点在两层网络中都是节点i的邻居；当＝1时，节点i在第1层网络中的所有邻居在第2层网络也都是其邻居。类似地，对于第2层，也可以定义

从另一个角度看，这种共同邻居的关联性也是网络间的连边重叠性［21－22］，即有些节点在一层网络中相连，那么，在其它层中也可能相连。这一现象在现实中也很常见，例如，两个人的微博互相关注，同时还可能是QQ好友，或者还可能两人也有邮件通讯。为了描述这种结构相似性，我们还可以定义各层网络连边的重叠率。以两个网络为例，重叠率可以定义为

其中，T为两层网络中重叠的边数，E1为第1层网络的总边数。由式（12）还可以看出：

显然，当β1＝0时，两层网络结构无关联。注意，β1＝1并不能说明两层网络结构完全相同，只是说明第2层网络包含第1层网络中的所有连边，但是第2层网络可能还有其它连边。

类似地，对于第2层网络，也可以定义重叠率，

一般地，β1≠β2。

2 网络鲁棒性

网络的鲁棒性研究一直以来都是网络科学的一个重要研究方向［23－26］。所谓鲁棒性是指系统在一定扰动下，维持其某些性能的性质。在网络科学中，这种扰动即是节点或边的删除，我们关注的性质首先就是网络的连通性。

对于单一的网络，常用逾渗模型研究网络的鲁棒性［23－27］，即在一个无限大的网络中随机删除一定比例的节点（或边），最后考察剩余节点能否组成一个与原网络大小相比拟的网络。定量研究中，一般选取剩余节点的最大连通分量与原网络的大小之比S为序参量，即原网络中一个节点属于最终巨分量的概率。显然，当剩余的节点能组成一个与原网络大小相比拟的网络时有0＜S＜1，即网络巨分量存在；反之，S＝0即表示网络巨分量不存在。设初始删除的节点占网络总节点的比例为1－p。当p较小时，即删除大量节点时，网络的巨分量显然不存在（S＝0）。随着p的增加，网络的巨分量从无到有，即序参量S从零变为非零值。序参量S首次达到非零值的点称为临界点，记为pc。一个较小的临界点pc说明网络的鲁棒性很好，能够抵御大量节点的损毁；反之，则说明网络的鲁棒性很差，少量节点的损毁就会使整个网络崩溃。

2.1 无关联多重网络

对于多重网络，也可利用逾渗模型研究网络的鲁棒性。需要说明的是，在多重网络中，一个连通集团是指在各层网络中都连通的一组节点。研究中，也是将多重网络删除部分（比例1－p）节点，然后考察网络中是否存在与原网络大小相比拟的连通集团，这个集团一般称为互连巨分量［7］。

这里，将用平均场的方法对多重网络的逾渗模型进行求解［14，27－30］。根据多重网络中连通集团的定义，序参量S与控制参量p的关系式可以写为

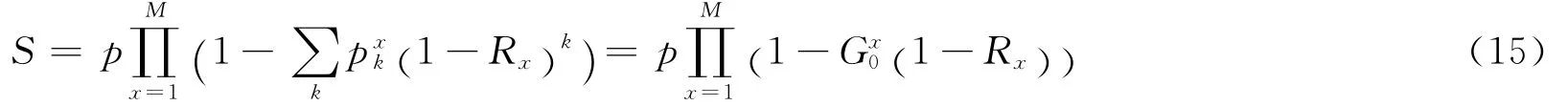
其中，Rx为第x层网络中的一条边通向互连巨分量的概率。另外

为第x层网络的度分布生成函数。式（15）的意义很容易理解即表示在第x层网络中，一个节点属于互连巨分量的概率（至少有一条边通向互连巨分量）［27］。由于考察的是无关联多重网络，这个概率相乘对各层独立，所以连乘即可得到联合概率。

类似地，还可以给出Rx所满足的方程：

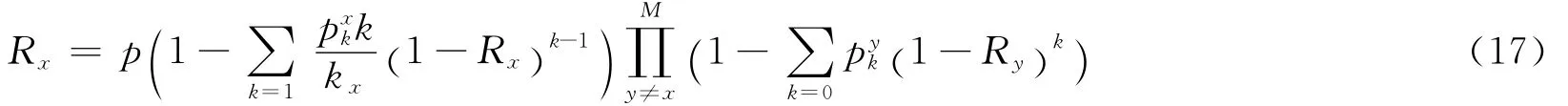
进一步，引入了第x层网络的剩余度分布的生成函数

其中，〈kx〉为第x层网络的平均度。由此，式（17）可写成更为简洁的生成函数形式

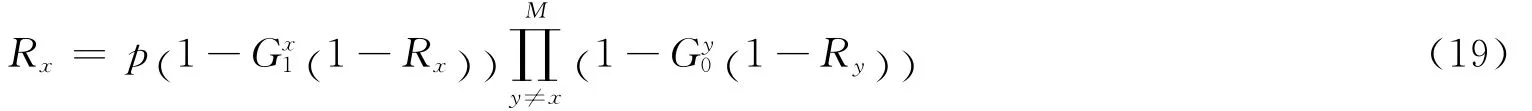
另外，注意到，当M ＝ 1时，即网络只有一层时，两个方程（15）与（19）可以退化成经典的网络逾渗方

在图2中，给出了M取不同值时，由方程（15）与（19）解出的S与p的变化关系。图中所用多重网络的每一层都是平均度为4的ER随机网络。由图可以看出，网络的层数越多，系统临界点pc越大，即网络的鲁棒性越差。这一点也很容易直观理解。因为网络层越多，在受到外部扰动时，越难保证节点在每一层网络都连通。

由图2，还可以发现，当网络只有一层时（M＝1），随着p的增加，序参量S在临界点连续变化，达到非零值，一般称为连续相变（二阶相变或更高阶）；而当网络有多层时（M＞1），序参量S在临界点跳跃式变化，一般称为不连续相变（一阶相变）。多重网络的不连续相变，也反映出多重网络的极度脆弱性与不稳定性。

对于单一网络，在外部扰动逐渐增大的过程中，网络的连通性是缓慢变化的。也就是说，实际中很容易在网络全部瘫痪前发现故障，从而避免网络的更大面积损坏。而对于多重网络，在外部扰动未达到临界点时，系统能保证很高的完整率，但是一旦到达临界点，网络就突然全部瘫痪。这种跳跃式的变化，在实际中往往使得网络故障一旦发生，整个系统就会立刻瘫痪，不留下弥补的时间。这也给实际中各种网络的保护，以及网络疾病传播的控制提出了巨大的挑战［33－36］。

2.2 关联性多重网络

2.1节对无关联多重网络的鲁棒性进行了讨论，然而真实多重网络的各层网络结构往往呈现出一定的关联性。考虑极端情况，当各层网络结构完全一样时，系统就可以退化成单一网络。由图2可知，单层网络的鲁棒性较多重网络要强很多。所以，试想当多重网络中各层之间存在一定的关联性时，即结构趋近于单一网络时，系统的鲁棒性会变得更强［18－22，37－39］。下面对这个情况的求解做一个简单的介绍。

为了方便，这里讨论一个有边重叠的二重网络［21－22］。设两层网络的边重叠率分别为β1与β2。这样，可以写出序参量S与控制参量p的关系式：

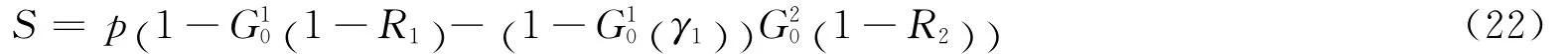
其中，G0x（z）与Rx的含义与前文相同，而γ1＝1－（1－β1）R1，γ2＝ 1－ （1－β2）R2。在式（22）中，p显然表示节点不被初始删除的概率，1－G10（1 － R1）表示节点属于第1层网络的巨分量的概率，表示节点属于第1层网络的巨分量，但不属于第2层网络的巨分量的概率。

类似地，满足

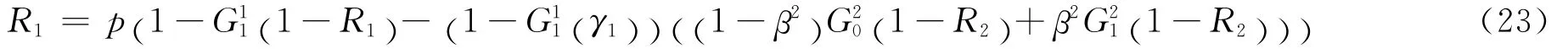
对称地，可知满足

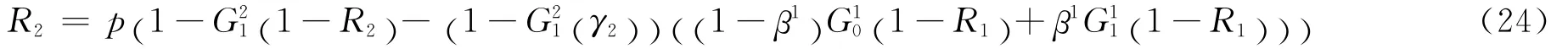
联立以上3式即可解出序参量S与p的关系，以及临界点pc。

本文给出一个具体的例子。考虑两层网络度分布相同的二重网络。这种情况下，两层网络的生成函数相同，统一记为G0（z）与G1（z）；重叠率也相同，统一记为β；R1与R2等价，统一记为R；γ1与γ2相等，统一记为γ。由此，方程（22）～（24）可简化为两个方程

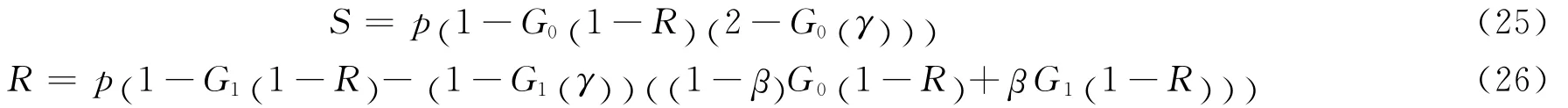
进一步，若考虑ER随机网络，则生成函数有

所以，S与R 等 价，方程（26），（27）可以合并为一个方程

在图3中，给出了式（28）相应数值解。图中给出的是网络平均度为4的ER随机网络的情况。可以看出，当重叠率较大时，系统的鲁棒性较强，而当重叠率较小时，临界点增大，即系统的鲁棒性变差。也就是说，关联多重网络要比无关联多重网络更加鲁棒。这一现象与之前我们的猜测相符。另外，我们还可以发现，在重叠率由小变大的过程中，系统的相变类型也经历了从一阶相变到二阶相变的变化。系统的临界点与三相点也可以利用式（28）得出。

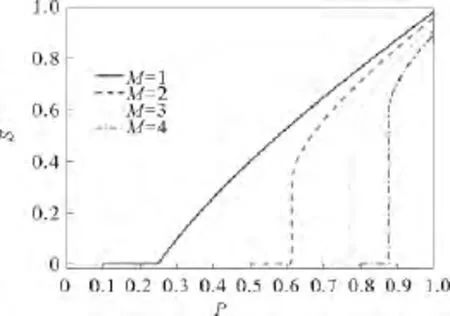
图2 多重网络的逾渗相变Fig.2 Percolation transition on multilayer networks

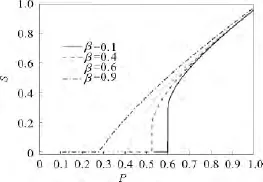
图3 关联多重网络上的逾渗相变Fig.3 Percolation transition on dependend multilayer networks

3 总结与展望

多重网络是近年来提出的一个新概念，是对过去单一的网络概念的扩展，可以更好地描述真实系统的特性。简单地说，多重网络虽然只有一组节点，但是具有多组连边，可以区分系统中不同类型的相互作用。

文中，对多重网络的概念和基本性质进行了简单的介绍，并利用生成函数计算讨论了多重网络的鲁棒性。发现相比单一网络，多重网络十分脆弱，这给实际中保护多重网络提出了巨大的挑战。同时，通过对有关联多重网络的鲁棒性的讨论，发现各层网络结构之间的关联性会使得多重网络的鲁棒性变强。各层的结构关联性越强，结构越相似，系统的鲁棒性就越强。而真实系统中各层网络的关联程度还有待进一步实证数据的统计与分析。

对于单一网络，很多网络结构特性都对网络的鲁棒性以及动力学有着重要的影响，如度分布、相配性、社团等。已有研究也表明，这些性质对多重网络的影响同样巨大，且并不与单一网络类似，甚至某些影响是相反的。例如，同配会使单一网络的鲁棒性增强［40－41］，而对于多重网络，各个层次内的同配使得网络的鲁棒性减弱［42］。

多重网络也会对网络动力学的研究带来很多新思路。如前言已经提到的信息与疾病传播的例子。虽然非接触式的人际关系对疾病传播没有直接贡献，但是也会有间接的影响。例如，通过电话、微博、微信等，疾病的信息会在人群之间传播。这种传播会使人们提前做好防护准备，以降低被感染的概率。同时，疾病信息的传播，也会使人们减少直接接触，增加其它的联系方式。也就是说，多重网络的相互作用会使得各层网络的结构发生演化［43］。然而，网络结构会怎样演化，这也是值得我们进一步研究的问题。

［1］ Dorogovtsev S N，Mendes J F F.Evolution of Networks：From Biological Nets to the Internet and WWW［M］.Oxford：Clarendon Press，2002.

［2］ Newman M E J.Networks：An introduction［M］.New York：Oxford University Press，2010.

［3］ Albert R，Barabási A L.Statistical mechanics of complex networks［J］.Rev Mod Phys，2002，74：47.

［4］ Dorogovtsev S N，Mendes J F F.Evolution of networks［J］.Adv Phys，2002，51：1079.

［5］ Newman M E J.The structure and function of complex networks［J］.SIAM Re，2003，45：167.

［6］ Boccaletti S，Latora V，Moreno Y，et al.Complex networks：structure and dynamics［J］.Phys Rep，2006，424：175.

［7］ Buldyrev S V，Parshani R，Paul G，et al.Catastrophic cascade of failures in interdependent networks［J］.Nature，2010，464：1025.

［8］Parshani R，Buldyrev S V，Havlin S.Interdependent networks：Reducing the coupling strength leads to a change from a first to second order percolation transition［J］.Phys Rev Lett，2010，105：048701.

［9］ Parshani R，Buldyrev S V，Havlin S.Critical effect of dependency groups on the function of networks［J］.Proc Natl Acad Sci USA，2011，108：1007.

［10］KurantM，Thiran P.Layered complex networks［J］.Phys Rev Lett，2006，96：138701.

［11］Granell C，Gómez S，Arenas A.Dynamical interplay between awareness and epidemic spreading in multiplex networks［J］.Phys Rev Lett，2013，111：128701.

［12］Nicosia V，Bianconi G，Latora V，et al.Growingmultiplex networks［J］.Phys Rev Lett，2013，111：058701.

［13］Battiston F，Nicosia V，Latora V.Structural measures for multiplex networks［J］.Phys Rev E，2014，89：032804.

［14］Baxter G J，Dorogovtsev S N，Goltsev A V，et al.Avalanche collapse of interdependent networks［J］.Phys Rev Lett，2012，109：248701.

［15］De Domenico M，Solé－Ribalta A，Cozzo E，et al.Mathematical formulation of multilayer networks［J］.Phys Rev X，2013，3：041022.

［16］D′Agostino G，Scala A.Networks of Networks：the Last Frontier of Complexity［M］.Springer，2014.

［17］Boccalettia S，Bianconic G，Criadod R，et al.The structure and dynamics of multilayer networks［DB／OL］.［2014－08－12］.http：／／arxiv.org／abs／1407.0742.

［18］Parshani R，Rozenblat C，Ietri D，et al.Inter－similarity between coupled networks［J］.Euro phys Lett，2010，92：68002.

［19］Lee K－M，Kim J Y，Cho W－K，et al.Correlated multiplexity and connectivity of multiplex random networks［J］.New J Phys，2012，14：033027.

［20］Min B，Yi S D，Lee K－M，et al.Network robustness of multiplex networks with interlayer degree correlations［J］.Phys Rev E，2014，89：042811.

［21］Hu Y，Zhou D，Zhang R，et al.Percolation of interdependent networks with intersimilarity［J］.Phys Rev E，2013，88：052805.

［22］Cellai D，Lopez E，Zhou J，et al.Percolation in multiplex networks with overlap［J］.Phys Rev E，2013，88：052811.

［23］Cohen R，Erez K，Avraham D，et al.Resilience of the Internet to random breakdowns［J］.PhysRev Lett，2000，85：4626.

［24］Callaway D S，Newman M E J，Strogatz S H，et al.Network robustness and fragility：Percolation on random graphs［J］.Phys Rev Lett，2000，85：5468.

［25］Cohen R，Erez K，Avraham D，et al.Breakdown of the Internet under intentional attack［J］.Phys Rev Lett，2001，86：3682.

［26］Cohen R，Havlin S.Complex networks：Structure，robustness and function［M］.Cambridge：Cambridge University Press，2010.

［27］李明.网络逾渗与级联故障［D］.合肥：中国科学技术大学，2014.Li Ming.Percolation and cascading failures on networks［D］.Hefei：University of Science and Technology of China，2014.

［28］Gao J，Buldyrev S V，Havlin S，et al.Robustness of a network of networks［J］.Phys Rev Lett，2011，107：195701.

［29］Gao J，Buldyrev S V，Stanley H E，et al.Percolation of a general network of networks［J］.Phys Rev E，2013，88：062816.

［30］Son S W，Bizhani G，Christensen C，et al.Percolation theory on interdependent networks based on epidemic spreading［J］.Euro Phys Lett，2012，97：16006.

［31］Newman M E J，Strogatz S H，Watts D J.Random graphs with arbitrary degree distributionsand their applications［J］.Phys Rev E，2001，64：026118.

［32］Newman M E J.Spread of epidemic disease on networks［J］.Phys Rev E，2002，66：016128.

［33］Brummitt C D，Lee K－M，Goh K－I.Multiplexity－facilitated cascades in networks［J］.Phys Rev E，2012，85：045102.

［34］Brummitt C D，D′Souza R M，Leicht E A，Suppressing cascades of load in interdependent networks［J］.Proc Natl Acad Sci USA，2012，109：E680.

［35］Kurant M，Thiran P，HagmannP.Error and attack tolerance of layered complex networks［J］.Phys Rev E，2007，76：026103.

［36］Gómez S，Díaz－Guilera A，Gómez－Garde~nes J，et al.Diffusion dynamics on multiplex networks［J］.Phys Rev Lett，2013，110：028701.

［37］Buldyrev S V，Shere N W，CwilichG A.Interdependent networks with identical degrees of mutually dependent nodes［J］.Phys Rev E，2011，83：016112.

［38］Valdez L D，Macri P A，Stanley H E，et al.Triple point in correlated interdependent networks［J］.Phys Rev E，2013，88：050803.

［39］Li M，Liu R－R，Jia C－X，et al.Critical effects of overlapping of connectivity and dependence links on percolation of networks［J］.New J Phys，2013，15：093013.

［40］Newman M E J.Mixing patterns in networks［J］.Phys Rev E，2003，67：026126.

［41］Vázquez A，Moreno Y.Resilience to damage of graphs with degree correlations［J］.Phys Rev E，2003，67：015101.

［42］Zhou D，Stanley H E，D′Agostino G，et al.Assortativity decreases the robustness of interdependent networks［J］.Phys Rev E，2012，86：066103.

［43］Kim J－Y，Goh K－I.Coevolution and correlated multiplexity in multiplex networks［J］.Phys Rev Lett，2013，111：058702.