时效复杂网络结构可控性研究

潘玉剑，李 翔

（复旦大学信息科学与工程学院电子工程系自适应网络与控制研究室，上海200433）

0 引言

现实世界中存在着各式各样的由相互关联和相互作用的若干组成部分按一定规律连接而成的整体系统，如工程系统、生物系统、经济系统、社会系统等。人们在研究这些系统的理论表述中，常常将它们抽去具体的物理或社会含义而抽象化为一般意义下的系统，这种处理方法有助于揭示系统的一般特性。代表性地，卡尔曼将状态空间法引入到对于系统的状态描述。在此基础之上，卡尔曼进一步提出了能控性和能观测性这两个表征系统特性的重要概念，它们是线性系统理论中两个最基本的概念［1－2］。网络和系统一样无时不在、无处不在［3］，网络的科学研究是从图论开始的。1736年，欧拉通过证明Koningsberg七桥问题的无解从而建立了现代数学意义下的图论。1960年前后Erdos和Renyi关于随机网络的生成及演化的奠基性工作形成了后来半个世纪数学图论的核心［4－5］。

从图论来研究以有向图表征的线性时不变动力系统的能控性始于20世纪70年代，作者们把这样的可控性研究称为结构可控性［6－8］。传统的控制理论侧重于单个高维系统内部的控制，对以图表征的节点之间存在的规则（不规则）结构没有给予充分的关注。融合图论的结构可控性更倾向于研究节点间拓扑关系对可控性的影响。换句话说，经典控制理论中的可控性强调单个个体内在动力学特性的研究，而结构可控性则从节点子系统之间存在的相互影响出发，着重研究节点子系统之间的关系对动力学的影响。前者对应的是微观个体动力学特性，而后者对应的是宏观群体的集群动力学行为。

信息技术的迅猛发展为人们在宏观层面上研究大规模和高维度的复杂网络提供了有力支持。1998年—1999年先后在《Nature》和《Science》杂志上刊发了两篇开创性文章：一篇是当时的博士生 Watts与其导师Strogatz教授的小世界网络研究论文［9］，另一篇是Barabasi教授及其当时的博士生Albert对于无标度网络的研究论文［10］。从此，复杂网络研究热潮在21世纪初迅速展开，大量的相关研究工作为我们揭示了复杂网络中存在的各种基本特征和群体现象。结合结构可控性的提出［6－8］和大规模复杂网络研究的兴起［9－10］，近年来网络结构可控性领域的研究此起彼伏、方兴未艾，有关网络结构可控性的研究工作和成果大量涌现［11－20，27－29］。本文围绕结构可控性对当前从静态网络到时效网络的研究现状进行综述。

1 经典控制理论、结构可控性及其延伸

1.1 线性系统的可控性

一个线性时不变（也称定常）系统可以用微分方程˙x（t）＝Sx（t）＋Bu（t）来表示，其中x（t）＝（x1（t），x2（t），…，xN（t））T∈RN为状态变量，S∈RN×N为系统矩阵，B∈RN×M为输入矩阵，u（t）＝（u1（t），u2（t），…，uN（t））T∈RM为输入控制变量。对于上述线性定常系统，如果存在一个分段连续的输入u（t）能在有限的时间区间［t0，t1］内使得系统由某一初始状态x（t）转移到任一指定的终端状态x（tf）（t0≤t＜tf≤t1），则称此状态是能控的。若系统的所有状态都是能控的，则称此系统是状态完全能控的，或简称系统是完全能控的。该系统完全能控的充分必要条件为：rank［B SB … SN－1B］＝N，其中N 为系统矩阵S的维数；矩阵Wc＝［B SB … SN－1B］称为系统的卡尔曼能控性判别矩阵［5，34］。通常，将上述线性定常系统简略表示为（S，B）。

相应地，一个线性时变系统可以用微分方程˙x（t）＝S（t）x（t）＋B（t）u（t）来表示。时变系统能控性的定义与定常系统的类似，只不过在这里S（t）、B（t）是时变矩阵而非常系数矩阵。对于上述线性时变系统，如果存在一个分段连续的输入u（t）能在有限的时间区间［t0，t1］内使得系统由时间t0的某一初始状态x（t0）转移到指定时间点tf的任一终端状态x（tf）（t0＜tf≤t1），则称此状态是在t0时刻能控的。若系统所有的状态在t0时刻都是能控的，则称此系统在t0时刻是状态完全能控的，或简称系统在t0时刻是完全能控的。由于系统矩阵S（t）是时变的，通常无法给出类似线性定常系统的紧凑型可控性判别矩阵的数学表达式。类似地，通常将线性时变系统简略表示为（S（t），B（t））。

1.2 静态网络的结构可控性

若将线性定常系统的系统矩阵S换成由一个表示网络拓扑关系的邻接矩阵A，方程可改写为（t）＝A′x（t）＋Bu（t），其中A′为网络邻接矩阵A的转置。从数学形式上比较改写前后两种表达形式，它们本质上并无多大区别，都是一个一阶线性常微分方程（组），但从物理意义上比较，两者意义相去甚远：1）前者的矩阵S为系统矩阵，整个表达式描述的是系统自身参数之间的相互影响和变化关系，这样的x（t）被称为参数空间；2）后者的矩阵A为邻接矩阵，整个表达式描述的是网络群体中各个个体之间的相互影响关系，这样的x（t）被称为网络空间。

在这里，后者描述的正是网络结构可控性的问题，可进一步分为两大类：第一类为判定问题，即给定输入位置信息（输入矩阵B）和输入控制器数目（输入向量u（t）），判定网络是否结构可控；第二类为优化问题，可细分为：1）在网络结构可控的前提下，给定适当的输入位置信息（输入矩阵B）来最小化输入控制器数目（输入向量u（t））。2）在网络结构可控的前提下，给定适当的输入控制器数目（输入向量u（t））来简化输入位置信息（输入矩阵B）。

为更好地阐述结构可控性相关概念及其条件，首先给出如下几个定义［2，6］：

定义1 对于一个矩阵A＊，若它的元素要么是零，要么是一个自由参量，则称矩阵A＊为结构矩阵。

定义4 对于一个由结构矩阵组成的系统（A＊，B＊），如果存在一个完全可控的定值系统），并且（，）∈（A＊，B＊），则称系统（A＊，B＊）是结构可控的。

结合上述LTI系统可控性和结构矩阵的定义，Lin［6］给出了由系统（A′，B）表示的有向网络结构可控的充要条件［6］：1）网络结构不变，即矩阵A是一个固定的结构矩阵。2）网络中不存在不可达节点，即以任一输入为起点都至少存在一条有向路径到达网络中任意其他节点。3）具有这样一种外部输入的网络中不存在扩张。若用V和U分别表示该网络本身的节点集合以及外部输入控制器集合，E和E′分别表示网络本身的边集以及存在于控制器与网络节点之间的边集，则扩张在数学上可表示为：存在一个子集Sb⊂V以及与之对应的邻集T（Sb）＝｛vj｜（vj→vi）∈（E∪E′），vj∈（V∪U），vi∈Sb｝，并且｜T（sb）｜＜｜Sb｜。

对应于上述充要条件，Lin给出了判定结构可控的图论判据，即掌状结构，它由干、枝、芽、圈以及U根因子连接等一些基本结构组成。通过直观的图论映射方式，作者把原本需要用复杂数学计算来确定的矩阵秩大小问题转化为一个纯图论问题：只要给出输入控制的数目（输入向量u（t））和位置（输入矩阵B），就能通过尝试找出网络中的掌状结构来判断该系统是否是结构可控的。

随着大规模的系统网络研究成为社会、经济、工程、生物等诸多领域的热点，人们关注的问题和焦点不仅仅是根据给定输入位置信息（输入矩阵B）和输入控制器数目（输入向量u（t））来机械式地判定网络是否结构可控（即结构可控的第一类问题），一个更为迫切的问题是如何深入理解结构可控和网络结构之间的关系，即在保证可控的前提下如何优化控制器数目（即结构可控的第二类问题）。Lombadi等［21］首次将结构可控的概念应用到物理和系统生物网络。他们发现结构可控所展示和表达的不仅仅是节点间的上下游或隶属关系，它与内在的网络结构之间存在着彼此交错且复杂微妙的关系。结合结构可控性和有向网络的匹配，Liu等［11］对上述问题给出了一个相对完整的回答。

根据文献［11，21］，首先阐述几个与有向图匹配相关的定义：

定义5 对有向图G（V，E），设M∈E。如果M中任意两条边都没有共同的起点（有向边的头）或者终点（有向边的尾），那么称M为有向图G（V，E）的一个匹配。

定义6 所有作为匹配M中边终点（有向边的尾）的节点称为网络的匹配节点，网络中其他节点均为不匹配节点。对于有向图的任一匹配M，它的匹配节点数目一定为｜M｜。

定义7 图G（V，E）尺度所有匹配中匹配节点数目最多的那些匹配称为最大匹配，本文中均用M＊表示，且｜M＊｜为常数。

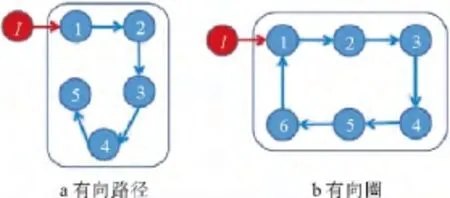
图1 由有向网络匹配中的边和节点组成的基本网路结构Fig.1 The basic structures consisted of nodes and edges in a matching of a directed network

根据上述匹配的定义，网络某个匹配中所有的边和节点可组成两种基本结构：有向路径和有向圈，如图1所示。利用Lin给出的充要条件，分别对有向路径和有向圈进行判定。首先对于有向路径，它明显存在扩张。如图1a所示，设S＝｛1，2，3，4，5｝，若不对节点1施加控制（即去掉节点I），则T（S）＝｛1，2，3，4｝，明显｜T（S）｜＜｜S｜，因此有向路径中存在扩张，结构不可控；若对节点1施加控制，此时T（S）＝｛1，2，3，4，I｝，｜T（S）｜＝｜S｜，路径中没有扩张和不可达节点，因此该有向路径结构可控。其次，有向圈不存在扩张。如图1b所示，每个节点有且仅有一个节点指向它，显然这样的结构中不存在扩张，若能保证节点可达，就能确保其结构可控。综上所述，若能保证每个不匹配节点（即有向路径的起点）都有一个独有的控制器来控制它，就可以保证网络中不存在扩张；对于有向圈，只需要从任意控制器引出一条边使得节点可达，就能保证网络中没有不可达节点。因此网络结构可控所需最小控制器数目即为网络某个最大匹配所对应的最小不匹配节点数目。

基于上述分析，Liu等［11］给出了最小输入定理：

定理1 当有向网络是一个完美匹配时（网络中所有节点均为匹配节点），需要施加的最小控制器数目为1；当网络不是一个完美匹配时，需要施加的最小控制器数目为N－｜M＊｜。数学式表达为NI＝max｛N－｜M＊｜，1｝，其中NI为最小输入控制器数目，N为网络的节点数目，M＊为有向网络的某个最大匹配。

在Liu等人工作的启发下，一系列与网络结构可控性相关的工作陆续展开：Wang等［14］通过适当改变网络结构来达到最优控制的目的；Liu等［15］进一步地提出控制中心性来衡量单个节点在网络中的控制能力大小；Nepusz等［16］在结构可控的基础上提出了网络的边控制动力学；Yan等［17］从所耗费的能量角度提出了一种衡量网络完全可控难易程度的指标，并给出了相应的范围——能量耗费大小的上下界；Sun等［18］指出在实际应用中增加控制器数目是一种确保网络结构完全可控的有效方法；Yuan等［19］在无向网络的可控性研究的基础上，从PHB判据出发，以乘数为基准提出了研究网络结构可控性的一般化模型；Ruths等［20］针对网络结构可控的模式问题，提出了将网络控制器根据其作用分为3类并进一步将实际网络划分为与之相对应的3种类型等等。

1.3 强结构可控性

值得一提的是，早在结构可控性研究初期，一些学者对结构矩阵中的自由参数假设提出了异议。他们从工程及实际应用出发，认为一个系统的很多参数是相互关联的，因此很多理论上结构可控的系统在实际中是不可控的。基于这样的出发点，学者们提出了强结构可控的概念［23－26］：

定义8 对于一个由结构矩阵组成的系统（A＊，B＊），无论其中的非零参数如何取值，系统（A＊，B＊）都是结构可控的，则系统（A＊，B＊）是强结构可控的。

在单输入情形下，强结构可控的图论判定条件最早由 Mayeda等［23］给出，后来经过Reinschke、Jarczyk及Chapman等的更正、补充和发展，逐渐形成了两大类方法来判定网络是否强结构可控［24－26］：

2）将一个网络映射成一个二分图，如果某个匹配是节点集I＋和I－之间唯一存在的匹配，那么把这样的匹配叫做约束匹配；如果匹配中不包含自环｛vi＋，vi－｝，那么这样的匹配叫做无自环匹配。对于网络A来说，通过将其非零元素用自由参数（一般用叉号）表示就可以得到结构矩阵A＊。若将结构矩阵A＊的对角元素都用自由参数（一般用叉号）替代，就可以得到修正后的结构矩阵假设B是一个n×m的输入矩阵，当且仅当网络（A B）存在一个基数为（n－m）的约束匹配同时网络（B＊）存在一个基数为（n－m）的无自环匹配时，网络（A B）强结构可控。

由此可见，强结构可控是结构可控的一种特殊情形，它所要求的条件比结构可控更为苛刻和严格。在文章［26］中，作者还用约束匹配的方法深入探讨了强结构可控的最小输入问题，同时作者给出了两种特例：一是无向的带自阻尼的路径状网络仅需要一个控制器即可保证强结构可控；二是无向的带自阻尼的完全图需要个控制器才能保证网络强结构可控。

2 时效网络结构可控性

2.1 时效网络及其时序特征

定义9 节点（个体）的交互影响不是持续存在，时间是网络的一个基本组成元素并且使得节点（个体）的交互作用具有时间上的先后次序性和不可逆性，具有这样一些特性的网络统称为时效网络。

时效网络中节点（个体）数目和交互影响均随时间而发生变化，节点（个体）间的交互明显带有时间先后顺序特征。由此可见，时效网络更强调网络连边关系的时效性，即网络连边的时间先后顺序、时延、持续时间等属性［30－34］，此外，时间维度的不可逆转的方向性也使得时效网络与传统静态网络是完全不同的。通过图2可以看到，由于网络连边时效的影响，信息传播路径具有了时效特征，即信息的传播必须遵循网络时效性这个客观因素。图2中，a、b、c、d分别表示在不同时间点上的时效网络。红色（灰色）的时间点表示过去的时间点，黑色（暗色）的时间点表示即将到来的时间点。由于网络时效性的影响，信息最终只能从节点A传播到节点B，C和F。

图2 时效网络上的信息传播Fig.2 The illustration of information propagation on a temporal network

复旦大学自适应网络与控制研究室利用高校的WIFI上网数据建立时效网络，并研究了网络的可达性、路径长度（时间长度和物理长度）和持续时间之间的关系、时效出入度之间的关系等，作者试图通过时效特征挖掘出网络中的超级传播者［33］。更进一步地，Zhang等［34］构建转移网络，该网络上的每个节点代表一个事件，而不是通常意义上的个体，研究了同时刻发生的事件的持续时间分布状况及其时效特征模体所刻画的交互行为模式。在这样的一种转移网络上，可以清楚地看到事件是如何按时序发生和展开的。更多相关内容可以参考Holme等［30，37］对时效网络研究现状所做出的综述。因此当研究对象为时效网络时，必须格外谨慎地考虑到网络时间流的不可逆性（即时间的有序性），需要从时效网络与静态网络的本质区别出发，重新思考网络的结构可控性以及其他一系列相关的网络动力学行为特征。

2.2 结构可控性——从时效网络到特征子图

研究时效网络结构可控性不能从原有的思路出发，必须有新的方向和方法。基于此，本文先提出了最大优先匹配方法（PMM）［27］。对任一时效网络，给出了两个定义：

定义10 网络中所有接触序列活跃时间点的集合称为时效网络的特征时间，它衡量时效网络的时间尺度特征，记为TC＝｛t1，t2，…，tk｝，其中ti＜ti＋1，i＝1，2，…，k－1。

定义11 相邻两个特征时间之间的间隔称为为特征片刻，它衡量某个特定网络拓扑结构在时效网络中持续时间的长短，记为IC＝｛I1，I2，…，Ik－1｝，其中Ii＝ti＋1－ti，i＝1，2，…，k－1。

基于上述定义，将一个时效网络分割成一系列的特征子图，然后从中提取出最大特征子图，最后利用这些最大特征子图来研究时效网络的结构可控性问题，具体描述为3个步骤：1）根据时效网络的特征时间TC将其划分为一个个特征片刻IC（特征片刻中网络的拓扑是静态的），在每个特征片刻中提取出网络的特征子图，然后从这些特征子图集合中提取出所需要的最大特征子图。2）将所有的节点按照一定的优先级进行排序得到优先序列VP＝｛v1，v2，…，vN｝，这里的N为网络中节点的数目。在文中作者给出3种具有代表性及可比性的优先级排序法：节点出现频率排序，这是根据局部信息来进行的排序；节点影响力排序，这是根据全局信息来进行的排序；完全随机排序。3）根据最大匹配的方法从优先序列VP由左向右逐个选取节点，以保证最大特征子图的结构可控性。

在上述操作的基础上，本文给出了一个重要的定义以及相应的定理。

定义12 通过删除一些边，把一个无向网络转换成一系列有向圈和孤立节点的操作称为图的退化，包含最少孤立节点的退化称之为完美退化。

定理2 为了使一个无向的特征子图完全结构可控，外部所需施加的最少控制器数目ND＝max（｜Visolated｜，1），其中｜Visolated｜为任意一个完美退化中所包含的孤立节点的数目。

通过这样一种转换，将原来需要在时效网络上直接研究的问题转换到一系列静态子图上来研究，使得时效网络结构可控性的研究简单直观，且不需要在方法上做出较大的变动，仿真结果也说明PMM方法很好地保留下原时效网络的时效特征。

2.3 结构可控性——从时效网络到线性时变系统

本文根据线性时变系统给出了研究时效网络结构可控性的标准化模型［28－29］。类似于将静态网络映射到一个线性时不变（LTI）系统的思路，将时效网络对映射到一个线性时变（LTV）系统x（t）＝A′（t）x（t）＋B（t）u（t）上去。从单控制器出发，输入矩阵B（t）此刻退化成一个输入向量b（o），给出了单个节点控制能力大小的衡量指标——节点的控制中心性的定义。

定义13 定义SM（o）＝rank（Wc）＝rank（［GT…G2H1…GTHT－1HT］）为时效网络节点的控制中心性，其中Gk＋1＝I＋Tk＋1A′k＋1，Hk＋1＝Tk＋1b（o），Gk＋1中的I为单位矩阵，Tk＋1为对线性系统的采样间隔，A′k＋1为k＋1时刻时效网络的邻接矩阵，Hk＋1中的b（o）为单输入控制下的输入向量，o为直接施加控制器的网络节点。

由定义13可知，当SM（o）＜N时，施加在节点o处的单个控制器可以完全控制整个时效网络；当SM（o）＜N时，SM（o）给出了施加在节点o处的单个控制器在整个时效网络中的最大可控子空间。为了从图论的角度来理解矩阵Wc所表达的含义，将时效网络中所有节点（包括控制器节点）复制T＋1次得到TOG模型，即一个规模更大但无回路的静态网络。如图3所示，所有的时间流向都用有向路径表示，这样的做法是以空间的代价换取时序特征给问题分析所带来的不便。图3中的红色虚线，黑色（暗色）实线以及蓝色（灰色）实线分别代表时间流方向，与单个控制器之间的连边以及网络中节点之间的接触连边。

在此TOG模型的基础上，进一步给出了时效网络中输入可达以及时效树的定义。

定义14 对于时效网络中的输入控制器，如果它与网络中任一节点之间都至少存在一条遵循时间先后次序路径（简称时效路径），那么就称该时效网络是输入可达的。

定义15 时效网络的一个时效树，记为TTt，即为TOG模型中的广度优先搜索生成树，记为STt，两者之间为一一对应关系。

根据广度优先搜索算法，可以在TOG模型中找出广度优先搜索生成树，同时在时效网络中找出与之对应的时效树。上述TOG模型的可控矩阵可表示为为t时刻的通信矩阵，｛Qt｝o，∀为矩阵Qt的第o行，通信矩阵Qt中At＊＝而由时效树可达向量所组成的矩阵WR＝［RTTRTT… RTT］，其中12TRTTt为t时刻时效树的可达向量。

引理1 对于单一控制其输入情形下的任一时效网络，可得rank（Wc）＝rank（W＊）＝rank（WR），其中Wc为原时效网络的可控矩阵，W＊为TOG模型的可控矩阵，WR为时效树形式的可控矩阵。

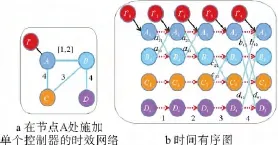
图3 将时效网络转换为静态网络方法示例Fig.3 The illustration of transformation of a temporal network to a static one

上述引理意味着只需要对简化后的时效树进行判定研究而不必在原有的时效网络上直接进行结构可控性的判定，这在数学上很大程度简化了判断矩阵Wc秩的计算量和计算复杂度。根据时效树邻接矩阵是否为同结构，将其分为两大类：第一类是邻接矩阵同结构的，称为同质结构时效树，用WS表示，第二类是邻接矩阵不是同结构的，称为异质结构时效树，用WD表示。进一步，对于同质结构时效树将其分为互相独立的时效树（对应的结构矩阵相互独立，用表示）和互相依存的时效树（对应的结构矩阵相互关联，用表示），对于异质结构时效树将其分为含有相同节点的时效树（节点相同但连接拓扑不同，用表示）和含有不同节点的时效树（节点不同连接拓扑必定不同，用表示）。

对上述4种时效树，分别给出4个引理、1个推论以及3个定理。

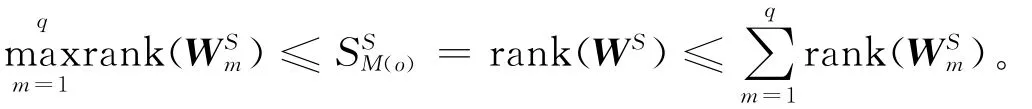
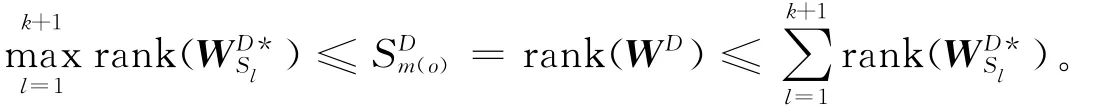
定理5 结合推论1和定理4，时效网络在单节点控制器输入情形下最大可控子空间SM（o）的上下界为：max

通过对上述两大类4种时效树中的每一种分别进行理论推导分析并给出各自所代表的最大可控子空间，结合时效树和TOG模型以及广度优先搜索生成树和时效树之间的等价性，最终给出了单节点控制器下的时效网络结构可控性——控制中心性，即单个节点的最大可控子空间，如定理5所示。利用ER模型构建了4个人工随机时效网络，每个网络均以0.002的概率在每对节点之间于每一特征时间生成一个时间接触，网络的特征时间为t＝1，2，…，100。从图4可以看到，对于这些不同网络规模的随机时效网络，控制中心性的上下界理论值之间的差值（绝对值）都相当小，这很好地说明我们的理论结论是可靠有效的。图4中控制中心性的真实值（用“Calculated”表示）是通过直接计算可控矩阵得到的，理论上下界（分别用“Upper Bound”和“Lower Bound”表示）是根据理论分析结果得到的。

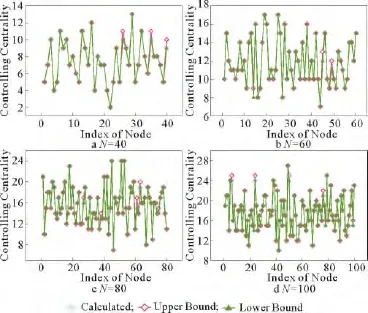
图4 ER随机网络的控制中心性Fig.4 Controlling centrality of ER random networks

此外，本文还采用3组实际数据（HT09来自2009年超文本会议采集到的与会人员之间面对面的交流信息，SG－Infectious来自于在爱尔兰都柏林的科学走廊举行的名叫“感染：保持距离”艺术科学展览会，这组数据记录下了参与展览的人之间日常的无序和动态的接触，FudanWIFI是在2009—2010年秋季学期（3个多月）复旦校园中采集到的师生无线上网的信息）生成了8个时效网络，网络规模分别为：HT09：113节点、9 856接触，73节点、3 679接触，SG－Infectious：1 321节点、20 343接触，868节点、13 401接触，2 189节点、33 744接触，Fudan WIFI：1 120节点、12 822接触，2 250节点、25 772接触，1 838节点、27 810接触。控制中心性解析解的上下界由文中解析解给出，上下界之间的差值由上下界之间的差（绝对值）给出。节点的集聚度代表的是在相应的时效网络中与该节点有过直接接触的节点的数目。与时效网络的规模（从73到2 250个节点）相比较，上下界之间的差值相对很小。图5a表示HT09数据生成的两个网络（分别用all range和removed表示）的仿真结果，图5b表示SGInfectious数据生成的3个网络（分别用Week 1、Week 2和Week 1＆2表示）的仿真结果，图5c表示Fudan WIFI数据生成的3个网络（分别用Day 1、Day 2和713point表示）的仿真结果。尽管研究的时效网络的规模是大小不等的（小到73节点、3 679接触，大到2 250节点、27 810接触），上下界之间的差值（绝对值）仍然保持在相当小的范围，如图5中所示。这进一步从实际数据方面证实了我们理论分析结论的可行性和可靠性。当我们从时效网络中移除某些重要节点（图5a中移除了时效网络中心性最大的40个节点），或者考虑同一数据中不同时间段的以及不同数据的时效网络（图5b和c中，考虑了同一数据中不同时间段所对应的时效网络以及不同数据所形成的不同类型的时效网络）时，发现节点集聚度和它的控制中心性之间的正相关关系并没有随着数据集的不同、时间段选取的不同或者网络结构的变化而发生统计上的变化。

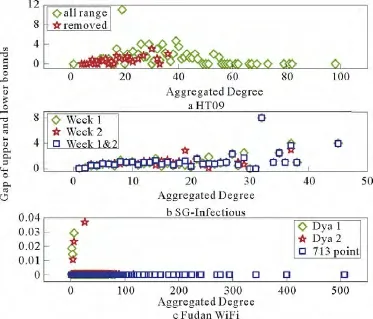
图5 节点控制中心性上下界之间的差值（绝对值）Fig.5 The gap（absolute value）between upper and lower bounds of controlling centrality

3 结语

计算机通信和电子科学技术的发展使得我们能够记录下许许多多社交信息，例如在线实时互动数据、通过电子邮箱和手机短信的通讯数据，这些数据信息扩大了我们的对象研究范围，也突破了原有的对象研究方法。随着社会科学技术的进一步发展，人们将越来越关注由上述数据生成的时效网络——一类特征明显且更为贴近实际情形的网络模型——的研究，其中有关网络的结构可控性的研究更是人们迫切希望能够深入理解并期望最终能够加以利用的一个重要方面。尽管有关网络结构可控性的工作已经在静态体系下迅猛发展并且日趋成熟，但对于动态网络，尤其是时效网络上的结构可控性研究还处于起步阶段，现有的部分工作也只是初步提出了研究规范框架和模型，大量的相关性工作还有待学者们进一步的探讨和研究。就目前来看，至少仍存在两大方面的工作有待展开：多输入控制下时效网络结构可控性问题。现实中人们往往更关注于如何设计出一个最优的控制方案或者策略，以使得整个时效网络完全结构可控，这也是我们理解和研究时效网络结构可控理论上的目标；网络可控性的对偶面——可观性。当网络的规模大到人们无法完全了解和掌握时，是否可以通过网络的可观性来反推出网络的拓扑结构。信息论中也面临着一个相似问题：当网络中存在一个或多个源头（信息源、污染源或干扰源等）时，能否通过有限的信息量来反推出信源的位置。这部分的工作具有十分重大的现实指导意义［35－36］。

［1］ Kalman R E.Mathematical description of linear dynamical systems［J］.Journal of the Society for Industrial ＆ Applied Mathematics，Series A：Control，1963，1（2）：152－192.

［2］Siljak D.Decentralized Control of Complex Systems［M］.New York：Academic Press，1991.

［3］ 陈关荣.漫谈系统与网络［J］.复杂系统与复杂性科学，2010，7（2）：1－4.Chen Guanrong.A talk about systems and networks［J］.Complex systems and complexity science，2010，7（2）：1－4.

［4］ Erdös P，Rényi A.On random graphs I［J］.Publ Math Debrecen，1959，6：290－297.

［5］ Erdös P，Rényi A.On the evolution of random graphs［J］.Selected Papers of Alfréd Rényi，1976，2：482－525.

［6］ Lin C T.Structural controllability［J］.Automatic Control，IEEE Transactions on，1974，19（3）：201－208.

［7］ Shields R W，Pearson J B.Structural controllability of multiinput linear systems［J］.IEEE Trans on AC，1976，21（2）：203－212.

［8］ Mayeda H.On structural controllability theorem［J］.Automatic Control，IEEE Transactions on，1981，26（3）：795－798.

［9］ Watts D J，Strogatz S H.Collective dynamics of‘small－world′networks［J］.Nature，1998，393（6684）：440－442.

［10］Barabási A L，Albert R.Emergence of scaling in random networks［J］.Science，1999，286（5439）：509－512.

［11］Liu Y Y，Slotine J J，Barabási A L.Controllability of complex networks［J］.Nature，2011，473（7346）：167－173.

［12］陈关荣.复杂动态网络环境下控制理论遇到的问题与挑战［J］.自动化学报，2013，39（4）：312－321.Chen Guanrong.Problems and challenges in control theory under complex network environments［J］.Acta Automatica Sinica，2013，39（4）：312－321.

［13］席裕庚.大系统控制理论与复杂网络——探索与思考［J］.自动化学报，2013，39（11）：1758－1768.Xi Yugeng.Large－scale systems control and complex networks－exploration and thinking［J］.Acta Automatica Sinica，2013，39（11）：1758－1768.

［14］Wang W X，Ni X，Lai Y C，et al.Optimizing controllability of complex networks by minimum structural perturbations［J］.Physical Review E，2012，85（2）：026115.

［15］Liu Y Y，Slotine J J，Barabási A L.Control centrality and hierarchical structure in complex networks［J］.Plos one，2012，7（9）：e44459.

［16］Nepusz T，Vicsek T.Controlling edge dynamics in complex networks［J］.Nature Physics，2012，8（7）：568－573.

［17］Yan G，Ren J，Lai Y C，et al.Controlling complex networks：How much energy is needed？［J］.Physical Review Letters，2012，108（21）：218703.

［18］Sun J，Motter A E.Controllability transition and nonlocality in network control［J］.Physical Review Letters，2013，110（20）：208701.

［19］Yuan Z，Zhao C，Di Z，et al.Exact controllability of complex networks［J］.Nature Communications，2013，4：2447.

［20］Ruths J，Ruths D.Control profiles of complex networks［J］.Science，2014，343（6177）：1373－1376.

［21］Lombardi A，Hörnquist M.Controllability analysis of networks［J］.Physical Review E，2007，75（5）：056110.

［22］Hopcroft J E，Karp R M.An n5／2algorithm for maximum matchings in bipartite graphs［J］.SIAM Journal on Computing，1973，2（4）：225－231.

［23］Mayeda H，Yamada T.Strong structural controllability［J］.SIAM Journal on Control and Optimization，1979，17（1）：123－138.

［24］Reinschke K J，Svaricek F，Wend H D.On strong structural controllability of linear systems［C］／／Proceedings of the 31st IEEE Conference on Decision and Control.IEEE，1992：203－208.

［25］Jarczyk J C，Svaricek F，Alt B.Strong structural controllability of linear systems revisited［C］／／CDC－ECE，2011：1213－1218.

［26］Chapman A，Mesbahi M.On strong structural controllability of networked systems：a constrained matching approach［C］／／American Control Conference（ACC），IEEE，2013：6126－6131.

［27］Pan Y，Li X，Zhan J.On the priority maximum matching of structural controllability of temporal networks［C］／／Control Conference（CCC），2013 32nd Chinese，IEEE，2013：1164－1169.

［28］Pan Y，Li X.Towards a graphic tool of the structural controllability of temporal networks［C］／／International Symposium on Circuits and Systems（ISCAS），Australia IEEE，2014.

［29］Pan Y，Li X.Structural controllability and controlling centrality of temporal networks［J］.PloS one，2014，9（4）：e94998.

［30］Holme P，Saramäki J.Temporal networks［J］.Physics Reports，2012，519（3）：97－125.

［31］Kim H，Anderson R.Temporal node centrality in complex networks［J］.Physical Review E，2012，85（2）：026107.

［32］Isella L，StehléJ，Barrat A，et al.What′s in a crowd？Analysis of face－to－face behavioral networks［J］.Journal of Theoretical Biology，2011，271（1）：166－180.

［33］Zhang Y，Wang L，Zhang Y Q，et al.Towards a temporal network analysis of interactive WiFi users［J］.EPL（Europhysics Letters），2012，98（6）：68002.

［34］Zhang Y Q，Li X.Temporal dynamics and impact of event interactions in cyber－social populations［J］.Chaos：An Interdisciplinary Journal of Nonlinear Science，2013，23（1）：013131.

［35］Shah D，Zaman T.Rumors in a network：who′s the culprit？［J］.IEEE Transactions on Information Theory，2011，57（8）：5163－5181.

［36］Pinto P C，Thiran P，Vetterli M.Locating the source of diffusion in large－scale networks［J］.Physical Review Letters，2012，109（6）：068702.

［37］Li X，Zhang Y Q，Vasilakos A V.Discovering and Predicting Temporal Patterns of WiFi－Interactive Social Populations［M］／／Wu J，Wang Y S.Opportunistic Social Mobile Networks，CRC Press，2014.