基于复杂网络的体系作战协同能力分析方法研究

胡晓峰，贺筱媛，饶德虎，2

（1.国防大学信息作战与指挥训练教研部，北京100091；2.海军工程大学电子工程学院，武汉430033）

0 引言

战争系统包含作战体系、国家关键基础设施体系，社会群体体系等诸多不同的体系，以及连接它们的信息网络体系，涉及物理域、信息域和认知域等多个领域空间，跨域作战体系成为信息化战争的主要研究对象，考察和研究作战体系在多域空间的对抗十分重要。以信息为主导、以网络为中心的信息化战争，使作战体系内部之间的关联更紧密，相互作用更强，体系对抗整体性效果更为突出，这种以信息网络为中心的联合，比以往更加强调整体效能的发挥，“指挥”和“协同”成为影响作战体系整体效能发挥的关键。

信息时代的体系作战无限放大了战争复杂性，对揭示战争复杂性和体系作战规律的需求日益强烈。然而，传统的以战争实践和历史总结为主的研究方法，在对作战体系复杂性分析中正面临以下3个挑战：一是体系作战的规模庞大，体系性质不具可加性，仅仅分析局部不可能得到整体性结果，如何对其进行整体性分析；二是作战体系的组分之间交互复杂，其结构动态变化，具有自适应、自组织、因果关系不明确、结果不唯一等性质，如何反映其复杂性特点；三是体系对抗是由指挥员所主导的，其本质是人与人之间的对抗，而人是有“自由意志”的，如何纳入对人的因素分析。面对上述3个方面的挑战，仅靠“分解还原”认识世界的方法显然已难以揭示信息时代体系对抗的复杂性特点。

分析体系作战过程中的指挥和协同效果，关键是对以下两个问题找到相应的分析方法。一是如何对“系统的系统”——作战体系进行建模，建立起包括通信网、指控网、传感网等不同网络及其相互关系的网络模型；二是以何种角度对体系作战中指挥和协同进行评估，从作战效能上讲，就是作战体系的协同效果如何度量，重点是如何对不同作战行动之间的协调性进行度量。

本文从复杂性科学视角，运用网络科学开创的研究范式——基于数据的复杂系统数学模型，以崭新的视角和研究手段，对体系作战中的指挥与协同效果进行研究。一方面，采用复杂网络建模方法刻画信息化战争体系对抗的整体性及复杂性特点；另一方面，对有人参与的指挥对抗演习过程中生成的仿真大数据进行分析，找到影响作战体系的演化要素之间的关系，甚至探寻更深层次的在人的指挥行为干预下的作战体系演化原因。

1 基于复杂网络的体系作战超网络建模

信息时代的主要战争形态是体系作战。为刻画信息化条件下体系作战的非线性、适应性和涌现性等特征，需要建立以作战决策过程动态循环的控制主线，综合反映物理域、信息域与认知域三域特点的作战体系网络描述框架。

1.1 体系作战超网络建模

从网络科学的角度来看，作战体系网络是传感网、通信网、指控网和交战网综合后的“网络的网络”，是以交战（物理毁伤与信息对抗）、指控、通信、感知和融合实体为节点，各实体间的能量、信息和认知交互为边，构成的具有多层次、多维性、多级性、多属性和多目标等特征的网络。因此，作战体系网络中的节点是具有不同功能的异质节点，链路是具有信息、能量与认知的多重边，整体结构具有动态对抗的时变性，需要新的方法来研究这种多层、异质和动态的作战体系网络，而超网络的思想与方法正好为作战体系网络的描述与建模提供了思路与参考［1－3］。从物理域、信息域和认知域（共三层）划分作战体系网络，对体系作战超网络的定义是：体系作战超网络是指由物理域、信息域和认知域中不同作战要素，按照网络化的组织指挥关系和作战机制构建的三层复杂网路。用来表示体系作战超网络，则：

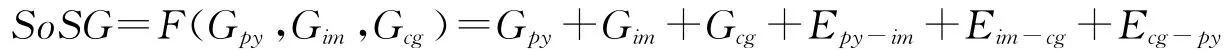
如图1所示，其中，Gpy，Gim，Gcg分别表示体系作战超网络在物理域、信息域和认知域上的三层网络。底层是物理域上依托物理实体间交战事件在物理空间形成的交战网络；中间层是信息域上依靠信息装备平台间信息流转形成的信息流网络；顶层是认知域上指挥员及其指挥机关之间根据指挥关系形成的指挥网络。Epy－im表示物理域与信息域间的交互关系；Eim－cg表示信息域与认知域间的交互关系；Ecg－py表示认知域与物理域间的交互关系。网间关系则体现了不同域上作战实体的多种影响关系，如认知空间网络与信息空间网络之间存在指挥活动的映射，某一指挥活动可能依赖多条物理链路进行。

1.2 体系作战超网络的各层网络建模

利用超网络对作战体系进行网络化分析时，仍需要对体系作战超网络中的节点与边进行抽象和建模。

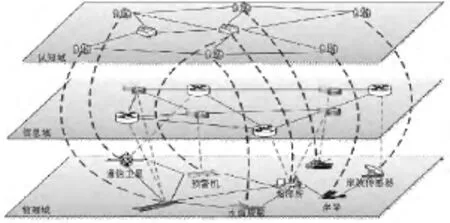
图1 体系作战超网络三层视图Fig.1 The three－layer view of SoS supernetwork

1）体系作战超网络在物理域上的交战网络。交战网络中节点是隶属不同作战集团的作战实体的并集，交战事件也应该只发生在不同作战集团之间，体系作战超网络中交战网络主要体现物理域上交战毁伤效果。因此，交战网络是满足二分图条件的二分网络，即：

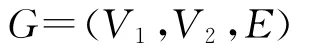
其中，V1＝｛v11，…，v1m｝表示红方作战实体的节点集合，为非空有限集；V1＝｛v21，…，v2n｝表示蓝方作战实体的节点集合，为非空有限集；V1∩V2＝Φ；E代表V1和V2之间的交战关系，E⊆V1×V2。

2）体系作战超网络在信息域上的信息网络。从功能上讲，信息网络是依靠不同通信方式在作战体系网络节点中传递信息，是一个人工功能网络。对战场信息获取、传输、加工和利用等作战环节主要是通过网络化的信息装备类实现，具体体现在传感器、通信中心、干扰设备和情报站等装备实体，与体系作战超网络中探测节点（VS）、情报节点（VI）、通信节点（VC）和信息对抗（VJ）节点等相对应。即信息网络是一个二元组有向网络，可描述为

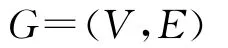
其中，V＝VS∪VI∪VC∪VJ表示信息网络中的节点集合，为非空有限集；E代表VS，VI，VC和VJ之间的信息流转关系。

3）体系作战超网络在认知域上的指控网络。人是战争中不可忽略的重要因素，尤其指挥员决策的正确与否将直接导致作战行动能否成功。各类指挥员可统称为决策节点（VD），其主要功能是接受来自探测节点或情报节点的信息与感知态势，并就当前或将来其他节点的部署做出决策。故指控网也可用一个二元组有向网络来描述，即：

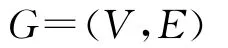
其中，V＝VD表示指控网络中决策节点节点集合，为非空有限集；E代表VD之间的指挥与控制关系。

4）体系作战超网络的网间关系。体系作战超网模型是作战实体在物理域、信息域和认知域上的抽象，对一个具体的实体（虚拟的或者物理的）而言，是同一实体在不同网上的映射。网间关系在不同的层之间表现出不同的特点，并且方向不同，效用也不尽相同，主要分为以下4类：

（1）物理网到信息网的网间关系。物理网与信息网中节点之间的关系主要表现为两类，一类是节点之间的物理依赖性构成的映射关系，描述了同一节点的物理属性与信息属性的统一性，物理层节点的物质和能量属性将不同程度地影响信息层节点的信息属性。这种映射关系，可以形式化描述为

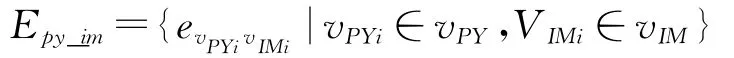
物理网到信息网的另一类关系是物理域中探测节点探测到的目标信息传递给信息网的信息传递关系，可以用目标信息流Flowtarget来表示：

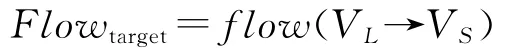
目标信息流Flowtarget的发起端是物理层的节点VL，接收端是信息层的VS，这里VS主要是信息网中的探测类节点。VL传递给信息层的目标信息流将会在信息层融合，不准确或者不及时的目标信息必然导致融合形成的态势信息的不准确，或者影响态势融合消耗的时间。

（2）信息网到指控网的网间关系。从信息网到指控网的关系是信息网中的态势信息被认知层中的指挥员认知的过程，其网间关系可以用两层节点之间的关系表示为边的集合：

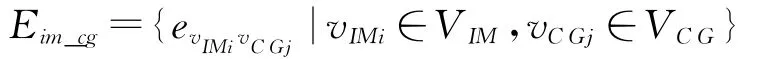
用态势信息流Flowsituation描述该过程，形式化描述如下：

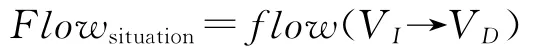
态势信息流Flowsituation的发起端是信息网中的情报融合节点VI，接收端是指控网的VD。VI传递的不准确的态势信息将会对认知层的认知产生的知识有影响，既可能产生错误的知识混淆认知层的VD决策过程，也可能延缓认知层的知识形成时间。

（3）指控网到信息网的网间关系。指挥员是通过获取战场态势信息后，再进一步进行判断来形成决策，故基于战场态势信息和指挥员知识形成决策的过程就是指控网对信息网的关系。从信息流的视角，可认为指控网到信息网的关系主要表现为决策信息流Flowdecision：

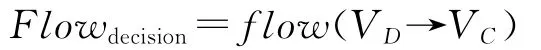
Flowdecision中包含了对信息层的信息任务和物理层的火力任务两类信息，但是都是通过信息层的节点接收，再在信息层网络内流通或者传递到物理层网络的火力打击节点，决策节点VD的处理速度等属性影响信息流的效率，指挥层级与跨度影响信息质量。

（4）信息网到交战网的网间关系。信息网接收到来自指控网中指挥员的决策信息后，将其分解成各类指挥控制信息，并在信息网内流通。从信息流的内容来说，主要表现为指挥控制信息流Flowconduct，其形式化描述为

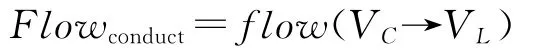
Flowconduct的发起端是信息网中的通信节点VC，接收端是交战网中的火力打击节点VL，指控信息流的主要内容是特定行动的命令信息。该信息的传递将直接影响火力打击节点完成任务的精度和速度，或者说是影响火力打击节点的能力。体系作战超网的网间关系可以用图2来描述。

2 基于体系作战超网络的作战自同步分析

体系作战自同步是指各作战单元在上级指挥控制下，在完成具体作战任务过程中涌现出的整体效果［4］。体系具有涌现性，在信息化战争中，最期望作战体系的相变就是同步。信息时代战争的主要特征是基于信息系统的体系作战，而体系作战指挥就是一个面向若干复杂体系、对强对抗性活动进行组织管理的实践活动［5］。因此，作战指挥是体系各组分在作战过程中相互作用及动态演化的内在动力，作战协同则是体系成长的“满意”目标。因此，探究体系生长与演化行为机制的动力学模型，是体系作战协同研究的主要目标。

2.1 体系作战中的作战环建模

1）基于作战环的作战协同。OODA环是对体系作战行动整个过程的一种高度抽象，能够较为清晰地描述整个作战行动的全过程。体系作战与OODA的每个环节以及作战网络的结构密切相关。从体系作战超网络的视角来看，一次体系作战行动涉及横跨指控网、信息网和交战网的多类要素并构成跨域的回路。为此，本文提出了作战环的定义，即作战环是由完成观察、判断、决策、行动等四大在作战行动的OODA环要素构成，涉及到对战场态势的感知、理解、判断、决策等多种跨域行为。如图3所示，体系作战可以看成是用多个OODA环嵌套关联耦合的系统，体系作战过程中的指挥协同将不仅仅是指挥员与指挥员之间协商，而应是指挥员在信息系统支撑下基于OODA环的指挥过程的协同。

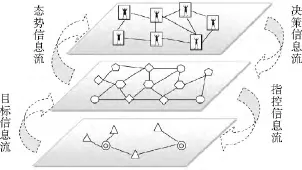
图2 体系作战超网层间关系概念视图Fig.2 The relationship view of SoS supernetwork

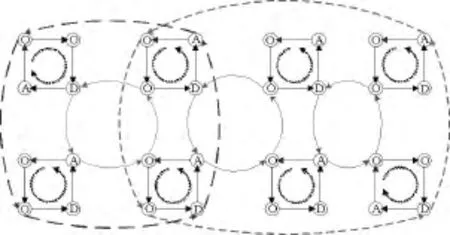
图3 基于作战环的体系作战协同过程Fig.3 SoS collaboration process based on operation loop

2）体系作战超网中的作战环建模。体系作战的作战环包含了指挥员、信息系统和作战实体等要素。从体系作战超网模型的视角看，作战环是由物理网、信息网和指控网三层网的节点构成的链路，战场态势演变将由敌我双方的作战环所共同触发。因此，体系作战中基于态势的指挥实际就是基于作战环的指挥。

体系作战中的指挥协同是为达成共同的作战目的，作战部队在指挥员的命令下完成的作战行动，强调完整的OODA环。因此，从指挥协同的作战意义上讲，体系作战超网络就可视为由作战环构成的单层同质节点网络。这样，可基于体系作战超网建立基于作战环的体系作战协同网络，其过程如图4所示。

由上可知，一次完整的作战指挥行动过程是指控网中节点所代表指挥主体在信息网络支援保障下，指挥交战网中节点所代表指挥客体完成一次物理上的作战行动。因此，作战行动所对应的作战环必然包括一个指控网节点、交战网节点和至少一个信息网络节点，从而形成一个如图4d所示的以作战环为节点，信息交互为连边的指挥协同网络，从而将跨域的体系作战三层超网络“压缩”成单层同质节点网络。

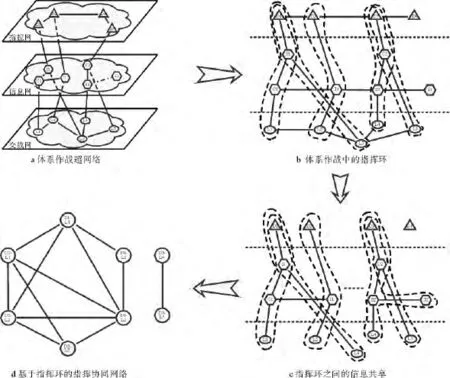
图4 基于超网络提取作战环示意图Fig.4 Illustration of operation loop extraction from supernetwork

2.2 体系作战的协同动力学模型

Kuramoto于1975年提出的耦合振子同步模型是研究同步现象的经典模型之一，鉴于模型中描述振子状态量的相位量可归属4个象限，而Boyd提出的OODA指挥控制过程也基本对应4个阶段，因此，国内外早有学者将Kuramoto模型应用于指挥协同领域的研究［6］。

体系作战协同动力学模型。体系作战作战环网络中每个节点代表着一个基于OODA的作战指挥过程，显然，每个作战环节点有一个指挥周期与之对应，且其状态沿OODA环周期变化，本文借鉴Kuramoto模型建立体系作战作战环网络的协同动力学模型：

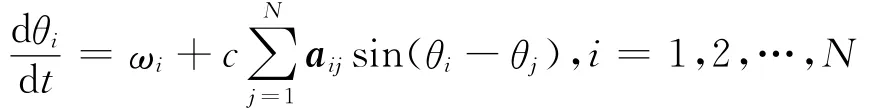
网络中作战环节点i的时变状态可用相位参数θi（t）来描述，可建立相位值与OODA环之间的映射关系；网络中作战环节点的指挥周期为Ti＝2πωi，代表了作战指挥的快慢程度。一般而言，它与作战节点获取、传输、处理以及应用战场信息的能力是密切相关的；A＝（aij）∈RN×N为体系作战作战环网络拓扑结构的邻接矩阵，若作战环节点i与作战环节点j（i≠j）之间存在耦合关系，则aij＝aji＝1；否则aij＝aji＝0（i≠j）。

信息化战争条件下，体系作战中各作战实体之间交互的信息价值是随时间演化且呈现出非线性衰减特性的，因此必须对体系作战作战环网络的协同动力学模型进行适应性改造。在网络节点的动态特性上引入二次非线性限制衰减方程f（Δθ）＝1／（2e－λΔθ－1），其中λ是反映外部环境与节点处理能力的影响因子。此时，体系作战作战环网络的协同动力学方程为

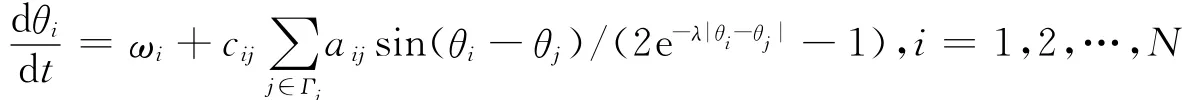
从该模型的定义可知，在体系作战协同过程，影响作战体系整体动态同步性能主要涉及以下3个因素：一是作战实体之间指挥权力的差异将影响方程中作战环耦合强度c的变化，而它正是驱使网络同步的动力；二是作战实体类型与性能上的差异将影响协同动力学方程中信息演化价值λ的变化，而它也是网络整体失调的源头之一；三是体系作战作战环网络的整体拓扑结构的变化，它将直接导致邻接矩阵A的变化，而它也是引导网络同步的方向。

2.3 体系作战的自同步能力

体系作战协同的最高境界是自同步，即各作战单元能够在共同作战任务背景下，根据感知与共享的战场态势实施自适应的作战指挥。

1）体系作战协同网络的同步判据。在体系作战作战环网络的同步现象研究中，一般选择度量网络同步全局一致性的全局序参量［7－10］为

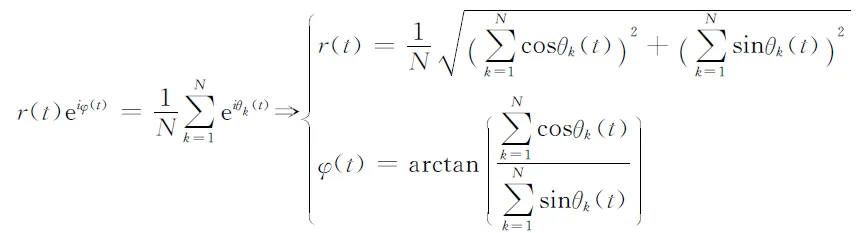
其中，0≤r（t）≤1参数在一定程度上描述了网络中形成同步节点数量占整个网络中节点数的比例，测度的是整个作战体系随时间演化后的最终协同效果。r（t）＝0说明整个作战体系中各作战节点的作战节奏各异，没有形成作战合力；r（t）＝1则表明作战体系所有节点达到作战同步。

对于体系作战作战环网络的全局序参量r（t），如果所有的t＞Tsync，存在一个相当小的正实数常量σ，对于任意Δt＞0，均能使｜r（t＋Δt）－r（t）｜＜σ成立，就称体系作战作战环网络达到同步稳定状态。稳定同步时间Tsync则是指体系作战作战环网达到同步稳定状态所需的最小时间。

一般而言，如果信息化战争中作战环网达到自同步的作战环越多、且所需时间越短，说明能够步调一致地实施作战行动的作战力量越多，产生的作战效能也越大，其指挥协同能力也越强。因此，达到同步稳定状态时的体系作战作战指挥协同能力Esync为

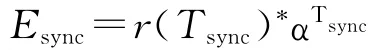
其中，r（Tsync）是全局序参量r在同步稳定状态的均值，Tsync为稳定同步时间，0＜α＜1是稳定同步时间对指挥协同能力的调节因子。

2）体系作战中作战环的互同步判据。全局序参量是从宏观与整体的意义上描述作战体系的协同效果，但如果仅仅立足于宏观层面（大尺度），只从体系作战的结果上分析其统计规律，常常只能看到战争的开始和结束，而容易掩盖实际作战指挥过程［11］。因此，为研究体系作战同步的演化路径，定义一个度量不同节点对之间的协同相关系数：

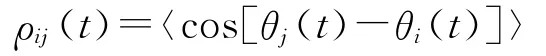
其中，ρij（t）是节点对之间相对初始状态的平均值，一般满足随时间单调递增。D＝（ρij）为作战体系协同网络的互相关矩阵，其随时间演化可揭示作战体系协同中节点形成群或社团的路径。为抽取出体系作战协同互相关矩阵的结构变化信息，可设置互相关阈值将互相关矩阵转换为“0－1”布尔矩阵。定义动态连通矩阵为：

显然，特定时间切片上，互相关阈值的变化将得到反映不同社团结构的动态连通矩阵；而对固定互相关阈值T，将得到不同时间尺度的动态连通矩阵结构的变化信息。动态连通矩阵的特征值谱S（D（T））中零特征值个数确定了作战体系网络中互不连通社团的个数［12－14］。零特征值个数越多，作战体系网络更多地呈现出未同步的孤立节点；而随着零特征值的减少，作战体系网络逐渐呈现出具有层次化结构的社团结构［15－17］。

3）体系作战中作战环的同步路径。体系作战指挥的最终目标都是自同步，但“胜战不复”的道理却告诉我们，研究作战体系从紊乱、无序状态转向整体步调一致的作战过程，对认识指挥规律更有作用［19］。从复杂网络的角度，为探究同步状态的形成过程，在中观尺度上定义一个局部序参量来描述网络如何形成同步模式：

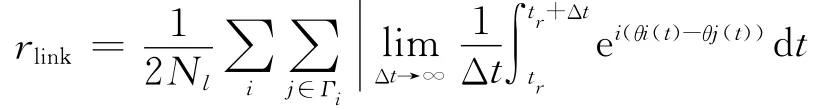
其中，Nl为网络中所有连边数量，Γi为节点i的邻居节点集。从定义上可以看出，rlink是网络中达到同步的节点对之间连边占网络所有连边的比值。

复杂网络从无序演化到全局同步过程中，必然包含只有部分节点同步的中间状态，通过定义同步块Gs、同步块数量Nc和最大同步块节点个数GC等3个序参量来描述网络同步过程的中间状态。

同步块Gs定义为网络中达到同步的连通子集；若同步块Gs中节点数为M，显然Gs满足：

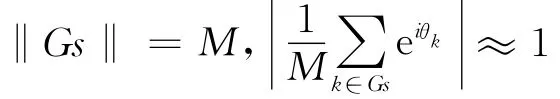
同步块数量Nc定义为网络中达到同步的连通子集数量；最大同步块节点数GC定义为网络中达到同步的最大连通子集中节点的数量，即：

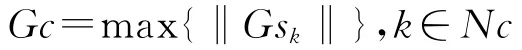
3 联合作战体系分析示例

本文采用某次演习过程中采集的仿真数据，分别从3个训练阶段中抽取仿真时间为一天的数据进行实证研究。首先，分别统计各个阶段的网络拓扑结构特征参数。红方作战体系在3个阶段中作战环网的结构特征参数如表1所示。蓝方作战体系在3个阶段中作战环网的结构特征参数如表2所示。

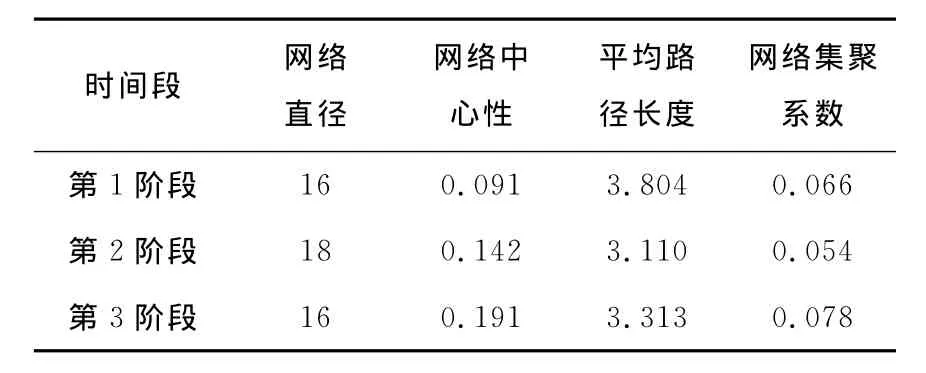
表1 红方作战环网的网络特征参数Tab.1 The Red party′s operation loop characters

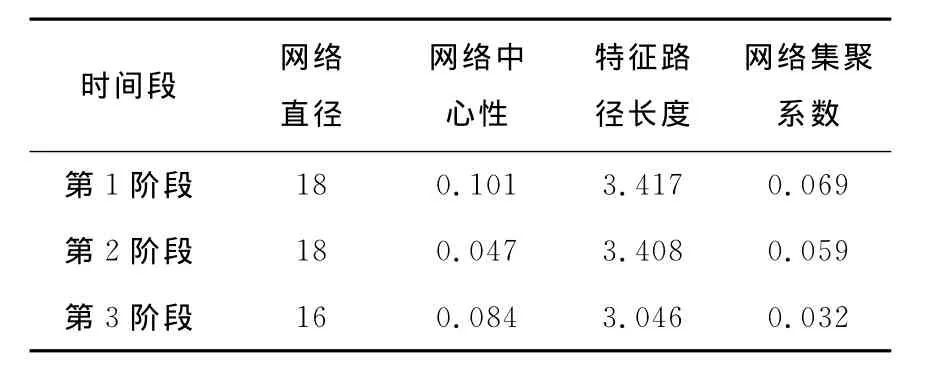
表2 蓝方作战环网的网络特征参数Tab.2 The Blue party′s operation loop characters

其次，根据体系作战协同动力学模型，对不同阶段作战环网络的自同步能力进行对比分析。其中，红、蓝双方作战环网络自同步能力如图5和图6所示。从图5可以看出，红方达到同步所需时间最短的为第1阶段；而作战体系的整体协同能力最强的为第2阶段。从图6可以看出，蓝方在第1阶段基本无法形成有效自同步；而在第3阶段达到同步所需时间最短，且整体协同能力也最强。

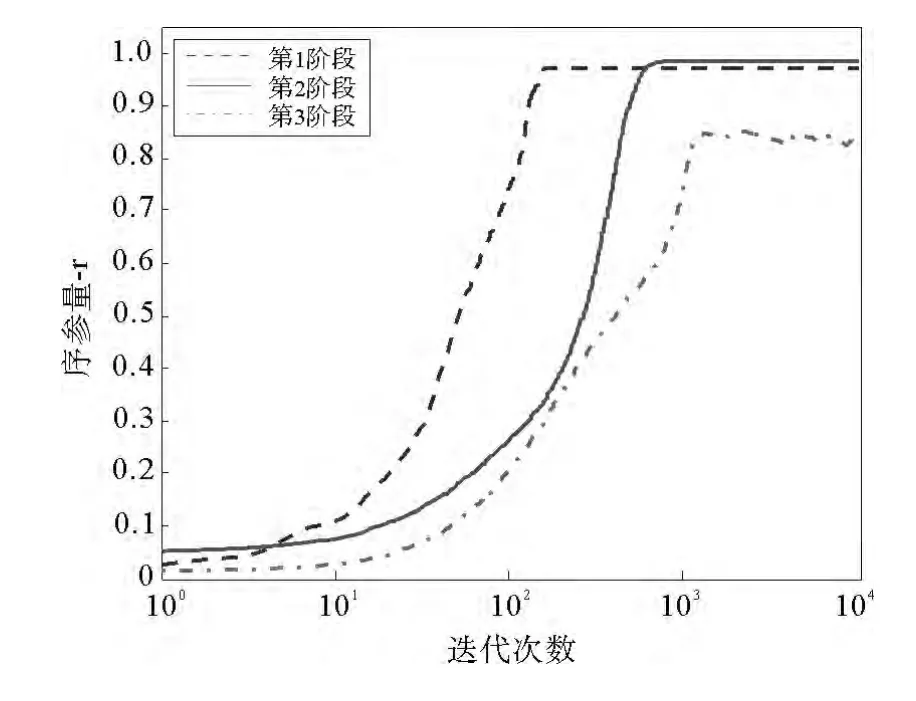
图5 红方作战环网的自同步能力图Fig.5 Synchronization ability for the Red party

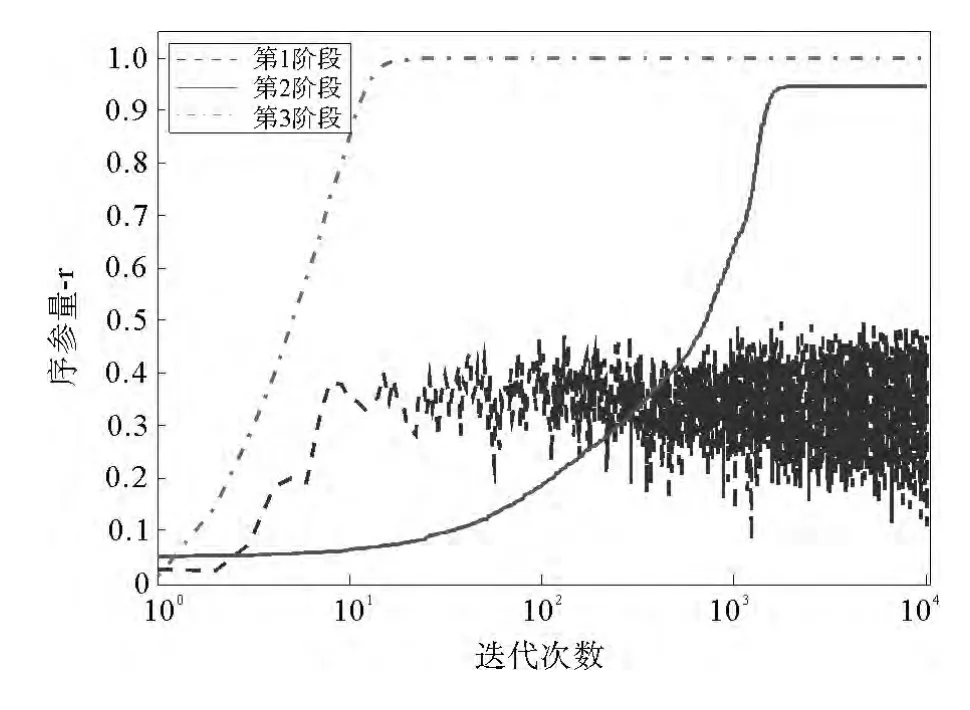
图6 蓝方作战环网的自同步能力图Fig.6 Synchronization ability for the Blue party

最后，针对红方作战环网络中作战环之间互同步能力大小，利用SAS－JMP10.0工具对所有作战环进行聚类分析，其中，蓝色代表同步时间最短，红色最长，中间为灰色。红方在3个阶段作战环之间互同步能力结果如图7所示。蓝方在3个阶段作战环之间互同步能力结果如图8所示。

作战体系的自同步能力在很大程度上决定了战争的成败，而同步能力的相对大小与指挥权限、信息演化价值和网络拓扑结构又密切相关，指挥员必须根据当前战场态势灵活决策，不断提升作战体系的整体协同能力。因此，不能脱离战场态势而论断某种指挥关系就一定比其他指挥关系要好。如，红方在第1阶段中出现抱团现象，实际上是指挥权限下放后出现的一种情况，此时作战环网络已从无标度网络向随机网络过渡，此时同步状态就呈现出抱团趋势。

图7 红方作战环网的互同步能力图Fig.7 Co－synchronization ability for the Red party

图8 蓝方作战环网的互同步能力图Fig.8 Co－synchronization ability for the Blue party

4 结语

本文分析了信息化条件下体系作战的特点，采用超网建模的方法，描述了包含交战网、信息网、指挥网三层结构的体系作战超网络模型，该模型既可支持单独研究多域单层网络的演化规律，也可根据超边、作战环来研究跨网、跨域的作战过程。研究了利用体系作战超网模型的超边构建和提取OODA作战环的方法，并建立基本作战环的作战体系同步模型，该模型通过定义并分析作战环的同步程度，来度量体系作战的同步能力和协同效果。基于上述建模研究的成果，利用真实指挥员参加的联合作战体系对抗推演产生的仿真数据，进行了体系作战同步能力的实例分析，分析结果表明，3个阶段的同步能力及演化特点，可以较好体现和解释各阶段所担负的作战任务及作战特点，从而验证了本文所研究的建模方法及分析方法的合理性与可行性。

战争充满不确定性、偶然性与不可重复性，以牛顿科学体系为奠基石形成的还原论方法、绝对时空观和因果对应观的科学研究范式，已难以找到把握现代战争运行机理、破解信息化战争制胜规律的数学公式，迫切需要从复杂性科学的角度，找出符合信息化战争特点的管控方法。研究信息化战争制胜机理是时代赋予的重要命题，我们利用复杂网络科学方法和真人参与的仿真演习数据，研究体系作战协同能力的分析方法和途径，是体系分析研究中的一次有益尝试，它对理解作战体系乃至未来控制作战体系，将产生积极的影响作用。

［1］ Nagurney A，Dong J.Supernetworks：Decision－Making for the Information Age［M］.United Kingdom：Elgar Edward Publishing，2002.

［2］ 王众托，王志平.超网络初探［J］.管理学报，2008，5（1）：1－8.

［3］ 王志平，王众托.超网络及其应用［M］.北京：科学出版社，2008.Wang Zhiping，Wang Zhongtuo.Elementary study of super networks［J］.Chinese Journal of Management，2008，5（1）：1－8.

［4］ 胡晓峰著.战争工程论——走向信息时代的战争方法学［M］.北京：国防大学出版社，2012.

［5］ 权良涛.基于复杂网络理论的作战体系网络建模研究［D］.西安：西安电子科技大学，2012.Quan Liangtao.Research on network modeling of combat system based on theory of compler network［D］.Xi′an：Xidian University，2012.

［6］ Kalloniatis A，Fairbairn D E.A new paradigm for dynamical modelling of networked C2processes［C］.Proceedings of the 13th International Command and Control Research and Technology Symposium.2008：17－19.

［7］ Motter A E，Zhou C S，Kurths J.Enhancing complex－network synchronization［J］.Europhysics Letters，2005，69（3）：334.

［8］Zeng A，Son S W，Yeung C H，et al.Enhancing synchronization by directionality in complex networks［J］.Physical Review E，2011，83（4）：045101.

［9］ 陈娟，陆君安.复杂网络中尺度研究揭开网络同步化过程［J］.电子科技大学学报，2012，41（1）：9－11.Chen Juan，Lu Jun′an.Mesoscales reveal synchronization processes in complex networks［J］.Journal of University of Electronic Science and Technology of China，2012，41（1）：9－11.

［10］Pereira T.Hub synchronization in scale－free networks［J］.Physical Review E，2010，82（3）：036201.

［11］Shandilya S G，Timme M.Inferring network topology from complex dynamics［J］.New Journal of Physics，2011，13（1）：013004.

［12］Lehnert J，Dahms T，Hövel P，et al.Loss of synchronization in complex neuronal networks with delay［J］.EPL（Europhysics Letters），2011，96（6）：60013.

［13］Sorrentino F，Ott E.Network synchronization of groups［J］.Physical Review E，2007，76（5）：056114.

［14］Motter A E，Zhou C，Kurths J.Network synchronization，diffusion，and the paradox of heterogeneity［J］.Physical Review E，2005，71（1）：016116.

［15］Donetti L，Hurtado P I，Munoz M A.Network synchronization：optimal and pessimal scale－free topologies［J］.Journal of Physics A：Mathematical and Theoretical，2008，41（22）：224008.

［16］Dahlhaus R，Neddermeyer J C.On the relationship between the theory of cointegration and the theory of phase synchronization［DB／OL］.［2014－08－03］.http：／／www.researchgate.net／researcher／46255203＿Jan＿C＿Neddermeyer.

［17］Barrat A，Barthelemy M，Vespignani A.Dynamical Processes on Complex Networks［M］.Cambridge：Cambridge University Press，2008.