高速针刺机构优化设计

广东职业技术学院机电工程系 梁铭 天津工业大学机械工程学院、天津市现代机电装备技术重点实验室 鲁喜 李浩 姜海涛 杨建成/文

1 引言

在各种各样的针刺设备中，机械原理是相同的（除圆形针刺机以外），它们的共同特点是都采用偏心（曲柄）连杆机构驱动针梁。当主轴做旋转运动时，针板和刺针作上下往复运动，刺针穿越针刺区（即穿过剥网板、纤网层、托网板），通过完成针刺原理而形成非织造布。同时，在针刺工序过程中喂入与输出速度相配合，以间歇步进或连续运动。

针刺机构是针刺机的关键机构，对纤网的针刺固结主要由其完成。它由曲柄箱、针梁、针板、刺针等组成。针刺频率的高低对生产效率和产品质量都有影响，所以提高针刺频率是设计针刺机构的关键。但目前针刺生产线的运行速度还不到10m/min,其中直接影响生产效率和成本的是针刺机的针刺速度。

本文主要分析了针刺机构中曲柄和连杆尺寸对针刺速度和针刺机的影响，对针刺机构进行优化，使针刺机运动平稳，提高生产效率。

图1 双轴双曲柄原理示意图

2 针刺机构工作原理

针刺机的上下往复运动采用偏心连杆机构，由于偏心连杆机构会产生不平衡量，影响针刺的频率和效率，所以针刺机设计对平衡机构的要求十分高。

该机构的工作原理是利用主轴带动偏心轮和平衡轮旋转，并通过连杆带动针粱和针板作上下重复运动使针板上的刺针反复穿刺棉网。

用横杆连接于一端输出。其原理图如图1所示。

机构简图如图2所示。

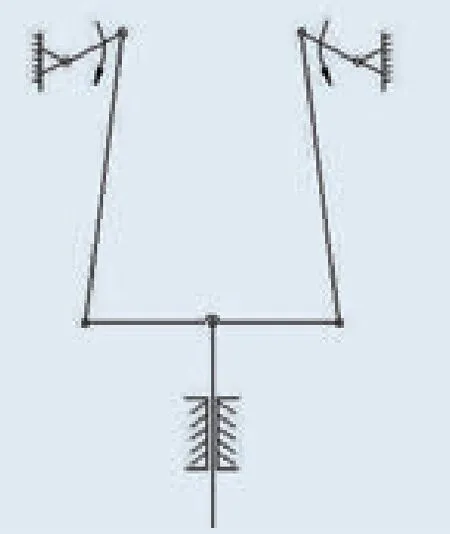
图2机构简图

3 针刺机构运动学分析

如图2所示，针刺机构由双曲柄—摆杆机构组成，两个偏心轮（曲柄）为动力源，两轮的转动方向相反，且相位差为180°。采用这种对称机构的形式除能满足机构自由度的要求外，还能在机构水平方向起到平衡惯性力矩的作用，有效减小机械振动。

在针刺机构对纤网进行针刺加工时，针刺机构做平面运动，因此针刺机构可以看为平面机构，并且在作运动和动力分析时，将机构的运动构件看成刚形体，这样就可以在针刺机构运动平面内对其进行运动学和动力学分析。此外，模型建立的前提条件是：曲柄做匀速转动且不考虑运动副中摩擦力。图3为针刺机构平面示意图。

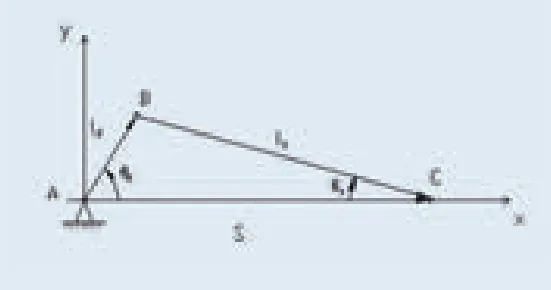
图3针刺机平面机构矢量图

对平面机构的运动分析法主要有：图解法、解析法和试验法。图解法的特点是形象直观，但对于机构的一系列位置进行分析时，需要反复作图，步骤相当繁琐。实验法有赖于试验样机及实验平台的建立。解析法的特点是用数学表达式表示各运动参数的关系，然后求解，可得到较高的精度。对针刺机的运动分析一般采用解析法中的复数矢量法或封闭矢量多边形投影法。本文采用封闭矢量多边形投影法对针刺机构进行运动分析。

图3中，AB为曲柄，BC为连杆。现以主轴中心A为坐标原点，水平方向为X轴建立右手坐标系。按图3标出的各构件矢量方向及其位置角，建立矢量方程及其投影方程：

将矢量方程分别向X、Y轴投影，可得位移方程组如下：

将式（2）对时间求一阶导数可得速度方程组如下：

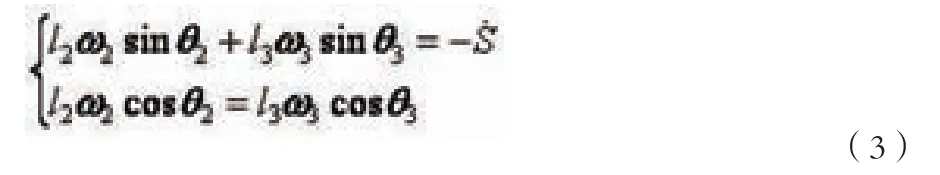
将式（3）对时间求一阶导可得加速度方程组如下：

由于产品的加工是通过针板上的刺针反复针刺来实现的，因此针板的运动参数对产品的加工至关重要，需对针板进行运动分析。上述方程组的求解可在计算机上实现，根据针刺机的工艺要求，偏心距为25mm，针刺动程定为1200次/min，分别对针板的位移、速度和加速度进行分析。

3.1 针板的位移分析

图4 针板的位移曲线

如图4所示，在主轴旋转360°的过程中针板的位移曲线。经过计算，当连杆的长度发生变化时，所得到的位移曲线没有发生任何变化，所以连杆的长度对针板的位移规律没有影响。

3.2 针板的速度分析

首先研究连杆的长度对针板速度的影响，如图5所示，偏心距e=25mm，曲线1为连杆长度为285mm时针板的速度曲线；曲线2为连杆长度为185mm时针板的速度曲线；曲线3为连杆长度为85mm时针板的速度曲线。

图5在偏心距相同连杆长度发生变化的针板速度曲线

由图可以清晰地表明：当机构的偏心距不发生变化时，即使连杆的长度发生明显的改变，对针板运动速度的影响也是比较微弱的。

然后研究偏心距对针板速度的影响，如图6所示，在主轴旋转360°的过程中针板的速度曲线。连杆长度均为285mm。曲线1为偏心距为20mm时针板的速度曲线；曲线2为偏心距为23mm时针板的速度曲线；曲线3为偏心距为25mm时针板的速度曲线。

图6 在连杆长度相同偏心距发生变化的针板速度曲线

由图可以清晰地表明：当机构的连杆不发生变化时，改变机构的曲柄长度，也就是偏心距发生变化时，对针板的运动速度规律的影响是很大的。偏心距越大，针板在极限位置的速度就会越大。

3.3 针板的加速度分析

主要研究连杆长度对针板运动加速度的影响。如图7所示，在主轴旋转360°的过程中针板的加速度曲线。偏心距为e=25mm，曲线1为连杆长度为285mm时针板的加速度曲线；曲线2为连杆长度为185mm时针板的加速度曲线；曲线3为连杆长度为85mm时针板的加速度曲线。

图7 在偏心距相同连杆发生变化的针板加速度曲线

由图7可以清晰地表明：当机构的偏心距不变时，较大程度的改变连杆的尺寸，对针板的加速度曲线是有一定的影响的。连杆的长度越短，针板在高位时的加速度就越小，反而在低位时的加速度会变大，这是该机构比较有特点的地方。这样一来，对针刺工艺的影响就是巨大的，可以提高生产效率并且能够一定程度改善产品的质量，但是加速度的增加使得针刺机构的惯性力和惯性力矩都会相应的增大，从而引起很大的震动和噪声，这就要求在设计的过程中权衡利弊，达到最理想的效果。

4 针刺机构动力学模型建立与仿真

4.1 构件的惯性力和惯性力矩

如图8所示，一般在作平面运动的机构中，运动的构件（匀速运动的除外）会产生一个惯性力）和一个惯性力矩其中分别是运动构件的质量和转动惯量，和分别是运动构件质心的加速度和角加速度。负号说明惯性力的方向与构件加速度方向相反，惯性力矩与质心角加速度的方向相反。但存在以下两种特殊运动状况：当构件绕质心回转时，惯性力为零；直线运动的构件，不产生惯性力矩。

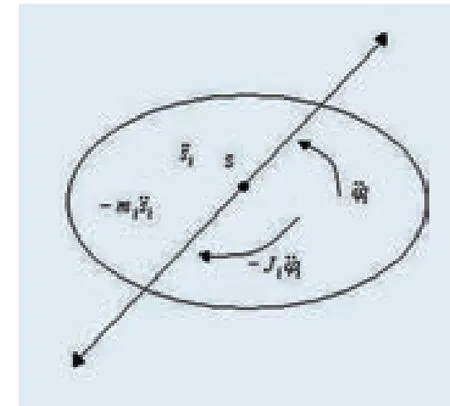
图8构件的惯性力与惯性力矩

3.2 针刺机构动力方程的建立

在本文的动态静力分析中忽略了运动副的摩擦，如图9为针刺机构的直角坐标系，分别为构件1、构件2的质心。将该机构的各构件分离并加上各构件运动副的约束反力、惯性力、输入力矩等。根据求解得出的运动数据，先计算出各构件的惯性力和惯性力矩，再根据达朗伯原理对针刺机构进行动态静力分析。

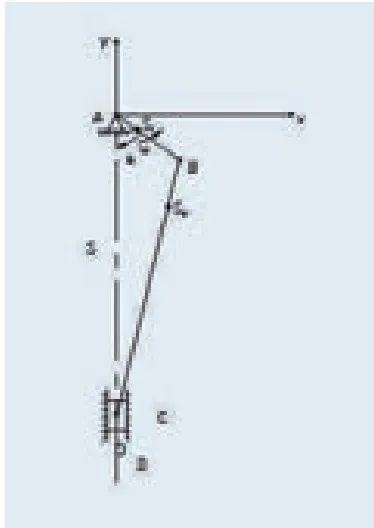
图9 针刺机构的平面简化图

各构件受力情况如图10、图11、图12所示，假设各构件所受外力、力矩、运动副反力均为正方向。列出各构件和力矩的平衡方程：

图10 AB杆受力分析图 图11 BC杆受力分析图 图12 滑块C杆受力分析图

构件1（如图10所示）的力和力矩的平衡方程：

构件2（如图11所示）的力和力矩的平衡方程：

构件3（如图12所示）的力和力矩的平衡方程：

在这三个构件的力和力矩方程中，在构件1上作用平衡力矩Md。平衡力矩的定义：为维持机构原动件按理想的运动规律运动（对原动件做回转运动的机构通常是匀速转动）而需要施加在原动件上的驱动力矩。

在上面的力和力矩平衡方程中，FAx、FBx、Fcx、FDx分别为构件分离后在运动副A、B、C、D在x方向的约束反力。FAy、FBy、FCy、FDy分别为构件分离后在运动副A、B、C、D在y方向的约束反力。F1x、F2x、F3x分别为构件所受外力在x方向的分力。F1y、F2y、F3y分别为构件所受外力在y方→向的分→力。(LS1A→)x、(LS1B→)x、(LS2B) x、(LS2C) x分别为矢量S1A、LS1B、LS2B、LS2C在→x方向的→分量。(L→S1A)y、(LS1→B)y、(LS2B)y、(LS2C)y分别为矢量 LS1A、LS1B、LS2B、LS2C在y方向的分量。m1、m2、m3分别为构件1、构件2、滑块 3 的质 心的质量。S1x、 a˙˙S2x、 a˙˙S3x分 别为构件1、构件2、滑块3的质心加速度在x方向的分量。a˙˙S1y、 a˙˙S2y、 a˙˙S3y分别为构件 1、构件 2、滑块 3 的质心加速度在y方向的分量。J1、J2分别为构件1、构件2的转动惯量。ε1、ε2分别为构件1、构件2的角加速度。Md为作用于曲柄上的平衡力矩。

将以上8个方程组成一个8元线性方程组：

式中：

为未知量，包含了机构各运动副中的反力和作用于原动件的平衡力矩。

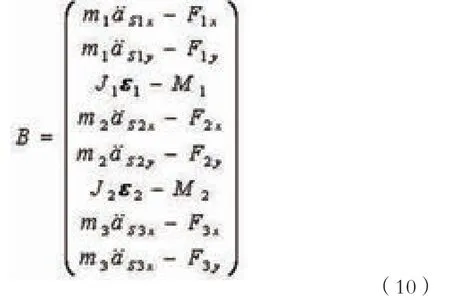
为一8x1的已知列阵，包含了机构所受外力、惯性力和惯性力矩。

为一8x8已知方阵，其元素与构件的质心位置有关。

式（8）就是针刺机构的动态静力分析方程。在完成了机构的运动分析之后，就可以求出机构的位置参数、各构件的角加速度和质心加速度。即可确定列阵B和方阵A。求解这一线性方程组，即可求得列阵X，得到机构的各运动副中的反力和作用于原动件上的平衡力矩。

方阵中的(Ls1A)x、(Ls1B)x、(Ls2B)x、(Ls2C)x、(Ls1A)y、(Ls1B)y、(Ls2B)y、(Ls2c)y是各矢量在坐标轴上的投影，是随着机构位置的不同而变化的；列阵B中除去构件的质量和转动惯量外，其余各量也都是或可能是随着机构位置不同而不变化的量。因此，求解线性方程组（8），只能求解机构在某一位置时的平衡力矩和各运动副中的反力。如果需要求得在机构的一个运动周期中平衡力矩和运动副反力的变化情况，则需要将机构的运动周期离散化，得到机构不同位置，再对多个不同位置分别进行一次运动分析和动态静力分析。

4.3 针刺机构动力学分析

为了求出X，必须知道A和B中的已知量，其中包括各构件的长度、质心位置、质量和转动惯量。初定所有构件的材料为45号钢，ρ=7.85g/cm2。

曲柄（AB杆） 体积：7.989×105mm3

质量：6.272×10-1kg

长度：25mm

质心位置：1.815×10mm转动惯量：0.005N·m2

连杆（BC杆） 体积：8.425×105mm3

质量：6.613×10-1kg

长度：260mm、220mm、180mm

质心位置：1.019×102mm

转动惯量：0.068N·m2

滑块（C） 体积 ：1.853×105mm3

质量：1.846×10-1kg

在工况转速下，主轴转角从0°开始转过360°，求解（3-9），即可得到FAx、FAy和Md。利用下式可以求得A处运动副的约束反力。

当曲柄转速 =1200r/min时，A处约束反力FA随主轴转角θ的变化曲线如图13所示。

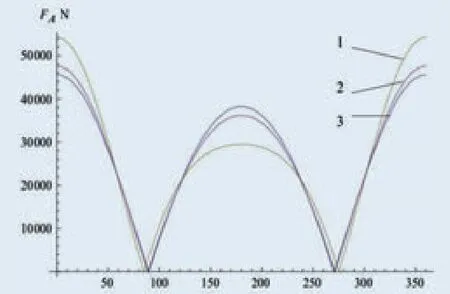
图13 A点约束反力曲线

图13中曲线1、2、3分别为连杆长度为260、220、180mm时A处约束反力FA；由图3可知，偏心距为一定情况下，连杆的长度越短，其机构所受的约束反力就越大；因此，连杆的长度不能太短，一般连杆长度在200～250mm之间为最佳，国外一般取25mm。

由图可以看出，A点的支反力是比较大的。这也表明在主轴和偏心机构上承受着很大的针刺力，因此如果采用两对双曲柄的针刺结构可以有效地改善机械的平衡并且能分担巨大的针刺力，可以有效地保护零部件。

5 结论

（1）当机构的偏心距不变时，较大程度的改变连杆的尺寸，对针板的加速度曲线是有一定的影响的。连杆的长度越短，针板在高位时的加速度就越小，反而在低位时的加速度会变大，这是该机构比较有特点的地方。这样一来，对针刺工艺的影响就是巨大的，可以提高生产效率并且能够一定程度改善产品的质量，但是加速度的增加使得针刺机构的惯性力和惯性力矩都会相应的增大，从而引起很大的震动和噪声，这就要求在设计的过程中权衡利弊，达到最理想的效果。

（2）当偏心距为一定情况下，连杆的长度越短，其机构所受的约束反力就越大；因此，连杆的长度不能太短，一般连杆长度在200～250mm之间为最佳。

[1] 赵宁涛，孙荣禄, 针刺机震动问题研究［J］,非织造布，2009,17(6):43-44.

[2] 鞠永农, 浅谈国产针刺机的开发现状及发展趋势[J], 产业用纺织品，2010,28(1):19-23.

[3] 郭秉臣.非织造布学[M].北京：中国纺织出版社,2002.

[4] 张策.机械动力学[M].北京：高等教育出版社，2006.

[5] 同济大学应用数学系.线性代数[M].北京：高等教育出版社，2001.