增压锅炉锅筒瞬态温度场在线监测

李 斌，史良宵，陈 丰，孙恩慧

(华北电力大学能源动力与机械工程学院，河北保定071003)

0 引言

锅筒是增压锅炉最大的厚壁承压部件，增压锅炉机组经常频繁的启停及变负荷运行，较大的负荷波动会导致锅筒壁温发生剧烈变化，从而会产生交变的热应力［1－3］，给机组运行带来安全隐患，缩短锅筒的使用寿命。温度场计算是应力计算以及疲劳寿命分析的基础，因此对增压锅炉锅筒温度场进行研究，并对其进行在线监测，指导锅炉运行，对于提高机组的安全性、经济性和实行现代化管理具有重要的意义［4，5］。

传统的求解锅筒温度场的方法为导热问题的直接解法(正问题解法)，根据锅筒内部的换热条件，在已知结构参数、热物性参数、初始条件和边界条件的前提下，通过求解导热微分方程得到温度场［6，7］，该方法适用于任意复杂边界条件情况，但是边界条件以及初始条件由于条件限制其系数多采用经验数据或假定［8］，这将影响温度场计算精度。

为了弥补导热正问题求解方法的上述不足，人们提出了温度场计算的导热反问题解法［9－11］。其思想是:在锅筒的外壁布置热电偶测量外壁温度将其作为已知条件，建立控制容积的能量平衡方程，逐步反推求得整个锅筒瞬态温度场。导热反问题解法思路简单，所需网格数量少，计算精度高，已被应用于电站锅炉温度场在线监测系统［12］。

相对于电站锅炉而言，增压锅炉锅筒结构较为复杂，加之其上部区域外壁近似绝热，但底部直接接触炉内火焰，并且两侧夹层区域外壁与维持锅炉炉膛正压的热空气对流换热，因此传热条件比较复杂。复杂的锅筒结构以及炉内高温环境使得导热反问题解法的应用受到了限制。

由于导热正问题能够求解复杂边界锅筒瞬态温度场，在利用其优势的同时，为减弱温度场初始条件以及经验对流换热系数带来的影响，结合增压锅炉外壁受热的特点，最终提出了导热正反问题耦合求解锅筒瞬态温度场的计算方法，充分应用导热正问题、反问题解法各自的优点，求得整个锅筒的瞬态温度分布，提高其温度场的计算精度。

以某增压锅炉冷态启动过程为例，对计算方法进行了说明，并通过数值计算软件Ansys 以及实验数据对该方法的计算结果进行了验证。最终开发了一套锅筒温度场在线监测系统，实时监测锅筒截面温度，并监测测点温度时程曲线以及实现历史数据的查询等功能，达到对锅炉锅筒温度场在线监测、指导运行并管理机组的目的。

1 温度场计算

锅炉锅筒为一个长圆筒形压力容器，锅筒轴线方向上内部工质温度及换热条件变化不大，因此简化为二维问题处理。

1.1 导热正问题解法求解温度场

(1)导热正问题解法

图1 为某增压锅炉锅筒简化模型及其正问题解法网格划分示意图。增压锅炉锅筒内壁换热条件与常规电站锅炉锅筒相同:上部空间为壁面与饱和水蒸气的对流换热，下部空间为壁面与饱和水的对流换热。与常规电站锅炉锅筒区别在于增压锅炉锅筒底部区域外壁所处环境相对复杂:两个深灰色区域外壁与热空气进行对流换热;底部浅灰色填充区域锅筒外壁直接与炉内火焰接触，进行辐射换热;其余部分外壁加装保温层，可近似按绝热处理。

图1 锅筒简化模型及正问题解法网格示意图Fig.1 Simplified model of drum and grid division of direct method

正问题解法基于SIMPLE 算法，采用Fortran语言编制程序，通过求解导热微分方程，得到锅筒的温度场。

二维非稳态常物性无内热源导热微分方程:

边界条件:

绝热边界:

内壁边界:

夹层对流:

辐射传热:初始条件:

上式中各符号说明见表1。

在图1所示的计算区域离散网格内，通过采用控制容积积分法推导出离散方程，将上述导热微分方程以及边界条件进行离散，根据上述理论及公式编制计算程序，然后将离散方程进行迭代求解，求得锅筒瞬态温度场。

(2)导热正问题解法验证

为了验证导热正问题解法程序的精度，利用Ansys 软件对锅炉冷态启动过程锅筒的温度场进行计算。验证时程序采用与Ansys 相同的计算参数，分区域加载边界条件，锅筒计算参数如表1所示。

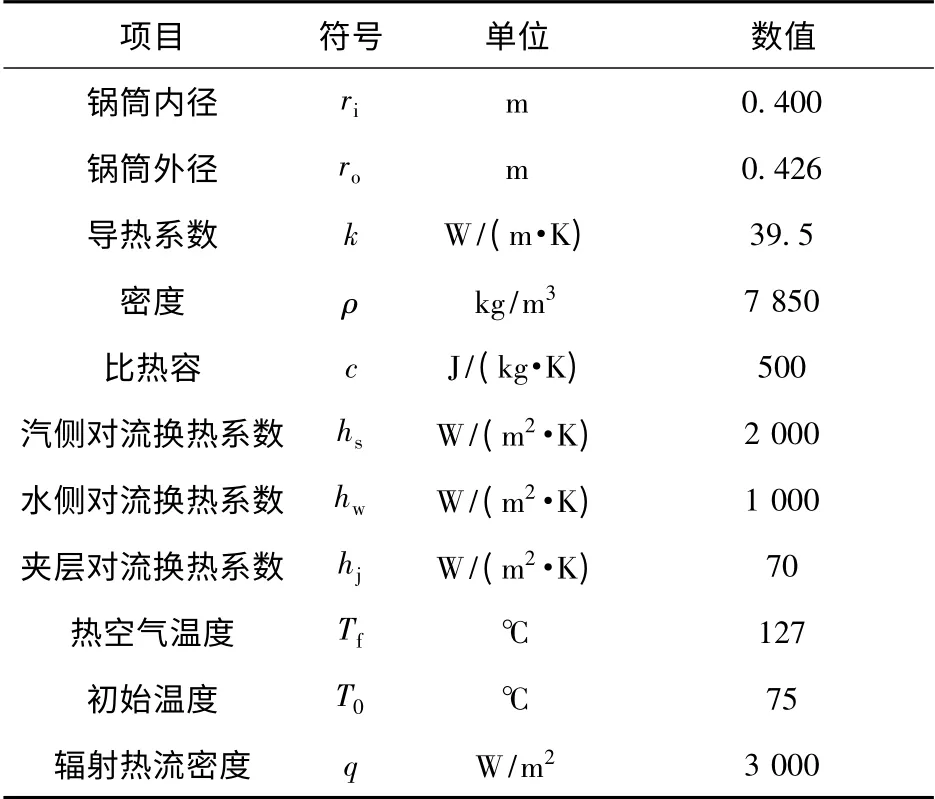
表1 锅筒计算参数Tab.1 The calculated parameters of drum

启动过程锅筒内水(水蒸气)饱和温度T∞随时间的变化如图2所示。

内壁节点18 的正问题解法程序计算温度、Ansys 数值模拟温度与实验测量温度对比结果如图3所示。

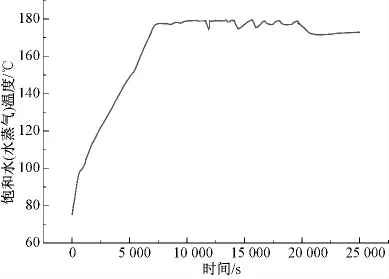
图2 锅筒温度随时间变化曲线Fig.2 The curve of temperature variation of the drum

图3 节点18 温度随时间的变化关系对比曲线Fig.3 Contrast curve of temperature variation with time at node 18

由上图可以发现，程序计算温度与Ansys 模拟结果在整个时程上都非常接近;与实验测量值大部分时间段吻合度较高，因此假定的汽侧对流换热对整个时程来说都比较合理，但在初始800 s 内温度差距都比较大，最大差距达30 ℃左右，这是由于初始时刻，锅筒内壁上部空间没有直接接触给水，温度相对较低，没有达到锅炉上水温度，同时锅炉启动后，给水没有达到饱和温度，使得上部蒸汽相对较少，对流换热相对较弱，显然假定的汽侧对流换热系数不适合这一时间段。因此整个锅筒初始温度假定为锅炉上水温度以及汽侧对流换热系数采用经验系数两部分原因造成了初始阶段上部空间程序计算的内壁温度与实验值偏差较大。

1.2 导热正反问题耦合解法求解温度场

(1)导热正反问题耦合解法

导热反问题不需要已知锅筒内壁对流换热系数和初始温度，仅需知道外层节点的温度就能反推得到整个锅筒的温度，所需节点少，计算精度高［12］。

为了有效的避免导热正问题解法的前述问题，充分的利用导热正反问题各自的优势，结合锅筒外壁受热的结构特点，将锅筒截面划分为外壁不受热区(温度场采用导热反问题解法求解)和外壁受热区(温度场采用导热正问题解法求解)，图4 为其截面区域划分示意图。

(1)导热反问题解法

反问题求解区域局部网格示意如图5所示，沿径向划分为3 层(实线)，为方便公式描述，图中对节点进行了简单编号，并且用虚线标出节点所代表的控制容积。

通过热电偶在外壁节点处测量温度值，然后对节点代表的控制容积列写能量守恒方程式，反推求得该区域的温度场。

图5 反问题解法局部网格示意图Fig.5 Local grid division of inverse method

其中节点13、14、15 的能量守恒表达式如下:

式中:Δφ 为容积角度变化量，rad;Δr 为容积径向变化量，m;Ti为i 节点温度，℃;qi为i 节点处的热流密度，W/m2;r1为内径ri，m;r2，r3，r4分别为中间各层半径，m;r5为外径ro，m。

联立求解上述方程可得中间层节点7、8、9 的温度。同理，对中间层节点8 列能量守恒表达式，最终解得内层节点3 的温度:

根据外层节点的温度，可逐次内推求得内层节点的温度。改变不同外层节点位置，相应的得到整个反问题求解区域内层节点温度，进而得到锅筒横截面反问题解法求解区域的瞬态温度场。

(2)导热正反问题耦合解法

结合锅筒的结构特点，分区域分别采用两种方法对不同的离散区域进行单独的温度场求解。

首先根据已知的反问题求解区域外壁的温度值(热电偶测温)，采用反问题方法求解该区域的锅筒温度场。为实现正问题求解区域边界条件的封闭，两区域交接处(耦合边界S1，S2)采用导热问题正反耦合，将反问题解法求得的交界处的温度值通过插值的方式赋值给正问题解法，作为已知条件(第一类边界条件)，这样就完成了两个求解区域的温度传递。然后在已知结构参数、热物性参数、初始条件和其他边界条件的前提下，解得正问题求解区域的温度场，因此实现导热正反问题耦合求解。

利用上述理论及公式，采用C + +和Fortran进行混合编程，得到导热正反问题耦合解法程序，实现耦合求解功能。

1.2.2 导热正反问题耦合解法验证

验证方法为:导热反问题求解区域外壁温度值为锅筒外壁测量数据，导热正问题求解区域的边界条件按表1 给定边界条件进行加载，然后用导热正反问题耦合解法程序求解锅筒温度场。最后将程序计算结果与1.1(2)节Ansys 数值模拟结果以及实验数据进行比较分析。

图6 为反问题解法区域内壁节点18 温度值对比。由图6 与图3 对比可知，导热正反问题耦合解法在节点18 处具有较高的计算精度，很好的避免了温度场初始化以及由假设对流换热系数带来的计算误差。

图6 节点18 温度随时间的变化关系对比曲线Fig.6 Contrast curve of temperature variation with time at node 18

图7 为节点19 的温度值对比。节点19 代表正问题解法区域汽空间处的内壁温度。由图7 可以看出:与图3 中18 节点相比，锅炉启动初期的初始温度和汽侧对流换热系数对节点19 温度值影响较小，整个计算时程三者温度值具有较高的吻合度，因此表明该区域的边界条件及初始条件比较合理。

图7 节点19 温度随时间的变化关系对比曲线Fig.7 Contrast curve of temperature variation with time at node 19

图8、9 分别为节点20、21 的温度值对比。节点20 代表正问题解法底部辐射区域内壁温度，节点21 代表正问题解法夹层对流换热区域内壁温度。从图8 可以看出实验测量数据存在小范围波动，这是由于节点20 处于上升管与锅筒连接区域附近，由于工况复杂，给水温度不稳定。但由整体可知，正问题解法的各边界条件处理基本合理，计算结果与实验测量结果吻合度较高。

图8 节点20 温度随时间的变化关系对比曲线Fig.8 Contrast curve of temperature variation with time at node 20

第6 500 s锅筒截面沿圆周方向程序计算内外壁温度与实验内壁测量温度对比关系如图10所示。从图中可以看出二者内壁温度吻合度较高。0～90°区间，启动过程中上部汽空间由于内壁面温度较饱和蒸汽温度低，蒸汽凝结，释放大量汽化潜热，相对于下部水空间而言换热系数大，内外壁温度偏高;汽水交界面附近温度逐渐由汽空间过渡到水空间;120°～135°与240°～250°两夹层区域由于此刻外壁温度高于热空气温度，二者进行对流换热，导致外壁温度有明显降低趋势;底部辐射区域外壁由于受到热流作用，导致温度上升比较明显，并且外壁温度高于内壁温度。

图9 节点21 温度随时间的变化关系对比曲线Fig.9 Contrast curve of temperature variation with time at node 21

由于外壁结构限制及其部分区域换热的影响，影响热电偶布置，因此缺少正问题求解区域实测外壁数据，但是内壁温度吻合较好，间接表明外壁给定边界条件合理，程序计算结果与实际情况较符合。

图10 锅筒截面圆周方向内外壁温度变化曲线Fig.10 The curve of temperature variation along the circumferential direction at internal and outer of the drum

由图6～图10 对比可知，导热正反问题耦合解法计算温度场在时程与空间角度都与实测数据高度吻合，区域划分以及各边界条件处理比较合理，因此表明正反导热问题耦合解法在复杂边界条件下具有很好的适应性与可行性。

2 温度场在线监测系统的开发

后台程序总体分为反问题解法、正问题解法两个模块，通过编制相关求解程序，并完成各模块之间相互衔接，实现计算过程的程序化，形成完整的软件系统，实现温度场耦合求解计算功能。现场采集过来的外壁测点数据通过OPC 协议端口传输到后台进行计算，后台程序运行结果保留在相应的ORACLE 数据库中;前台采用相关的组态工具，制作相关前台显示功能界面，数据显示采用Borland C+ +Builder 与数据库实现动态链接，将求解的整个锅筒和危险点的温度实时显示，实现整个运行过程的在线监测［13］。

在线监测系统作用主要表现为:

(1)在线采集并存储测点的温度、压力，水位等数据;

(2)在线计算并生成和显示测点的温度以及时程曲线;

(3)在线计算和分析被测点的温差，并判断是否超限并进行报警;

(4)通过人机对话方便迅速地实现历史数据以及图形的查询和显示。

在线监测系统计算流程如图11所示。

图11 在线监测系统计算流程图Fig.11 The calculation flow chart of online monitoring system

图12 为系统绘制的10 000 s 时刻的锅筒截面等温线示意图。该时刻上部空间温度相对平稳，温差较小;夹层对流换热区域由于外壁温度高于热空气温度，对外放热，导致该区域温度下降;底部辐射区域由于热流作用，导致外壁温度高于内壁温度。

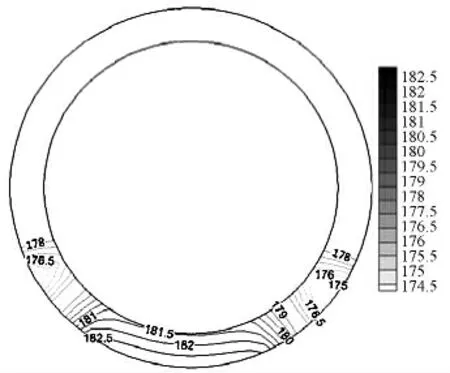
图12 锅筒截面等温线示意图Fig.12 Isotherm schematic of drum sectional

3 结论

(1)根据增压锅炉锅筒复杂的外壁结构及其外壁受热特点，提出了导热正反问题耦合求解的方法对锅筒进行瞬态温度分析，将两种受热情况和计算方法同时应用于一个元件上，充分利用两种解法的优势，克服了单一解法的缺陷与不足。

(2)通过与Ansys 数值模拟以及实验测量数据进行对比，验证了导热正反问题耦合解法在复杂边界条件下具有很好的适应性与可行性，得到具有较高精度的温度场，为接下来的应力分析打基础。

(3)通过锅筒温度场在线监测系统的开发，指导实际运行，规范锅炉启停操作，有效避免超温对锅筒带来的寿命损耗，提高实际运行过程中的安全性和可靠性。

［1］商福民，吕邦泰，庞立平.锅炉汽包壁上下温差热应力有限元分析［J］.华北电力大学学报，1999，26 (1):52－56.

［2］田乾.电站锅炉汽包的应力分析及疲劳可靠性计算［D］.北京:北京化工大学，2013.

［3］李斌，陈听宽，沈月芬.基于有限元方法的锅炉汽包应力在线监测程序的研究［J］.西安交通大学学报，2003，37 (5):447－450.

［4］李立人，陈玮，盛建国，等.锅炉受压元件的高温蠕变－ 疲劳寿命设计计算方法［J］.动力工程，2009，29 (5):409－416.

［5］刘彤，徐钢，庞力平，等.锅炉炉内承压部件的蠕变分析及寿命计算［J］.动力工程，2004，24(5):631－635.

［6］陶文铨.数值传热学(第2 版)［M］.西安:西安交通大学出版社，2001.

［7］赵铁成，沈月芬，朱国桢，等.电站锅炉锅筒温度场计算——三维非稳态变物性材料不均匀导热问题有限元分析［J］.中国电机工程学报，1997，17(4):217－220.

［8］段鹏，周新雅，杨菁，等.锅炉汽包复杂应力状态及低周疲劳寿命研究［J］.热力发电，2010，39(8):28－32.

［9］Cebula A，Taler J.Determination of transient temperature and heat flux on the surface of a reactor control rod based on temperature measurements at the interior points［J］.Applied Thermal Engineering，2014，63 (1):158－169.

［10］Hào D N，Thanh P X，Lesnic D.Determination of the heat transfer coefficients in transient heat conduction［J］.Inverse Problems，2013，29 (9):95020－95040.

［11］Hu W S，Li B，Cao Z D，et al.An Inverse Method for Online Stress Monitoring and Fatigue Life Analysis of Boiler Drums［J］.Journal of Chongqing University，2009，8 (2):89－96.

［12］李斌，陈丰，史良宵.锅炉汽包瞬态温度场在线监测［J］.动力工程学报，2014，34 (9):714－719.

［13］匡江红，杨庆娣.电站锅炉过热器壁温在线监测系统的开发研制［J］.电力科学与工程，2004，(2):66－68.