分离压对不同基底上含活性剂液滴铺展特征的影响

杨保才，叶学民，李春曦

(华北电力大学能源动力与机械工程学院，河北保定071003)

0 引言

薄液膜在基底表面上流动展现出丰富的动力学特征，如表面波形态、去湿结构、接触线等，其在汽车涂膜，数字储存设备制造，传热传质等方面具有广泛的应用［1－2］。不同外力驱动下液膜的流动行为一直是流体力学领域研究的热点问题。驱动力可以是热毛细力、重力、离心力、电场力等，当液膜或液滴中含有表面活性剂时，驱动力也可以是由浓度梯度引起的Marangoni 效应，其在生物、航空航天及化工等领域发挥着至关重要的作用［3－4］。

对于非平整壁面上液膜的流动现象，近年来得到广泛关注。文献［5］研究了流经连续矩形基底的液膜形态，分析了重力、惯性力及基底高度对液膜流动的影响。文献［6］模拟了底部均匀加热的波状基底上液膜的流动行为，研究表明处于基底波峰处的液体逐渐向波谷处流动，最终液膜发生破断，而加入分离压可有效阻止液膜破断现象。文献［7］建立了沟槽表面液滴在剪切气流下脱落的力学模型，表明液滴脱落所需要的风速随沟槽尺寸增大而提高。文献［8］对波状基底上的液滴铺展加入活性剂影响，发现液膜在基底凹处形成明显的去润湿现象。

分离压是影响液膜流动行为的重要因素之一，当液膜厚度处于微纳级时，其流动特性会受到包括周围液体分子和固液分子间的范德华引力、双电层斥力和短程结构斥力等作用力的影响［9－10］，文献［11］在研究超薄液膜的去润湿现象时，引入分离压模型，发现分离压中的范德华引力是导致液膜失稳，形成破断或去润湿结构的直接诱因。文献［12］研究了带有电荷的活性剂液滴的铺展行为，并分析了双电层斥力对铺展过程的影响。文献［10、13］建立了包含范德华力、Born 斥力和静电斥力的分离压模型，并采用非模态理论对含活性剂液膜去润湿现象进行了稳定性分析。

实际应用中，液滴多为在非平整壁面上铺展，且壁面结构的多样性和复杂程度将在不同程度上影响液滴的铺展过程;而且，当铺展液膜厚度处于分离压作用范围时，分离压作用不容忽视，基底作用与分离压作用结合势必对液滴产生独特的铺展特征。而同时考虑表面活性剂、分离压及不同基底结构对液滴的铺展影响，目前尚未有报道。本文根据润滑理论［14－15］，通过引入受活性剂影响的分离压模型，借助数值模拟研究表面活性剂、分离压及基底结构耦合作用下液滴独特的铺展行为。

1 理论模型及演化方程组

1.1 液滴铺展物理模型

如图1所示，D*为基底高度，在函数为s*(x*)的基底上预置一层厚度为Hb

*－s*(x*)液膜，初始时刻将一滴含不溶性活性剂的液滴放置在此液膜上，则液滴在活性剂浓度、基底和分离压的共同作用下铺展。假设活性剂液滴为不可压缩牛顿流体，动力黏度μ*和密度ρ*均为常数，基底壁面无滑移、无渗透，忽略气体黏性影响。液滴最大高度H*与流动方向尺度L*相比非常小，即满足∈=H*/L*《1，符合润滑理论［14－15］。(上标“*”代表有量纲量)

图1 非平整壁面上含不溶性活性剂液滴的铺展示意图Fig.1 Schematic diagram of the spreading of liquid droplet with insoluble surfactants on uneven topography.

1.2 演化模型的建立

对于不可压缩、粘性牛顿流体的活性剂溶液铺展过程，其控制方程包括连续性方程、运动方程和浓度输运方程。边界条件包括壁面上的无滑移、无渗透条件及接触界面上的法向和切向应力平衡方程。

无量纲的连续性方程、运动方程及浓度输运方程为

表面张力关系式为

无量纲边界条件为

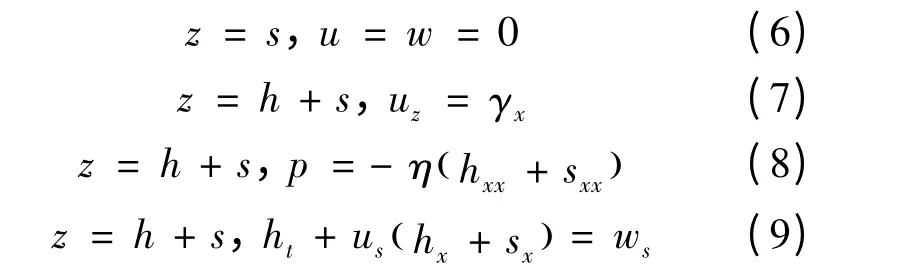
分离压Λ 采用与文献［11］所提模型类似的形式

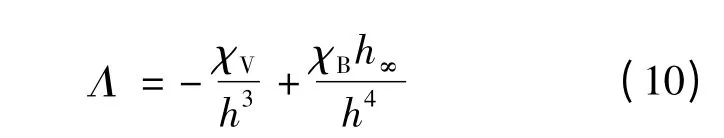
本文所建模型不同之处在于，χV和χB均为与活性剂浓度有关的线性函数。即χV=1 +α1Σ，χB=1 +α2Σ，其中α1、α2表征与活性剂浓度关联系数，如无特殊说明α1=α2=1。本文采用该模型分析含活性剂液滴在不同结构壁面上的铺展动力学特征。

结合式(1)～(10)，通过积分可得液膜高度h和活性剂浓度Σ的演化方程组:

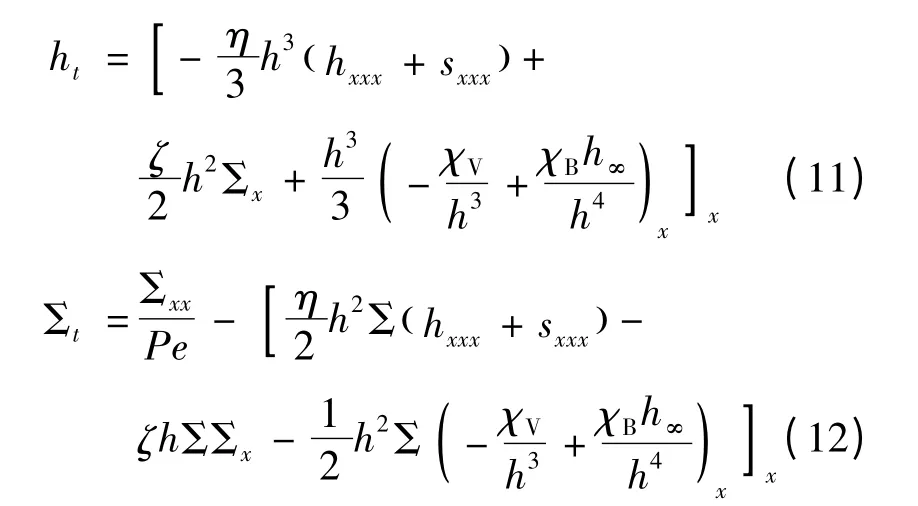
式(11)～(12)即为受分离压作用、含不溶性活性剂溶液非均匀铺展理论模型。上式中包含ζ、η 和Λ 的项分别代表Marangoni 效应、毛细力和分离压对h 和Σ演化的贡献，通过求解该方程组可获得液滴铺展特征。

2 数值模拟及结果分析

2.1 初始条件及边界条件

采用PDECOL 程序［12，18］求解演化方程式(11)和式(12)。根据演化尺度选取0 ＜x ＜15 一维区域进行计算，模拟中将其划分为2 000 个均匀网格，与网格数3 000 相比，计算误差仅降低0.06%，满足计算精度要求。

初始液膜高度和活性剂浓度分布为

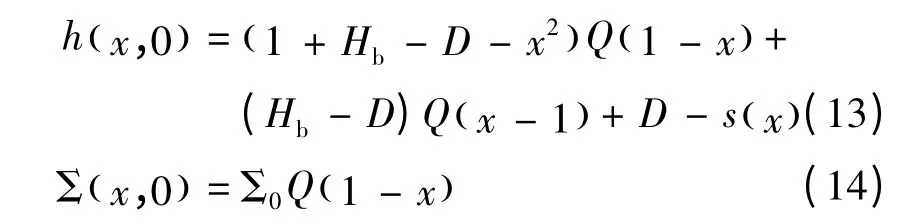
式中:Q(x)= 0.5［1 + tanh(100x)］为海氏阶跃函数。其中，预置液膜高度Hb=0.3;初始活性剂浓度Σ0=1。

液滴铺展过程中保证活性剂摩尔总量守恒，即

壁面函数s(x)为x 的任意函数，通过改变s(x)就可以得到不同的表面特征。本文采用凹槽状、锯齿状、三角状、梯形状和余弦状来讨论不同基底结构对液滴铺展特征的影响。

凹槽状基底函数为

式中:凹槽深度D=0.2;斜度δ=0.1;宽度w=2。锯齿状基底函数为

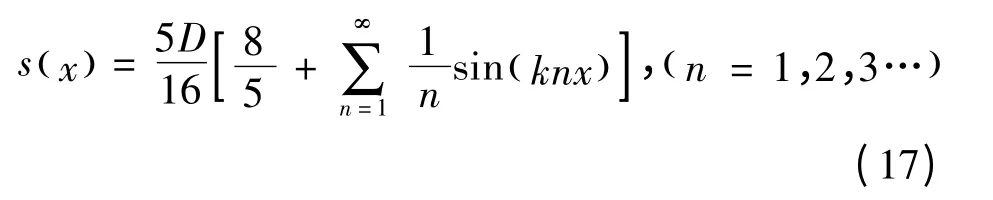
三角状基底函数为

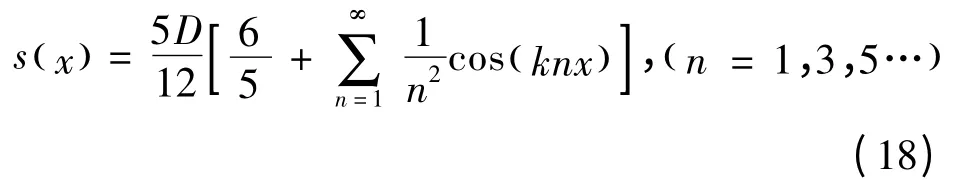
梯形状基底函数为

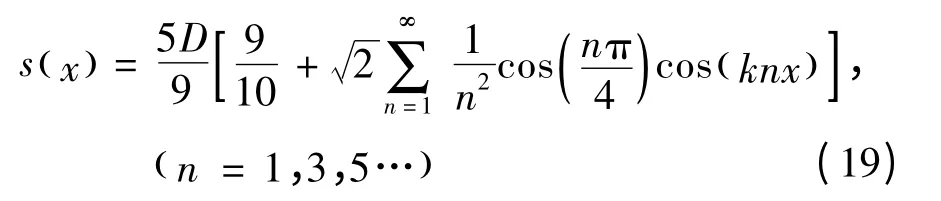
余弦状基底函数为

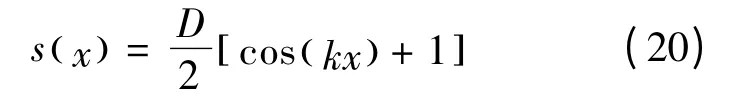
式(16)～(20)中，基底高度D =0.2，基底波数k=2。

2.2 结果分析

为比较分离压作用的影响，首先给出不考虑分离压时的演化特征。图2 为Λ =0 时不同结构基底上液膜高度和活性剂浓度的演化过程。由图可知，总体上各基底上液膜高度演化趋势相同，随时间持续，液滴中心高度下降，铺展前沿附近衍生出不规则的子波结构。随时间延续子波数量增加，同时受基底和活性剂影响波谷附近液膜产生凹陷，而基底驼峰处液膜产生隆起。但与文献［5］不考虑活性剂影响相比，其凹陷深度与隆起高度均增大。这与文献［19］得出的活性剂加剧液膜表面变形程度结论一致。

液滴在不同结构基底上铺展，液膜表面形态不同之处主要表现在基底波峰和波谷处。图2(a)和2(c)表明，最小液膜高度集中在基底第一波谷处，这是由于液滴铺展半径(此处活性剂浓度梯度最大)处于基底第一波谷处，Marangoni 效应明显，液体更快地向下游扩散;同时受基底波谷影响，液体局部压力减小，流速增大，液膜产生凹陷［5，8］。两种作用叠加使第一波谷处液膜高度急剧下降，甚至紧贴壁面，加速诱发去润湿现象的发生［8］。而图2(e)、2(h)、2(g)表明，t=1 时液滴铺展半径处于基底第一波谷附近，此时受到波谷作用明显，液膜高度较低;随时间持续，液滴铺展半径前移且逐渐受到基底波峰作用，液膜高度增大，最小液膜高度则移动至第二波谷处。而比较基底波峰处液膜高度可知，锯齿状液膜高度最大，这是因为锯齿状波峰处曲率较大，引起的压力增长明显。文献［5，8］指出基底表面不平整越大，液膜变形越明显。本文亦得出相同结论。

由活性剂浓度示意图可知，随铺展范围增大活性剂浓度不断降低，但由于受粘性迟滞作用，液滴中心处活性剂浓度扩散较慢，浓度剖面近似于“平台状”。而受基底表面曲率影响基底波谷处液膜高度较小，对应的活性剂浓度梯度较大，而波峰处液膜高度较大，活性剂浓度梯度较小;造成铺展前沿附近活性剂浓度剖面呈现波动特征，这与平整基底上的浓度演化历程有所不同。

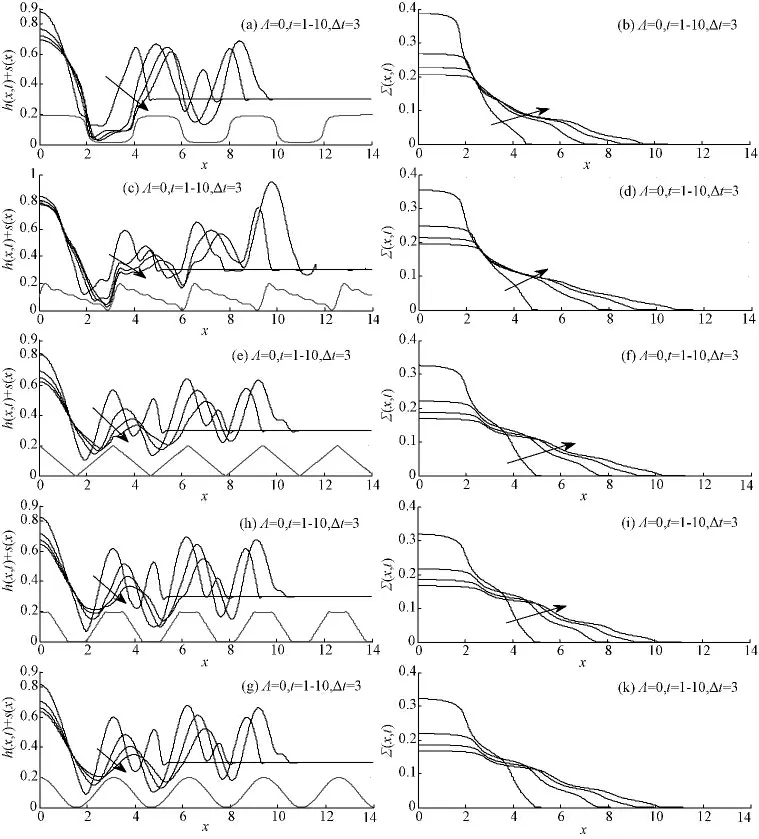
图2 Λ=0 时( a，b) 凹槽状、( c，d) 锯齿状、( e，f) 三角状、( h，i) 梯形状、( g，k) 余弦状表面液膜高度和活性剂浓度的演化历程Fig.2 Evolutions of the film height and surfactant concentration on ( a，b) consecutive trench，( c，d) sawtooth，( e，f) triangular，( h，i) trapezoidal and ( g，k) cosine wave surfaces at Λ=0.

当考虑分离压作用(Λ ≠0)时，液滴的演化时间缩小至t=1。其演化过程如图3所示(如无特殊说明α1=1，α2=1)。受分离压影响，铺展前沿附近衍生出的不规则子波结构明显减少，铺展后期液膜高度整体呈类基底形状变化。形成与Λ =0 时截然不同的演化特征。与Λ =0 时对比可知，分离压作用下，基底波峰处液膜高度下降，波谷处液膜高度上升，尤其图3(a)、3(b)基底第一波谷处液膜高度不再紧贴壁面，去润湿现象消失。说明分离压抑制活性剂及基底影响，使液膜变形程度减缓，铺展更加稳定。文献［20］在分析分离压对平整壁面上液滴铺展影响时，指出分离压作用下液滴半径处并未形成明显的去润湿特征。液滴演化稳定性增强，本文亦得出相同结论。

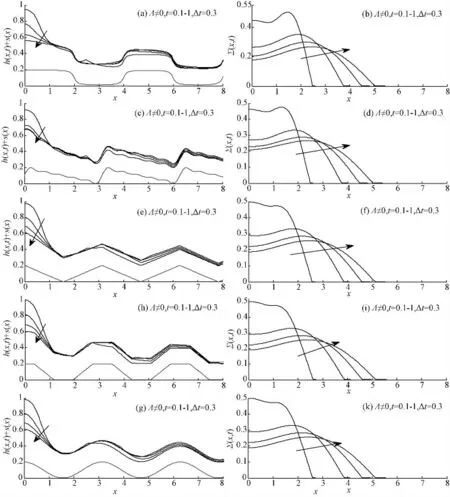
图3 Λ ≠0 ( a，b) 凹槽状、( c，d) 锯齿状、( e，f) 三角状、( h，i) 梯形状、( g，k) 余弦状表面液膜高度和活性剂浓度的演化历程Fig.3 Evolutions of the film height and surfactant concentration on ( a，b) consecutive trench，( c，d) sawtooth，( e，f) triangular，( h，i) trapezoidal and ( g，k) cosine wave surfaces at Λ≠0.

由活性剂浓度示意图可知，分离压作用下，液滴中心活性剂浓度扩散速率加快，进而形成凹陷。随时间延续，凹陷程度加剧且逐渐向下游扩展，表明分离压有助于缓解粘性迟滞作用，从而促进液滴铺展。而与Λ=0 时相比，铺展前沿附近浓度剖面波动特征消失，液滴铺展更加稳定。

为对比分离压对液滴在不同基底上液滴铺展的影响，图4 给出了t=1 时，Λ=0 和Λ≠0 时铺展前沿半径Xf和液滴中心高度Hm随时间的演化行为。图4(a)表明，Λ =0 时凹槽状基底Xf增长速率最小为t0.26，锯齿状基底为t0.27，梯形状、余弦状和三角状基底增长速率近似相等分别为t0.28、t0.283和t0.285但均大于凹槽状和锯齿状的增长率。由图4(b)可知，Hm随时间持续整体呈下降趋势。其中凹槽状下降速率较慢为t－0.08，锯齿状下降速率稍快为t－0.086，梯形状、余弦状和三角状基底下降速率进一步加快，Hm符合关系t－0.09、t－0.092和t－0.094。

Λ≠0 时(α1=1，α2=1)Xf变化趋势与Λ =0时相同，但增长速率明显加快。其中凹槽状基底较为明显为t0.29，快于锯齿状的t0.286，而梯形状、余弦状和三角状增长速率相等为t0.305，均大于Λ =0时相应的增长率。Λ≠0 时Hm变化与Λ =0 时有所不同，其中，凹槽状变化最为明显，其下降速率由Λ=0 时t－0.08加快为Λ≠0 时的t－0.16，梯形状、余弦状和三角状Hm下降速率加快为t－0.14，快于锯齿状的t－0.12。说明分离压作用下液滴铺展速率加快。

3 结论

不计及分离压时，随时间延续，液滴铺展前沿处开始衍生出不规则子波。铺展半径处最小液膜高度持续降低，诱发去润湿现象发生。不平整度越大基底表面上液膜变形越明显。

分离压作用下液滴在不同结构基底上铺展时，液膜高度整体呈类基底形状变化。与Λ=0 时相比，铺展前沿处子波结构明显减少，而铺展半径处最小液膜高度显著增加，相对Λ=0 时铺展更加稳定。分离压具有抑制液膜变形和促进液滴铺展的作用。

分离压作用下铺展前沿半径Xf增长速率提高，液滴中心高度Hm下降速率加快。分离压对凹槽基底液滴铺展促进作用最为明显。

［1］Matar O K，Sisoev G M，Lawrence C J.Thin film flow over spinning discs:The effect of surface topography and flow rate modulation［J］.Chemical Engineering Science，2008，63 (8):2225－2232.

［2］Sawa N，Pavliotis G A，Kalliadasis S.Contact lines over random topographical substrates.Part 1.Statics［J］.Journal of Fluid Mechanics，2011，672:358－383.

［3］李春曦，郭娜，叶学民，等.界面热效应下可溶性活性剂覆展过程的演化模型［J］.华北电力大学学报，2009，36 (2):58－63.

［4］叶学民，姜凯，李春曦.含胶束结构的活性剂溶液非均匀铺展演化模型研究［J］.华北电力大学学报，2012，39 (3):88－93.

［5］Pak M I，Hu G H.Numerical investigations on vortical structures of viscous film flows along periodic rectangular corrugations［J］.International Journal of Multiphase Flow，2011，37 (5):369－379.

［6］Saprykin S，Trevelyan P M J，Koopmans R J，et al.Free-surface thin-film flows over uniformly heated topography［J］.Physical Review E，2007，75 (2):026306.

［7］黄苏和，胡海豹，陈立斌，等.剪切气流驱动下微沟槽表面液滴受力分析［J］.上海交通大学学报，2014，48(2):260－264.

［8］李春曦，裴建军，叶学民.波纹状基底上含不溶性活性剂液滴的铺展过程［J］.化工学报，2013，64(9):3308－3316.

［9］叶学民，李春曦，曹罕，等.表面活性剂溶液铺展过程中的分离压特性［J］.电力科学与工程，2012，28 (5):21－27.

［10］叶学民，沈雷，李春曦.分离压对含活性剂液膜流去湿过程的影响［J］.西安交通大学学报，2013，47(3):96－101.

［11］Warner M R E，Craster R V，Matar O K.Dewetting of ultrathin surfactant-covered films［J］.Physics of Fluids，2002，14 (11):4040－4054.

［12］Zhang Y L，Craster R V，Matar O K.Surfactant driven flow overlying a hydrophobic epithelium:film rupture in the presence of slip［J］.Journal of Colloid and Interface Science，2003，264 (1):160－175.

［13］李春曦，姜凯，叶学民.含活性剂液膜去润湿演化的稳定性特征［J］.物理学报，2013，62 (23):1－10.

［14］赵亚溥.表面与界面物理力学［M］.北京:科学出版社，2012:185－186.

［15］Bhakta A，Ruckenstein E.Decay of standing foams:drainage，coalescence and collapse［J］.Advances in Colloid and Interface Science，1997，70 (1):1－124.

［16］Danov K D，Ivanov I B，Ananthapadmanabhan K P，et al.Disjoining pressure of thin films stabilized by nonionic surfactants［J］.Advances in Colloid and Interface Science，2006，128－130:185－215.

［17］Stubenrauch C，Schlarmann J，Strey R.A disjoining pressure study of n-dodecyl－β－D-maltoside foam films［J］.Chem.Phys，2002，4 (18):4504－4513.

［18］Akyurtlu A，Akyurtlu J F，Denison K S，et al.Application of the general purpose collocation software，PDECOL，to the Graetz problem［J］.Computers and chemical engineering，1986，10 (3):213－222.

［19］Pozrikidis C.Effect of surfactants on film flow down a periodic wall［J］.Journal of Fluid Mechanics，2003，496:105－127.

［20］叶学民，姜凯，李春曦.分离压结合压作用下的活性剂液滴演化特征［J］.化工学报，2013，64 (10):3581－3589.