摇摆参数对自然循环下波谷型脉动的影响
张晓玉,谭思超,*,余志庭,宋禹林,张 虹
(1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨 150001;2.中国核动力研究设计院核反应堆系统设计技术重点实验室,四川成都 610041)
摇摆参数对自然循环下波谷型脉动的影响
张晓玉1,谭思超1,*,余志庭1,宋禹林1,张 虹2
(1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨 150001;2.中国核动力研究设计院核反应堆系统设计技术重点实验室,四川成都 610041)
针对摇摆条件下自然循环波谷型脉动进行研究,构建了计算波谷型脉动的模型并进行了分析,计算结果和实验值符合较好。分析结果表明:对于摇摆运动下的波谷型脉动,在其整体流动波动过程中起主导作用的是摇摆运动引起的附加压降,而在波谷附近,由于产汽的影响,局部摩擦压降和重位压降交替主导流动,并最终诱发波谷处的流动不稳定性;摇摆振幅和频率越大,即摇摆程度越剧烈时,摇摆附加压降波动越剧烈,流量、壁温等热工参数变化越剧烈,波谷型脉动起始点对应功率也越低。
摇摆运动;自然循环;波谷型脉动;流动不稳定性
在海洋条件下行驶的核动力船舶,受海洋条件影响,其冷却剂系统会产生附加加速度和附加惯性力,进而影响核动力系统的热工水力特性和其正常工作状态[1-2]。对于自然循环系统,摇摆运动不仅改变了有效高度,而且由于驱动压头较小,摇摆附加力在整个驱动力中所占比例较大,因此摇摆条件下,自然循环较强迫循环受海洋条件的影响大。
目前,国内外对于摇摆条件下的自然循环系统进行了许多研究,如杨钰[3-4]、Murata[5]、谭思超[6]、郭赟[7]等,相关研究表明,稳态条件下的不稳定性是由热工参数之间的耦合引起的流量漂移或流量脉动;而摇摆条件下,在热工参数耦合脉动之前,摇摆附加力就会使系统产生流量波动。波谷型脉动是一种典型的海洋条件诱发的流动不稳定性。谭思超等[8]对摇摆条件下的波谷型脉动进行了研究,但对其机理的定量分析尚不充分,对于摇摆参数对波谷型脉动的影响分析也不明确。因此,有必要针对摇摆条件对于波谷型脉动的影响展开研究。本文在前期实验研究基础上,构建相关的理论模型,研究摇摆参数对波谷型脉动的影响规律和影响机理。
1 波谷型脉动的特性及其计算模型
1.1 波谷型脉动计算模型介绍
摇摆对系统的附加力会使系统产生与摇摆周期一致的周期性流量波动,一定加热功率下,可在波谷点观察到大量汽泡快速产生,实验段压降急剧增加,形成两相流动不稳定性[8],即波谷型脉动。
图1示出了实验时波谷型脉动发生前后流量的变化,可看出,脉动发生后,波谷流量降低,波峰流量有所升高,波谷附近流量的斜率较脉动前变大,且上升段斜率较下降段斜率大,流量波动曲线对称性变差。同时,发生脉动后加热段出口气泡大量产生并急速通过,引起实验段压降急剧升高。
分析波谷型脉动需要确定产汽点,由实验数据可知产汽时流体欠热,把摇摆条件下的参数代入稳态条件下计算欠热沸腾的经验关系式,其结果和实验数据严重不符,从理论上分析瞬态流动下的产汽点又有一定难度,所以本文在实验研究的基础上拟合了净蒸汽产生点的功率Pnvg的经验关系式(式(1))。式(1)综合考虑了平均流量和最低流量对产汽点的影响,以最低流量和平均流量下流体达到饱和所需功率Pmi和Pave作为参考量。由式(1)可知,平均流量和最低流量越大,产汽点对应功率越大。
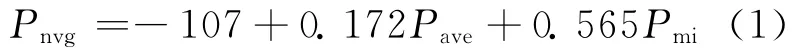
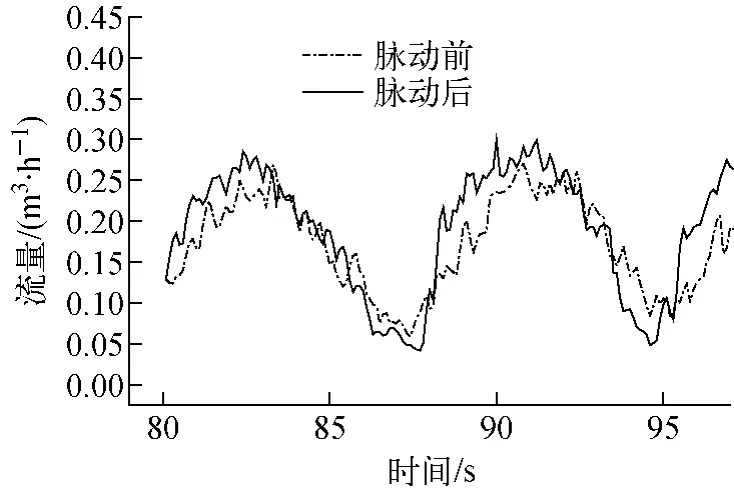
图1 波谷型脉动前后流量的变化(实验值)Fig.1 Comparison of flow rates before and after trough fluctuation(experimental results)
计算波谷型脉动起始点时,在产汽点基础上逐渐增加功率,加热段出口的产汽量会随着功率的增大而逐渐增多,当功率增大到一定值时,出口大量产汽并引起压降的急剧增加,当压降到达一定值时,认为该功率为波谷型脉动起始点所对应功率。刚开始产汽时,流动阻力的影响大于驱动力的影响,所以流量会较产汽之前下降。
在计算产汽点时,之所以拟合式(1)这样一个公式主要是考虑了入口过冷度和流量的影响,经过对实验数据的比较,发现产汽点功率和入口过冷度、流量有很大关系,流量越大,入口过冷度越大,所对应的产汽点功率和波谷型脉动的功率也越大,拟合公式中用到的两个功率综合考虑了它们的影响,与实验值进行对比,效果较好。式(1)是基于本实验系统和实验数据拟合而得,考虑到实验系统的差异,不适宜应用到其他系统上,但从效果看,式(1)的形式具有推广价值。
计算中,给定相关条件,按单相流动模型计算,根据算出的平均流量和最低流量计算Pnvg。当加热功率P超过Pnvg时,则认为实验段出口开始产汽,转入两相计算。
由实验数据可知产汽点功率和脉动起始点的功率相差不超过15%,所以假定实时功率与产汽点功率的差值全部用来产汽,并以波谷处实时流量为定性流量来计算出口状态,如干度和含汽率等。由于产汽时间较短,且沸腾只出现在加热段出口附近,在计算阻力和密度时,假定加热段内不存在两相流动,仅考虑上升段为两相流动。把实验系统分成多段,如加热段、上升段、冷凝段、预热段等。在计算过程中,再把每一段分成多个控制体[9],假定每个控制体的热工参数集中在控制体中心,计算过程中,阻力系数和换热系数与稳态时有所不同,在计算这两个量时用到了考虑摇摆影响的经验关系式[10]。
采用四阶龙格库塔法进行计算,并用C#语言编制程序。计算流程如图2所示。
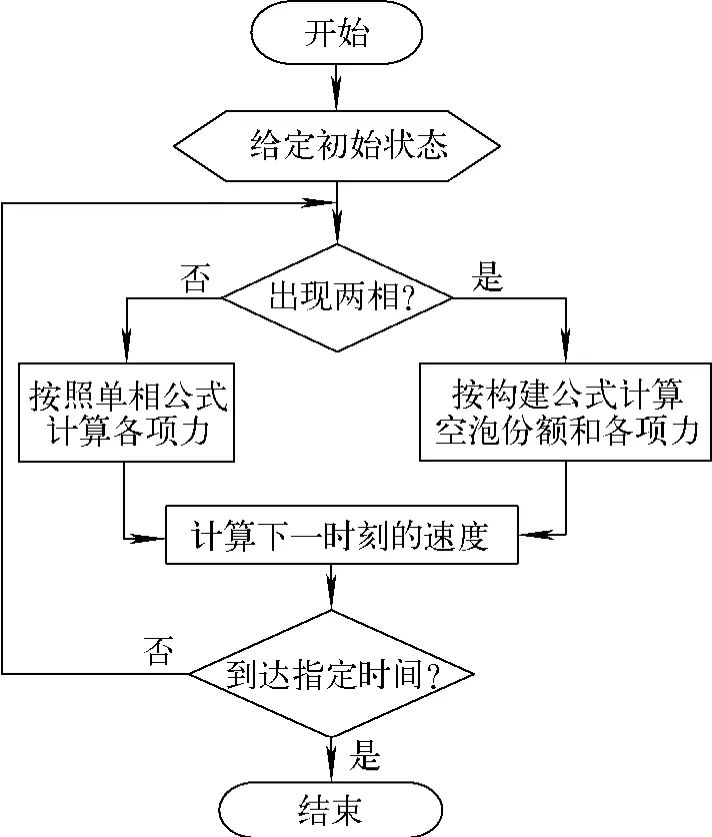
图2 主程序框图Fig.2 Main flow chart
1.2 计算结果与实验结果对比
波谷型脉动起始点对应功率及流量的实验值和计算值的对比如图3所示,可看出,实验和计算的波谷型脉动起始点功率误差大部分都在20%以内,由于瞬态计算的复杂性,计算精度较为理想,其规律性能够得以体现。流量的计算值和实验值基本吻合,验证了模型的正确性。
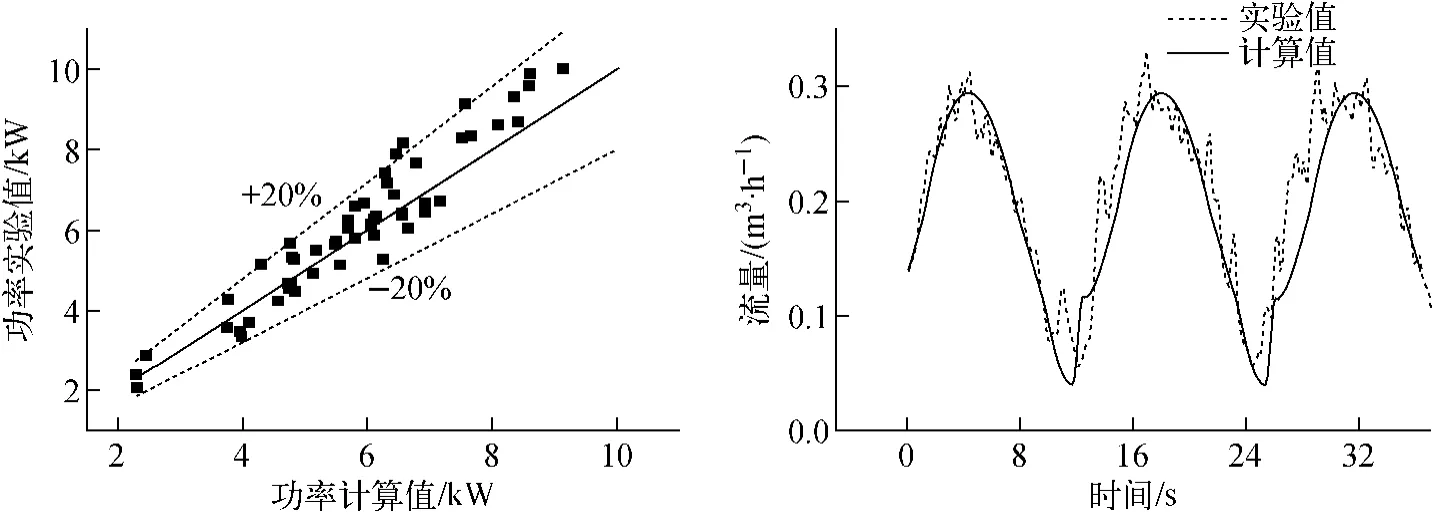
图3 功率和流量的实验值和计算值比较Fig.3 Comparison of calculated and experimental results for power and flow rate
2 摇摆振幅对波谷型脉动的影响
2.1 摇摆振幅对波谷型脉动起始点对应功率的影响
图4为摇摆振幅改变时波谷型脉动起始点对应功率的变化。随着摇摆振幅的增加,脉动起始点对应功率下降。由于摇摆振幅越大,系统的摩擦阻力系数越大,平均流量越小;且摇摆振幅越大,摇摆附加力越大,流量波动幅度也越大,系统波谷处流量越低,因此脉动起始点对应功率越小。
2.2 摇摆振幅对波谷型脉动流量的影响
不同摇摆振幅下,波谷型脉动发生时系统流量也发生变化。图5为不同摇摆振幅(A)下波谷型脉动发生时的流量。图6为同一工况下1个周期内的出口壁温和水温。
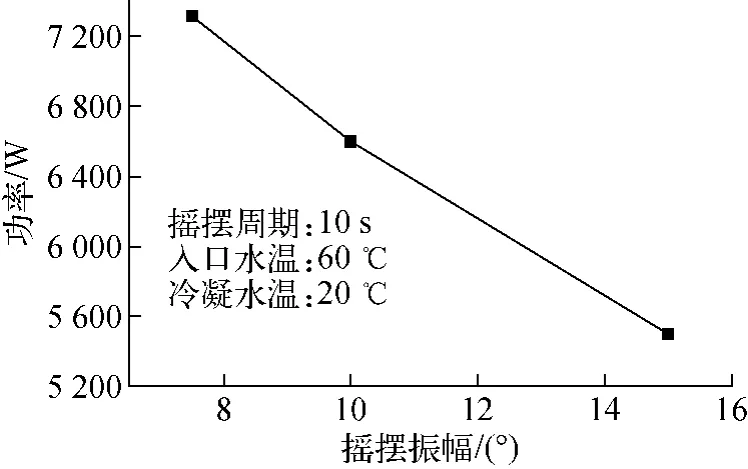
图4 改变摇摆振幅时波谷型脉动起始点对应的功率Fig.4 Power of pulse starting point corresponding to different rolling amplitudes
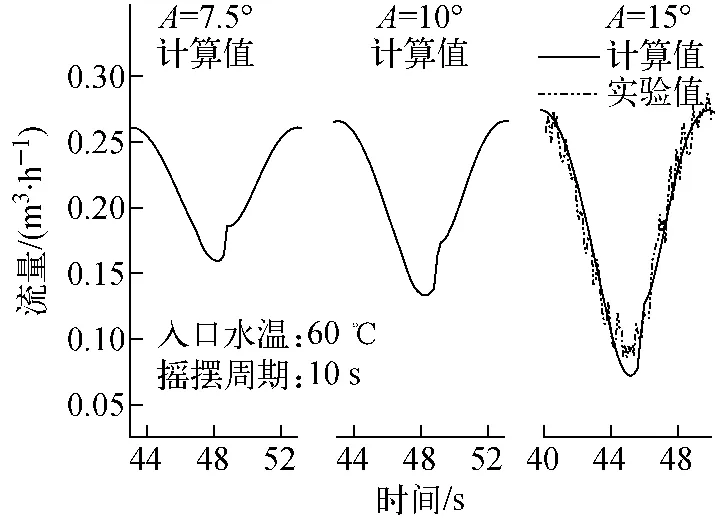
图5 改变摇摆振幅时流量的比较Fig.5 Comparison of flow rates in different rolling amplitudes
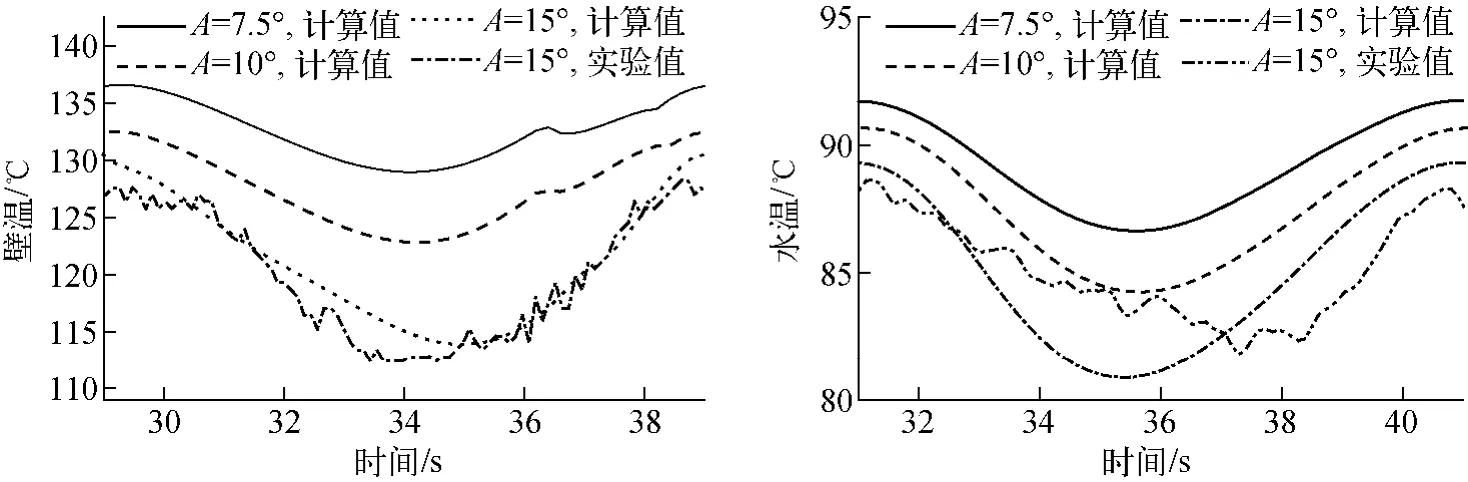
图6 不同摇摆振幅下壁温及加热段出口水温的比较Fig.6 Comparison of wall and outlet water temperatures in different rolling amplitudes
从图5可看出,随着摇摆振幅的增加,流量波动幅度增加,流量在波谷附近上升段的斜率较下降段斜率大。波谷处流量的变化较波峰处流量的变化大,这是因为在相同功率时,随着摇摆振幅的增加,阻力系数增加,平均流量降低,波谷处流量的变化较波峰处流量的变化大。而对于波谷型脉动,摇摆振幅变大时脉动起始点对应功率降低,阻力增加和功率降低两者相结合,使得摇摆振幅变大时波谷处流量变化大。
2.3 摇摆振幅对波谷型脉动壁温的影响
从图6a可看出,摇摆振幅越大,发生波谷型脉动后对应壁温的平均值越低,这是因为对于波谷型脉动,摇摆振幅越大,对应功率越低。且摇摆振幅越大,流量波动越大,壁温波动幅度也越大。从图中还可看出,在壁温上升阶段,其温度有一个略微下降而后上升的阶段。这是因为该处开始产汽,换热系数增加,流体带走的热量增加,导致壁温下降,但经过这个短暂的下降阶段之后会接着上升。由于流体的平均温度是上升的,壁温不会一直随换热系数的增加而降低,在产汽后其整体趋势还是上升的。
2.4 摇摆振幅对波谷型脉动出口水温的影响
对于波谷型脉动,摇摆振幅改变后,流量发生变化,加热段出口水温也发生变化。当功率相同时,摇摆振幅越大,平均流量越低,加热段的出口水温平均值越高。但对波谷型脉动而言,摇摆振幅增加时脉动起始点对应功率降低,功率降低和流量降低两者共同影响加热段出口水温的平均值,其结果是摇摆振幅越大,出口水温平均值越小,波动幅度越大。
图6b中,加热段出口水温测量值和计算值具有一定差别,水温波动幅度较小,相位滞后。由于水温具有记忆效应,加热需要一定时间,而计算过程对这一现象考虑不够充分,导致实际水温波动大,相位提前,因此水温的计算值和实验值出现了如图所示的差别。由于壁温能很快响应流量的变化,所以壁温的计算值和实验值符合程度较好。
3 摇摆周期对波谷型脉动的影响
3.1 摇摆周期对波谷型脉动起始点对应功率的影响
随摇摆周期的增加,波谷型脉动起始点对应功率增加(图7)。这是因为随摇摆周期的增加,流量的波动幅度变弱,最低流量和平均流量升高,产汽点对应的功率和脉动起始点功率增加,与摇摆振幅减小时的结果一致。

图7 改变摇摆周期时波谷型脉动起始点对应的功率Fig.7 Power of pulse starting point corresponding to different rolling periods
3.2 摇摆周期对波谷型脉动流量的影响
图8为不同摇摆周期(T)下波谷型脉动发生时的流量、出口水温和壁温。从图8a可看出,不同摇摆周期下发生波谷型脉动时,摇摆周期越小,流量波动幅度越大,且波谷处流量的变化较波峰处的大。减小摇摆周期时流量的变化趋势与增大振幅时的趋势一致。增大振幅与减小摇摆周期都是加剧摇摆程度,因此影响一致。
3.3 摇摆周期对波谷型脉动出口水温的影响
从图8b可见,摇摆周期越小,摇摆程度越剧烈,出口水温平均值越小,与增大摇摆振幅的结果一致。但水温波动幅度并不随摇摆剧烈程度的增大而增大。摇摆周期小时,水温波动幅度较小,随摇摆周期的增加,水温波动幅度先增加后减小。这是因为摇摆周期小时,虽然摇摆程度剧烈,但水温具有“记忆”效应,其温升是积累量,上升需要一定时间,摇摆周期小时水温来不及变化,所以摇摆周期越小水温波动幅度越小。随摇摆周期的增加,水温响应时间增加,因而摇摆周期越长,水温波动幅度越大。
3.4 摇摆周期对波谷型脉动壁温的影响
图8c为不同摇摆周期下发生波谷型脉动后壁温的变化。摇摆周期越小,壁温平均值越小,壁温波动幅度越大。改变摇摆周期时壁温波动幅度和水温波动幅度不对应,因为壁温变化是局部效应,能及时响应流量的变化。但流体处于流动加热过程,当流量变化时,出口水温不能立刻随之变化,需要一定时间来响应。当摇摆周期小时,响应时间不够,出口水温波动幅度较小,壁温在实验周期范围内能及时响应,且流量波动越大,壁温变化越剧烈。
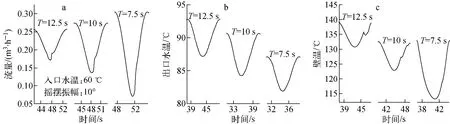
图8 不同摇摆周期下发生波谷型脉动时的流量、出口水温和壁温Fig.8 Flow rate,outlet water and wall temperatures in different rolling periods
4 摇摆对波谷型脉动的影响机理分析
影响流动变化的主要因素是驱动力、摇摆运动引起的附加力和阻力,因此从它们的变化来阐述摇摆参数对波谷型脉动的影响。摇摆条件下,摇摆振幅的增加和摇摆周期的减小有相似的效果,因此只对改变摇摆振幅后的各项压降进行分析。图9示出了不同摇摆振幅下重位压降(驱动压头)、摇摆附加压降、局部摩擦压降和流量随时间的变化。
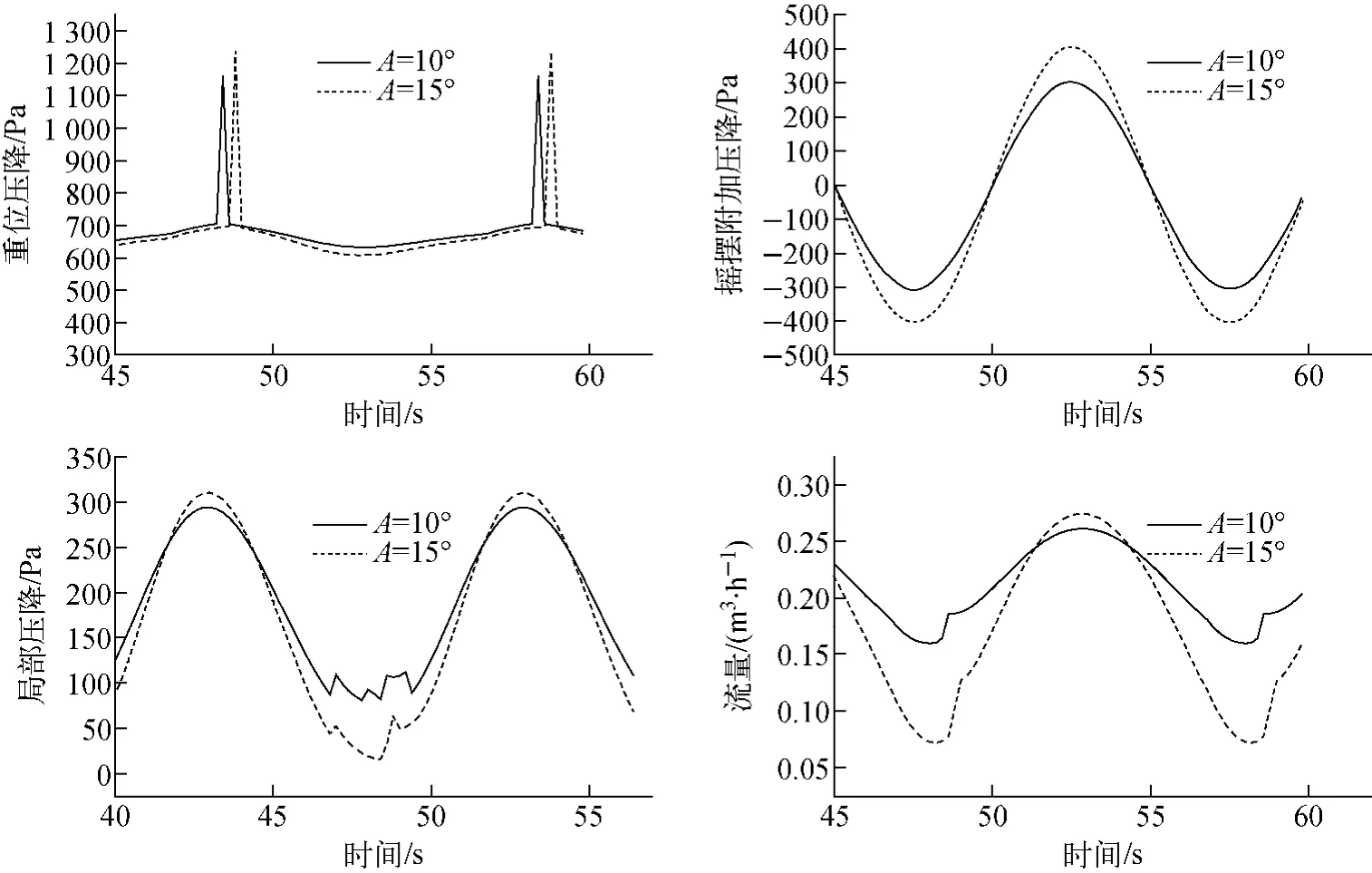
图9 不同摇摆振幅下的重位压降、摇摆附加压降、局部摩擦压降和流量Fig.9 Gravity pressure drop,additional pressure drop caused by rolling,local friction pressure drop and flow rate in different rolling amplitudes
产汽在低流量下发生,所产汽体需要一段时间才能到达上升段并提供驱动力,驱动压头的变化较含汽率有一个滞后,因而在产汽后,阻力增加大于驱动力增加,引起流量先降低;当重位压降增幅较大时,才会带动流量有一大的提升,并导致流量脉动曲线总体呈上升快下降慢的非对称形式。在波谷附近,重位压降变化剧烈,和局部摩擦压降交替影响波谷处的流量。
驱动力包括重位压降和摇摆引起的附加压降两项。重位压降的升高在波谷处的流量上升阶段起主导作用,但仅在波谷后很短一段时间起作用。而整体过程中,从附加压降和重位压降的对比可看出,不同摇摆振幅下,重位压降的变化较附加压降的变化小很多。因此,整个周期内对流量变化起主要作用的仍是摇摆引起的附加压降。
综上所述,摇摆运动下,在波谷型脉动整体过程中起主要作用的是摇摆运动引起的附加压降,但在波谷附近,局部摩擦压降和重位压降变化较大,交替影响流动,诱发了波谷型脉动。
5 结论
本文构建了摇摆条件下自然循环波谷型脉动的计算分析模型,计算结果和实验结果符合较好,通过模型对波谷型脉动进行了分析和研究,得到如下结论:
1)对于摇摆运动下的波谷型脉动,其整体流动波动过程中起主导作用的是摇摆运动引起的附加压降,而在波谷附近由于产汽的影响,局部摩擦压降和重位压降交替主导流动,并最终诱发波谷处的流动不稳定性。
2)摇摆振幅和频率越大,即摇摆程度越剧烈,摇摆引起的附加力变化越大,流量、壁温等热工参数波动幅度越大。水温波动幅度变化受摇摆程度和水温记忆效应两方面的影响,因而随摇摆周期的增加呈现先增加后减少的非线性变化。
3)摇摆程度越剧烈,平均流量和最低流量越低,进而导致波谷型脉动起始点对应功率降低。
本研究构建的计算波谷型脉动的模型,尚有很多考虑不周之处,还有待于进一步的机理性实验研究来加以改进和完善。
[1] TAN S C,SU G H,GAO P Z.Experimental study on two-phase flow instability of natural circulation under rolling motion condition[J].Annals of Nuclear Energy,2009,36(1):103-113.
[2] MURATA H,SAWADA K,KOBAYASHI M.Natural circulation characteristics of a marine reactor in rolling motion and heat transfer in the core[J].Nuclear Engineering and Design,2002,215(1-2):69-85.
[3] 杨珏,贾宝山,俞冀阳.海洋条件下冷却剂系统自然循环仿真模型[J].核科学与工程,2002,22(2):125-129.
YANG Jue,JIA Baoshan,YU Jiyang.Simulation model of natural circulation in PWR coolant system under ocean conditions[J].Chinese Journal of Nuclear Science and Engineering,2002,22(2):125-129(in Chinese).
[4] 杨珏,贾宝山,俞冀阳.简谐海洋条件下堆芯冷却剂系统自然循环能力分析[J].核科学与工程,2002,22(3):199-203.
YANG Jue,JIA Baoshan,YU Jiyang.Analysis of natural circulation ability in PWR coolant system under ocean condition[J].Chinese Journal of Nuclear Science and Engineering,2002,22(3):199-203(in Chinese).
[5] ISHIDA T,KUSUNOKIB T,MURATA H.Thermal-hydraulic behavior of a marine reactor during oscillations[J].Nuclear Engineering and Design,1990,120(2-3):213-225.
[6] 谭思超,张红岩,庞凤阁,等.摇摆运动下单相自然循环流动特点[J].核动力工程,2005,26(6):554-558.
TAN Sichao,ZHANG Hongyan,PANG Fengge,et al.Characteristics of single-phase natural circulation under rolling[J].Nuclear Power Engineering,2005,26(6):554-558(in Chinese).
[7] 郭赟,秋穗正,苏光辉,等.摇摆状态下入口段和上升段对两相流动不稳定性的影响[J].核动力工程,2007,28(6):58-61.
GUO Yun,QIU Suizheng,SU Guanghui,et al.Effect of inlet and riser sections on two-phase flow instability under rolling[J].Nuclear Power Engineering,2007,28(6):58-61(in Chinese).
[8] 谭思超,高璞珍.摇摆运动条件下自然循环复合型脉动的实验研究[J].原子能科学技术,2008,42(11):1 007-1 011.
TAN Sichao,GAO Puzhen.Experimental research on natural circulation complex oscillations under rolling motion conditions[J].Atomic Energy Science and Technology,2008,42(11):1 007-1 011(in Chinese).
[9] PRASAD R O S,DOSHI J B.A numerical investigation of nuclear coupled density wave oscillations[J].Nuclear Engineering and Design,1995,154(3):381-396.
[10]TAN S C,SU G H.Experimental and theoretical study on single-phase natural circulation flow and heat transfer under rolling motion condition[J].Nuclear Engineering and Design,2009,239(10):2 212-2 216.
Influence of Rolling Parameter on Trough Fluctuation in Natural Circulation
ZHANG Xiao-yu1,TAN Si-chao1,*,YU Zhi-ting1,SONG Yu-lin1,ZHANG Hong2
(1.Fundamental Science on Nuclear Safety and Simulation Technology Laboratory,
Harbin Engineering University,Harbin150001,China;2.Science and Technology on Reactor System Design Technology Laboratory,Nuclear Power Institute of China,Chengdu610041,China)
The influence of rolling parameters on trough fluctuation in natural circulation was researched.The mathematical model was developed to simulate trough fluctuation and the calculated results fit well with the experimental results.The calculated results indicate that for trough fluctuation under rolling motion,the additional force caused by rolling motion plays a main role in the whole flow fluctuation process,while near the trough,the local friction pressure drop and driving force caused by gravity dominate the flow alternately,which eventually induces instability near the trough.The bigger the amplitude and frequency of rolling motion are,namely the more intense the rolling motion is,the bigger the fluctuation of driving force caused by rolling is,thus causing larger fluctuation of flow rate and wall temperature,thereby the power corresponding tothe starting point of trough instability is lower.
rolling motion;natural circulation;trough fluctuation;flow instability
TL333
:A
:1000-6931(2015)01-0040-07
10.7538/yzk.2015.49.01.0040
2013-11-13;
2014-05-08
教育部留学归国基金资助项目(2012-1707);黑龙江省青年学术骨干支持计划资助项目(1254G017);核反应堆系统设计技术重点实验室基金资助项目(KZAK-A-1101)
张晓玉(1989—),女,河南安阳人,硕士研究生,核能科学与工程专业
*通信作者:谭思超,E-mail:tansichao@hrbeu.edu.cn

