γ探测死时间与计数修正因子的关系
伍怀龙,章剑华,储诚胜,胡广春,张昌繁,胡 根,龚 建,田东风
(中国工程物理研究院核物理与化学研究所,四川绵阳 621900)
γ探测死时间与计数修正因子的关系
伍怀龙,章剑华,储诚胜,胡广春,张昌繁,胡 根,龚 建,田东风
(中国工程物理研究院核物理与化学研究所,四川绵阳 621900)
为在γ放射性活度很大的测量中使测量系统得到更好的准确度,本文使用干扰源研究HPGe探测器得到了测量系统死时间与计数损失的关系。在γ能量为0.3~1.3MeV时进行实验,使用104~105Bq量级的放射源,修正能峰的计数率一般保持在几十s-1,证明在误差范围(3%)内,计数损失随死时间变化的关系与射线能量和计数强度无关,任意强度的任意核素均可使用这一修正公式进行计数损失修正。
γ测量;计数损失;死时间
所有射线(包括γ射线)的测量均存在死时间。这是由于探测器的电子学线路处理每个进入的粒子或光子时均需花一时间(响应时间)。当进入探测器的射线强度太大时,存在前一个射线还未处理完而下一个射线已进入的情况。那么第2个射线就有可能不能被处理,此即死时间效应。
高纯锗探测器系统的死时间是影响测量准确度的一个因素。一般,死时间较大会造成测量得到的计数发生损失,即测得的计数较实际的偏小。对于一正常的探测器,测量系统死时间较大的唯一原因是测量的计数率过大,故测量强源(约定活度在106Bq以上的为强源,活度在105Bq以下的为非强源)时会由于测量系统死时间增大而使测量结果不准确。因此,测量强源时需对由于死时间增大带来的误差进行评价[1],并找到一合适的方法对这一误差进行修正。一般在用的探测器若可进行强放射性测量,则需对测量结果进行死时间修正。文献[2]用一台高纯锗γ射线探测器谱仪对一已知活度的137Cs源(单能661.67keV)的测量结果进行了修正。本文将更深入地研究死时间问题,通过不同的高纯锗γ探测器谱仪的修正实验,研究证明修正公式对各能量的γ射线基本一致,以及修正公式基本不随计数强度的变化而变化。
1 实验方案
死时间造成计数损失[3]的影响包括两方面:1)待测核素本身活度较强;2)干扰源(即非目标测量核素)活度较强。由于没有活度已知的强放射源,实验采用一个干扰源,放在与探测器相距不同的位置,使探测器系统死时间发生变化,来观测待测核素计数率的变化。实验需保持待测源位置不动,所以它的计数变化完全是由于测量系统死时间的变化引起的。
使用一强待测源放在距探测器不同的位置进行实验。此时,需确定待测源位置变动时各位置的探测效率,这尽管可在较大精度下确定探测效率[4],但也引入了一不确定因素。为在进行修正实验时尽量无其他因素干扰,采取的另一方案是保持待测源几何位置完全不动,用另一干扰源使测量系统死时间变化,以确定死时间变化时待测源测量所需的修正方法。
首先,认为与计数损失有关的变量可能是测量系统死时间、γ射线能量和光电峰强度,则计数修正因子CR有:

式中:Iγ为光电峰真实强度;Ic为光电峰测量强度;E为γ射线光电峰能量;DT为死时间分数。
为证明死时间修正公式仅与死时间的数值有关,即用实验室的标准源得到的通过干扰源使死时间增大而作出的死时间修正公式可用于以后对任意核素的测量,需证明计数修正因子CR(E,Ic,DT)与γ射线光电峰能量E、光电峰测量强度Ic无关,而只与测量系统死时间分数DT有关。即要证明有如下关系存在:
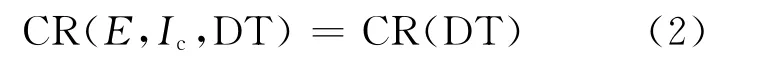
若式(2)被证明是正确的,那么使用实验室强度较小的标准源所作的在某能量处(如137Cs的661.67keV)的死时间修正公式,就可直接用于将来测量其他能量强峰的修正。
由此,实验安排如下:使用152Eu作为干扰源,放在探测器侧面不同距离处,以使系统死时间发生变化;使用133Ba、60Co、137Cs作为测量源放于探测器正面的固定位置,对这3种核素的276.04、302.85、356.02、383.85、661.67、1 173.23、1 332.49keV 7个能量的γ射线峰进行计数损失修正分析。对每个能量峰均可作出计数随死时间的修正曲线。若能确定这些修正曲线在误差范围(3%)内是一致的,则可证明计数修正因子CR(E,Ic,DT)与光电峰能量E无关。
然后,将133Ba、60Co、137Cs源放于探测器正面的不同位置,使这7个能量峰的计数强度发生变化,作出计数随死时间的修正曲线。若能确定这些曲线在误差范围内是一致的,则可证明计数修正因子CR(E,Ic,DT)与光电峰计数强度Ic无关。
2 实验与结果
本实验所使用的标准源为152Eu(7.098× 105Bq)、133Ba(2.247×105Bq)、137Cs(2.404× 105Bq)、60Co(1.979×105Bq)。各核素所使用的参数见文献[5]。γ能谱解谱使用自主编写的γ能峰解谱软件[6]。
采取的实验步骤如下。
1)将测量源60Co、137Cs放于探测器正面15cm处,干扰源152Eu放于侧面不同位置以使死时间发生变化,得到的结果示于图1、2。
2)将测量源133Ba放于探测器正面15cm处,干扰源152Eu放于侧面不同位置以使死时间发生变化,得到的实验结果示于图1。
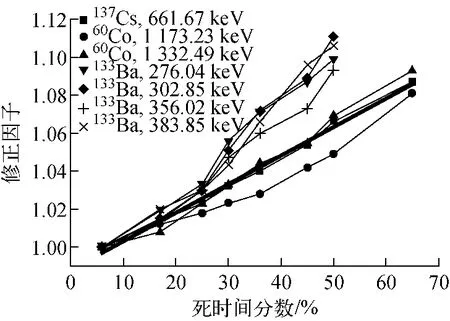
图1 测量源60Co、137Cs和133Ba放置于15cm处的修正结果和拟合曲线Fig.1 Correct results and simulation curves with distance of 15cm for60Co,137Cs and133Ba

图2 测量源60Co、137Cs放置不同位置处修正结果和拟合曲线Fig.2 Correct results and simulation curves at various positions of60Co and137Cs
3)将测量源60Co、137Cs放于探测器正面10cm处,干扰源152Eu放于侧面不同位置以使死时间发生变化,得到的结果示于图2。
4)将测量源60Co、137Cs放于探测器正面5cm处,干扰源152Eu放于侧面不同位置以使死时间发生变化,得到的结果示于图2。
步骤1和2检验计数损失修正公式在不同能量处是否一致。步骤3和4检验在测量γ射线峰强度变化时对它们的计数损失修正公式是否一致。
根据图1示出的60Co、137Cs和133Ba的7个能量的修正曲线,使用拟合公式:
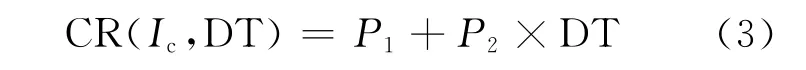
从图1可看出,对不同能量γ射线峰,计数的修正因子随死时间的变化是一致的,所以式(3)中的计数修正因子CR(Ic,DT)与能量无关。
根据式(3)拟合出图1中计数修正曲线(粗线),这时拟合系数P1为0.988 02,系数P2为0.001 5。
根据图2示出的60Co、137Cs源在不同位置时的计数修正曲线,使用与式(3)类似的拟合公式:
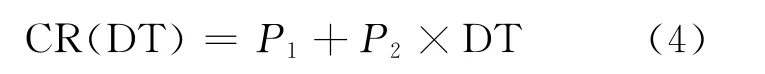
从图2可看出,不同位置测量的峰计数强度不同,但计数修正因子随死时间的变化一致,绝大多数数据点与拟合线的差异在3%以内,所以式(4)中的计数修正因子CR(DT)与γ射线光电峰测量强度Ic无关。
根据式(4)拟合出图2的计数修正曲线(图2中粗线),这时P1为0.988 02,P2为0.001 5。
需说明的是,式(3)、(4)的拟合均是使用图1、2中不同位置、不同能量在相同死时间下计数损失的平均值进行的。
3 数据分析
对图1、2进行误差分析,得到净计数率n0与总计数率ns和康普顿平台本底计数率nb的关系[9]为:
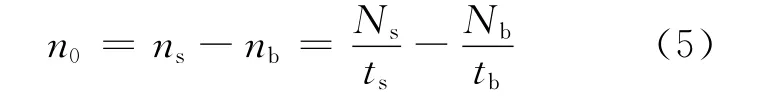
根据误差传递公式得到标准误差:
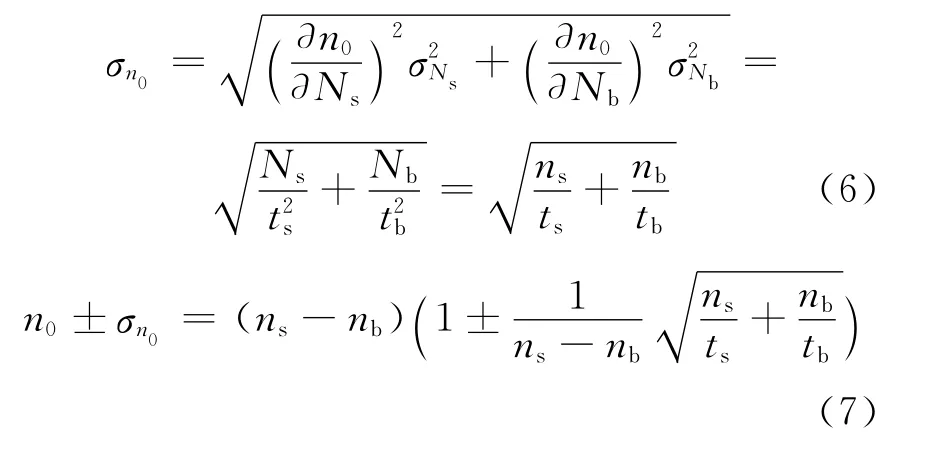
4 小结
本文使用干扰源研究得到了测量系统死时间与计数损失的关系。研究发现,计数修正因子CR(E,Ic,DT)与γ射线光电峰能量、光电峰测量强度无关,仅与测量系统死时间分数有关。在以后进行的任意强放射性核素测量时均可使用相同的修正公式,且这种修正方法主要针对的是HPGe探测器。
[1] 伍怀龙,田东风.武器级钚材料丰度和年龄测量研究[J].中国科学E,2009,39(2):261-265.WU Huailong,TIAN Dongfeng.Investigation of weaponry plutonium abundance and age analysis[J].Science in China E,2009,39(2):261-265(in Chinese).
[2] 伍怀龙,杨晓波,唐元明.死时间和源不均匀性对γ测量准确性的影响,中国核科技报告CNIC-01760CAEP-0142[R].绵阳:中国工程物理研究院,2005.
[3] 陈伟,冯天成,晏林,等.几套就地HPGeγ谱仪系统的死时间修正[J].原子能科学技术,2010,44(5):589-594.
CHEN Wei,FENG Tiancheng,YAN Lin,et al.Deadtime correction of several in-situ HPGeγ spectrometers[J].Atomic Energy Science and Technology,2010,44(5):589-594(in Chinese).
[4] LABSOCS manual[M].USA:CANBERRA Inc.,2005.
[5] RICHARD B.Firestone 1996table of isotope[M].8th ed.USA:Lawrence Berkeley National Laboratory,1996.
[6] 伍怀龙,刘素萍,龚有进,等.辐射指纹的解析技术研究[J].原子能科学技术,2006,40(1):10-14.
WU Huailong,LIU Suping,GONG Youjin,et al.Investigation of gamma spectra analysis[J].Atomic Energy Science and Technology,2006,40(1):10-14(in Chinese).
Relationship betweenγDetection Dead-time and Count Correction Factor
WU Huai-long,ZHANG Jian-hua,CHU Cheng-sheng,HU Guang-chun,ZHANG Chang-fan,HU Gen,GONG Jian,TIAN Dong-feng
(Institute of Nuclear Physics and Chemistry,China Academy of Engineering Physics,Mianyang621900,China)
The relationship between dead-time and count correction factor was investigated by using interference source for purpose of highγactivity measurement.The count rates maintain serval 10s-1withγenergy of 0.3-1.3MeV for 104-105Bq radioactive source.It is proved that the relationship between count loss and dead-time is unconcerned at various energy and various count intensities.The same correction formula can be used for any nuclide measurement.
γdetection;count loss;dead-time
O571.4
:A
:1000-6931(2015)01-0162-04
10.7538/yzk.2015.49.01.0162
2013-07-11;
2014-04-22
国家自然科学基金资助项目(11375157)
伍怀龙(1972—),男,重庆人,副研究员,博士,从事核物理测试与核技术应用研究

