多线铁路拱加劲连续梁桥上无缝线路梁格模型＊

于向东，吴志花，闫 斌

（中南大学 土木工程学院，湖南 长沙 410075）

拱加劲连续梁桥具有跨越能力大、结构刚度强、造型美观等优点，且有效降低了上部结构对墩和基础刚度的要求［1－3］，在我国高速铁路建设中的应用日益广泛．拱加劲连续梁桥空间性比较强，桥上常铺设多线轨道，其桥梁和轨道结构的受力情况较为复杂．

目前对拱加劲连续梁桥上无缝线路纵向力的相关研究相对较少，且研究所用模型多为平面模型［4－11］．平面模型无法考虑梁体的横向变形和活载的空间分布特性，仅适用于宽跨比不大的单线窄箱梁桥，采用平面模型研究多线拱加劲连续梁桥上无缝线路受力规律，其适用性仍有待商榷．

与平面模型相比，梁格模型更能体现多线拱加劲连续梁桥的结构及荷载布置的空间性，相对于实体模型也更加简便快捷．

本文基于梁格法，采用通用有限元分析软件建立某（36＋112＋36）m 拱加劲连续梁桥的空间梁格模型，与传统的平面杆系模型计算结果进行对比．探讨拱加劲连续梁桥结构及荷载的空间特性对桥上轨道结构纵向力分布规律的影响．

1 梁轨计算模型及计算参数

1．1 工程背景

本工程为成都至兰州线某（36＋112＋36）m 双线拱加劲连续梁桥．主梁为“Π”形截面预应力混凝土箱梁，纵梁间桥面结构采用纵、横梁体系格子梁．桥上铺设双线有砟轨道，线间距4．48 m，采用Ⅲ型混凝土轨枕、弹条Ⅴ型小阻力扣件．

1．2 平面模型

建立考虑梁轨相互作用的平面杆系模型，主梁由带竖向刚臂的梁单元模拟，梁轨之间的纵向连接由非线性弹簧模拟，拱肋、腹杆以及钢轨均由梁单元模拟，吊杆由仅受拉桁架单元模拟，路基上的钢轨长度取为200m［12］，固定支座处桥墩的水平位移由等效刚度弹簧模拟，墩顶纵向线刚度取为1 000kN／cm［13］．平面有限元模型及桥跨布置如图1所示．线路纵向阻力采用理想弹塑性模型［13］．

道床纵向阻力：

小阻力扣件纵向阻力：

式中：r为线路纵向阻力，（kN／m）／轨；u为梁轨纵向相对位移，mm．

图1 平面有限元模型及桥跨布置（单位：m）Fig．1 Plane finite element model and arrangement of bridge spans（unit：m）

1．3 梁格模型

梁格模型是将复杂结构的纵、横向刚度等效分散于相应的各纵、横向梁格构件中，从而形成一个空间梁格体系，当梁格体系承受与原型实体结构相同荷载时，两者的受力、变形近似接近［14－15］．为保证与实际结构变形相符，纵梁划分时应尽量保证各纵向梁格构件中性轴与实际结构一致．本桥的主梁结构较为复杂，不能通过一次划分满足中性轴一致原则，故要强制移轴．由于实际结构横梁布置比较密集，纵向可不增设虚拟横梁；为避免过多的弹性连接造成计算结果奇异，横向需增设零容重虚拟横梁以满足纵横梁之间的共节点连接．梁轨之间非线性约束以及其他构件的模拟均与平面模型相同．本文所建立的梁格模型如图2所示．

1．4 计算参数

计算钢轨伸缩力时，有砟轨道混凝土梁日温差考虑整体升温15℃，拱肋及风撑日温差考虑整体升温15 ℃［13］，不考虑温度梯度．

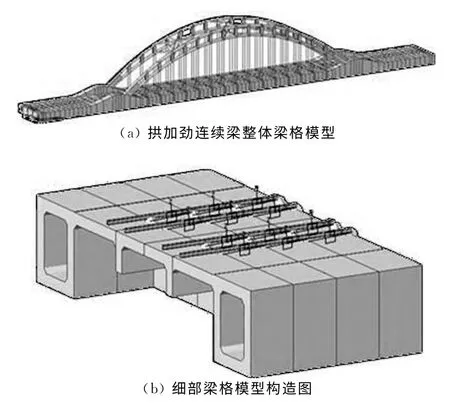
图2 梁格模型Fig．2 Grillage model

计算钢轨挠曲力时，上翼缘纵向位移不考虑冲击系数，并将列车活载换算成均布荷载［13］，列车活载取用中－活载．连续梁计算挠曲力时简化为在固定支座至梁端的多跨梁上布载［13］．将活载简化为左边跨布载、左边跨与中跨同时布载、满跨布载、中跨布载、中跨与右边跨同时布载和右边跨布载6种不利方式加载，计算时取6种工况下的包络值．

计算钢轨制动力时，轮轨黏着系数取为0．164［13］，加载方式同挠曲力．考虑到支座布置方式不对称且轨道为双线，制动力加载方式分为对向制动、单线制动和单线反向制动3种情况．

计算钢轨断轨力时，考虑钢轨在拱加劲连续梁桥的钢轨受力峰值位置折断，受力峰值分别出现在两侧梁端处．最高轨温57．1 ℃，最低轨温－5．9 ℃，钢轨最大降温45 ℃［13］．

2 计算模型的验证

文献［11］建立了32m 简支梁桥的平面模型和实体模型研究桥上无缝线路的受力特性．本文建立了计算结果与其一致的32 m 简支梁桥的平面模型，并建立同一工程背景的梁格模型，将计算结果与文献［11］对比，见表1．

表1 不同有限元模型计算结果比较Tab．1 Results comparison of different finite element models

本文所建平面模型与文献［11］的计算结果接近，两者比值为1．00～1．02，证明本文采用的32m简支梁桥轨道相互作用分析方法的正确性．本文所建立的梁格模型与实体模型的计算结果较为接近，两者比值为1．02～1．06，证明本文所建的梁格模型可代替实体模型研究多线桥梁上的梁轨相互作用问题．

3 桥上无缝线路模型对比

3．1 钢轨伸缩力

分别计算梁格模型及平面模型中拱加劲混凝土连续梁桥整体升温15 ℃工况下钢轨伸缩应力和钢轨位移，如图3所示．

2种模型计算得到的钢轨伸缩应力和位移基本一致．最大伸缩拉应力出现在拱加劲连续梁桥跨中附近，最大伸缩压应力出现在远离固定支座的梁端．钢轨在两侧梁端处均有突变，原因是主梁在此处设置了断开，使得温度作用下钢轨的伸缩拉应力得到一定程度的释放．梁格模型下，钢轨最大伸缩拉应力为30．2MPa，最大伸缩压应力为48．8MPa；平面模型为31．2 MPa和53．9 MPa．

由于路基的约束限制了钢轨位移，钢轨在拱加劲连续梁桥固定支座旁的边跨上出现向左移动位移最大值，在跨中活动支座处出现向右移动位移最大值．梁格模型下，钢轨最大位移为9．2 mm；平面模型为11．1mm．温度作用下，梁格法与传统的平面模型计算所得的钢轨伸缩力差别不大．

梁体升温15℃，梁格模型和平面模型计算所得的墩顶水平力分别为385．6kN 和289．7kN．

3．2 钢轨挠曲力

取对向加载时梁格模型和平面模型6种工况下的挠曲应力包络值进行比较，如图4所示．

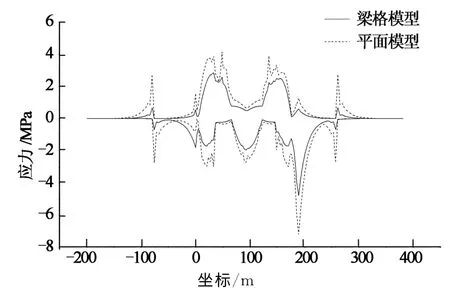
图4 钢轨挠曲应力包络图对比Fig．4 Comparative results of the envelope diagram in bending rail stress

2种模型中由中－活载引起的钢轨挠曲应力变化规律比较一致．路基与主梁连接处的断开造成的应力释放，使得梁端挠曲应力突变，但远离固定支座处突变明显，靠近固定支座处突变偏小．平面模型的计算值偏保守．钢轨挠曲压应力在远离固定支座的梁端达到最大值，梁格模型为4．8MPa，平面模型为7．2 MPa．钢轨挠曲拉应力在桥梁跨中两支座处均达到峰值，梁格模型跨中固定支座处为2．9MPa，跨中活动支座处为2．5 MPa；平面模型为3．9 MPa和3．4 MPa．

中－活载下，梁格模型和平面模型计算所得的最大墩顶水平力分别为47．7kN 和51．1kN．

3．3 钢轨制动力

钢轨制动力加载方式同挠曲力，共6种工况．取梁格模型和平面模型对向制动6种工况下的包络值进行比较，如图5（a）所示，取梁格模型有载线及无载线和平面模型在单线制动和单线反向制动6种工况下的包络值进行比较，如图5（b）和（c）所示．

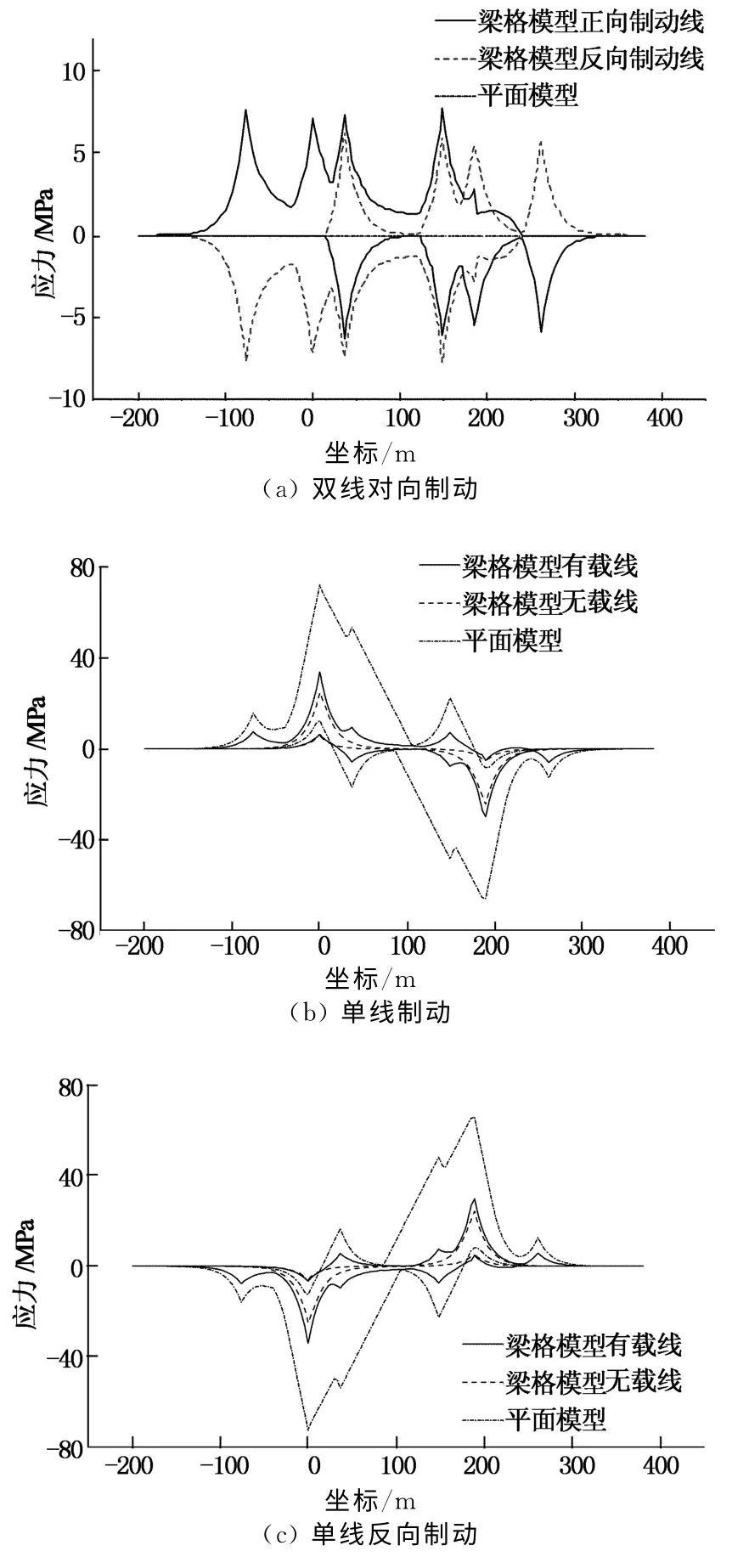
图5 钢轨制动应力包络图对比Fig．5 Comparative results of the envelope diagram in rail braking stress

平面模型无法模拟对向制动工况，双线对向制动作用下，应力值均为零．梁格模型由中－活载引起的钢轨制动应力在线上出现多处峰值．梁格模型下正向制动线最大拉应力值为7．8 MPa，最大压应力值为6．3 MPa，反向 制 动线 为6．3 MPa 和7．8 MPa．正向制动应力和反向制动应力数值接近、符号相反．靠近固定支座处最大钢轨制动应力是远离固定支座处的1．1倍．支座布置方式不对称对钢轨制动应力有影响．

单线制动作用下，由于拱加劲连续梁桥有很强的整体性，有载线和无载线变化规律较一致，数值也较接近，有载线最大拉、压应力为34．0MPa和29．8 MPa，无载线为25．0 MPa和24．4 MPa．而拱加劲连续梁桥又有很强的空间性，故有载线的应力包络图存在多处峰值，而无载线只在梁端处达到峰值，然后迅速向两侧衰减．

平面模型的应力包络图与梁格模型有载线变化规律一致，但其数值远大于梁格模型有载线、无载线．平面模型在梁端和路基上的拉应力峰值各为72．6 MPa，15．9 MPa；梁格模型有载线对应峰值各为34．0 MPa，7．7 MPa，无载线在梁端为25．0 MPa，路基上则为零．平面模型无法准确反映桥上多线无缝线路的受力情况．

单线制动与单线反向制动2种情况下的应力包络图均关于跨中对称．

中－活载下，计算梁格模型和平面模型在单线制动、单线反向制动和对向制动3种工况下的最大墩顶水平力，结果见表2．

表2 不同模型下最大墩顶水平力Tab．2 The maximum horizontal force of different models on pier kN

对向制动时，平面模型无法正确反映墩顶水平力，梁格模型正向制动线和反向制动线墩顶水平力数值相等、方向相反．平面模型与梁格模型计算所得的最大墩顶水平力相差很大．

3．4 钢轨断轨力

钢轨降温45℃，计算梁格模型和平面模型中钢轨在拱加劲连续梁两侧梁端处分别折断引起的钢轨断轨应力和钢轨位移，仅考虑钢轨降温45℃引起的断轨应力和位移，计算结果如图6所示．

图6 钢轨断轨工况计算结果对比Fig．6 Comparative results in rail breaking situation

梁格模型和传统的平面模型计算所得的钢轨断轨应力较为接近．在断轨处钢轨应力均为0，并向两侧迅速增大；在梁端，主梁断开使得断轨应力得到一定程度的释放，故在梁端处断轨应力均有突变．平面模型计算得到的钢轨断轨应力偏大，钢轨在左侧梁端处断开引起的右侧梁端处钢轨应力值为86．8 MPa，梁格模型为61．4 MPa．

钢轨在不同位置断开引起的钢轨纵向位移变化规律基本一致，但在两处折断处产生的断缝宽度有所不同，且梁格模型计算结果偏大．梁格模型在接近固定支座的梁端处断开引起的断缝宽为56．7mm，平面模型为50．4mm；梁格模型在远离固定支座的梁端处断开引起的断缝宽为54．9mm，平面模型为48．9mm．钢轨在接近固定支座的梁端处断开引起的断缝更明显．

断轨作用下，梁格模型和平面模型计算所得的最大墩顶水平力分别为975．4kN 和690．9kN．

4 结 论

1）本文所建立的拱加劲连续梁桥与双线轨道相互作用的梁格模型比平面模型更精细，比实体模型更简洁，能够准确反映桥上无缝线路受力的空间特性，具有较强的适用性．

2）梁格模型和平面模型中钢轨伸缩应力和断轨应力的变化规律基本一致，但平面模型计算结果偏大．平面模型计算所得的最大伸缩压应力比梁格模型偏大约10．5%；平面模型中钢轨在一侧梁端断开引起的另一侧梁端处钢轨应力比梁格模型计算结果偏大约41．4%．

3）平面模型和梁格模型中钢轨挠曲应力分布规律基本一致，但平面模型最大值比梁格模型偏大约50．1%．

4）双线对向制动工况下，平面模型制动应力基本为零，梁格模型制动应力有多处峰值，平面模型无法准确模拟双线对向制动工况．

5）单线行驶时，梁格模型有载线钢轨制动应力变化趋势比无载线复杂，制动压应力均在梁端达到峰值，但有载线是无载线的1．4倍．平面模型与梁格模型有载线钢轨制动应力变化规律一致，但数值上远大于梁格模型计算结果．传统的平面模型无法准确反映桥上多线轨道的受力情况．

6）对于活载作用下大跨度多线铁路桥上无缝线路纵向力分析，建议采用本文所述的考虑轨道结构的桥梁空间梁格模型．

［1］YU Xiang－dong，WU Zhi－hua．Transverse analysis of boxgirder for continuous beam arch composite railway bridge［J］．Applied Mechanics and Materials，2013，405／408：1531－1537．

［2］易云焜，肖汝诚．均布荷载作用下梁拱组合桥梁的实用计算［J］．同济大学学报：自然科学版，2008，36（6）：728－732．

YI Yun－kun，XIAO Ru－cheng．Practical calculation of beamarch association bridge under uniform load ［J］．Journal of Tongji University：Natural Science，2008，36（6）：728－732．（In Chinese）

［3］李克银．连续梁桥荷载试验梁格法分析［J］．铁道工程学报，2011，153（6）：25－75．

LI Ke－yin．Analysis of load tests for continuous girder bridge with grillage theory［J］．Journal of Railway Engineering Society，2011，153（6）：25－75．（In Chinese）

［4］闫斌，戴公连．考虑加载历史的高速铁路梁轨相互作用分析［J］．铁道学报，2014，36（6）：75－80．

YAN Bin，DAI Gong－lian．Analysis of interaction between continuously welded rail and high－speed railway bridge considering load－history［J］．Journal of the China Railway Society，2014，36（6）：75－80．（In Chinese）

［5］于向东，沙嵩，闫斌．客货共线大跨度简支钢桁梁桥梁轨相互作用［J］．湖南大学学报：自然科学版，2014，41（6）：106－111．

YU Xiang－dong，SHA Song，YAN Bin．Track－bridge interaction of long－span simply supported steel truss bridge in mixed passenger and freight railway［J］．Journal of Hunan University：Natural Sciences，2014，41（6）：106－111．（In Chinese）

［6］YAN Bin，DAI Gong－lian．Seismic pounding and protection measures of simply－supported beams considering interaction between continuously welded rail and bridge［J］．Structural Engineering International，2013，23（1）：61－67．

［7］HU Nan，DAI Gong－lian，YAN Bin，etal．Recent development of design and construction of medium and long span high－speed railway bridges in China［J］．Engineering Structures，2014，74：233－241．

［8］UIC 774－3—2001 Track／bridge interaction recommendations for calculations［S］．Paris：International Union of Railways，2001：8－30．

［9］徐庆元，陈秀方，周小林，等．桥上无缝线路附加力计算模型研究［J］．长沙铁道学院学报，2003，21（3）：14－18．

XU Qing－yuan，CHEN Xiu－fang，ZHOU Xiao－lin，etal．Investigation on mechanics model of additional longitudinal forces transmission between continuously welded rails and bridges［J］．Journal of Changsha Railway University，2003，21（3）：14－18．（In Chinese）

［10］卜一之．高速铁路桥梁纵向力传递机理研究［D］．成都：西南交通大学土木工程学院，1998：8－10．

BU Yi－zhi．Research on the transmission mechanism of longitudinal stress for high－speed railway bridges［D］．Chengdu：College of Civil Engineering，Southwest Jiaotong University，1998：8－10．（In Chinese）

［11］徐庆元，陈秀方，周小林，等．高速铁路桥上无缝线路力学计算模型对比［J］．交通运输工程学报，2005，5（3）：19－24．

XU Qing－yuan，CHEN Xiu－fang，ZHOU Xiao－lin，etal．Mechanics computation model comparison of continuously welded rails on high－speed railway bridges［J］．Journal of Traffic and Transportation Engineering，2005，5（3）：19－24．（In Chinese）

［12］SONG M K，NOH H C，CHOI C K．A new three－dimensional finite element analysis model of high－speed train－bridge interactions［J］．Engineering Structures，2003，25（13）：1611－1626．

［13］TB 10015－2012铁路无缝线路设计规范［S］．北京：中国铁道出版社，2013：8－17．

TB 10015－2012Code for design of railway continuously welded rail ［S］．Beijing：China Railway Publishing House，2013：8－17．（In Chinese）

［14］张学龙．小箱梁的梁格划分及虚拟横梁刚度分析研究［D］．西安：长安大学公路学院，2013：8－12．

ZHANG Xue－long．Study and analysis on beam meshing and the virtual beam stiffness of small box girder［D］．Xi’an：School of Highway，Chang’an University，2013：8－12．（In Chinese）

［15］吴烨．预应力混凝土连续宽箱梁纵横向分析［D］．上海：同济大学土木工程学院，2009：23－31．

WU Ye．Longitudinal and transverse analysis for prestressed concrete continuous beam bridges［D］．Shanghai：College of Civil Engineering，Tongji University，2009：23－31．（In Chinese）