圆钢管混凝土短柱的火灾后剩余承载力研究

李 毅，王志滨

（福州大学 土木工程学院，福建 福州 350108）

随着钢管混凝土结构的广泛应用和高层建筑火灾事故的日益增多，钢管混凝土结构的抗火性能研究越来越受到人们的重视，对火灾后钢管混凝土柱残余力学性能的研究也在不断深入．霍静思等［1］对高温后钢管混凝土抗冲击性能进行了试验研究；Han和Huo［2］提出了未受初始荷载的火灾后钢管混凝土长柱的剩余承载力简化计算方法；Yang等［3］采用纤维模型法对钢管混凝土长柱进行了火灾全过程分析，提出了适用于存在初始荷载作用的火灾后钢管混凝土长柱剩余承载力的预测方法．轴压短柱是建筑结构中的基本构件之一，林晓康［4］和余鑫［5］对火灾后的钢管混凝土轴压短柱进行了试验研究；Han等［6］和Tao等［7］报道了火灾后的轴压短柱试验；Huo等［8］对承受初始荷载的圆钢管混凝土轴压短柱在经历恒高温作用后的力学性能进行了试验研究；Song等［9］采用顺序耦合的热－应力分析方法对钢管混凝土轴压短柱进行了火灾全过程分析．试验研究和理论分析的最终目的是为工程设计提供可靠参考，而对于如何评估火灾后轴压短柱的剩余承载能力，目前尚未见相关报道．

本文采用有限元软件ABAQUS对圆钢管混凝土轴压短柱进行火灾全过程分析，采用完全耦合的热－力分析模块建立考虑火灾全过程影响的圆钢管混凝土轴压短柱的有限元计算模型，对火灾全过程中圆钢管混凝土轴压短柱的工作机理进行深入研究，对火灾后圆钢管混凝土轴压短柱剩余承载力的影响参数进行比较分析，最后提出火灾后圆钢管混凝土轴压短柱剩余承载力的简化计算方法．

1 有限元计算模型

1．1 温度作用曲线

目前火灾试验多采用国际标准化组织建议的ISO－834室内环境温度曲线［10］，如图1所示，th为升温时间，根据实际火灾情况确定，tp为室内温度降至常温的时间．标准化室内环境温度曲线虽不能真实反映火灾全过程中室内环境温度的变化，但可为结构抗火研究提供统一标准，使大量火灾试验结果具有可比性．

ISO－834室内环境温度曲线中未给出火灾后构件内部温度恢复至常温的终点时刻tr，在采用有限元软件ABAQUS 计算构件截面温度场时发现，构件内部温度的变化不仅与室内环境温度变化有关，还与构件截面尺寸及防火保护层厚度有关．本文根据有限元计算结果，以升温时间、截面尺寸和防火保护层厚度为自变量，通过多元非线性回归得到了tr的计算公式如下：

式中：k1，k2，k3，k4，k5，k6，k7，k8，k9，k10为固定系数，k1＝－6．77×10－8，k2＝－7．03×10－6，k3＝1．96×10－5，k4＝2．59×10－3，k5＝1．96，k6＝－8．83×10－5，k7＝8．18×10－4，k8＝0．167；k9＝3．24，k10＝19；D为截面直径，mm；a为防火保护层厚度，mm；th为升温时长，min；式（1）的适用范围截面：圆钢管混凝土的直径D＝100～1 200mm；截面含钢率α＝0．05～0．15；厚涂型钢结构防火保护层厚度a＝0～30mm；ISO－834标准火灾的受火时间t＝0～3h．

图1 ISO－834室内环境温度全曲线Fig．1 ISO－834standard temperature curve of full range fire

1．2 材料本构

1．2．1 钢材

钢材的热工性能采用EC3［11］建议的热工参数模型．常温下钢材的弹性模量取为2．06GPa，泊松比取为0．3．李国强等［12］认为钢材的泊松比受温度的影响很小，高温中泊松比与温度变化无关．丁发兴等［13］的实测结果表明钢材弹性阶段的泊松比与常温下的泊松比相当接近．因此，钢材在火灾全过程中的泊松比均取为0．3．

1）高温中钢材的应力－应变关系模型数学表达式如下：

式中：Es，h，fy，h，fu，h分别为高温中钢材的弹性模量、屈服强度、极限强度；εy，h，εh，h，εu，h分别为高温中钢材的屈服应变、硬化应变、极限应变，εy，h＝fy，h／Es，h；p为强化段有关的强化参数．各参数取值方法如下：

式中：T为升温阶段材料积分点的当前温度，℃，当T为常温时，即为常温下钢材的应力－应变关系；Es，fy，fu分别为常温下钢材的弹性模量、屈服强度、极限强度；εy，εh，εu分别为常温下钢材的屈服应变、强化应变、极限应变，εy＝fy／Es；fu，εh，εu计算式如下：

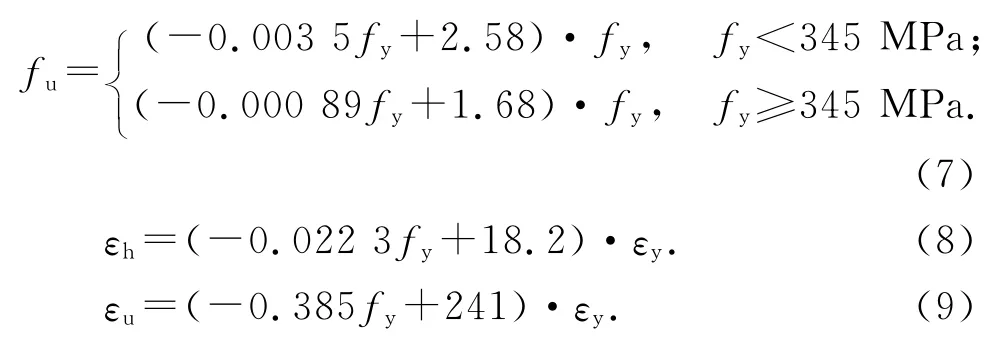
2）高温冷却后钢材的应力－应变关系模型数学表达式与高温中的相同，见式（2），只需将表达式中的Es，h，fy，h，fu，h，εy，h，εh，h，εu，h替换成其中高温冷却后的弹性模量Es，p，屈服强度fy，p，极限强度fu，p，屈服应变εy，p，硬化应变εh，p，极限应变εu，p，其中εy，h＝fy，p／Es，p，强化参数p取为3．5．

式中：Tmax为材料积分点在火灾全过程中经历的最高温度，℃，当Tmax为常温时，即为常温下钢材的应力－应变关系．

3）降温阶段钢材的弹性模量、屈服应力和强化段的应力值以降温阶段的当前温度为自变量在升温阶段和高温冷却后阶段之间线性插值获得，具体计算表达式如下：

式中：εy，c（T，Tmax）为降温过程中钢材的屈服应变，

Es，c（T，Tmax）为降温过程中钢材的弹性模量，

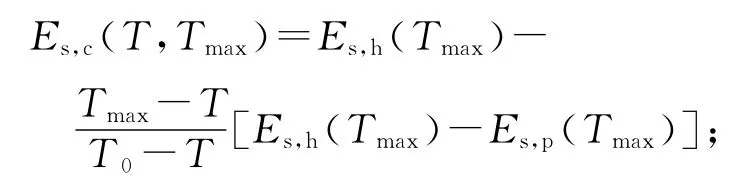
fy，c（T，Tmax）为降温过程中钢材的弹性模量，

Es，h（Tmax），fy，h（Tmax）和σh（Tmax）分别为高温中钢材的弹性模量、屈服应力和强化段应力；

Es，p（Tmax），fy，p（Tmax）和σp（Tmax）分别为高温后钢材的弹性模量、屈服应力和强化段应力．

1．2．2 核心混凝土

核心混凝土的热工性能采用EC2［14］中的热工参数模型．核心混凝土采用塑性损伤模型来定义；Tao等［15］采用ABAQUS对大量钢管轴压短柱的试验数据进行试算分析，提出了常温下核心混凝土的应力－应变关系；Tao等［15］采用的常温下钢材应力－应变关系也与本文建议的钢材应力－应变关系类似；因此常温下核心混凝土应力－应变关系采用该模型，具体计算表达式见Tao等［15］所述．

基于Tao等［15］提出的常温下核心混凝土的应力－应变关系模型，王勇等［16］对弹性模量、峰值应力、峰值应变和应力－应变关系下降段进行修正，建议了高温中核心混凝土的应力－应变关系．高温中圆柱体抗压强度采用EC2［14］中的建议值，高温中弹性模量和峰值应变计算公式如下．

弹性模量：

峰值应变：

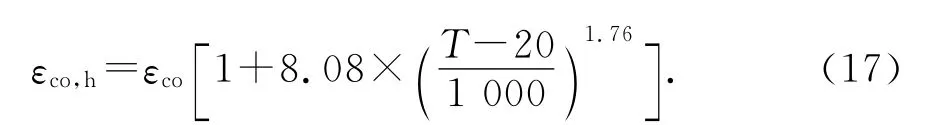
式中：Ec为常温下混凝土的弹性模量；εco为常温下素混凝土的峰值应变．

高温中钢材的受热膨胀使钢管与核心混凝土之间逐渐产生分离，导致钢管对核心混凝土的约束作用逐渐降低，可以通过对约束效应系数中的钢管屈服强度进行折减来反映高温中钢管对核心混凝土约束效应的降低：

式中：As和Ac分别为钢管和核心混凝土的截面面积；f′c为常温下圆柱体轴心抗压强度；fy，h为高温中钢管的屈服强度，按表1确定，800 ℃以上取800 ℃时的值．

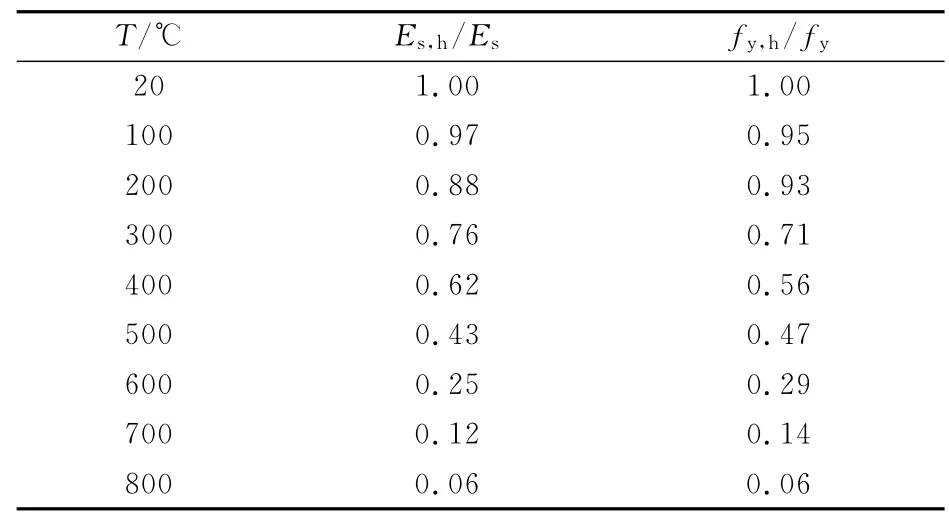
表1 高温中钢材弹性模量和屈服强度的折减系数Tab．1 Reduction factor of Es，hand fy，hat elevated temperatures

高温冷却后的核心混凝土的应力－应变关系同样采用上述方法来确定，高温冷却后圆柱体抗压强度按表2确定．

表2 高温冷却后圆柱体抗压强度的折减系数Tab．2 Reduction factor of cylinder compressive strength after exposure to elevated temperatures

高温冷却后弹性模量和峰值应变的计算公式如下，式中fcu为常温下混凝土立方体抗压强度．

弹性模量：

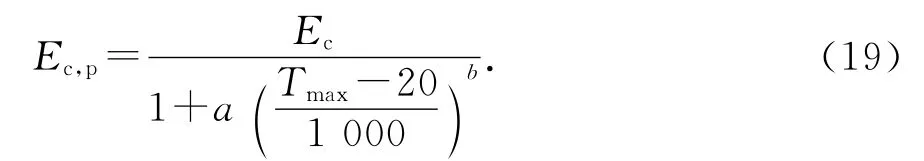
式中：a＝－0．37·fcu＋46．2；b＝－0．02·fcu＋3．68．

峰值应变：

高温冷却后钢管屈服强度基本恢复至常温水平，高温冷却后的约束效应系数采用常温下的值．常温下泊松比取0．2；高温对混凝土的泊松比存在显著的影响，高温中混凝土的泊松比在150 ℃时开始减小，400 ℃时减小为常温下的50%，1 200 ℃时 接近为0［17］；假定降温阶段和高温冷却后混凝土泊松比并未得到恢复，降温阶段和高温冷却后混凝土的泊松比采用高温中的值．

核心混凝土的受拉性能选用开裂应力－断裂能关系的能量破坏准则来定义，常温下混凝土的开裂应力和断裂能的取值参考Tao等［15］．假定高温中、降温阶段和高温冷却后混凝土的断裂能取值与常温下相同．以下公式中，ft为常温下混凝土抗拉强度．

高温中混凝土抗拉强度：

高温冷却后混凝土抗拉强度：

降温阶段核心混凝土应力－应变关系模型的确定，同样可以采用与确定钢材降温阶段应力－应变关系模型相同的方法，即降温阶段混凝土的弹性模量、弹性段结束处的应力值和弹性段以后的应力值以降温阶段的当前温度为自变量在升温阶段和高温冷却后阶段之间线性插值获得．

1．2．3 材料模型转换

在火灾全过程中，构件内部材料积分点处于不同温度阶段时需赋予不同的材料属性，可通过设置场参数（Field）和调用场变量子程序（USDFLD）来实现，例如：升温阶段的场参数取为0，高温冷却后阶段的场参数取为1，降温阶段的场参数可以根据降温阶段的当前温度在常温和升温阶段最高温度之间所处的位置，在0～1之间进行线性插值．材料积分点所处的温度阶段，可以通过当前增量步温度Tt与前一步增量步温度Tt－Δt的大小比较以及当前荷载步来综合判断，如图2所示．

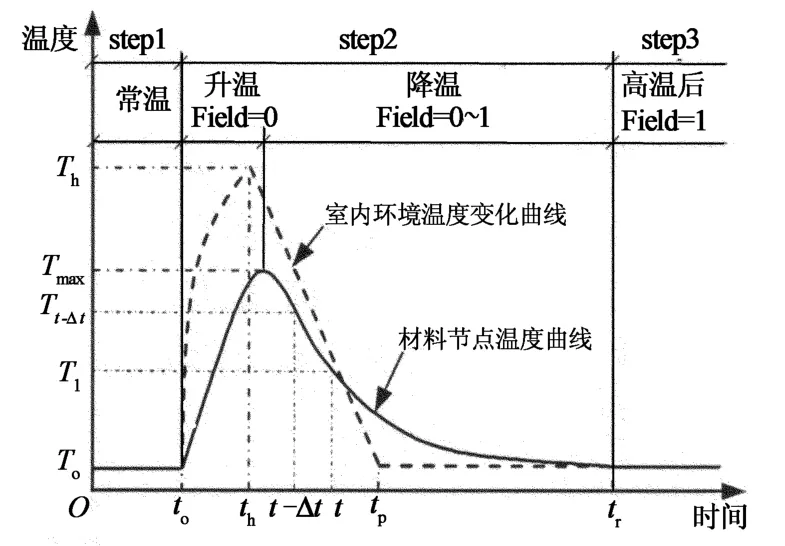
图2 材料积分点所处温度阶段的判断Fig．2 Determining temperature phase of integration points

1．2．4 防火涂料

采用厚涂型钢结构防火保护涂料，其导热系数为0．116W／（m·℃），比热为1 047J／（kg·℃），密度为（400±20）kg／m3．厚涂型防火保护涂料的抗压强度只为0．3～1．2 MPa［12］，因此可认为厚涂型防火保护涂料不参与结构受力．

1．3 接触关系

构件表面与环境之间的辐射和对流系数取值参考EC1［18］．假设防火保护层与钢管之间的接触紧密，而对于钢管与核心混凝土表面之间的接触传热行为，本文基于Ghojel［19］提出的接触热阻计算公式，建议了受载情况下的圆钢管与核心混凝土之间接触热导的计算公式如下：

式中：kR为接触热导，是接触热阻R的倒数；Ts为钢管温度，a＝160．5，b＝63．8，c＝339．9，d＝－1．4．

钢管与核心混凝土之间采用面－面接触来模拟，法向为“硬”接触，允许接触面之间相互脱离，切向采用库仑摩檫模型，摩擦因数取为0．6．防火保护层与钢管之间关系采用绑定约束（Tie）来模拟．

1．4 单元选取与加载方式

钢管采用四节点缩减积分格式热力耦合的壳单元（S4RT），防火保护层采用四节点完全积分格式热力耦合的壳单元（S4T），核心混凝土采用八节点线性缩减积分热力耦合的三维实体单元（C3D8RT）．

在上下两个端面的中心位置各设一个参考点（Reference Point），端面上钢管和混凝土节点与参考点耦合在一起，约束下端面参考点的所有自由度，约束上端面参考点除轴向位移以外的所有自由度．火灾前施加轴向荷载，火灾中轴向荷载保持恒定，火灾后进行轴向位移加载．由于构件几何尺寸以及边界条件的对称性，采用1／8模型进行计算．

2 模型验证与机理分析

2．1 有限元模型验证

图3给出了圆钢管混凝土截面温度场变化的有限元计算曲线和实测曲线的比较，可以看出，本文的有限元计算模型不仅能较好地计算出圆钢管混凝土在升温阶段的截面温度场，而且对于火灾全过程温度场的计算，也能取得很好的计算效果．

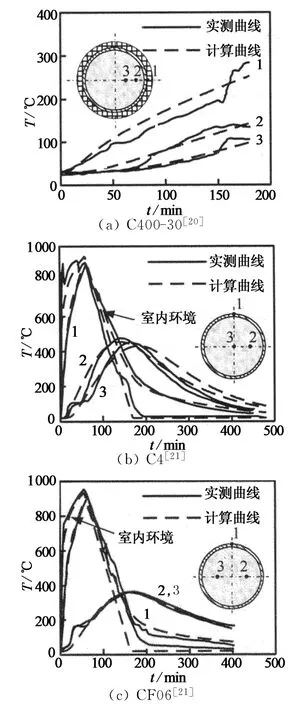
图3 温度场的计算曲线和实测曲线比较Fig．3 Comparisons between calculated and experimental temperature－time curves

图4给出了圆钢管混凝土柱在升温阶段的轴向位移－受火时间关系的有限元计算曲线和实测曲线比较，通过比较验证了升温阶段材料模型的适用性．图5给出了火灾后圆钢管混凝土轴压短柱的荷载－平均纵向应变关系的有限元计算曲线和实测曲线比较，通过比较验证了本文有限元模型计算火灾后圆钢管混凝土轴压短柱剩余承载力的准确性．

图5还给出了未考虑火灾全过程影响的荷载－平均纵向应变关系曲线，即图中“未考虑”表示的曲线．从图中可以看出，未考虑火灾全过程影响的承载力要比考虑火灾全过程影响的低．未考虑火灾全过程影响的分析方法只能计算出火灾后的荷载－平均纵向应变关系曲线，而无法对构件在升温和降温阶段的受力性能进行分析．

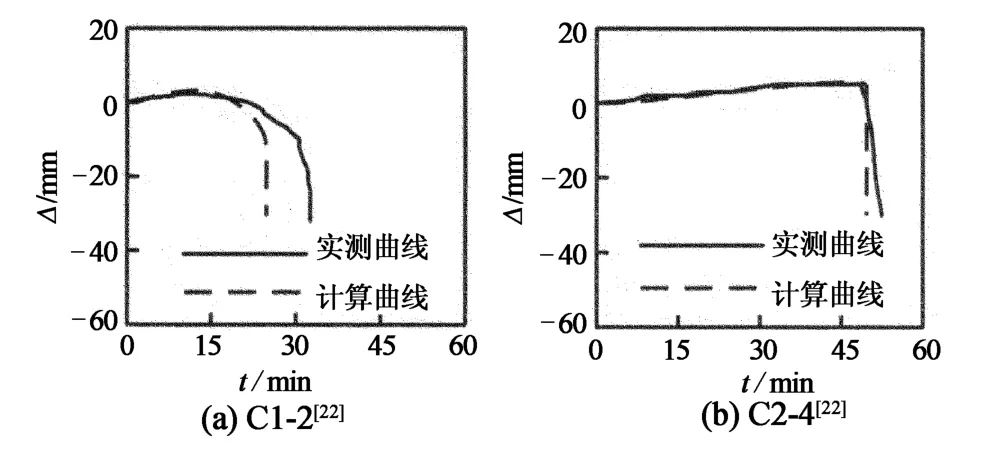
图4 火灾下耐火性能的计算曲线和实测曲线比较Fig．4 Comparisons between calculated and experimental curves of fire resistance

图5 火灾后荷载－变形关系的计算曲线和实测曲线比较Fig．5 Comparisons between calculated and experimental load－deformation curves after fire

2．2 工作机理分析

采用典型算例对圆钢管混凝土轴压短柱在火灾全过程中的工作机理进行分析：构件截面直径D＝300mm，钢管厚度t＝7mm，构件长度L＝3D，钢材强度fy＝345 MPa，混凝土强度fcu＝50 MPa，含钢率α＝0．1，约束效应系数x＝1，轴压比n＝0．4，防火保护层厚度a＝20mm，ISO－834标准火灾升温时长t＝3h（180min），构件四周均匀受火，室温To＝20 ℃．

2．2．1 荷载－变形关系全曲线

图6为火灾全过程中荷载（N）－变形（ε）关系全曲线，其中变形为平均纵向应变ε＝Δ／L，Δ为构件的轴向变形，L为构件的长度．图中关键点的含义如下：A 点为构件加载至初始荷载时，B点为室内环境温度升至最高温度时，C 点为构件轴向伸长变形最大时，D 点为室内环境温度恢复至常温时，E 点为构件内部温度恢复至常温时，F 为火灾后构件继续加载至极限承载力时．所以火灾全过程荷载－变形关系曲线可分为以下几个阶段：

AB段：施加轴向荷载，构件产生了初始轴向压缩变形，荷载－变形关系曲线基本呈线性．

BC段：轴向荷载保持恒定，室内环境温度开始升高，构件受热膨胀，材料随着温度升高逐渐劣化，当室内环境温度达到最大值时，构件的平均纵向应变表现为拉应变．

CM 段：室内环境温度开始下降，构件内部的温度还在升高，轴向膨胀继续发展，而材料劣化导致的轴向压缩变形并不足以抵消受热膨胀作用产生的轴向伸长变形，所以构件的轴向膨胀仍然有所发展，轴向伸长达到最大值，荷载－变形关系曲线上表现为平均纵向拉应变达到最大值．

MD 段：室内环境温度继续下降，但构件内部的温度并未整体开始降低，材料劣化导致的轴向压缩变形逐渐抵消了温度膨胀作用产生的轴向伸长变形，构件轴向伸长量开始减小．当室内环境温度降至常温时，构件的平均纵向应变仍为拉应变．

DE段：室内环境温度已降至常温，构件内部温度开始逐渐降低，降温导致构件产生收缩变形，构件的平均纵向应变由拉应变为压应变，直至构件内部完全恢复至常温，仍存在残余轴向压缩变形．

EF段：继续对构件进行加载至极限承载力Nr（其中Nr取值方法为：构件内部完全恢复至常温后从E点完全卸载，然后从A′重新加载，在平均纵向应变增长到10 000με前，荷载－平均纵向应变关系曲线出现下降段的取峰值荷载为极限承载力，未出现下降段的取10 000με对应的荷载为极限承载力）．

图6 典型火灾全过程中的荷载－变形关系曲线Fig．6 Typical load－deformation curves during an entire fire exposure

2．2．2 核心混凝土和钢管的应力分析

图7为火灾全过程中荷载－变形关系全曲线上关键点对应中截面上的核心混凝土和钢管的温度场和应力场．

B点处：常温下对构件施加了初始轴向荷载，产生了初始应力场，核心混凝土的纵向应力为0．5f′c，钢管的纵向应力为0．41fy．

C点处：室内环境温度升至最高温度，钢管温度达到371℃，核心混凝土的温度由外向内逐渐降低，中心区域的温度只有170℃；受热膨胀量较大，钢管和核心混凝土外围承担着更多荷载，核心混凝土外围的纵向应力最大达到0．6f′c，中心区域的纵向应力几乎降至0，钢管的纵向应力增大到0．69fy．

M 点处：构件轴向伸长达到最大，室内环境处在降温中，钢管温度有所升高，达到417 ℃，核心混凝土的温度也继续升高，尤其中心区域的温度达到301 ℃，导致中心区域分担更多的荷载，核心混凝土中心区域的纵向应力达到0．26f′c；核心混凝土外围的纵向应力减小至0．54f′c，钢管的纵向应力减小至0．55fy．

D 点处：室内环境温度降至常温，构件内部还存在较高的温度场，钢管温度降至335℃，而核心混凝土中心区域的温度升高到了363 ℃，中心区域承担的荷载继续增大，纵向应力达到0．63f′c；核心混凝土外围和钢管的膨胀量减小，其承担的荷载有所降低，核心混凝土外围的纵向应力减小至0．36f′c，钢管的纵向应力减小至0．46fy．

E点处：构件内部温度恢复至常温，火灾中核心混凝土中心区域经历的温度较低，火灾后材料劣化程度低于核心混凝土外围，所以核心混凝土中心区域将承担更多的荷载，核心混凝土中心区域的纵向应力升至0．71，核心混凝土外围的纵向应力降至0．35f′c；钢管虽然在火灾中经历的温度最高，但火灾后钢管材性基本能恢复至火灾前的水平，所以钢管的纵向应力仍维持在0．46fy左右．

F点处：火灾后继续加载至极限荷载，整个截面的纵向应力都有很大增长，钢管的纵向应力达到0．86fy，同时由于外钢管对核心混凝土约束作用的发挥，核心混凝土外围的纵向应力达到0．98f′c，核心混凝土中心区域的纵向应力达到1．10f′c．

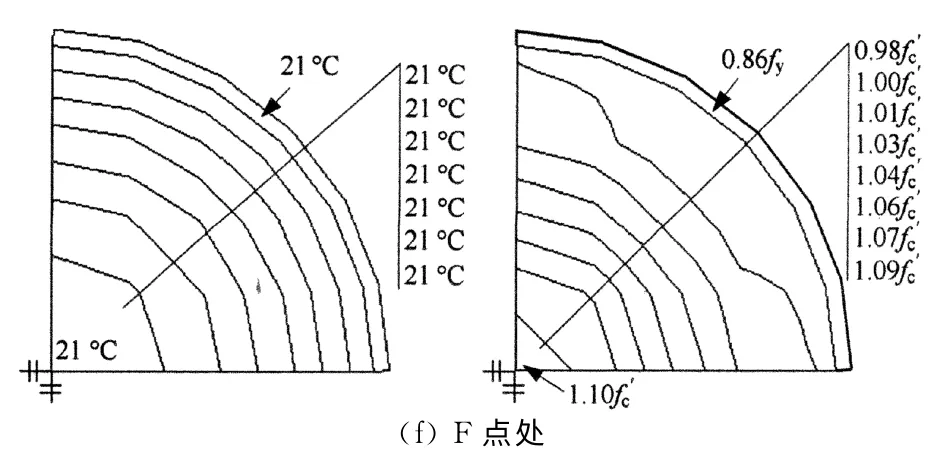
图7 关键点处核心混凝土和钢管的温度场和应力场Fig．7 Distribution of temperature and longitudinal stress in concrete core and steel tube at typical points

2．2．3 钢管和核心混凝土的相互作用

图8为火灾全过程中构件中截面处钢管与核心混凝土相互作用力的变化情况．从图中可以看出：火灾中（0至tp之间），由于钢管的横向膨胀变形大于核心混凝土，从而导致钢管与核心混凝土界面产生分离，所以两者的相互作用力为零；在室内环境温度恢复至常温后（tp之后），钢管和核心混凝土相接触，两者产生了相互作用力，但作用力较小；火灾后继续进行加载（tr之后），如图8所示，钢管和核心混凝土之间的相互作用力迅速增长．这说明，火灾中钢管对核心混凝土几乎不存在约束作用，室内环境温度降至常温后，钢管才开始对核心混凝土产生约束作用．

图8 钢管和核心混凝土之间的相互作用Fig．8 Interactions between steel tube and concrete core

3 剩余承载力简化计算

3．1 参数分析

影响圆钢管混凝土轴压短柱剩余承载力的可能参数主要有：钢材强度、混凝土强度、截面含钢率、轴压比、受火时间、防火保护层厚度和截面尺寸．为了便于比较分析，定义火灾全过程作用后的圆钢管混凝土轴压短柱的剩余承载力影响系数：

式中：Nu为未受火钢管混凝土轴压短柱在常温下的极限承载力；Nr为火灾后钢管混凝土轴压短柱的剩余承载力．

图9 为参数变化对剩余承载力影响系数的影响，从图中可以看出：钢材强度的变化不会对kr造成影响；混凝土抗压强度在60 MPa以下变化对kr影响甚微，混凝土抗压强度达到80 MPa时，kr有小幅度降低；含钢率大于0．1时，该参数对kr的影响较小；含钢率为0．05时，kr有小幅度降低；轴压比为0．2和0．4时的kr比轴压比为0和0．6时的略小，可见轴压比变化对kr影响也不大，这与Huo等［8］的试验结论相一致；kr随受火时间的增加而明显减小；kr随防火保护层厚度和截面尺寸的增大而显著提高；可见防火保护层不仅能提高构件的耐火性能，还能提高火灾后构件的承载能力，火灾作用对截面尺寸较大构件所造成的承载能力损失较小．

3．2 简化计算公式

基于上述参数分析可以确定，对圆钢管混凝土轴压短柱剩余承载力影响较大的参数有：受火时间、防火保护层厚度和截面直径．以t，a和D为自变量，以kr为因变量，通过多元非线性回归得到剩余承载力影响系数kr的具体计算公式如下．

式中：fr＝f（to）·f（ao）·f（Do）；

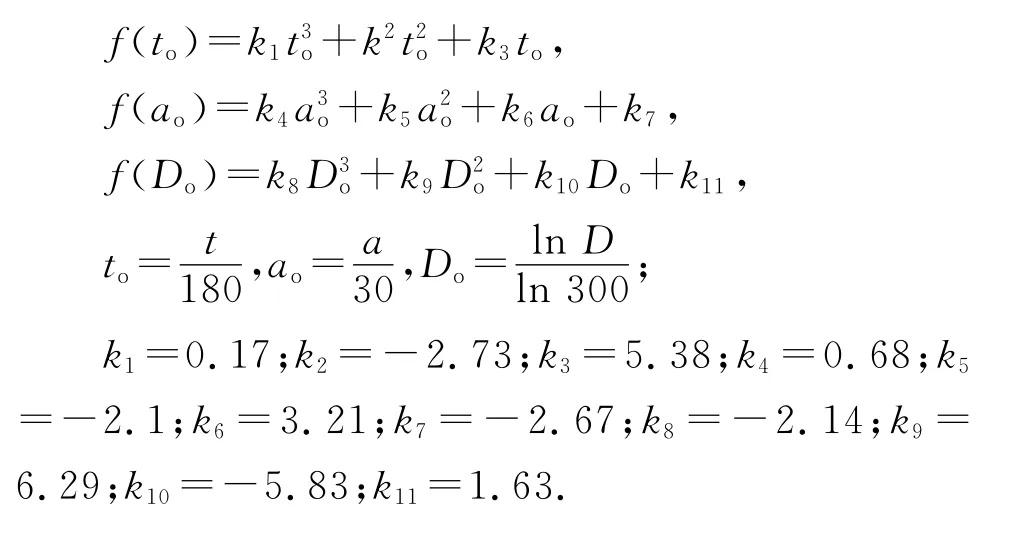
图9 各参数对剩余承载力影响系数的影响Fig．9 Influence of different parameter on residual strength index

公式适用范围：截面直径D＝100～1 200mm；Q235～Q490 钢；C30～C80 混凝土；α＝0．05～0．15；厚涂型钢结构防火保护层厚度a＝0～30 mm；轴压比n＝0～0．6；受火时间t＝0～3h．只要给定圆钢管混凝土短柱的截面尺寸、防火保护层厚度和受火时间，即可根据式（25）求出火灾全过程作用后圆钢管混凝土轴压短柱的剩余承载力：

式中未受火圆钢管混凝土轴压短柱的极限承载力Nu根据福建省工程建设标准DBJ／T13－51－2010［23］中的计算公式求得．

图10给出了按式（25）和（26）得到的简化计算结果和有限元计算结果的比较，可见简化计算结果与有限元计算结果基本吻合，拟合偏差控制在±10%．

图11给出了按式（25）和（26）得到的简化计算结果和试验结果的比较情况，计算值（Nuc）与试验值（Nue）之比的平均值为0．920，均方差为0．127．

图10 简化计算结果与有限元计算结果比较Fig．10 Comparison of calculated residual strength index between simplified formula and finite element model

图11 简化计算结果与试验结果比较Fig．11 Comparison of calculated residual strength between simplified formula and tests

4 结 论

1）采用本文提出的高温中、高温后以及降温阶段的钢材和核心混凝土应力－应变关系，基于完全耦合的热－力分析方法对圆钢管混凝土轴压短柱进行火灾全过程分析是可行的．

2）火灾全过程中核心混凝土和钢管的纵向应力分布主要与截面温度场分布有关．火灾中钢管与核心混凝土之间产生分离，钢管对核心混凝土的约束作用消失；当室内环境温度降至常温后，钢管开始对核心混凝土产生约束作用．

4）影响火灾后圆钢管混凝土轴压短柱剩余承载力的主要参数为：受火时间、防火保护层厚度和截面尺寸．

5）按本文提出的简化计算公式计算的结果与试验结果基本吻合，可为有关工程设计提供参考．

［1］霍静思，何远明，肖莉平，等．高温后钢管混凝土抗多次冲击力学性能试验研究［J］．湖南大学学报：自然科学版，2012，39（9）：6－10．

HUO Jing－si，HE Yuan－ming，XIAO Li－ping，etal．Experimental study on the dynamic behavior of concrete－filled steel tube after exposure to high temperatures under multiple impact loadings［J］．Journal of Hunan University：Natural Sciences，2012，39（9）：6－10．（In Chinese）

［2］HAN L H，HUO J S．Concrete－filled hollow structural steel columns after exposure to ISO－834fire standard［J］．Journal of Structural Engineering，2003，129（1）：68－78．

［3］YANG H，HAN L H，WANG Y C．Effects of heating and loading histories on post－fire cooling behaviour of concrete－filled steel tubular columns［J］．Journal of Constructional Steel Research，2008，64（5）：556－570．

［4］林晓康．火灾后钢管混凝土压弯构件的滞回性能研究［D］．福州：福州大学土木工程学院，2006：43－47．

LIN Xiao－kang．Cyclic performance of concrete－filled steel tubular columns after exposure to fire［D］．Fuzhou：College of Civil Engineering，Fuzhou University，2006：43－47．（In Chinese）

［5］余鑫．标准火灾作用后新型组合结构柱的力学性能研究［D］．福州：福州大学土木工程学院，2010：19－21．

YU Xin．Behavior of innovative composite columns after exposure to standard fire［D］．Fuzhou：College of Civil Engineering，Fuzhou University，2010：19－21．（In Chinese）

［6］HAN L H，HUO J S，WANG Y C．Compressive and flexural behaviour of concrete filled steel tubes after exposure to standard fire［J］．Journal of Constructional Steel Research，2005，61（7）：882－901．

［7］TAO Z，HAN L H，WANG L L．Compressive and flexural behaviour of CFRP－repaired concrete－filled steel tubes after exposure to fire［J］．Journal of Constructional Steel Research，2007，63（8）：1116－1126．

［8］HUO J S，HUANG G W，XIAO Y．Effects of sustained axial load and cooling phase on post－fire behaviour of concrete－filled steel tubular stub columns［J］．Journal of Constructional Steel Research，2009，6（5）：1664－1676．

［9］SONG T Y，HAN L H，YU H X．Concrete filled steel tube stub columns under combined temperature and loading［J］．Journal of Constructional Steel Research，2010，66（3）：369－384．

［10］ISO－834Fire－resistance tests—elements of building construction—Part1：general requirements［S］．Geneva：International Organization for Standardization，1999：12－13．

［11］European Code 3 Design of steel structures Part 1－2：general rules—structural fire design［S］．Brussels，Belgium：CEN，2005：22－26．

［12］李国强，韩林海，楼国彪，等．钢结构及钢－混凝土组合结构抗火设计［M］．北京：中国建筑工业出版社，2006：107．

LI Guo－qiang，HAN Lin－hai，LOU Guo－biao，etal．Fire－resistance design of steel and steel－concrete composite structures［M］．Beijing：China Architecture ＆Building Press，2006：107．（In Chinese）

［13］丁发兴，余志武，温海林．高温后Q235钢材力学性能试验研究［J］．建筑材料学报，2006，9（2）：245－249．

DING Fa－xing，YU Zhi－wu，WEN Hai－lin．Experimental research on mechanical properties of Q235steel after high temperature treatment［J］．Journal of Building Materials，2006，9（2）：245－249．（In Chinese）

［14］European Code 2Design of concrete structures Part 1－2：General rules－structural fire design［S］．Brussels，Belgium：CEN，2004：26－29．

［15］TAO Z，WANG Z B，YU Q．Finite element modelling of concretefilled steel tubular columns under axial compression［J］．Journal of Constructional Steel Research，2013，89（10）：121－131．

［16］王勇，董毓利，袁广林，等．考虑瞬态热应变的钢筋混凝土板火灾反应分析［J］．湖南大学学报：自然科学版，2014，41（6）：63－69．

WANG Yong，DONG Yu－li，YUAN Guang－lin，etal．Fire response analysis slabs considering of reinforced concrete transient strain［J］．Journal of Hunan University：Natural Sciences，2014，41（6）：63－69．（In Chinese）

［17］IZZUDDIN B A，ELGHAZOULI A Y，TAO X Y．Realistic modeling of composite floor slabs under fire conditions［C］／／Proceedings of 15th ASCE Engineering Mechanics Conference．New York：Columbia University，2002：777－785．

［18］European Code 1 Actions on structures—Part 1－2：general actions—actions on structures exposed to fire［S］．Brussels，Belgium：CEN，2002：24－25．

［19］GHOJEL J．Application of inverse analysis to thermal contact resistance between very rough nonconforming surfaces［J］．Inverse Problems in Engineering，2002，10（4）：323－334．

［20］HAN L H，XU L，ZHAO X L．Tests and analysis on the temperature field within concrete－filled steel tubes with or without protections subjected to a standard fire［J］．Advances in Structural Engineering，2003，6（2）：121－133．

［21］HUO J S，ZENG X，XIAO Y．Cyclic behaviours of concrete－filled steel tubular columns with pre－load after exposure to fire［J］．Journal of Constructional Steel Research，2011，67（4）：727－739．

［22］HAN L H，ZHAO X L，YANG Y F，etal．Experimental study and calculation of fire resistance of concrete－filled hollow steel columns［J］．Journal of Structural Engineering，ASCE，2003，129（3）：346－356．

［23］DBJ／T 13－51—2010钢管混凝土结构技术规程［S］．福州：福建省住房和城乡建设厅，2010：11－12．

DBJ／T 13－51－2010Technical specification for concrete－filled steel tubular structures［S］．Fuzhou：The Housing and Construction Department of Fujian Province，2010：11－12．（In Chinese）