基于自适应层数分解的小波变换滤除冲击信号*
王 锴,刘志国†,刘 刚,易龙涛,陈 曼,彭诗棋
(1.北京师范大学 核科学与技术学院,北京 100875;2.中国石油大学(华东)石油工程学院,山东 青岛 266580)
冲击信号在机械振动中是一种常见的特征信号[1-2],具有持续时间短,衰减快,能量在广阔的频率范围内发散等特点,发生冲击振动的同时往往还包含其他重要微弱振动信息,微弱的振动信号容易被冲击信号淹没,不易识别[3].因此为了有效提取淹没在冲击信号中的微弱振动信号,滤除冲击信号显得尤为重要.
时频分析是信号分析的传统方法,频谱分析是以傅里叶变换为基础的经典谱分析和非傅里叶变换分析为基础的现代谱分析,时频分析方法已经广泛应用于非平稳信号分析.针对掺杂冲击的典型非平稳振动信号[4-5],小波变换具有优越的时频局部化分析和细化能力,改变了传统傅里叶变换不能在时域局部化的缺陷,可以迅速聚焦到信号任意频段细节,准确提取特征信号进行分析.
利用长时间进行低频局部化处理,短时间进行高频局部化处理,这种自适应窗口分析的能力改进了短时傅里叶分析方法中时频分辨率固定的不足.根据时域卷积,频域相乘原理和自适应的多分辨率特征,小波变换已经成为研究非线性非平稳信号的重要工具[6-7].
谭继勇等[8]针对冲击信号的检测问题,提出了一种冲击信号的自适应随机共振检测算法,该算法将加权鞘度指标与变尺度随机共振相结合,可以有效对微弱冲击信号进行检测,对提取冲击信号特征的自适应算法有一定参考价值.滕军等[9]针对常见的噪声信号提出了一种基于中值滤波与小波阈值降噪相结合的分解层数自适应算法,通过确定各层阈值的取值方法,有效提取淹没在噪声中的信号.本文基于滤除冲击提取有效微弱信号实验为背景,针对小波在信噪分离,提取微弱信号和突变点信号优势[10],结合冲击信号特征,合理选择小波基函数,提出了一种滤除冲击有效提取淹没信号的自适应层数分解的小波变换分析方法.
1 小波分析滤除冲击信号原理
1.1 小波变换定义
信号或函数f(t)∈L(R),与小波基进行卷积计算,可得连续小波变换[11],其表达式为:
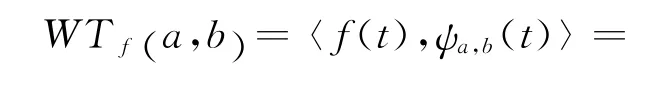

式中:a为尺度因子(a>0);b为时移因子,可正可负;WTf(a,b)为小波变换系数;Ψ a,b(t)为小波母函数;f(ω),Ψ(ω)分别为f(t),Ψ(t)的傅立叶变换.母函数在t=b处通过尺度a变换可得,其变换原理如图1所示.镜头相当于Ψ(t)起的作用.a相当于镜头向f(t)推近或远离,推近时为高频分析,远离时为低频分析.b相当于镜头相对f(t)平行移动.结合这2 个参数的调整,就可以在不同的频率尺度上进行不同的时间分析.

图1 小波变换作用原理Fig.1 Wavelet transform theory
利用尺度因子a和时移因子b,对连续小波函数Ψ a,b(t)进行离散化处理,可得离散小波函数,并推导出相应的离散小波变换表达式,再利用时移因子对时间轴归一化处理后,即得到相应的二进制离散小波变换.在具有时移不变和双尺度特性的函数空间里,由多分辨率分析可得低通平滑尺度函数Φ(t)和高通细节小波函数Ψ(t)的双尺度差分方程为:

式中:h0,k为尺度系数;h1,k为小波系数;h0,k,h1,k为共轭正交滤波器系数.先通过尺度函数Φ(t)的傅里叶变换得出H(ω),再通过无穷乘积定义Φ(ω),使Φ(t-k)具有标准正交条件,同时利用数学家Daubechies推导的滤波器数组,即可构造Daubechies紧支撑小波函数.根据振动信号特性,合理选择小波基,使得与小波基函数相似的能量集中在高幅值的时间尺度上,与小波基函数不相似的能量发散到零幅值的时间尺度平面上,实现小波变换分析.
1.2 小波分解层数自适应性确定
经过限幅处理的原始信号,可以看成微弱振动信息与冲击信号的叠加.在小波域中,随着小波分解层数的增多,分解细节系数的模极大值即微弱振动信号模极大值及稠密程度增大,冲击和噪声信号的模极大值幅值及稠密程度减小,且个数基本保持不变[9].通过模极大值的幅值即可确定小波分解后信号所占比重,从而确定小波分解的自适应层数.
对原始信号进行m(一般m≤6)层分解,获取每层小波细节系数的模极大值序列W2,…,W N-1,如果|Wi|≥|Wi±1|,则i为信号f(t)该层分解的一个模极大值点.在对信号分解过程中,当满足最大模极大值条件式(4)时,则认为原始信号中以微弱振动信号为主,否则原始信号中冲击信号为主.

式中:σ为随机干扰的小波变换系数模的标准差,由随机干扰信号的第2层小波分解的系数值确定,通过它判定局部极大值是否由随机干扰引起,k为优化参数(一般k=2),主要是调节检测微弱振动信号的能力值大小,其值越小,微弱信号被提取出来的能力越强,同时模极大值受随机干扰的影响越大.因此,k×σ项主要消除随机干扰导致的局部极大值的增加,避免微弱振动信号对应的局部极大值点淹没在随机干扰产生的局部极大值中.小波分解层数自适应步骤如图2所示.
1)对原始信号进行一层小波分解;
2)保留一层小波分解的尺度系数,对细节系数重构,得到新的信号,同时判断新信号的模极大值序列是否满足式(4)的模极大值条件,若满足则确定分解层数为1,结束自适应性层数分解,若不满足则对原始信号进一步分解.
3)重复步骤2),直至分解出的细节系数重构信号的模极大值满足式(4).
4)若最后一次分解层数为m,则最终确定分解层数为m-1.
1.3 小波分析滤除冲击信号流程
在掺杂了冲击的振动信号中,冲击信号的幅值一般远大于淹没在冲击信号中的微弱信号幅值,为了快速精准地获取滤除冲击后的微弱信号,先根据实际情况确定是否需要限定冲击信号幅度,并根据实际经验限定冲击信号幅度值,即确定滤波过程中的第1层分解的阈值.限幅后的信号通过自适应层数分解的小波分析后,可获得滤除冲击后的所需信号,其简单信号处理如图3所示.

图2 小波分解层数自适应步骤Fig.2 The step of adaptive layer decomposition of wavelet transform

图3 滤除冲击信号流程图Fig.3 Filtering shock signal flow diagram
2 小波滤除模拟冲击信号
2.1 小波基函数选取
小波基函数Ψj,k(t)具有多样性,不同的小波函数Ψ(t)和相应的尺度函数Φ(t)可以构成不同的小波基,其作用相当于滤波器,采用不同的小波基函数,会产生不同的信号分析结果.
冲击信号具有非明显的高斯分布特性,为了获得较好的数字信号滤除效果,选取的小波基函数需满足有限的支撑长度,较好的频率分辨率.本文根据振动信号特征选取Daubechies小波对冲击信号进行小波分析,由滤波系数可得N分别为2,4,12,20时的尺度函数和小波函数,如图4和图5所示.
由图4和图5可以看出,随着滤波器长度增加,即N值的增加,小波高频系数减小,分解能量越来越集中,尺度函数和小波函数的光滑程度越来越高,频率特性越来越好,即小波重构信号的光滑程度和频率特性提高.但是滤波器长度增加,其支撑长度增加,导致边缘信息和奇异点定位不准确,同时小波变换的计算量增大.在实际应用中综合冲击信号特征以及时域分辨率等要求,在滤除冲击信号的分析中选取DB4小波对信号进行小波分析.DB4小波分解重构对应的滤波系数见表1.

图4 几种DB小波尺度函数图Fig.4 Some DB scaling function

图5 几种DB小波函数图Fig.5 Some DB wavelet function

表1 DB4小波滤波系数Tab.1 DB4wavelet filter coefficients
2.2 模拟冲击信号时域分析
2.2.1 滤除理想冲击信号
选取的模拟信号为理想冲击信号和不同频率正弦信号的叠加f1(t),并在f1(t)信号中加入信号采集系统产生的白噪声n(t),且噪声信号的σ值为0.342 4,f1(t)的表达式为:

式中:ω为角频率.理想冲击信号幅值趋于无穷即A→∞,模拟冲击信号经过经验限幅后其幅值为远小于A.图6(a)为限幅后的f1(t)信号,其中局部放大部分显示f1(t)信号加噪声后效果.f1(t)信号经过分解后,其1~6层的冲击和噪声信号的模极大值序列中的最大 值分 别为9.4,4.6,2.3,1.4,0.73,0.63.其中第4与第5层的模极大值差值为0.67,小于k×σ值0.684 8.因此自适应分解的层数确定为5层.图6(b)为经过小波分析处理得到不同频率正弦的叠加信号.
由图6可以看出,采用本文的自适应小波分析方法可以有效滤除模拟信号中的冲击信号,得到所需微弱振动信息.

图6 分析模拟理想冲击信号Fig.6 Analyze analog ideal shock signal
2.2.2 滤除非理想冲击信号

式中:ω为角频率;A为振幅.图7(a)为f2(t)信号,其中局部放大部分显示f2(t)信号加噪声后效果.f2(t)信号经过分解后,其1-5层的冲击和噪声信号的模极大值序列中的最大值分别为20.0,7.5,6.6,6.1,5.6.其中第3与第4层的模极大值差值为0.5小于k×σ值0.684 8,因此自适应分解的层数确定为4层.图7(b)为经过小波滤除冲击信号后得到的微弱振动信号.
由图7可以看出,对于非理想振动信号,采用本文自适应小波分析方法可以有效滤除冲击,得到淹没在冲击信号中幅值较小且不同频率的正弦叠加信号.
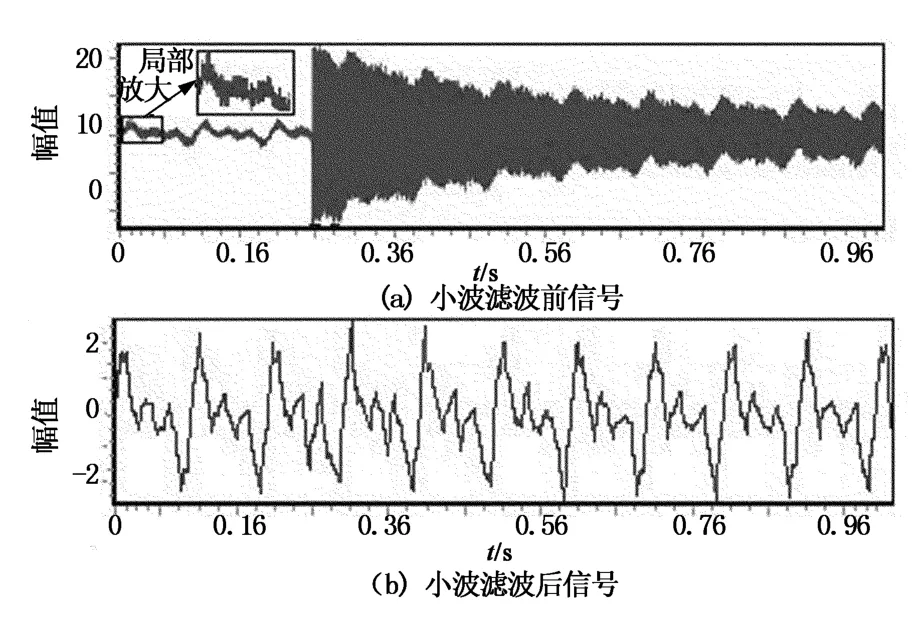
图7 分析模拟非理想冲击信号Fig.7 Analyze analog non-ideal shock signal
3 小波滤除实测冲击信号
3.1 实验系统构成
本实验系统主要由硬件和软件2部分组成,其中硬件部分包括:压电式加速度传感器、高速信号采集卡、电荷放大器、振动信号导向管、力锤和金刚砂.软件部分包括信号采集和处理程序.由力锤和金刚砂产生的振动信号通过安装在振动信号导向管上的压电式加速度传感器送至电荷放大器,将电荷量转换成模拟电压量,然后通过多通道高速采集卡将模拟信号转换为数字信号传输给计算机,最后通过计算机采集与处理程序实现信号的处理与显示,完成对冲击信号的滤除.实验系统如图8所示.
实验系统选用的压电式加速度传感器为PCB-357B03电荷型传感器,灵敏度为10pc/g.采用的高速采集卡主要参数为12位分辨率,连续实时传输速率32 MB/s,传输接口为USB2.0高速屏蔽线.软件设置采样率为80 000 Hz,采样长度8 192个点,系统噪声信号的σ值为0.001 25.

图8 实验系统Fig.8 Experimental system
3.2 实验结果分析
实验信号由2部分组成,模拟油井生产出砂监测过程中对出砂信号的提取[12].第1部分为力锤敲击振动信号导向管后产生的冲击信号,以模拟旋转机械、螺杆泵等对生产管道造成的冲击信号;第2部分为在导向管研磨金刚砂产生的微弱振动信号,以模拟砂砾冲击输油管壁产生的振动信号.
3.2.1 对金刚砂振动信号分析
在导向管研磨金刚砂后产生微弱振动信号,压电式加速度传感器接收到受系统噪声干扰的微弱振动信号,信号通过放大采集后,经过信号采集小波分析处理程序后,得到所需振动信号,如图9所示.

图9 金刚砂振动信号Fig.9 Emery vibration signal
图9(a)为实验系统采集的原始振动信号,振动信号经过分解后,其1~3层的冲击和噪声信号的模极大值序列中的最大值分别为0.006 2,0.005 6,0.005 2.其中第1与第2层的模极大值差值为0.000 6小于k×σ值0.002 5,因此,自适应分解的层数确定为2层.图9(b)为经过小波滤波处理后振动信号,横坐标为振动时间,纵坐标为振动加速度.通过时域波形对比,经过小波滤波后信号幅值基本不变,信号基本保持原有信号特征.
图10为对金刚砂振动信号进行频域分析的结果,通过对比发现频谱特征基本相符.因此利用本文自适应小波分析方法滤除冲击信号时不会对混杂在冲击信号中的重要振动信号造成畸变和干扰.

图10 金刚砂振动信号FFTFig.10 Emery vibration signal FFT
3.2.2 对混有冲击信号的金刚砂振动信号分析
在导向管上研磨金刚砂的同时,使用力锤敲击导向管产生振动信号,经过数据采集处理后如图11所示.
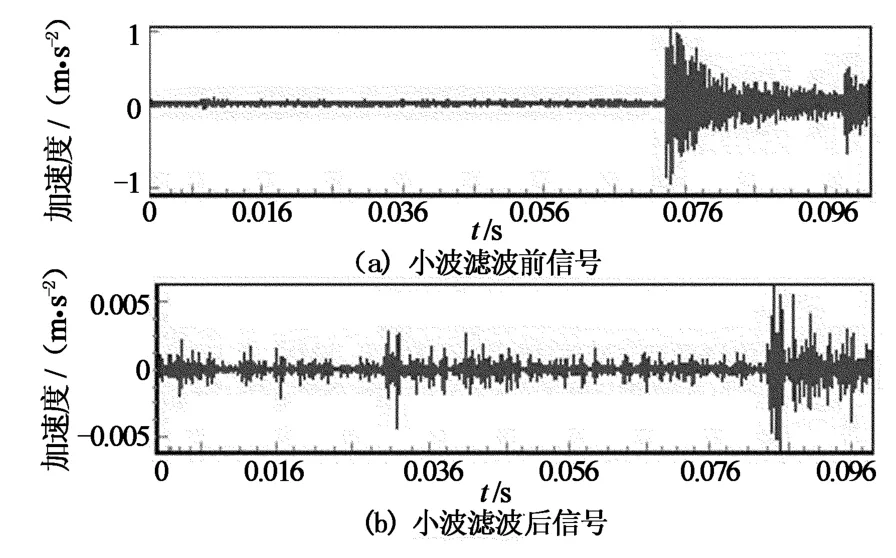
图11 混合振动信号Fig.11 Mixed vibration signal
图11(a)为本实验系统采集的原始振动信号时域波形.振动信号经过分解后,其1~6层的冲击和噪声信号的模极大值序列中的最大值分别为0.073 2,0.052 5,0.027 6,0.018 7,0.010 2,0.008 3.其中第5与第6层的模极大值差值为0.001 9小于k×σ值0.002 5,因此自适应分解的层数确定为6层.图11(b)为经过滤波处理后振动信号时域波形,横坐标为振动时间,纵坐标为振动加速度值.冲击信号加速度最高幅值可达1 m/s2,经过滤波处理后提取的微弱振动信号加速度幅值为0.005m/s2,其幅值与图9(a)中只存在单一金刚砂振动信号加速度幅值一致.从时间角度分析冲击信号持续时间仅为0.024s,而经过滤波分析后信号时间长度为一个完整采样周期时间0.01s.即混杂在冲击信号中的微弱振动信号被提取出来,结果表明一个振动周期内都存在研磨金刚砂产生的振动信号,其中在0.036s和0.096s附近金刚砂振动信号幅值最高.
图12为混合信号频谱分析,从频域角度分析可知,原始混合信号频域范围大概在0~20 000 Hz,经过滤波处理后频域范围集中在12 000~18 000 Hz附近,由文献[13]可知此频段为金刚砂振动频段,因此淹没在冲击信号中的微弱金刚砂振动信号通过本文方法被成功提取出来.

图12 混合信号频谱分析Fig.12 Mixed vibration signal FFT
4 结 论
本文采用自适应层数分解小波分析方法,针对微弱振动淹没在冲击信号中的问题,根据信号特征合理选择小波基,对模拟理想和非理想冲击信号进行自适应层数DB4小波分析,结果表明该方法可以有效滤除冲击信号并提取微弱振动信息.同时,对本实验系统采集的混合振动信号进行自适应DB4小波分析,成功滤除冲击信号.通过模拟计算和实验结果的时频分析可知,自适应小波滤除冲击信号算法正确、结果可靠,自适应层数分解小波分析方法可以滤除冲击提取微弱振动信号,解决工程实际问题.
[1]霍静思,何远明,肖莉平,等.高温后钢管混凝土抗多次冲击力学性能试验研究[J].湖南大学学报:自然科学版,2012,39(9):6-10.
HUO Jing-si,HE Yuan-ming,XIAO Li-ping,etal.Experimental study on the dynamic behavior of concrete-filled steel tube after exposure to high temperatures under multiple impact loadings[J].Journal of Hunan University:Natural Sciences,2012,39(9):6-10.(In Chinese)
[2]郑雪莲,李显生,任园园,等.非满载罐体液体冲击等效机械模型参数确定[J].湖南大学学报:自然科学版,2013,40(6):53-58.
ZHENG Xue-lian,LI Xian-sheng,REN Yuan-yuan,etal.Parameter values of equivalent mechanical model for liquid sloshing in partially-filled tanks[J].Journal of Hunan University:Natural Sciences,2013,40(6):53-58.(In Chinese)
[3]LANGLEY R S.The analysis of impact forces in randomly vibrating elastic systems[J].Journal of Sound and Vibration,2012,331(16):3738-3750.
[4]VIJAYAN K,WOODHOUSE J.Shock amplification,curve veering and the role of damping[J].Journal of Sound and Vibration,2013,333(5):1379-1389.
[5]LI Hui,ZHANG Yu-ping,ZHENG Hai-qi.Application of hermitian wavelet to crack fault detection in gearbox[J].Mechanical Systems and Signal Processing,2013,25(4):1353-1363.
[6]SHARK L K,YU C.Denoising by optimal fuzzy thresholding in wavelet domain[J].Electronics Letters,2000,36(6):581-582.
[7]WANG Zuo-cai,REN Wei-xin,LIU Jing-liang.A synchrosqueezed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction[J].Journal of Sound and Vibration,2013,332(22):6016-6028.
[8]谭继勇,陈雪峰,何正嘉.冲击信号的随机共振自适应检测方法[J].机械工程学报,2010,46(23):61—67.
TAN Ji-yong,CHEN Xue-feng,HE Zheng-jia.Detection method with adaptive stochastic resonance[J].Journal of Mechanical Engineering,2010,46(23):61-67.(In Chinese)
[9]腾军,朱焰煌,周峰,等.自适应分解层数的小波域中值滤波振动信号降噪法[J].振动与冲击,2009,28(12):58-62.
TENG Jun,ZHU Yan-huang,ZHOU Feng,etal.Vibration signal denoising method based on median filter in wavelet domain with self-adaptive level decomposition[J].Journal of Vibration and Shock,2009,28(12):58-62.(In Chinese)
[10]LEE Y S,LEE S K,SHIN K.Piezoceramic cantilever sensor design for weak-impact detection on plates[J].Shock and Vibration,2012,19(5):879-890.
[11]李媛.小波变换及其工程应用[M].北京:北京邮电大学出版社,2010:18-24.
LI Yuan.Wavelet transform and engineering application[M].Beijing:Beijing University of Posts and Telecommunications Publishing House,2010:18-24.(In Chinese)
[12]刘刚,刘彭涛,韩金良,等.油井出砂监测技术现状及发展趋势[J].科技导报,2013,31(25):75-79.
LIU Gang,LIU Peng-tao,HAN Jin-liang,etal.Status and development trends of sand monitoring technology of oil wells[J].Science & Technology Review,2013,31(25):75-79.(In Chinese)
[13]秦敏,刘志国,刘刚,等.基于加速度传感器的高频振动信号检测分析[J].测控技术,2013,32(5):1-4.
QING Min,LIU Zhi-guo,LIU Gang,etal.Research on high frequency vibration signal detection technology based on accelerometer[J].Journal of Measurement and Control Technology,2013,32(5):1-4.(In Chinese)

