基于遗传算法的潮流能水轮机翼型优化设计＊

任毅如，张田田，曾令斌

（1．湖南大学 机械与运载工程学院，湖南 长沙 410082；2．中国长江三峡集团公司，北京 100036；3．广州船舶及海洋工程设计研究院，广东 广州 510250）

随着世界经济的发展，能源消耗越来越多．由于化石能源危机以及传统能源所带来的环境污染和碳排放等问题，使得清洁的可再生能源日益重要．潮流能是一种非常重要的新能源，具有可靠、周期性、分布广泛、且可持续等优点．越来越多的国家已经开展了相关的研究，潮流能将在未来的能源中扮演重要角色．为了利用潮流能，采用水轮机作为主要的能量捕获装置，叶片作为直接承受水动力并将其转化为机械能的部件，对潮流能转化效率有重要影响．因此，叶片是潮流能水轮机设计中的关键部件．

在水平轴潮流能叶片设计中，翼型选择、翼展、以及沿展向分布的弦长、厚度和扭转角度分布均为重要影响参数．此外，翼型前缘粗糙度、平台的升降运动和表面重力波等均会对水动性能产生重要影响［1－2］．为了提高水轮机效率，国内外学者已经开展了相关的研究工作．Wu等人［3］引入Schmitz理论对桨叶进行设计，并充分考虑了空泡问题，能够提高水轮机效率．Battena等人［4］采用试验对动量方法进行了研究，表明该方法具有足够的精度，并采用该方法对叶片进行设计．Reza等人［5］采用响应面方法，以最大化输出功率为目标函数对海洋水平轴水轮机叶片沿展向的厚度和扭转角等进行优化设计．翼型设计是水轮机设计中的关键问题，只有选择合理的翼型，才能最大限度地提高水轮机效率．尽管已经开展了相关的研究，但是大都采用风力机和航空专用翼型，使水轮机无法达到最佳效率．因此，有必要研究适用于水轮机的最佳翼型．

目前，国外的翼型研究与设计主要集中在飞行器和风力机领域，国内学者对风力机翼型也开展了相关研究［6－8］．通过相关学者的研究，已经获得了重要的翼型数据，如专为风力机设计的翼型有SERI翼型、为了减小前缘粗糙敏感度的DU 翼型和CASW1风力机翼型等，它们的共同特点是基于空气动力学原理，大都不是水轮机叶片的理想翼型．以应用最为广泛的NACA 翼型为例，该系列翼型具有较差的失速特性，并且对于前缘粗糙度较为敏感．虽然水轮机和风力机以及飞行器机翼有很多相似之处，但是水轮机叶片的载荷环境有较大的不同．水的密度是空气密度的800多倍，因此水轮机所承受的载荷要大．此外，水轮机在水中运行过程中存在的空化现象可能会对叶片产生较大的破坏．因此相对于风力机叶片，不但需要尽可能避免空化的产生，还要求翼型具有更大的厚度来满足强度要求．目前，仍然缺乏对潮流能水轮机的专用翼型及其分析方法的研究，急需开展相关的研究工作．

目前，在风力机和航空航天领域，已有学者开展了翼型优化设计的研究，Lighthill［9］采用了反设计技术．反设计方法的基本思想是由假定分布在翼型表面的压力系数来构造翼型曲线，通过迭代办法不断修正压力分布来达到指定的设计要求．尽管该方法已被广泛采用，但是在设计过程中无法同时考虑多个设计要求．由于水轮机翼型有多方面的设计要求，必须采用多目标设计方法．Grasso［10］采用基于梯度方法对水轮机翼型在7°攻角下的水动性能进行了优化设计．为了使潮流能水轮机在1～3m／s流速下达到较好的性能，Goundar等人［11］对翼型的高升力、高升阻比、较高的强度以及空泡的出现等问题开展研究．Molland等 人［12］采 用XFOIL 对 二 维 水翼的空泡问题开展研究．尽管在潮流能水轮机优化设计方面已有了一些研究成果，但是在翼型设计方面仍然处于起步阶段，并且国内的相关研究工作基本处于空白，因此急需开展相关研究．

本文以潮流能水轮机叶片翼型为研究对象，建立了翼型优化设计模型，该模型同时考虑了升力系数、阻力系数、升阻比和表面压力系数等因素．为了获得全局最优解，采用遗传算法进行求解，水动性能和压力系数通过XFOIL 数值仿真软件获得，最后采用该方法获得了不同设计目标情况下的翼型，通过对比分析得到了各种翼型的特点，为进一步开展水轮机设计提供依据．

1 水轮机翼型设计要求与优化算法

1．1 水轮机翼型设计要求

由于处于不同的流体介质中，故风力机和水轮机叶片的设计要求有较大的不同．风向和风力具有较大的随机性，风力机叶片的气动弹性等问题较为显著，在风力机设计中，选择较高的设计升力系数能够降低阵风和疲劳载荷，改善风力机的使用寿命．与风力机不同，水轮机的流体环境中的湍流较低，流速较小并且比较稳定，因此疲劳并不是水轮机的显著问题．由于阵风的影响，风力机叶片可能处于失速区域，当攻角到达失速点后，气动效率可能急剧下降．因此，翼型分离点设计显得尤为重要．对于潮流能水轮机，在设计中更希望水动性能不要随着攻角的变化过于剧烈，尤其是在失速区域［13］．在具体的翼型设计中要求分离点随着攻角的增加而缓慢向后缘移动．一般情况下，风力机叶片较为细长，可能产生较大的扭转力矩，所以风力机的力矩系数是一个非常重要的设计参数．而水轮机叶片的展弦比较小，叶片足够刚硬，所以力矩系数在水轮机叶片设计过程中并不是主要因素．

空化现象是水轮机与风力机的最大区别．空泡产生的条件如图1所示，图1中横坐标为弦线位置．由图1可知，当某一流体区域的压力绝对值大于临界空化压力值时就会形成气泡［12］．一般而言，气泡分为惯性（瞬态）空泡或者非惯性空泡．惯性空泡是由一个空气泡在水中迅速破裂，产生了一个冲击波，该类型空泡通常发生在抽水机、螺旋桨和叶轮等机械结构中．非惯性空泡则是由诸如声场等外在某种型式的能量输入迫使流体产生振荡导致的．由惯性空泡的破裂所产生的冲击波可能会对水轮机结构造成破坏，因此，在水轮机叶片翼型设计中应考虑空泡的影响．空泡参数定义如式（1）所示．

式中：pv为空泡压力，主要依赖于水的温度；p0为局部压力；q为动压．

压力系数定义为：

根据翼型表面的压力分布可以判断是否产生空泡，当pL与pv相等或者最小的负压系数Cp与空泡系数相等时就会产生空泡现象．

图1 空泡产生的条件Fig．1 Condition for cavitation

水轮机沿展向由不同的翼型组成，靠近桨叶外侧部位，要求翼型具有较大的升力系数和升阻比以及较小的阻力系数，使得采用较小的弦长就可以达到指定的水动力载荷．从水动力学设计的角度，翼尖区域的升阻比是最为重要的参数，由于水轮机所受到的载荷较大，为了满足结构设计的要求，一般采用较厚的翼型．由于靠近翼根部位承受了极大的载荷，为了结构布置的需要，对翼型厚度有特别要求，但此时又会牺牲较大的水动性能．在不同设计要求的情况下，翼型会出现较大的不同，如何根据水轮机的要求来设计特定的翼型成为了需要深入研究的问题．

1．2 遗传算法

优化算法可以分为基于梯度和非梯度两类方法，基于梯度的优化方法难以得到全局最优解，并且对翼型设计可能会存在收敛速度慢等问题；诸如遗传算法的非梯度方法具有全局寻优性能，因此，本文采用遗传算法作为优化算法．

遗传算法是以自然选择和遗传理论为基础，将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法．该算法由一组初始解（初始种群）组成，每一个解采用二进制编码如式（3）所示，所有n个设计变量编码成一个二进制数并顺序排列，选择一个适应度函数，并对每一个解的适应度进行评估，淘汰适应度差的解，通过对编码后的二进制数进行变异、杂交等操作获得新解．从而形成了新的种群，重复上述过程，经过若干代的求解能够接近甚至获得全局最优解．

相对于传统优化方法，遗传算法具有可行解表示广泛性、群体搜索性、随机搜索性和全局性等优点，在各类优化方法中被广泛采用［14－15］．

2 翼型优化模型

2．1 翼型参数化方法

设计变量的选择对优化结果非常重要，为了能够准确描述翼型，又不过多牺牲几何信息，拟合曲线的选取至关重要，多项式样条曲线能够显著减少设计变量的个数［16］．本文采用了三次样条曲线，为了尽可能扩大搜索空间，在翼型曲线上选择若干个点，采用每一个点的横坐标和纵坐标作为设计变量，通过翼型曲线上的点（xi，yi）i＝1，…，k以及前缘和后缘的切线斜率（t0，t1）来拟合翼型曲线．最终翼型设计变量X如式（4）所示．

2．2 翼型评估方法

一般而言，翼型水动性能和压力分布可由计算流体力学（CFD）软件得到．对于流速较低的水动力学问题计算精度较高，但是由于翼型优化需要大量评估目标函数，计算量极大，因此该方法并不适合．XFOIL是一款由Drela开发的能够准确评估翼型气动力的数值软件，该软件基于面元法和粘性边界层等模型，与CFD 计算结果接近，能够快速准确地评估翼型，是进行翼型优化设计的理想方法［17］．

2．3 优化模型

潮流能水轮机翼型优化以升力系数、阻力系数、升阻比和压力系数的函数作为目标函数，XFOIL 作为评估工具，将翼型参数化之后，建立如下所示的翼型优化模型．

目标函数为：

约束条件为：

式中：CL，CL／CD，CD和Cpmax分别为升力系数，升阻比，阻力系数和压力系数最大值；分别为第i个设计变量及其上下界，此处的设计变量为翼型上节点坐标等．目标函数f（X）可以是水动性能和压力系数的任意组合形式，在实际翼型设计中可以根据需要灵活选择．

依赖于翼型变量的目标函数，同时满足等式和不等式约束条件，通过求解优化模型可以得到满足设计要求的翼型．

3 水轮机叶片翼型优化设计

对于潮流能水轮机，叶片沿展向的不同位置有不同的设计要求，靠近翼尖位置，具有较高升阻比的薄翼型是较优的选择，在一个较宽的攻角范围内，必须具有较高的升力系数和升阻比，阻力系数应当尽可能小．由于根部承受较大的载荷，为了保证桨叶具有足够的结构刚度和强度，要求根部翼型具有较大的厚度．此外，为了避免空化现象，可能需要选择较厚的翼型．为了验证本文方法，并探讨翼型特性，采用Reynold数为106，目标函数是攻角为3°情况的升力系数、阻力系数、升阻比和压力系数，获得不同设计要求下的翼型，并对比各个翼型的水动性能和压力分布特性．

基于本文所提出的优化模型和求解方法，对几种不同设计要求进行求解，最终得到每种情况下的翼型曲线如图2所示．由图2可知，当最小化阻力系数和最大化升力系数时，翼型曲线较为接近；当最大化升阻比时，最大厚度位于距翼型前缘35%处，最大厚度为弦长的8．8%；在最小化阻力系数情况下，最大厚度距前缘35%，最大厚度为弦长的8．3%．对于水轮机而言，由于较大的升力部分转化为垂直于水轮机平面的推力，而转化为水轮机轴向力的部分较小．不同于升力系数，阻力系数的降低能够显著提高水动性能．区别于前两种翼型，最大化升力系数和最小化最小压力系数所获得的翼型有较大的不同，在最大化升力系数情况下，翼型前部较厚，到后缘处翼型厚度减小，最大厚度位于距翼型前缘39%处，最大厚度为弦长的11．4%；而对于最小化最小负压系数，最大厚度位于距翼型前缘52%处，最大厚度为弦长的8．8%．

图2 不同目标函数情况下的翼型对比Fig．2 Hydrofoil for different objective function

图3 不同翼型的升力系数随攻角的变化Fig．3 Lift coefficient vs．attact angles for different hydrofoil

图4 不同翼型的阻力系数随攻角的变化Fig．4 Drag coefficient vs．attact angles for different hydrofoil

不同设计目标函数情况下的升力系数、阻力系数和升阻比如图3－图5所示．与翼型数据结果类似，最小化阻力系数和最大化升阻比所得到的两种翼型具有非常接近的水动性能．以负压系数作为目标函数情况下，升力系数大大小于其他3种情况，阻力系数则与最小化阻力系数情况接近．尽管最大化升力系数具有较大的升力系数，但是阻力系数明显大于其他翼型的阻力系数，并且该翼型虽然在3°攻角情况下具有最大的升力系数，但是随着攻角的增加，最大化升阻比和最小化阻力系数时的翼型具有更大升力系数．因此在进行翼型设计时，不能只考虑一种攻角下的水动性能，而要进行综合考虑．

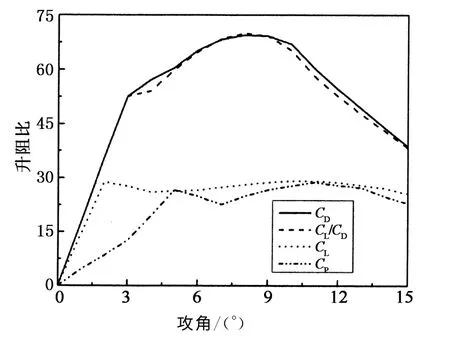
图5 不同翼型的升阻比随攻角的变化Fig．5 Lift－drag ratio vs．attact angles for different hydrofoil

4种不同翼型在3°攻角情况下的表面压力系数如图6所示．由图6可知，最小化压力系数时的压力分布最为均匀，最小值为－0．5，可见最小化压力系数可以大大改善翼型表面的压力分布，进而避免空化现象的产生．最小化阻力系数和最大化升阻比情况下的翼型，最小压力系数为－1．1，两者较为接近．最大化升力系数情况下的最小压力系数峰值最小，达到了－1．5，也越容易产生空化现象．

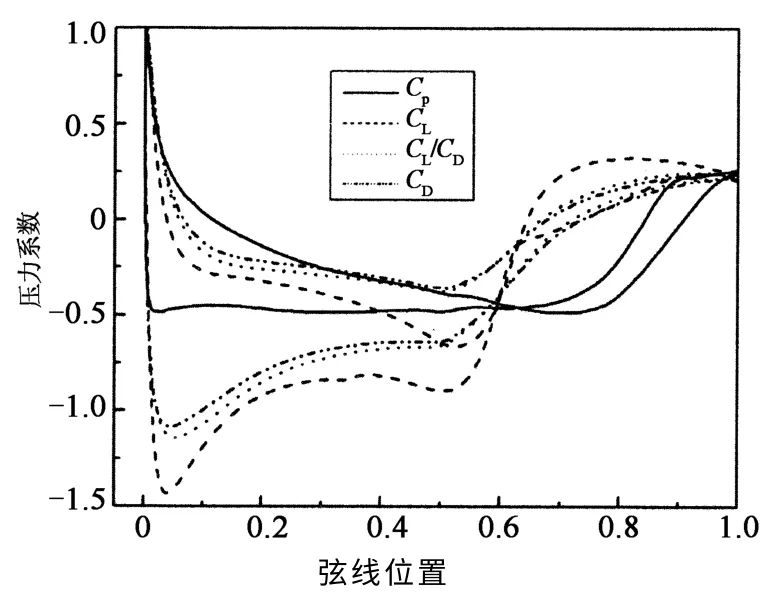
图6 不同翼型的3°攻角下的压力分布Fig．6 Pressure distributions of 3°attact angle

不同攻角下的翼型表面压力系数对比如图7－图10所示．由图可知，不同攻角下的同一翼型压力系数分布规律较为一致．随着攻角的增加，最小压力系数也随着减小，而且压力分布会更加不均匀．尽管最小化压力系数情况下，翼型在3°攻角时具有最佳的压力分布特性，但是随着攻角的增加，最小压力系数急剧增加，显然对避免空化现象不利，因此，需要综合考虑多个攻角下的压力分布系数．

图7 最大升力系数翼型时不同攻角的压力分布Fig．7 Pressure distributions for maximum lift coefficient

图8 最大升阻比翼型时不同攻角的压力分布Fig．8 Pressure distributions for maximum lift－drag ratio

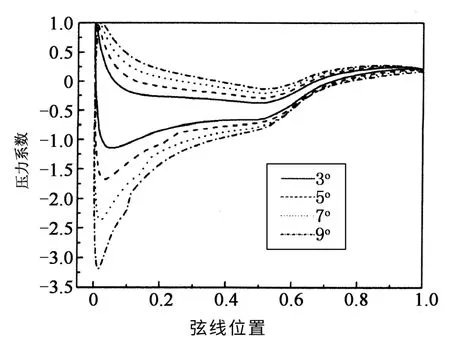
图9 最小化阻力系数翼型时不同攻角的压力分布Fig．9 Pressure distributions for minimized drag coefficient

图10 最小化压力系数翼型时不同攻角的压力分布Fig．10 Pressure distributions for minimized pressure coefficient

4 结 论

本文针对潮流能水轮机叶片翼型，提出了一种优化设计方法．该方法采用了具有全局寻优特性的遗传算法，选取的曲线拟合方法能够准确地描述翼型曲线，通过该模型获得的翼型不仅能够提高水动力性能，还能改善翼型的空化问题．在最大化升力系数情况下，翼型具有较小的阻力系数，以压力系数为目标函数能够显著改善压力系数分布特性．为了改善水轮机性能，需要考虑多个攻角进行综合设计．通过该方法能够显著改善潮流能水轮机翼型的水动性能和压力分布特性．

［1］ZHANG L，WANG S Q，SHENG Q H．The effects of surge motion of the floating platform on hydrodynamics performance of horizontal－axis tidal current turbine［J］．Renewable Energy，2015，74：796－802．

［2］LUST E E，LUZNIK L，FLACK K A，etal．The influence of surface gravity waves on marine current turbine performance［J］．International Journal of Marine Energy，2013，3／4：27－40．

［3］WU B G，ZHANG X M，CHEN J M，etal．Design of highefficient and universally applicable blades of tidal stream turbine［J］．Energy，2013，60：187－194．

［4］BATTENA W M J，BAHAJ A S，MOLLAND A F，etal．Experimentally validated numerical method for the hydrodynamic design of horizontal axis tidal turbines［J］．Ocean Engineering，2007，34：1013－1020．

［5］REZA C，MARTIN O，RALF B．Blades optimization for an ocean current horizontal axis turbine using response surface methodology［C］／／OCEANS．Spain：IEEE，2011．

［6］白井艳，杨科，黄宸武，等．风力机专用翼型的反设计［J］．工程热物理学报，2012，33（11）：1884－1888．

BAI Jing－yan，YANG Ke，HUANG Chen－wu，etal．The inverse design of wind turbine airfoil［J］．Journal of Engineering Thermophysics，2012，33（11）：1884－1888．（In Chinese）

［7］王林，刘雄伟．风力发电机叶片翼型气动性能分析与数值模拟［J］．太阳能学报，2012，33（5）：711－716．

WANG Lin，LIU Xiong－wei．Numerical simulation and analysis on aerodynamic performance of wind turbine blade［J］．Acta Energiae Solaris Sinca，2012，33（5）：711－716．（In Chinese）

［8］王龙，宋文萍，许建华．基于Pareto 遗传算法的风力机翼型多点优化设计［J］．太阳能学报，2013，34（10）：1685－1689．

WANG Long，SONG Wen－ping，XU Jian－hua．Multipoint optimization wind turbine airfoils based on Pareto genetic algorithm［J］．Acta Energiae Solaris Sinca，2013，34（10）：1685－1689．（In Chinese）

［9］LIGHTHILL M J．A new method of two－dimensional aerodynamic design［R］．London：Aeronautical Research Council，Reports and Memoranda，1945．

［10］GRASSO F．Design and optimization of tidal turbine airfoil［J］．Journal of Aircraft，2012，49（2）：636－643．

［11］GOUNDAR J N，AHMED M R．Design of a horizontal axis tidal current turbine［J］．Applied Energy，2013，111：161－174．

［12］MOLLAND A F，BAHAJ A S，CHAPLIN J R，etal．Measurements and predictions of forces，pressures and cavitation on 2－D sections suitable for marine current turbines［J］．Journal of Engineering for the Maritime Environment，2004，218（2）：127－138．

［13］AHMED M R．Blade sections for wind turbine and tidal cureent turbine applications－current status and future challenges［J］．International Journal of Energy Research，2012，36：829－844．

［14］官凤娇，韩旭，周长江，等．基于微型多目标遗传算法的布料机臂架结构优化［J］．湖南大学学报：自然科学版，2008，35（11）：26－31．

GUAN Feng－jiao，HAN Xu，ZHOU Chang－jiang，etal．Design optimization of the telescopic boom of concrete distribution machine based on micro multi－objective genetic algorithm［J］．Journal of Hunan University：Natural Sciences，2008，35（11）：26－31．（In Chinese）

［15］邓乾旺，高礼坤，罗正平，等．基于多目标遗传算法的起重机吊装路径规划［J］．湖南大学学报：自然科学版，2014，41（1）：63－69．

DENG Qian－wang，GAO Li－kun，LUO Zheng－ping，etal．Lifting path planning of crane based on multi－objective genetic algorithm［J］．Journal of Hunan University：Natural Sciences，2014，41（1）：63－69．（In Chinese）

［16］SAMAREH J A．Survey of shape parameterization techniques for high－fidelity multidisciplinary shape optimization［J］．AIAA Journal，2001，39（5）：877－884．

［17］DRELA M．XFOIL：An analysis and design system for low Reynolds number airfoils［J］．Low Reynolds Number Aerodynamics，1989，54：1－12．