基于三角区域有理函数的图像自适应插值

宁 阳， 张云峰， 高珊珊， 迟 静， 张彩明

（1. 山东财经大学计算机科学与技术学院，山东 济南 250014；2. 山东省数字媒体重点实验室，山东 济南 250061；3. 山东大学计算机科学与技术学院，山东 济南 250100）

基于三角区域有理函数的图像自适应插值

宁 阳1,2， 张云峰1,2， 高珊珊1,2， 迟 静1,2， 张彩明1,3

（1. 山东财经大学计算机科学与技术学院，山东 济南 250014；2. 山东省数字媒体重点实验室，山东 济南 250061；3. 山东大学计算机科学与技术学院，山东 济南 250100）

基于有理函数模型提出了一种新的图像插值算法。此类有理函数基于三角区域构造并且具有简洁且灵活的表达式，同时含有一个可调节参数，在不改变插值曲面输入数据的前提下，可以通过调整参数来微调曲面弯曲程度从而达到更加理想的插值效果。首先将图像区域进行三角剖分，将有理函数模型定义域转化到其特殊域（等腰直角三角形域），通过区域变换使插值曲面达到更好的连续性和光滑性，有效提升了插值精度；然后利用一种基于边缘走向的权值确定方法分别确定各个三角域的权值；最后通过等值线分析将图像划分为不同区域，在平滑区域上随机选择或者固定参数进行插值即可，在非平滑区域上则进行参数的最优化选取，使当前的插值曲面块达到最优，进一步提升了插值精度。本文算法在边缘区域和纹理信息保持方面相对于传统插值算法具有一定的优势，有效地消除了常见的振铃、走样等现象，并且具有良好的视觉效果。

有理函数插值；等值线分析；图像自适应；参数最优化

图像插值技术是从低分辨率图像(low resolution, LR)通过某种算法恢复其高分辨图像(high resolution, HR)的一类图像处理技术。通过已知像素和未知像素之间的关联恢复未知像素的研究一直都在进行，对平滑区域的处理技术已经日渐成熟，传统的插值方法：如最近邻、双线性，双三次、三次样条插值等[1-2]足以胜任。相对于图像的平滑区域，人的视觉系统对边缘区域更加敏感，所以如何比较好地恢复真实边缘就显得至关重要。目前比较好的插值算法能够在保持锐利边缘的同时，还能够基本杜绝振铃，走样等现象的出现。

为了获得更好地视觉效果同时解决上述的问题，不断有学者提出新的插值算法，其中较流行的做法是把图像自适应划分为不同区域，并分别用不同的方法进行处理，其好处是在提高算法效率的同时并不会损失图像处理质量。文献[3]提出一种基于小波的图像插值处理方法，可分离的小波仅仅能获得有限的方向信息，这使图像的边缘信息不能得到很好地保持。文献[4]提出一种基于边缘指导的插值算法(new edge-directed interpolation, NEDI)，基本思想是首先通过低分辨率图像估计局部协方差系数，然后根据几何对偶性，用低分辨率图像的协方差估计高分辨率图像的协方差。此算法可以将边缘处理的很好，但是对细节的保持稍有欠缺。文献[5]提出了一种基于多方向滤波和数据融合的插值算法(edge-guided image interpolation via directional filtering and data fusion, DFDF)，此算法是一种非线性插值技术，对于要插值的像素而言，定义了两组垂直方向的观测集，每一个集合都生成一个被插像素的估计值（通过传统的线性插值生成）。这些多方向的估计值，通过为丢失像素增加一个噪声项进行建模，最终通过线性最小均方误差估计被融合为一个更加鲁棒的估计，这个估计用到了两组观测值的统计资料。由于线性均方误差估计要用到的一些条件概率，现实生活中很难得出和计算复杂度比较高的问题，作者提出了一种比较简化的方法，用均方误差估计代替线性均方误差估计，经过实验发现很好地保持了边缘的锐度并且消除了振铃现象。文献[6]提出了一种基于自回归模型和软决策估计的图像插值算法(image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation, SAI)，可通过软决策插值技术，一次估计一组丢失的像素而不是只估计一个像素。这个新技术可通过二维分段的自回归模型适应于不同的场景结构。通过在低分辨率像素矩阵滑动一个窗口来估计这个自回归模型的参数。此算法能够在低分辨像素之间，低分辨像素和高分辨率像素之间产生一种反馈机制，有效地提高了算法的鲁棒性，此算法效果要优于上述算法，更好地保持了边缘和细节，但是在处理某些图像时会发生比较严重的走样。

本文算法充分利用了有理函数的优点和性质，在插值数据不改变的前提下可以通过修改参数α来达到最理想的插值曲面。首先利用等值线把图像自适应地分解为平滑区域和非平滑区域。在图像的平滑区域，经过实验发现参数α对插值结果影响不大，可以随机取值；在图像的非平滑区域，通过三角区域的已知HR像素的反馈，自适应地计算出最优参数α，有效地提高插值精度。由于本文算法将边缘方向信息进行融合，所以比较好地保持了边缘，细节保持方面也相对优于上述算法，而且不会出现走样问题。实验结果表明，本文算法能够取得较好的主观和客观效果。

1 三角域上的有理插值函数模型

插值模型决定了图像的插值质量，含有参数的有理插值函数要比不含参数的更精确，同时基于三角域的有理插值函数插值模型相对于其他模型显得更加灵活。在本节，将重点介绍基于三角域上的有理插值函数模型和其所具有的性质。

1.1 双变量单参数有理插值函数

文献[7-14]构造了多种有理样条插值模型，其均具有非常简洁的表达式，且有不错的插值效果。

令｛（xi,yi,fi,di）,i=1,2,…,n｝作为给定的离散数据，这些数据分布在平行线： e1,e2,…,em上，

对于一个三角区域T1=ΔV1V2V3，有顶点集｛Vi=（xi,yi）,i =1,2,3｝，并且y1=y2，让γ11=∠V3V1V2是线V3V1和V1V2的夹角，γ12是线V2V3和 V1V2的延长线的夹角。

令h=x2-x1,l=y3-y1。对于在线V1V2上的任意一点Q，让β=∠V3QV2作为线V3Q和QV2的夹角，因此，V1Q=x3-x1-lcotβ，并且对于在线V3Q上的任意点让并且一个有理三次函数在区间［x1x2］,上被定义为下式：

其中：

令α＞0。显然，在［x1,x2］上的插值函数p（x）对于给定数据（xi,fi,di）,i=1,2和参数α是唯一的，且满足下式：

用x方向的插值函数p（x），可以在 T1域上如下定义这个双变量有理插值函数P（x, y）：

这个被叫做位于三角区域1T上的双变量有理插值公式。

所以，这个插值函数满足：

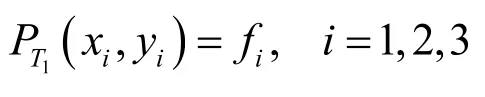
对于 T2,T3和 T4则可以利用对称性进行求解，这里不再做过多的叙述，因为后面算法中的数据都已经被转换到 T1域进行运算，并且这个有理函数插值模型对于不同的域（T1,T2,T3,T4）之间是C0连续的，所以如果将数据集中转换到一个域(如 T1)进行运算，则有效避免了函数连续性低的缺点。

1.2 插值函数的性质

为了方便应用到图像插值上，上述公式可以改写成如下形式：

其中：

对于给定的插值数据｛（xi,yi,fi,dj）,i=1,2,3; j=1,2｝，让PT1（x,y）如上面公式所述在三角区域T1定义为插值函数，无论参数α怎么取值，在 T1的取值都满足：

其中：

由于式(2)的值会随着参数的调整而不断地改变，但是上式对其取值给定了一个约束，无论参数怎样变化，其取值都会在一个范围内，也就是定界。如果在插值过程中，像素值出现了剧烈波动，例如不在上述不等式约束的界内，则可以通过相关的技术手段予以调整，使其满足上式的约束条件。

2 基于三角区域的有理插值算法和优化

2.1 三角区域转换和插值

根据1.1节介绍的有理函数模型可知，此有理函数为分段C0连续，本文通过对三角形的各个顶点进行重新排列的方式，将每个三角形转化为同一个分段，从而避免了各分段之间C0连续的弊端，有效提升了插值效果。如图 1所示，观察图中的两个等腰直角三角形，图中只给出了右边三角形经过调整后顶点的排列（将图旋转 180°后观察到的三角形顶点排列即为约定的规则排列，其他三角形按照此规则进行顶点排列）。按照从左到右，从上到下的顺序来看左边的三角形，其 3个黑色的顶点的规则排序即为 V3,V2,V1，这样就可顺利的将左右两个等腰直角三角形转化到了同一个分段，既方便应用又有效避免了C0连续的缺点，具体如何实现，本文将做进一步展开。

图1 插值算法

首先把一个16邻域像素矩阵抽象成上下左右4个方向，现在只讨论上方向，其他3个方向按照同样的方式对待。如图1所示的A值并非这个位置上的最终像素值，而是为了辅助计算丢失的像素，其他方向的同样位置上同理，这样丢失像素最终可以由8个像素值（4个精确的LR像素，4个辅助像素）通过加权平均计算。由于每一个三角形有 3个顶点，正好作为有理函数的输入点，通过1.1节介绍的有理插值模型发现V3的比重是随着要求点的坐标位置而确定的，一旦要求点的坐标给定，则V3这个点对三角区域所求点像素的贡献就确定了（V3这个点的基函数不含参数），但是考虑到边的方向因素，沿着边的方向像素值贡献应该要大于非沿着边的方向像素值，所以还需要估计每个三角形的局部方差来对3V的贡献进行重新调整。先把上方向的两个三角形根据左右进行编号（左1右2），分别对两个三角形包含的像素求局部方差，记为1Var和2Var，然后按照式(3)对左右两个三角形分别确定权值，加权平均后得到辅助像素值A，其他3个方向同理。

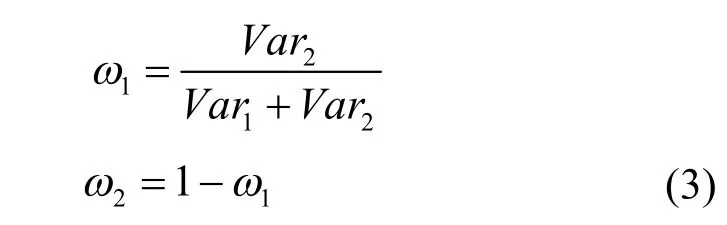
对于丢失像素而言，现在有4个精确的LR像素和4个辅助像素，其中4个LR像素由于是精确值，所以其对丢失像素的贡献值要大于 4个辅助像素，通过实验发现，可以分配2/3比重的权值给4个精确的LR像素，剩下的1/3分配给4个辅助像素。考虑到边的走向的因素，按照 45°和 135°方向把4个LR像素划分为两组，然后分别求局部方差，之后利用式(3)对其分配子权值。最后通过对 8个像素加权平均，求出丢失像素，其他的丢失像素可以通过将像素矩阵旋转 45°后用上述同样的算法进行求解。

通过对三角区域有理插值模型的进一步分析可知，由于在确定所求点坐标后3V对丢失像素值的贡献就是确定的（3V的基函数并不包含任何参数），1V和2V都包含一个可调控参数，同时两个偏导数也在1V、2V连线的方向上，所以得出一个结论：影响插值结果的重点方向是1V、2V连线的方向。对于图 1上方向的两个三角形，可以将求所有点的局部方差简化为求两个三角形1V、2V连线方向的局部方差，而这两个方向又是垂直的，然后利用式(3)，求出权值进行插值即可。

2.2 图像自适应分解

对图像来说，平滑区域结构比较简单，而边缘区域结构比较复杂，保存了图像的大部分信息，是图像中最重要的区域，因此插值算法要适应边缘区域复杂的像素结构。为了权衡插值速度和插值质量，可以通过绘制等值线将图像自适应分解为平滑区域和边缘区域，找到局部区域是否存在边缘或者纹理，甚至可以找到边缘的走向。等值线是制图对象某一数量指标值相等的各点连成的平滑曲线，其绘制方法具体如下：对要处理区域所有涉及像素取平均值，然后用丢失像素四邻域的LR像素分别与做差，会得到4个值。如果这4个值同时为正或者同时为负，那么可以认为其处于平滑区域；否则就认为其处于像素波动比较大的边缘或者纹理区域。同时可以根据符号的正、负和丢失像素的正、负大致地判断出边缘的走向，这个走向对像素权值的确定也同样重要。

相对于图像的边缘或者纹理区域，平滑区域占据了图像的绝大部分，所以如果能够自适应的把图像划分为两部分来进行处理，则会极大地降低算法的计算复杂度，提高算法的执行效率。通过绘制等值线，丢失像素的四邻域如果符号同时为正或者同时为负，则认为是平滑区域，否则认为是非平滑区域。对于平滑区域只需按照传统的插值方法或者简化的算法进行处理即可，因为对于图像的平滑区域而言，传统的线性插值算法足以胜任，而对于非平滑区域，则要按照本文算法进行处理。

2.3 参数的最优化

在将图像自适应分解为平滑区域和非平滑区域以后，着重分析如何计算非平滑区域的最优化参数，而对于平滑区域，经过试验发现参数如何选取对最终插值效果影响不大。在利用1.2节提到的式(2)进行丢失像素求解时，平滑区域由于像素变化比较平缓，经过实验发现，参数取值对结果影响不大，所以在平滑区域可以随机取参数；而在于图像像素变化比较剧烈的边缘或者纹理区域，如果能够选择最优化参数，则可以降低误差，有效地提高图像插值质量。

式(2)是一个包含双变量单参数的有理函数插值模型，求这个最优化参数α，让它能够最适应当前这一小块插值曲面。通过观察图 1和图 2 (将图1中的右边的三角形旋转180°)，可发现每一个三角区域除了V1,V2,V33个精确点外，还有V4,V5,V63个精确点，所以可以利用 V4,V5,V6这3个值反推出3个参数α1,α2,α3，然后取平均后得到值，可以认为这个就是这个小三角区域的最精确的参数值α，之后将这个α和 V1,V2,V33个精确点带入式(2)，最后再按照本文算法进行求解即可。

图2 参数最优化

3 实验结果

3.1 实验设置

经过同提出的几种经典插值算法的多次比较且做了大量的实验，本文选择了 Dollar, Barbara, Lighthouse, Milkdrop, Lake 5张图片作为测试图片，自然图像的多样性使得同一种算法在不同图像上可能有不同的效果，这要求在实验中选用具有代表性的，包含多种情形的测试图像。如图 3所示，这几张图片有的比较复杂，包括很多纹理区域和渐变结构(Barbara, Lighthouse)，有的平滑区域比较多，过渡比较自然(Milkdrop)，这样可以比较全面的考验本文算法的执行能力，有效地测试其鲁棒性。

图3 标准测试图像

3.2 插值效果和插值速度的比较

就插值效果来看，针对表 1中的两种经典算法NEDI和SAI进行峰值信噪比(peak signal noise ratio, PSNR)的数值比较，PSNR是一种对图像的客观评测数据。图4、图5是对图3红线标示区域进行局部放大后的对比图，图4可以看到NEDI算法，SAI算法在栅栏处有明显的走样现象；图5在围巾部位NEDI算法、SAI算法同样有走样现象，而且还产生了一些伪边界，而本文算法则比较好地恢复了图像的边界走向。图 6～8分别为每幅完整图片对应算法的重建效果图。本文算法在主观和客观效果上优于NEDI算法，虽然在PSNR数值上略差于SAI算法，但是在平均数值上要优于SAI算法，在现实的应用中，平均数据值通常比单个测试的数据更有意义。另还需要进一步努力，继续完善本文算法。因为客观评测仅仅是数值上的比较，并不能很好的反应图片的插值效果，所以还需要进一步对其进行主观评测。

就插值速度来看，NEDI算法首先通过LR图像估计局部协方差系数，然后根据几何对偶性，用LR图像的协方差估计HR图像的协方差，而且利用局部方差是否达到一个阈值来区分像素位于平滑区域还是非平滑区域。通过实验发现，NEDI算法这样做虽然可以取得不错的效果，但是代价也是比较大的。因为协方差和局部方差的计算需要进行大量的乘法计算，所以速度比较慢，考虑此因素，本文决定采用等值线绘制的方法来区分像素所处的区域。由于等值线的绘制只需要一次除法运算（用来求均值），其余的也都是简单的加减运算，所以本文算法的时间复杂度有比较大的提升。同时等值线还会绘制出区域内的伪边界方向，这也为像素的权值估算提供了重要依据。同理，SAI算法也是用局部方差进行像素所处区域的区分，同时由于它采用了一种自回归模型，要进行一定程度的迭代操作，所以相对于本文算法来说，时间复杂度也比较高。总之，由于有理函数的特点就是计算速度快，所以本文算法在时间上占优势。

表1 不同算法的峰值信噪比值比较

图4 Lighthouse的局部比较

图5 Barbara的局部比较

图6 Dollar图像比较

图7 Milkdrop图像比较

图8 Lake图像比较

4 结 论

本文提出一种基于三角区域有理函数的图像自适应插值算法，通过三角剖分把图像划分为不同的区域，然后对每个三角区域的顶点重新排序，自动地将所有不同的三角域转换到相同的区域进行插值，使插值曲面保持更好地连续性和光滑性。权值更好地考虑到了方向的信息。通过绘制等值线能够比较直观地分解出平滑区域和非平滑区域，在不同的区域用不同的算法进行插值，可以更好地权衡算法的效率和质量。本文算法有效地消除了常见的振铃、走样等现象，同时具有较好的主观和客观效果，但是由于三角域比较灵活造成权值确定的过程很难把所有相关因素考虑在内的原因，本文算法的边缘还是存在一些锯齿现象，如何更好地解决这个问题将是下一步研究的重点之一。

[1] Keys R G. Cubic convolution interpolation for digital image processing [J]. IEEE Transactions on Acoustics, Speech and Signal and Processing, 1981, 29(6): 1153-1160.

[2] Hou H S, Andrew H C. Cubic splines for image interpolation and digital filtering [J]. IEEE Transactions Acoustics, Speech and Signal and Processing, 1978, 26(6): 508-517.

[3] 蔡 念, 张海员, 张 楠, 等. 基于小波的改进加权抛物线插值的图像超分辨率算法[J]. 图学学报, 2012, 33(1): 50-56.

[4] Li Xin, Orchard M T. New edge-directed interpolation [J]. IEEE Transactions on Image Processing, 2001, 10(10): 1521-1527.

[5] Zhang Lei, Wu Xiaolin. An edge-guided image interpolation algorithm via directional filtering and data fusion [J]. IEEE Transactions on Image Processing, 2006, 15(8): 2226-2238.

[6] Zhang Xiangjun, Wu Xiaolin. Image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation [J]. IEEE Transactions on Image Processing, 2008, 17(6): 887-896.

[7] 刘 植, 张 莉, 时 军, 等. 基于函数值的线性有理插值样条[J]. 工程图学学报, 2009, 30(6): 86-90.

[8] Zhang Caiming, Zhang Xin, Li Xuemei, et al. Cubic surface fitting to image with edges as constraints [C]//IEEE. the International Conference on Image Processing (ICIP). Melbourne, Australia, 2013: 1046-1050.

[9] Hung K W, Siu Wanchi. Robust soft-decision interpolation using weighted least squares [J]. IEEE Transactions on Image Processing, 2012, 21(3): 1061-1069.

[10] Zhang Yunfeng, Bao Fangxun, Zhang Caiming, et al. Local shape control of a bivariate rational interpolating surface with mixing conditions [C]//IEEE. The International Symposium on Voronoi Diagrams in Science and Engineering (ISVD), Qingdao, China, 2011: 200-205.

[11] Duan Qi, Zhang Huanling, Zhang Yunfeng. Bounded property and point control of a bivariate rational interpolating surface [J]. Computers and Mathematics with Applications, 2006, 52: 975-984.

[12] Duan Qi, Zhang Yunfeng, Twizell E H. A bivariate rational interpolation and the properties [J]. Applied Mathematics and Computation, 2006, 179: 190-199.

[13] Zhang Yunfeng, Duan Qi, Twizell E H. Convexity control of a bivariate rational interpolating spline surfaces [J]. Computers and Graphics, 2007, 31(5): 679-687.

[14] Duan Qi, Bao Fangxun, Zhang Yunfeng. Shape control of a bivariate interpolating spline surface [J]. International Journal of Computer Mathematics, 2008, 85(5): 813-825.

Adaptive Weighted Interpolation Based on Rational Function over Triangular Domain

Ning Yang1,2, Zhang Yunfeng1,2, Gao Shanshan1,2, Chi Jing1,2, Zhang Caiming1,3

(1. Department of Computer Science and Technology, Shandong University of Finance and Economics, Jinan Shandong 250014, China; 2. Digital Media Technology Key Laboratory of Shandong Province, Jinan Shandong 250061, China; 3. Department of Computer Science and Technology, Shandong University, Jinan Shandong 250100, China)

This paper proposed a novel image interpolation algorithm based on the rational function model. The interpolation function is carried out by a simple and explicit mathematical representation through a parameter and the shape of the interpolation surface can be modified by using the parameter for the unchanged interpolation data. Firstly, we change the domain of definition of the interpolation function into a special domain (the domain of the isosceles right triangle), then the interpolation surface will be smoother and the interpolation precision will be improved effectively. Secondly, we have given more consideration to the directional information of the image. Finally, the image is divided into smooth area and non-smooth area by drawing contour lines. Then we select a random or a fixed parameter in smooth area and choose the optimal parameter in non-smooth area. The experimental results show that the algorithms proposed by this paper achieve comparatively good effects and the common interpolation artifacts (ringing, aliasing, etc) are greatly reduced.

rational function interpolation; contour lines; adaptive; parameter optimization

TP 399

A

2095-302X(2015)03-0444-08

2014-10-08；定稿日期：2014-10-30

国家自然科学基金资助项目(61373080, 61173174, 61103117)；济南市科技计划资助项目(201303011, 201302016, 201303021)

宁 阳(1985-)，男，山东莱芜人，硕士研究生。主要研究方向为图像处理、算法、计算几何。E-mail：polaris606@163.com

张云峰(1977-)，男，山东聊城人，教授，博士。主要研究方向为计算机辅助几何设计、图像处理。E-mail：yfzhang@sdufe.edu.cn