隐马尔可夫模型在生物信息学中的应用
黄 影
(西安文理学院数学与计算机工程学院,陕西西安 710068)
马尔可夫过程(Markov Process)是一种随机过程,其中每个时刻的状态形成了一个有限集合,且在已知目前状态(现在)的条件下,其未来的演变(将来)不依赖于自身以往的演变(过去)。马尔可夫链(Markov Chain)是一阶的马尔可夫过程,其中下一状态的概率分布只能由当前状态决定,在时间序列中其前面的事件均与之无关。在事件发展变化的过程中,从某种状态出发,下一时刻转移到其他状态的可能性,称为状态转移概率。在马尔可夫链中,所有状态都是直接可见的观察者,因此状态转移概率是唯一的参数。
隐马尔可夫模型(Hidden Markov Models,HMMs)是含有隐含未知参数的马尔可夫链[1-2]。HMMs由有限个状态组成,每一个状态都以一定的概率出现,状态之间的转换由转换概率表决定,每一个状态均可产生一个观察到的状态,在隐马尔科夫模型中,只有观察到的状态可见,真实的马尔科夫状态链不可见,因此被称为隐马尔科夫模型。
HMMs早期在自然语言处理领域获得了良好的应用[3],比如开始时用于语音识别[4],后来又用于音乐旋律分类[5]。随着HMMs的发展,现今在计算生物学和生物信息学中,也成为了经常被使用的模式识别(或机器学习)方法[6-7]。很多情况下,生物序列分析就是为每个残基(或核苷酸)赋予合适的标签,从而发现生物序列所具有的生物意义[8]。
1HMMs概念
1.1 一个例子
如图1所示,5-分位点识别问题是从基因发现问题中提炼出来的一个简单举例[1],用以引出对HMMs的介绍。假设给定一个DNA序列,其的起始部分是若干个外显子(Exon),然后是一个5-分位点,最后的部分是若干个内含子(Intron)。5-分位点相当于外显子与内含子的分界限,或者是从外显子转化为内含子的开关。这样,当前的问题就是识别出5-分位点的位置。
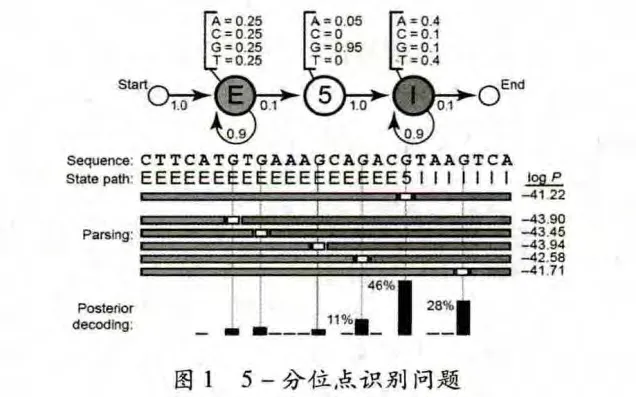
图1 5-分位点识别问题
以上边的信息为基础,可设计一个马尔可夫模型,如图1的上半部分所示。这个马尔可夫模型包含3个状态,分别对应赋予给碱基的3个标签:状态E(Exon),状态5(5-分位点)和状态I(Intron)。每个状态都有转移概率,相应的转移概率从当前状态移动到下一状态。转移概率的大小表示转移到下一状态的可能性的大小,因序列的前半部分都是E状态,中间是5状态,后半部分都是I状态,所以状态E和状态I到达自身的转移概率要大一些(0.9)。
然而,只依靠马尔可夫模型还不能推测出序列各个碱基对应的标签。想要较好地推测出5-分位点的位置,则不同的DNA序列一定具有不同的统计属性。这里做一些简单的假设:外显子对应的碱基呈均匀分布(即A,G,C,T出现的概率均为25%),内含子对应的碱基中有较多的A和T(A和T各占40%,C和G各占10%),令5-分位点对应一个固定的碱基G。
接下来引出HMMs。用上述马尔可夫模型产生一个状态序列。每生成一个状态,用其发射一个碱基。每种状态发射碱基的概率分布已在上边做了假设,称之为发射概率。然后,用马尔可夫模型的状态转移概率产生下一个状态。由此生成了两个序列信息,一个是状态路径,一个是观测序列(DNA序列)。在求解的问题中,观测序列是已知的,状态路径(标签序列)是未知的(隐藏起来的)。这样,在马尔可夫模型的基础上,包含发射概率分布的模型就是一个HMMs。
这样,要设计一个HMMs,就是要确定4方面的信息:(1)符号表(例如,在DNA序列中符号表中有4个元素AGCT。(2)状态集合,M。(3)每个状态i的发射概率ei(x),满足概率率∑xei(x)=1。(4)每个状态i到达状态j的转移概率ti(j),满足概率率∑jti(j)=1。任何具有这些属性的模型就是HMMs。
1.2 HMMs的3个计算问题
(1)解码问题。在序列分析问题中,给定的DNA序列是观测序列,我们要求解隐藏的状态路径。诸多潜在的状态路径都能产生出相同的观测序列,这样就需要找出具有最高概率的状态路径,这就是HMMs的解码问题。概率P(S,π HMM,θ)表示了具有参数θ的HMM的状态路径S能产生出观测序列π的概率,在求解时要用到θ中所有的转移概率和发射概率。例如,在图1中,观测序列有26个碱基,图的中间部分是6个潜在的状态路径,每个状态路径对应27个转移概率和26个发射概率。把这53个概率乘在一起,就得到了P(S,π HMM,θ)的值。为了便于比较,对每个计算结果进行取对数操作,可发现结果为-41.22的状态路径是最高概率的状态路径,也即5-分位点最有可能出现在第5个G的位置。
然而,对于大多数问题,存在诸多潜在的状态路径,文中无法将其一一进行枚举。基于动态规划思想的Viterbi算法[2]可高效地找出概率最高的状态路径。
此外,解码问题还有另外的一个形式—后验解码问题,即找到某个位置处具有最高出现概率的状态,最常用的算法是后验解码算法[2],原理是利用前向(Forward)和后向(Backward)两个动态规划算法对所有可能的路径进行累加。例如,在图1中,6个潜在的状态路径对应的P(S,π HMM,θ)值相差较小,若要确定其中哪个最有可能是真实的状态路径。可分别计算6个位置处被标识为状态5的概率,这就是后验解码问题。图1的下侧分别给出了这6个位置被标识为状态5的概率,其中概率值最大的为46%(对应于P(S,π HMM,θ)值等于-41.22的状态路径),其明显高于其他位置的概率,因此可以肯定P(S,π HMM,θ)值等于-41.22的状态路径是最接近于真实情况的状态路径。
(2)估值问题。估值问题是计算某个HMMs能生成给定观测序列的可能性。比如图1中的HMMs,用其的转移概率和发射概率分布,来求解生成给定的DNA序列的概率就是估值问题。从另一个角度来看,给定一个HMMs模型与一个观测序列,估值问题就是衡量这个HMMs对观测序列适用性的好坏。
估值问题常用的算法是前向(Forward)算法[2]和后向(Backward)算法[2],其均是精确的算法,一个是从序列的前边开始计算,一个是从序列的后边开始计算。在估值问题中,选取一个算法即可,因为前向和后向算法得到的结果相同。但在后验解码问题中需要同时使用这两个算法,即要计算位置的左边使用前向算法,右边使用后向算法。
(3)学习问题。在图1的例子中,所采用的是假设的参数,用估值问题可衡量这些参数对给定序列的适用性,若果适用性较差,需对假设的参数进行更新,使新的HMMs对给定序列的适用性变强,这个参数更新的过程就是HMMs的学习问题。
解决学习问题,常用的算法是BW算法[2],也称为前向-后向算法,是一个广义期望最大化问题。BW算法是EM算法的一个特例,即每次迭代包括一个E步与一个M步。假设有N条观测序列,每条序列的长度为L,且HMM模型有K个状态,则可分析出每次迭代的时间复杂度是O(3NK2L)。
2 HMMs在生物信息学中的应用
2.1 序列比对
序列比对(Alignment)是为了确定两个或多个序列之间的相似性,而将其按照一定的规律进行排列。为了能将多个序列排列在一起,序列中可插入间隔,一个或多个连续的‘-’称为gap。对两个序列进行比对,称为双序列比对,对多个序列进行比对称为多序列比对。本节重点讨论双序列比对,且无特别说明,后文中的序列比对均指双序列比对。
在序列比对问题中引入HMMs的方法如下。首先,序列比对最经典的精确算法是基于动态规划的算法。这个动态规划算法可转化为一个有限自动机。在动态规划算法的每步决策中,实际上是从3种选择中计算出当前的最优解。则整个动态规划算法的多步决策过程,就相当于状态间的不断转移,从而形成了一个拥有3个状态的有限自动机的状态转移链。动态规划算法求解的是状态转移的路径,由此,可将其转化为HMMs的解码问题。有了状态转移路径,通过适当的添加一些间隔,便可完成两个序列的比对。
这样,HMMs的状态集中有3个元素,字符表中有A,G,C,T这4个元素,并初始化一组参数,即状态转移概率和发射概率。区别于基因发现问题,现在状态序列发射的不是一条DNA序列,而是两条DNA序列,求解序列比对的HMMs如图2所示。

图2 序列比对的HMMs模型
图2中定义了HMMs的3个状态M,X,Y和状态转移概率。M表示比较操作,用于发射两个字符,第一条序列 x 中的 x[i],第二条序列y 中的y[j],且发射概率为 p(x[i]y[j]);X 表示插入操作,用于发射一个字符,即第一条序列x中的x[i],第二条序列中添加一个间隔‘-’,且发射概率为q(x[i]);Y表示删除操作,用于发射一个字符,即第二条序列x中的x[i],第一条序列中添加一个间隔‘-’,且发射概率为q(y[j])。此外,在实际比对结果中,不应出现如下情况:第一条序列的位点i处是‘-’,紧接着在第二条序列的位点i+1处也是‘-’。因此,模型中不允许状态X与状态Y之间进行相互转化。
有了HMM模型后,进行两条序列的比对就是HMM的解码问题,即用Viterbit算法求解出最有可能发射出两条输入序列的状态序列。求解出状态序列后,根据3种状态的发射功能,得出经过序列比对之后的两条序列。假设允许模型中的3个状态间能相互转化,则可对文献[7]中的模型进行修改。图3给出了经修改后的模型,设计思路是要尽量消除序列比对中可能出现的如下情况:第一条序列的位点i处是‘-’,紧接着在第二条序列的位点i+1处也是‘-’。
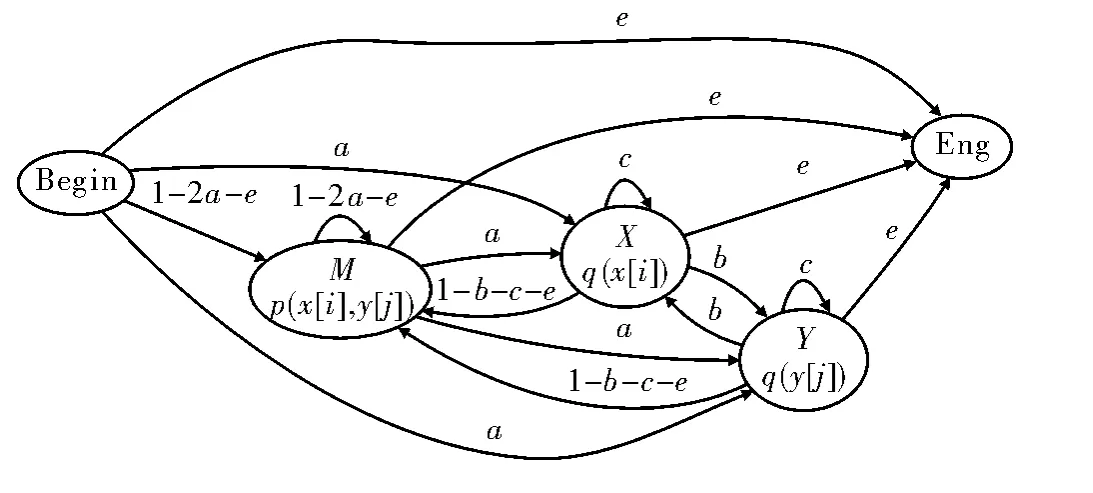
图3 修改后的序列比对HMMs模型
图3中参数设定如下:从其余状态到只发射一个字符的状态的转移概率记为a,即被标记成绿色的箭头;只发射一个字符的状态到其自身的转移概率记为c,即被标记成蓝色的箭头;所有状态到结束状态的转移概率记为e,即被标记成橙色的箭头。然后,在图3的模型中添加状态X与Y之间的转移概率,记为b,即被标记成红色的箭头。在实际中,将b值设置为较小的数,以表示出现一对‘-’的概率很小,也即两个序列中出现一对‘-’的罚分将很重。最后,计算其余的状态转移概率。计算原则是:从某个状态出发,到达其余状态的概率之和为1。例如从X到M的概率为1-b-c-e。
2.2 基因发现
基因发现是在一个DNA序列中查找基因,但更通用的一个说法是为DNA进行标签,比如将其标识为coding、intergenic、introns等区域。因此,基因发现常被认为是生物信息学中序列标签问题的一个特例。上文中的例子就是DNA标签的一个简单的抽象,所以不再展开讲解基因发现的HMMs。Krogh等人在基因发现问题中引入了 HMMs[9],用以区分 E.coli基因中的coding区域和intergenic区域。
随后的用于基因发现的HMMs都是对Krogh等人工作的扩展。例如,Henderson等[10]设计了独立的HMM模块,使得每个模块适用于一个特定的DNA区域。Kulp 和 Burge等[11-12]使用一个特殊的 HMM(GHMM 或“hidden semi-Markov model”),使得每个内部状态点可发射多次。近年来,研究者更关注于在基因组范围内进行基因预测,并设计相应的HMMs[13]。
2.3 其他的一些应用
多序列比对(Multiple Alignment)经常用于评估一个新的序列是否属于一个已知的同源序列家庭。多条序列可构成一个谱(Profile),即一个位置权重矩阵。多序列比对往往采用”Profile HMM”技术,HMM的构造原理(状态转移)类似于双序列比对的模型。对于多序列比对问题,HMMs是公认的强有力的工具。但HMMs的训练非常耗时,所以通常采用启发式方式进行训练。近年来,模拟退火、粒子群算法等进化算法被用于求解多序列比对的HMMs的训练中[14-15]。
系统发生分析(Phylogenetic Analysis)。系统发生分析的目标是寻找系统发生的概率模型并得到不同物种的进行树。为解释序列各个位置间进化速度的变化,Felsenstein等将3个可能的速度值做为HMM的状态[16]。Thorne等提出了一个使用HMMs的进化系统发生模型,将主要结构与一个已知或待评测的二级结构合并[17]。最近,Bykova等对 HMMs进行了改进,用以解释当显著的特种不确定时的特例[18]。
基因映射(Genetic Mapping)。使用一个非平稳的HMM进行基因映射,是生物信息学中最早的HMMs应用,即在染色体中已知次序的轨迹间对一些距离进行评估。初始的时候,Lander等基于谱系得到基因间的链接映射[19]。后来,为了得到辐射谱,Slonim等运用了一个基于实验辐射数据的非平稳HMM[20]。随着高通量测序的发展,已有不少的学者关注于基于下一代测序数据的用于基因映射的非平稳HMM[21]。
蛋白质二级结构预测(Secondary Structure Protein Prediction)。HMMs也应用到了预测一个蛋白质的二级结构,即预测局部三维结构的类型,这是预测全局三维结构非常重要的一步[22]。一个标准的HMM可被看作一个随机的“正则语法”。基于此,Eddy等引入了结合协方差方法的 HMMs[23-24]。
信号肽预测(Signal Peptide Prediction)。信号肽预测就是确定蛋白质在缩氨酸第一区域中的目标地址,通常对于疾病分析和药物研制有重要意义。非常成功的一个方法就是使用一个标准的HMMs在革兰氏阴性的真细菌中预测脂蛋白信号缩氨酸[25]。Schneider等综述了基于HMMs的信号肽预测的3个其他方法[26]。
横跨膜蛋白质预测(Transmembrane Protein Prediction)。当前直接测量一个横跨膜蛋白质的3D结构几乎是不可行的。一些研究者专门研究预测螺旋形横跨膜蛋白质拓扑结构的 HMMs[27-28]。另外一些研究者则专门研究预测β-胡萝卜素横跨膜蛋白质的拓扑结构的 HMMs[29-30]。
抗原决定基预测(Epitope Prediction)。免疫反映中的一个前提步骤是将一个抗原决定基绑定到一个I类或II类MHC微粒。然而,大多数抗原决定基并不能绑定到MHC微粒,所以能预测出哪个抗原决定基能够进行绑定是重要的。Mamitsuka等使用无监督学习来提升HMMs的性能[31],既适用于I类也适用于II类MHC微粒。
3 结束语
本文讨论了隐马尔可夫模型(Hidden Markov Models,HMMs)在生物信息学中的应用情况。介绍了HMMs,并分析了如何在生物信息学中设计和应用HMMs。随着生物实验技术的不断发展,生物学家收集的实验数据的种类越来越多、数据量越来越大,而实验分析技术和计算方法明显发生了滞后。因此,虽然当前HMMs已在一些生物信息学领域中得到了良好的应用,但其不乏有更广泛的应用空间,本文旨在为HMMs的初学者提供一个快速的学习途径。
随着生物信息学的快速发展,会不断涌现新的应用。必然需要新的模型结构以适应新的生物信息学问题。鉴于隐马尔科夫强大的适应能力,其可与其他模型相应结合,这些模型如贝叶斯、神经网络、支持向量机、乔姆斯基文法等,在未来的生物信息学应用中继续发挥更大的作用。
[1] Eddy S.What is a hidden Markov model[J].Nature Biotechnology,2004,22(10):1315 -1316.
[2] Duta R O.Pattern classification[M].Beijing:China Machine Press,2004.
[3] Charniak E.Statistical techniques for natural language parsing[J].AI Magazine,1997(18):33 -43.
[4] Singh B,Kapur N,Kaur P.Speech recognition with hidden Markov model:a review [J].International Journal of Advanced Reasearch in Computer Science and Software Engineering,2012,2(3):401 -403.
[5] Pollastri E,Simoncelli G.Classification of melodies by composer with hidden Markov models[C].Florence,Italy:the First International Conference on Web Delivering of Music WEDELMUSIC’01,2001.
[6] Valeria D F,Filippo A P,Valerio P.Hidden Markov models in bioinformatics [J].Current Bioinformatics,2007(2):49-61.
[7] Yoon B.Hidden Markov models and their applications in biological sequence analysis [J].Current Genomics,2009(10):402-415.
[8] Durbin R,Eddy S.Biological sequence analysis:probabilistic models of proteins and nucleic acids[M].Cambridge,UK:Cambridge University Press,1998.
[9] Krogh A.Computational methods in molecular biology[M].Amsterdam,Holland:Elsevier Press,1998.
[10] Henderson J,Salzberg S,Fasman K H.Finding genes in DNA with a hidden Markov model[J].Journal of Comput Biology,1997(4):127 -141.
[11] Kulp D,Haussler D,Reese M G,et al.A generalized hidden Markov model for the recognition of human genes in DNA[C].Menlo Park,California:International Conference on Intelligent Systems in Molecular Biology,1996.
[12] Burge C B,Karlin S.Finding the genes in genomic DNA[J].Current Opin Structer Biology,1998(8):346 -354.
[13] Testa A C,Hane J K,Ellwood S R,et al.Coding Quarry:highly accurate hidden Markov model gene prediction in fungal genomes using RNA - seq transcripts[J].BMC Genomics,2015(16):170 -175.
[14] Sun J,Wu X,Fang W,et al.Multiple sequence alignment using the hidden markov model trained by an improved quantum - behaved particle swarm optimization[J].Information Sciences,2012,182(1):93 -114.
[15] Sun J,Palade V,Wu X,et al.Multiple sequence alignment with hidden Markov models learned by random drift particle swarm optimization [J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2014,11(1):243-257.
[16] Felsenstein J,Churchill G.A hidden Markov model approach to variation among sites in rate of evolution[J].Molto Biology Evolution,1996(13):93 -104.
[17] Thorne J,Goldman N,Jones D.Combining protein evolution and secondary structure[J].Molto Biology Evolution,1996(13):666-673.
[18] Bykova N A,Favorov A V,Mironov A A.Hidden Markov models for evolution and comparative genomics analysis[J].PLoS One,2013,8(6):e65012 - e65017.
[19] Lander E,Green P.Construction of multilocus genetic linkage maps in humans[J].Proceeding of Natl Acad Science,1987(84):2363-2367.
[20] Slonim D,Kruglyak L,Stein L,et al.Building human genome maps with radiation hybrids[J].Journal of Computational Biology,1997(4):487 -504.
[21] Zamanzad G F,Jürgen C,Tomasz B.A nonhomogeneous hidden Markov model for gene mapping based on next-generation sequencing data[J].Journal of Computational Biology,2015,22(2):178 -188.
[22] Yoon B,Vaidyanathan P.HMM with auxiliary memory:a new tool for modeling RNA secondary structures[C].Monterey,CA:the Thirty - Eighth Asilomar Conference on Signals,Systems and Computers,2004.
[23] Eddy S,Durbin R.RNA sequence analysis using covariance models[J].Nucleic Acids Research,1994(22):2079 -2088.
[24] Eddy S.A memory- efficient dynamic programming algorithm for optimal alignment of a sequence to an RNA secondary structure[J].BMC Bioinformatics,2002(2):3 -18.
[25] Juncker A,Willenbrock H,Von Heijne G,et al.Prediction of lipoprotein signal peptides in Gramnegative bacteria [J].Protein Science,2003(12):1652 -1662.
[26] Schneider G,Fechner U.Advances in the prediction of protein targeting signals[J].Proteomics,2004(4):1571 -1580.
[27] Sonnhammer E,von Heijne G,Krogh A.A hidden Markov model for predicting transmembrane helices in protein sequences[C].Montreal,Canada:International Conference on Intelligent Systems in Molecular Biology,1998.
[28] Tusnady G E,Simon I.Principles governing amino acid composition of integral membrane proteins:application to topology prediction [J].Journal Molto Biology,1998(283):489-506.
[29] Martelli P L,Fariselli P,Krogh A,et al.A sequence - profilebased HMM for predicting and discriminating beta barrel membrane proteins [J].Bioinformatics,2002(18):S46-53.
[30] Liu Q,Zhu Y,Wang B,et al.A HMM - based method to predict the transmembrane regions of beta-barrel membrane proteins[J].Computer Biology Chemistry,2003(27):69-76.
[31] Mamitsuka H.Predicting peptides that bind to MHC molecules using supervised learning of hidden Markov models[J].Proteins,1998(33):460 -474.

