两种SAR成像算法仿真比较

李明理，黄 月

(中国人民解放军91404部队92分队，河北秦皇岛 066000)

合成孔径雷达［1］是一种高分辨率雷达，具有全天候、全天时、远距离、高分辨成像的工作能力，它借助于脉冲压缩技术实现距离维的高分辨率，借助于方位多普勒分析技术实现方位维的高分辨率，现己广泛运用于环境保护、海洋观测、灾害预测等方面。

在合成孔径雷达系统中，雷达发射器连续发射线性调频脉冲信号，接收器则接收目标反射的回波信号，通过对回波数据进行处理以得到对所观测区域的目标分布图像。

目标距离向的信息是通过对所发射的线性调频信号的处理实现的。如果在某一距离存在目标，所发射的线性调频信号会被目标反射回来，用距离参考匹配滤波函数进行压缩处理可以使信号能量集中到目标所在的距离对应的时间点，从而实现对目标在距离上的成像。

方位向的成像由SAR雷达平台与目标间的距离变化的多普勒分析技术［2］来实现。在一定的限制条件下，相对运动的多普勒信号也是一个线性调频信号，这样可以用和距离向成像同样的处理方式实现方位向上的成像。

根据SAR系统的不同目的，可以采用不同的成像算法。一般的SAR成像算法［3－4］有时域相关卷积和频域相乘两种，本文对这两种算法进行仿真比较研究。

1 两种成像算法比较

基于时域相关卷积和基于频率相乘的SAR成像处理流程［5］图如图1所示。

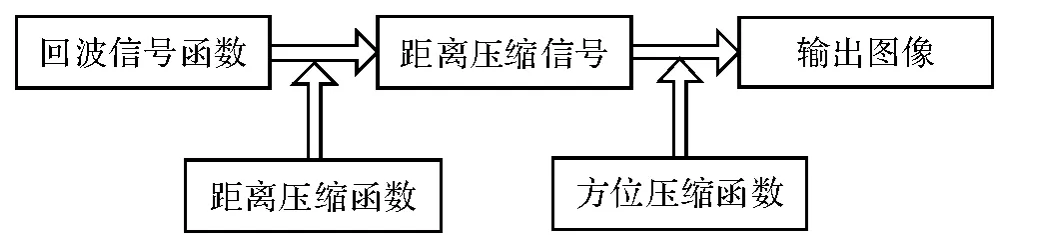
图1 SAR成像算法处理流程图

由于在距离向和方位向的匹配滤波算法一致，因此算法性能可通过直接在时域进行一维卷积实现匹配滤波，与通过傅里叶在频域(一维)相乘实现匹配滤波进行比较来实现。根据卷积公式可以得到用时域卷积实现匹配滤波的运算次数S1与卷积点数N的关系［6］如式(1)所示。

用频率相乘实现匹配滤波的计算量与N选取有关，因为快速傅里叶变换要求N是2的幂级数。当N为2的幂级数时的运算次数［7］为式(2)

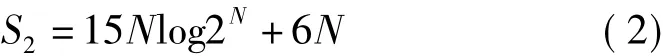
当不是2的幂级数，需要补充到大于且最接近的2的幂级数，但一定会＜2N，将N换成2N，则其运算次数少于式(3)

两种算法的运算量比较图如图2所示，图中S1为时域卷积运算量，S2为频率相乘最少运算量，S3为最大运算量。从图2(a)可以看到，在点数＜20(S1与S2交点)时，时域卷积计算量较少;点数在20和60之间时还需具体分析;在点数＞60(S1与S3的交点)时，频域相乘计算量较少。从图2(b)可以看到，N越大，频域相乘计算量相比时域卷积计算量越小，频域相乘法进行匹配滤波处理的优势更大。

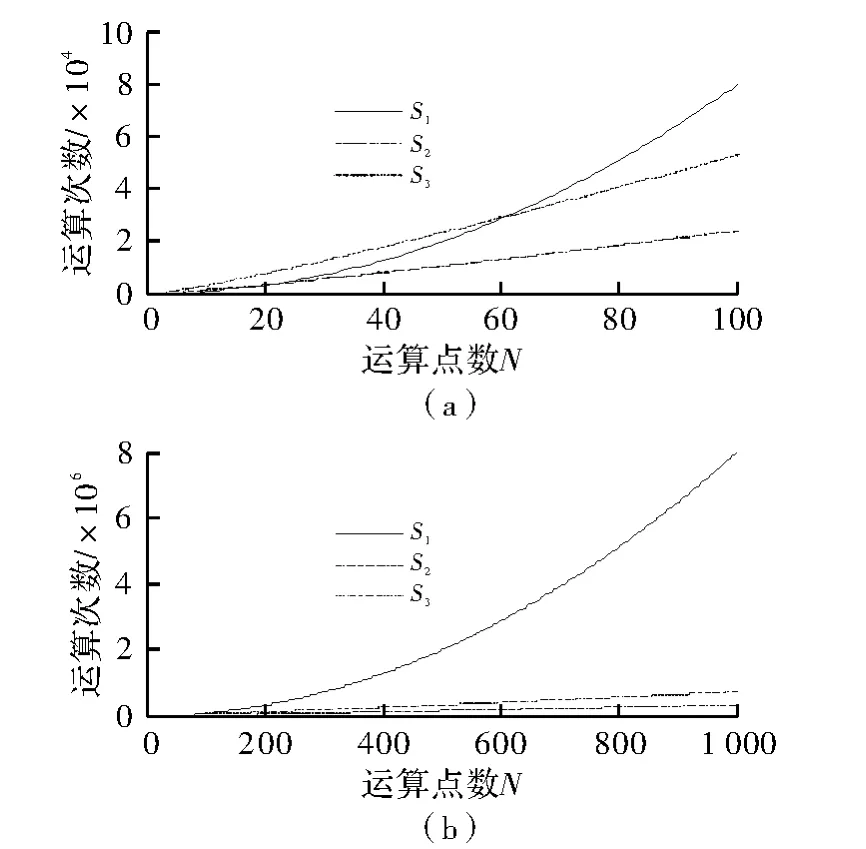
图2 一维时域卷积与频率相乘计算量比较图

以上是一维成像环境下两种算法的理论计算比较。在Matlab平台分别用时域卷积和频域相乘进行一维匹配滤波，在点数相同的情况下，比较其运行时间，得到图3所示结果。

图3 两种算法在Matlab平台运行时间图

图3所示的运行时间的比较和图2所示的运算量与点数N的关系相类似，点数较大时，频率相乘进行匹配滤波运算量较小，且N越大，运算量越小。实际运算中，点数一般较大［8］，因此以运算量和运算时间为标准，基于频率相乘进行匹配滤波的SAR成像算法更具有优势。

二维成像环境下时域卷积［9］和频率相乘得到的成像结果分别如图4和图5所示，成像点数为271×360;可以看出两者运行结果基本无差别，但运行时间分别是93.765 s、35.856 s，两者的比值为 2.615，即基于时域卷积的SAR成像算法运行时间是基于频域相乘的SAR成像算法的2.16倍，基于频域相乘的SAR成像算法运行时间较少。

图4 271×360点相关卷积

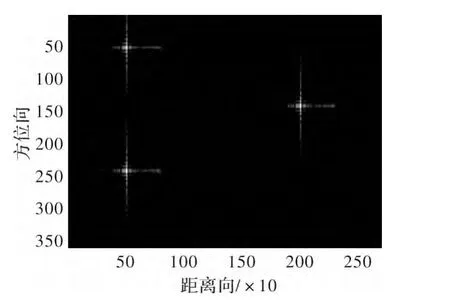
图5 271×360点傅里叶变换

改变成像点数的大小，用两种成像算法得到的运行时间如表1所示。

表1 两种成像算法的运行时间比较

由表1可见，运行时间变换与一维运行时间相似，频域相乘运行时间少于时域卷积运行所需时间，而且数据量越大，基于时域卷积的SAR成像算法运行时间是基于频域相乘的运行时间的倍数越大，故从运行时间上看，基于频域相乘的SAR成像算法优于基于时域卷积的SAR成像算法。

从以上的比较得出，基于频域相乘的SAR算法有运行时间上的优势，适于对实时成像要求较高的场合。基于时域卷积的SAR耗时较长，但其优点是只要得到一个相干积累长度的信号，单个方位上的像就可以得到，随着雷达平台的运动，每个方位上的像可以依次得到，这样可以实现动态成像。

2 结束语

对时域相关卷积和频域相乘这两种SAR成像算法进行仿真比较研究，得到频域相乘SAR成像算法在运行时间上比时域相关卷积更具优势;时域相关卷积可以实现动态成像。

［1］ 皮亦鸣，杨建宇，付毓生，等．合成孔径雷达成像原理［M］．成都:电子科技大学出版社，2007．

［2］ 保铮，邢孟道，王彤．雷达成像技术［M］．北京:电子工业出版社，2005．

［3］ 袁孝康．合成孔径雷达方程［J］．上海航天，2002(3):1－5，14．

［4］ 张直中．机载和星载合成孔径雷达导论［M］．北京:电子工业出版社，2004．

［5］ 董庆，郭华东．合成孔径雷达海洋遥感［M］．北京:科学出版社，2005．

［6］ 张澄波，电子学．综合孔径雷达:原理，系统分析与应用［M］．北京:科学出版社，1989．

［7］ Cumming I G，Wong F H，洪文．合成孔径雷达成像—算法与实现［J］．北京:电子工业出版社，2007．

［8］ 裘金飞．合成孔径雷达 (SAR)成像技术研究［D］．南京:南京理工大学，2005．

［9］ 李伟．合成孔径雷达目标成像仿真研究［D］．西安:西安电子科技大学，2010．