低周疲劳试验寿命预测模型分析及其对断口硬度影响

陈亚军，褚玉龙，杨旭东，吴 腾

（中国民航大学中欧航空工程师学院，天津 300300）

0 引 言

由疲劳导致的断裂破坏是机械失效的主要原因，也是工业领域中的常见事故。实际数据指出，约有50%～90%的机械结构的破坏属于疲劳破坏[1-3]。因此，对材料的疲劳行为和寿命预测的分析具有实际指导意义[4]。如今对材料疲劳裂纹的萌生、裂纹扩展和疲劳断裂的微观特征以及疲劳寿命的预测已有较深入的研究[5-6]，但其理论模型与实验相互验证及优化工作还有待提高[7]。

疲劳失效是当前科学研究和工程技术的主要方向之一，目前主流的理论一般将疲劳失效过程划分为裂纹形成与裂纹扩展两个时期。考虑裂纹扩展机制，通常使用断裂力学模型，其理论体系比较成熟且取得了大量研究成果。针对裂纹形成过程，现今已存两种试验分析思路：全程采用试验手段，进行与材料和部件的实际工况相同或相似的试验，以此获取试验数据，其优点为可靠性高，缺点是花费巨大、周期长；试验与统计经验相结合，通过使用已得到的标准试验结果，按照换算和修正方法来计算实际工况下的疲劳寿命。

复杂的失效模式使人们对疲劳全过程和规律的认识仍不清楚，准确进行疲劳寿命预测分析有很大困难。通过采用理论分析与试验研究相结合，对金属材料的疲劳损伤微观机制及其宏观物理模型进行研究意义重大。因此，本文对金属材料的疲劳损伤失效进行试验研究，以求进一步评测寿命预测模型，同时对疲劳断口的硬度变化规律进行实验探讨。

1 试验材料

试验用材料为国产45#钢，其成分的质量分数范围如表1所示。密度7.85g/cm3，弹性模量210GPa，泊松比0.269。GB/T 699——1999《优质碳素结构钢》规定 45#钢抗拉强度为 600 MPa，屈服强度为355MPa。

表1 45#钢的典型化学成分质量分数 %

按GB/T 15248——1994《金属材料轴向等幅低循环疲劳试验方法》的要求，设计试样的直径为10mm，夹持端直径为20mm，试样平行段长度为30mm，既能保证测量准确度又可以保证试验中受载时保持稳定。具体试样尺寸参数如图1所示。

图1 疲劳试验试样尺寸（单位：mm）

2 试验内容、结果及分析

2.1 寿命预测模型分析及对比

2.1.1 试验内容

采用Instron 8803液压伺服疲劳机（最大载荷500 kN），使用轴向总应变控制，应变比R=-1，应变幅选±0.5%，±1.0%，±1.2%，±1.5%，±2.0%5 个应变水平，波形为三角波，试验频率为0.33Hz，试验温度为室温20℃，试验数据采集由计算机完成，各试样均进行到断裂为止。

2.1.2 试验结果及讨论

在研究疲劳寿命预测时分别采用Manson-Coffin方程[8-9]、拉伸迟滞能模型[10-11]、三参数幂函数能量法建立疲劳寿命预测模型。Manson-Coffin方程中将总应变程分解为弹性应变程和塑性应变程，分别与循环破坏数呈对数线性关系：

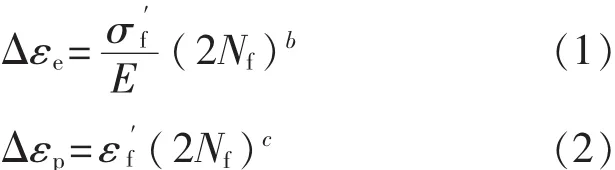
拉伸迟滞能模型中，假设低周循环疲劳的损伤[12]以试样的拉伸滞后能为参量，由损伤参数来表达：拉伸迟滞能ΔWt为非弹性应变程Δεin和峰值拉伸应力σs的乘积，即：

迟滞能与寿命之间呈幂指数关系：

式中α为常数。

三参数幂函数能量法综合Manson-Coffin方程和拉伸迟滞能模型的分析方法，采用能量表征参量来进行寿命预测。通过循环载荷过程中的应力-应变滞后环提取的非弹性应变滞后能，并将其与疲劳极限、寿命联系建立表达式：

滞后能与寿命之间呈幂指数关系：

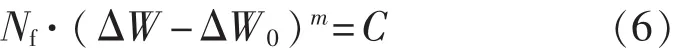
式中m，C为常数。

根据以上各个寿命预测模型的参量计算方法，通过试验记录数据，可以得到疲劳实验结果，如表2所示。

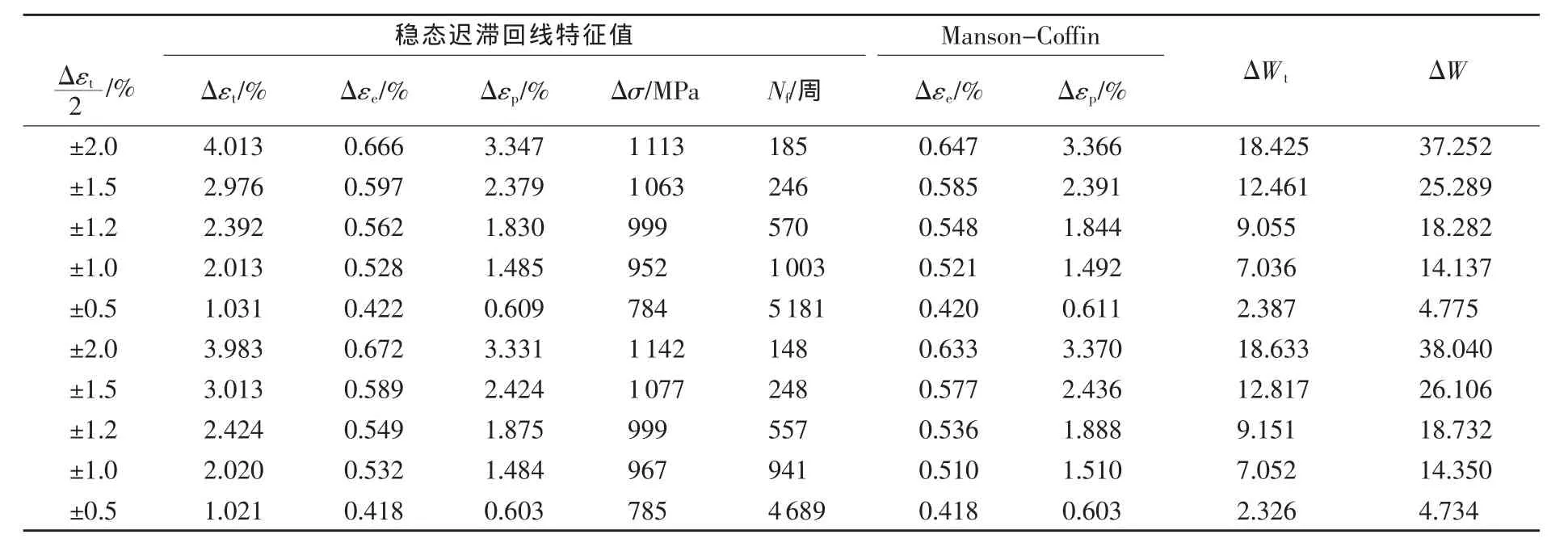
表2 各寿命预测模型表征参量计算值

根据不同应变幅对应的平均寿命值画出寿命随应变幅值变化曲线，如图2所示，可以发现随着应变幅从±0.5%增大到±2.0%，材料的平均疲劳寿命从4935减小到167，呈递减趋势。

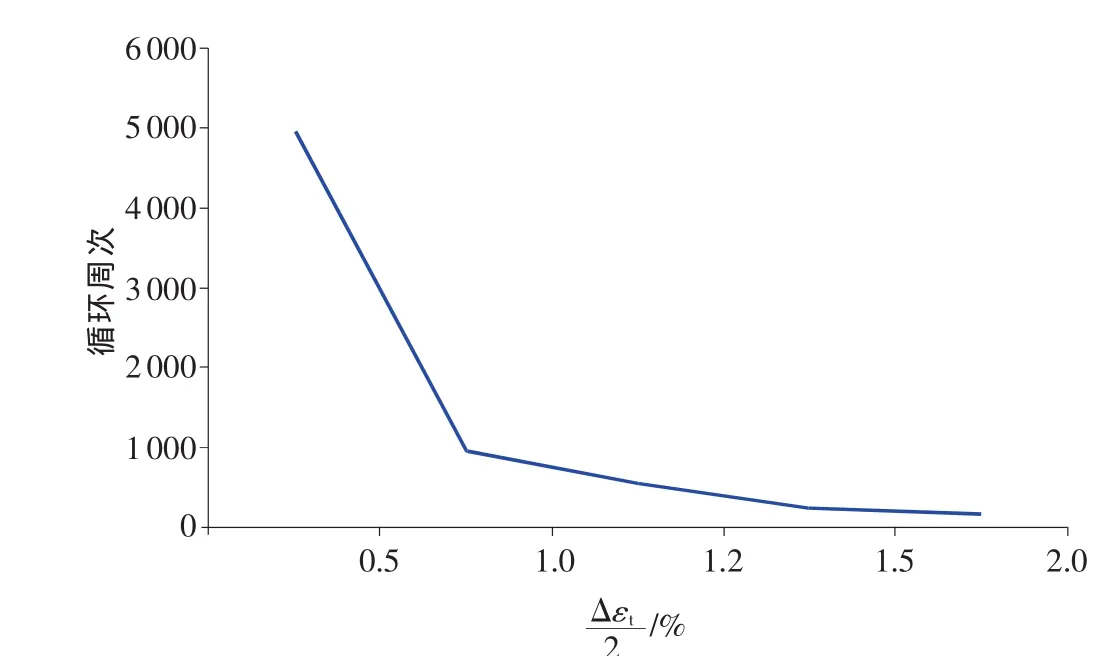
图2 疲劳寿命随应变幅值变化关系

对表2中的疲劳试验结果进行处理，可以得到3个寿命预测模型的参数和预测方程。

Manson-Coffin预测方程：

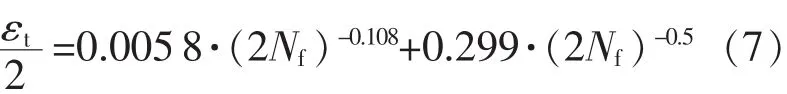
拉伸迟滞能模型预测方程：

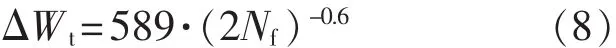
三参数能量法预测方程：

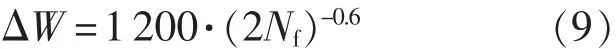
使用分散带和标准差两个统计量来评价3种疲劳寿命预测模型的预测能力，结果如表3所示。

由表可知，拉伸迟滞能损伤函数法和三参数幂函数能量法的评测结果的分散带和标准差数值相近，其中后者的预测准确度更高。这是因为前者更适用于应力均值不为零的情况，考察平均应力对疲劳寿命的影响，对于低周对称循环疲劳并没有发挥其优势；而后者综合考虑了Manson-Coffin方程和迟滞能损伤函数法的优缺点，在确定稳态滞后环特征塑性应变程时不再使用公式计算，而是直接读取记录曲线。使用能量作为表征参量，与应力或应变历程关系不大，物理意义更加明确。因此，对于45#钢而言，在基于应变控制模式的疲劳寿命估算方法当中，三参数幂函数能量法具有更加广泛的适用性和合理性。

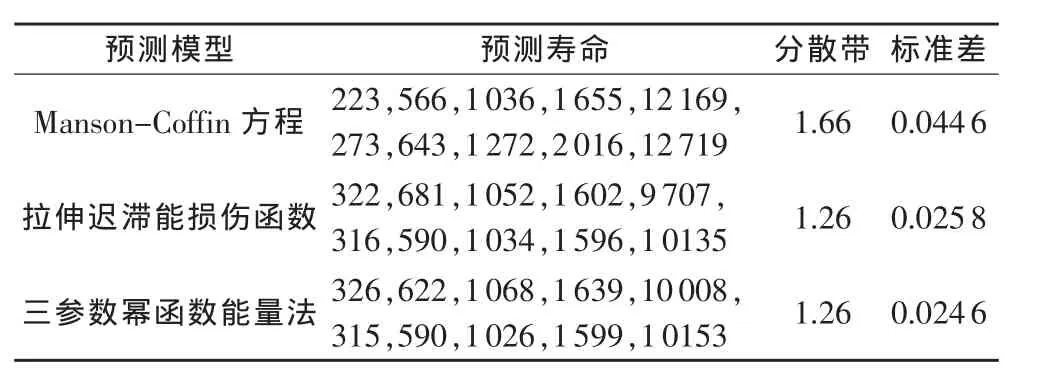
表3 寿命预测能力评测结果

2.2 断口微观形貌分析

将试样断口附近区域切割成高度为10mm的柱形体，然后用Hitachi S-3400N扫描电子显微镜观察±0.5%和±2.0%应变幅下疲劳断口全貌，进行对比分析。

观察±0.5%应变幅下疲劳断口试样放大11倍的扫描电镜照片，如图3（a）所示，可以发现断口的疲劳裂纹沿箭头方向扩展，并且疲劳过程经历3个区域：左侧部分平整度很好，为疲劳源区；中间部分出现以疲劳源为圆心的环线，为疲劳裂纹扩展区；右侧表面粗糙不平，起伏很大，为裂纹失稳断裂区。

图3（b）为疲劳源区微小裂纹放大至500倍的扫描电镜照片，可以看到箭头指示部位产生裂纹。对疲劳裂纹扩展区局部放大至100倍，可以发现断口表面很光滑，少量出现微小裂纹，如图3（c）所示。这是由于循环的拉压过程中，当材料受到压缩载荷时，已分离的上下表面互相挤压、摩擦，导致平整度升高。

图4 ±2.0%应变幅疲劳断口扫描电镜照片

观察±2.0%应变幅下疲劳断口试样放大11倍的扫描电镜照片，如图4（a）箭头所指，可以看到断口的疲劳裂纹扩展区。对疲劳断口边缘部位放大至500倍，如图4（b）所示，可以看到沿光滑截面发展的裂纹，并且扩展方向与表面相垂直。对疲劳源区微小裂纹放大至500倍，如图4（c）所示，可以看到箭头指示部位微小裂纹扩展互相连接形成长裂纹的趋势。

对比图 3（a）与图 4（a），发现±2.0%应变幅下疲劳断口比±0.5%应变幅下疲劳断口疲劳源区特征更加明显，疲劳扩展区面积更小，微小裂纹和缺陷的的数量明显增多、微小裂纹互相连接并且扩展长度更大。说明大应变幅对材料内部结构所造成的损伤更为严重；疲劳裂纹源自表面开裂或者内部夹杂物，造成局部应力集中，进而微小裂纹扩展至长裂纹。

2.3 疲劳对材料断口硬度变化的影响

2.3.1 试验内容

选取5个不同应变幅下疲劳失效后的试样，取高度为10 mm的柱体进行打磨、抛光、超声波清洗后，使用Matsuzawa显微硬度计分别沿径向和轴向进行显微硬度试验。径向硬度测试即从截面中心附近为起点，每间隔0.25 mm作硬度测试，共15个硬度测试点，最后一点位于边缘附近，测得材料在原始状态，以及±0.5%、±1.0%、±1.2%、±1.5%、±2.0%应变幅下的疲劳断口硬度值随径向距离的变化，如表4所示（试验选用载荷值为4903mN，低倍物镜放大倍数40，高倍物镜放大倍数200）。

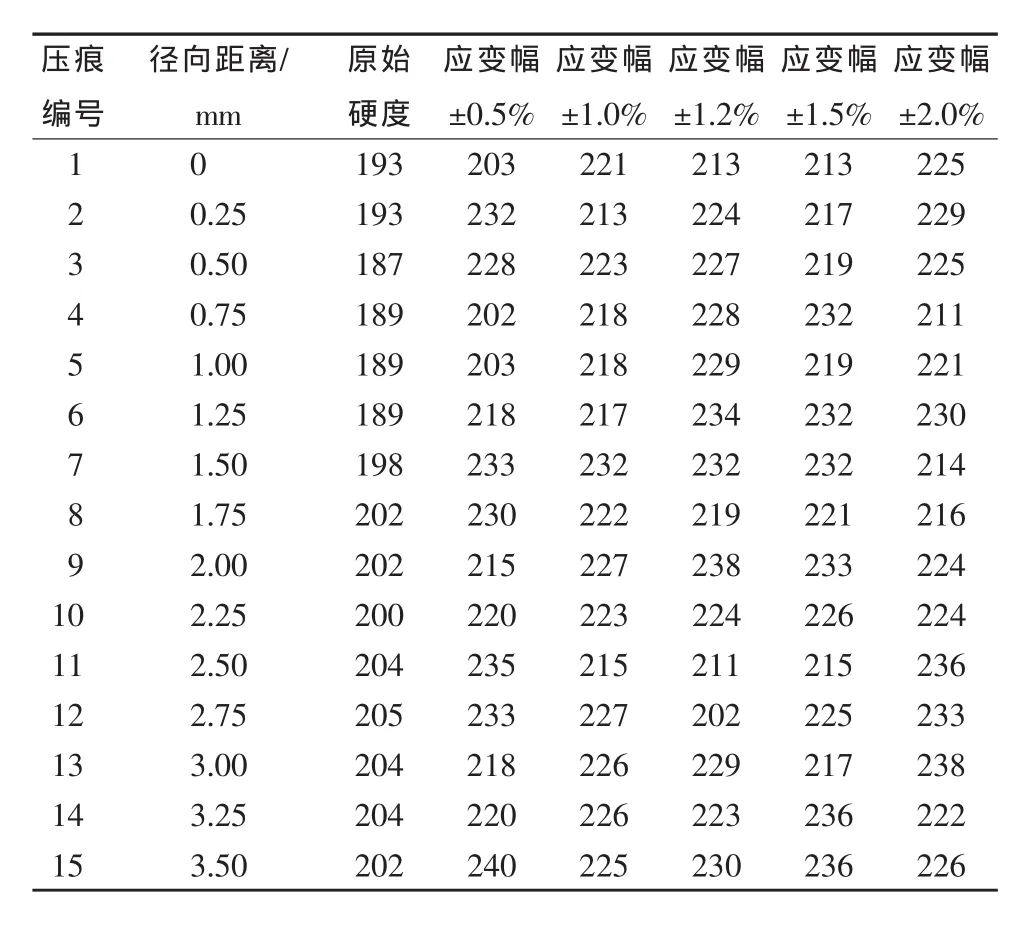
表4 不同应变幅下的疲劳断口硬度值随径向距离的变化

轴向硬度试验选取±1.2%应变幅显微硬度试样，从截面位置开始做第一个测试点，在试样的侧面沿轴向同样每间隔0.25mm选择一个位置作为硬度测试点，测量15个点的硬度，材料在±1.2%应变幅疲劳断口硬度值随轴向距离的变化如表5所示。

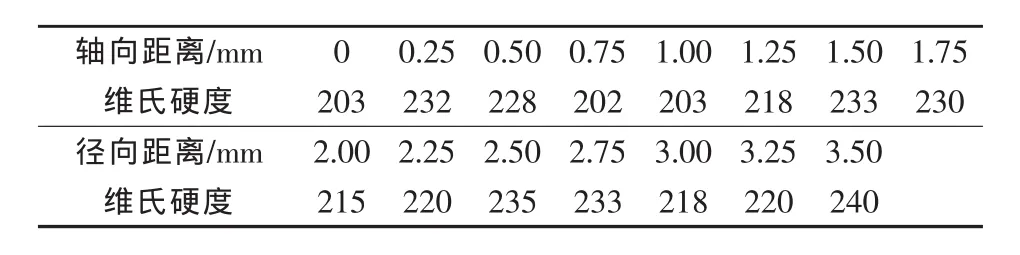
表5 ±1.2%应变幅下硬度值随轴向距离变化

2.3.2 实验结果及讨论

1）硬度值随断口截面径向位置变化关系。根据表4数据，可以作出不同应变幅下断口截面上硬度随径向距离变化的曲线，如图5所示，可以发现硬度值沿径向呈振荡增大趋势。

根据表4中原始材料硬度值随径向距离的变化可以作出截面上硬度随径向距离变化的曲线，如图6所示。

可以发现，45#钢原始材料的硬度值比较均匀，沿截面的径向距离变化不大，平均值在200左右。将5个不同应变幅下，每个对应位置的硬度值取平均，可以得到疲劳后材料的平均硬度随径向距离的变化曲线，如图7所示。将材料对应位置的平均硬度值拟合成直线，其方程为

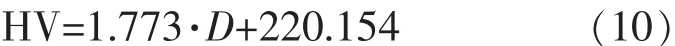
式中：HV——维氏硬度值；

D——压痕点到中心的径向距离。

图5 不同应变幅下硬度随径向距离变化

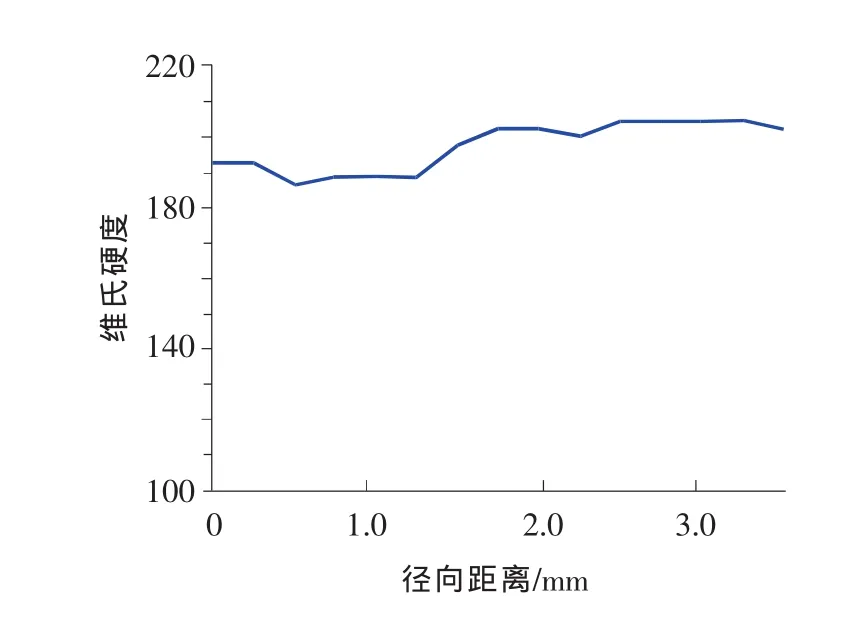
图6 45#钢原始材料硬度随径向距离变化

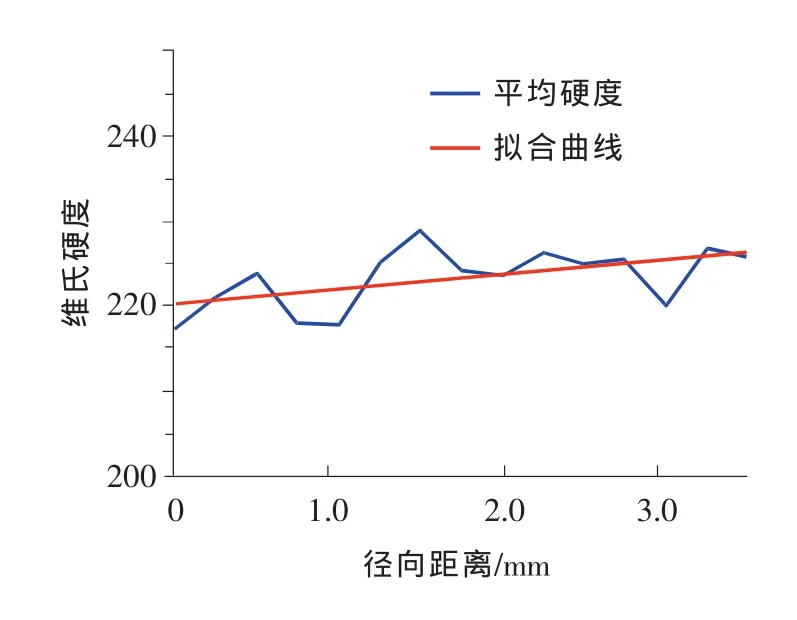
图7 平均硬度随径向距离变化

可以看出，材料的硬度值随着其位置到中心的径向距离增大而增大，总体趋势很明显，并且表现出一定波动，这是由材料本身的不均匀造成的。

2）硬度值随断口侧面位置变化关系。根据表5数据，可以作出断口侧面上硬度随轴向距离变化关系的曲线（见图8），可以发现硬度值沿轴向呈振荡变化，没有明显趋势，说明疲劳加载对断口侧面不同位置所造成的强化作用差异很小。

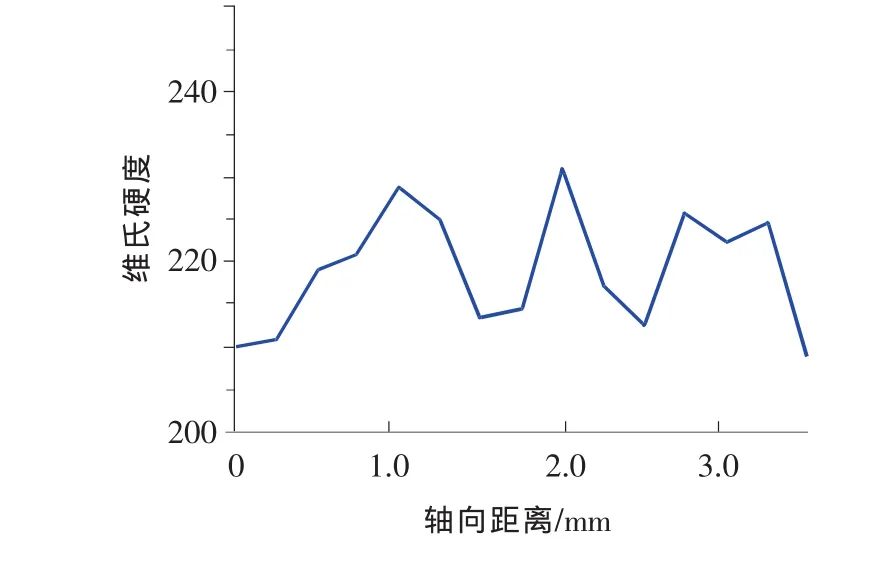
图8 ±1.2%应变幅下侧面硬度随轴向距离变化

3）硬度值随应变幅变化关系。平均硬度值随不同应变幅的变化如图9所示。由于低周疲劳作用使得断口附近的材料发生强化，可以发现平均硬度值随着应变幅的增加而增大。

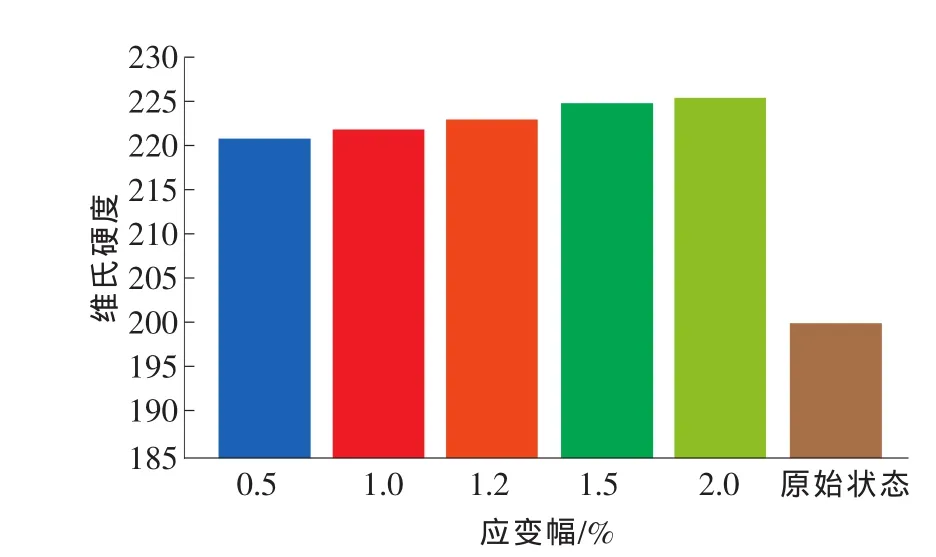
图9 原始材料与不同应变幅疲劳后平均硬度对比

将原始材料的硬度与不同应变幅下疲劳后平均硬度对比，可以发现，经过疲劳过程后，45#钢断口附近的力学性能变化，体现在平均硬度上，表现为硬度值由初始状态的平均值200左右升至平均值220左右。

3 结束语

1）在其他疲劳实验参数固定的情况下，随着应变幅从±0.5%增大到±2%，材料的平均疲劳寿命从4935减小到167，呈递减趋势。通过对3种寿命评测，三参数幂函数能量法得到分散带在1.26以内，标准差在0.0246以内。因此，对于45#钢而言，在基于应变控制模式的疲劳寿命估算方法当中，三参数幂函数能量法具有更加广泛的适用性和合理性。

2）对不同应变幅值疲劳断口近截面沿径向及轴向进行显微硬度测试，发现断口径向硬度值沿近中心位置至边缘呈波动增大趋势，而轴向硬度值随着离断口距离增大的变化不大；经过疲劳强化后，断口径向截面平均硬度值为220左右，高于原始状态截面平均硬度值200，且随着应变幅值增大，断口径向截面的平均硬度值呈一定程度的递增趋势。

[1] 伍颖.断裂与疲劳[M].武汉：中国地质大学出版社，2008：29.

[2] Wahab M A，Alam M S.The significance of weld imperfections and surface peening on fatigue crack propagation life butt-welded joints[J].Mater Process Technol，2004（153）：931-937.

[3] Han Q， Lavernia E J， Mohamed F A.Dislocation structure and deformation in iron processed by equal-channel-angular pressing[J].Metall Mater，2004，35（4）：1343-1350.

[4] Amaro R L，Rustagi N， Findley K O，et al.Modeling the fatigue crack growth ofX100 pipeline steelin gaseous hydrogen[J].International Journal of Fatigue，2014，59（2）：262-271.

[5] 张珂，吴园园，董登超.20#钢管外折缺陷的原因分析及对策[J].中国测试，2013，39（5）：28-30.

[6] 何柏林，王斌.疲劳失效预测的研究现状和发展趋势[J].机械设计与制造，2012（4）：279-281.

[7] Adib H， Gilgert J， Pluvinage G.Fatigue life duration prediction for welded spots by volumetric method[J].Int J Fatigue，2004（26）：81-94.

[8] Mohammad A，Taheri A K，Bakhtiarydavijani A.A new analysis method of the dry sliding wear process based on the low cycle fatigue theory and the finite element method[J].Journal of Materials Engineering and Performance，2014，23（3）：1096-1106.

[9] Alush H， Katz Y， Maros M B， et al.Some insights into the remote strain versus fatigue life relationship[J].Journal of Materials Processing Tech，2004（157）：16-22.

[10]张国栋，刘绍伦，何玉怀，等.定向合金DZ125热/机械疲劳寿命预测模型评估[J].航空动力学报，2004，19（1）：17-22.

[11]张国栋，刘绍伦，何玉怀，等.粉末冶金盘材料FGH95热机械疲劳寿命预测[J].失效分析与预防，2008，3（1）：54-58.

[12]周胜田，刘均，黄宝宗.钛合金TC4低周疲劳连续损伤力学研究[J].机械强度，2008，30（5）：798-803.