不同固结状态下黏土抗剪强度与剪切速率的关系
史卜涛,张 云,王哲成,吴吉春,于 军,龚绪龙
(1.南京大学地球科学与工程学院,江苏南京 210046;2.江苏省地质调查研究院,江苏南京 210018)
抗剪强度是边坡稳定分析、地基承载力评价的重要指标。然而不同的剪切速率,岩土材料的抗剪强度不尽相同[1],有时还会相差很大。而且在土工施工过程中,土坝、路堤等施工期的长短,不仅影响到土体固结状态,而且影响土体的强度[2-3]。因此研究不同固结状态下土体剪切速率对抗剪强度的影响,对评价填筑堤坝和地基的稳定性具有重要的意义。
20世纪50年代,Casagrande等[4]研究了加载速率对抗剪强度的影响,此后国内外学者又进行了丰富和系统性的研究。Bro等[5]利用直剪仪研究了超固结比为1~1.5的高岭土在不同剪切速率下抗剪强度的变化,结果表明抗剪强度随着剪切速率的增大而增大。Ajmera等[6]用不同剪切速率对含90% 高岭土和10%石英的混合土试样进行剪切试验,所得试样的内摩擦角随剪切速率的增大而降低。Anim[7]用直剪试验研究了堆石土的抗剪强度指标,发现堆石土的黏聚力和内摩擦角都随剪切速率的增大而增大,而且剪切速率对含水土样内摩擦角的影响比干燥土样更为明显。阚卫明等[8]利用直剪试验研究了宁波粉质黏土的抗剪强度指标随剪切速率的变化情况。与堆石土[7]的试验结果相比,宁波粉质黏土黏聚力也随着剪切速率的增大而增大,但内摩擦角随着剪切速率的增大而减小。在相同的垂直应力作用下,随着剪切速率的增大,抗剪强度逐渐减小,且垂直应力越大,抗剪强度减小的幅度越明显。以上试验采用直剪仪,没有考虑孔隙水压力的影响。文献[9]指出在三轴不排水条件下,剪切速率不仅影响孔隙水压力分布,而且影响有效应力的路径。Crawford[10]对Leda黏土研究发现,在三轴不排水试验中,应当考虑应变速率对孔隙水压力的影响。Kimura等[11]通过三轴不排水试验,发现黏性土在不同应变速率条件下,试样的底部、外围和中间的孔隙水压力变化是不同的。三轴不排水试验测得的孔隙水压力是底部、外围和中间的,由于黏性土渗透性较差,不同剪切速率引起的剪切带周围孔隙水压力的变化与试样周围的孔隙水压力是不同的。此外,文献[12]对黄土研究发现,三轴试验有劈裂、剪切和鼓胀三种破坏模式。而且三轴不排水试验测得的孔隙水压力并不能表征剪切破坏带的孔隙水压力变化,而且以目前的试验设备测量剪切破坏带的孔隙水压力变化是比较困难的。此外,三轴试验在剪破坏模式下剪切带的形状和位置,也是难以确定的。
相对而言,直剪试验剪切破坏面是人为给定的,而且不同剪切速率引起的剪切带附近孔隙水压力的骤变的情况会通过法向应力及破坏剪应力反映出来。因此本文采用直剪仪对超固结比为1,2,3的土样,在剪切速率分别为0.02,0.1,0.5,0.8 和2.4 mm/min 进行直剪试验,研究剪切速率对不同超固结比土样的剪应力-剪切位移曲线及抗剪强度参数的影响。从黏聚力和内摩擦力的角度,分析不同剪切速率条件下土体抗剪强度的主要控制因素。从不同剪切速率引起的孔隙水压力骤变来分析抗剪强度指标变化的原因。
1 试样制备及试验方案
试验土样为射阳地区重塑黏土,其基本参数如表1所示。将土体在自然状态下风干后,粉碎,过0.1 mm的筛,测其风干含水率,用压样法制备干密度为1.537 g/cm3的土样,每个超固结比制备5组土样,每组土样4个,将带环刀的土样装入饱和器,并放入真空缸中,使试样完全饱和。

表1 土样基本参数Table 1 Basic parameters of the soil samples
利用制备好的土样,根据前期固结压力与剪切时的法向应力比值的不同,得到不同超固结比的土样,分别设置超固结比为1,2,3。对每一种超固结比的土样,分别在不同的剪切速率下剪切,研究剪切速率对正常固结土及超固结土抗剪强度及其参数的影响。具体试验步骤如下:
取出带环刀的饱和土样,将土样慢慢压入剪切盒中。根据表2,分别在试样上施加“初始状态”对应的垂直应力,加压5 min后,向剪切盒内加水,24 h后,再将土样上的垂直应力调整到表2对应的“剪切状态”的垂直应力,待稳定后,以0.02 mm/min剪切速率进行剪切。重复以上步骤分别按照0.1,0.5,0.8和2.4 mm/min的剪切速率剪切。
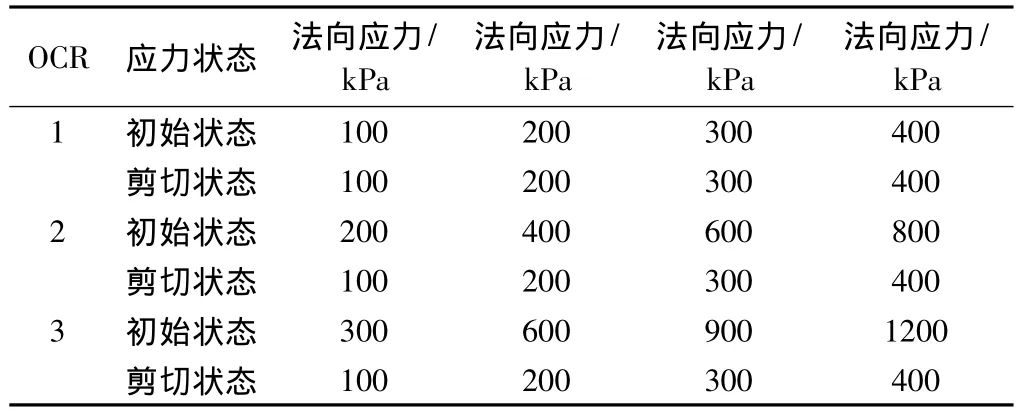
表2 初始与剪切状态加载应力Table 2 Vertical stresses in the initial and shearing states
2 试验结果及分析
2.1 剪应力–剪切位移曲线特性

图1 不同剪切速率下剪应力-剪切位移曲线Fig.1 Shear stress-shear displacement curves under different shear rates
图1为土样在超固结比分别为1,2,3情况下以不同速率剪切时所测的剪应力-剪切位移曲线。在3种固结条件下,剪应力-剪切位移曲线有两种形式:(1)硬化型。在超固结比为1的状态下,剪应力-剪切位移曲线在剪切速率为 0.02,0.1,0.5,0.8 mm/min条件下呈硬化趋势。(2)软化型。超固结(OCR=2、OCR=3)状态条件下,剪应力-剪切位移曲线呈软化趋势,而且超固结比越大,曲线软化趋势越明显。正常固结土在2.4 mm/min条件下也呈软化趋势。软化型曲线有2种形式,一种为达到峰值点即进入软化阶段,如在超固结比为3、法向应力为300 kPa、剪切速率为2.4 mm/min的曲线。另一种为达到峰值点后有一段平缓曲线,然后进入到软化阶段,如超固结比为3、法向应力为400 kPa、剪切速率为2.4 mm/min的曲线。
2.2 抗剪强度与剪切速率的关系

图2 不同超固结条件下峰值剪应力和剪切速率的关系Fig.2 Relationship between the peak shear stress and the shear rate under different OCR
对图1中OCR=1的剪应力-剪切位移曲线没有峰值,根据《土工试验方法标准》,取剪切位移为4 mm对应的剪应力为抗剪强度。在不同固结条件下剪应力-剪切位移曲线上峰值剪应力和剪切速率的关系如图2所示。在相同法向应力条件下,正常固结土的峰值剪应力随着剪切速率的增大而减小,随着法向应力的增加,剪切速率对峰值剪应力的影响越明显。超固结比OCR=2的超固结土,在相同法向应力条件下,峰值剪应力随着剪切速率的增大而呈增大的趋势,但在剪切速率为0.5 mm/min、法向应力为100 kPa和400 kPa的条件下,峰值剪应力偏小。对于超固结比OCR=3的超固结土,在相同法向应力条件下,峰值剪应力随着剪切速率的增大而增大。
本试验在剪切位移为7 mm时停止剪切,虽然在直剪试验中,剪切位移达7 mm时试样的应力状态已经完全偏心,不能表征土体的强度,但是可以作为一个特例,并以此分析剪切速率与破坏后的强度的关系,如图3。

图3 剪切位移为7 mm时剪应力和剪切速率的关系Fig.3 Relationship between the shear stress and the shear rate at the shear displacement of 7 mm
对于超固结比OCR=2的超固结土,在相同法向应力条件下,剪切位移为7 mm对应的剪应力随着剪切速率的增大而增大。对于超固结比OCR=3的超固结土,在相同法向应力条件下,剪切位移为7 mm对应的剪应力随着剪切速率的增大而呈不规则变化的趋势。
2.3 剪切速率与强度参数的关系
根据摩尔-库伦强度破坏理论,绘制不同剪切速率下土体强度破坏曲线,得到剪切速率和内摩擦角、黏聚力的关系。剪切速率大于0.02 mm/min时,要考虑孔隙水压力的影响,得到的内摩擦角和黏聚力是总强度的参数。
(1)剪切速率与内摩擦角的关系
图4中,试样为饱和重塑土,在正常固结条件下,内摩擦角随剪切速率增大而减小,变化范围较大。超固结比OCR=2的试样,随着剪切速率的增大,内摩擦角减小,但减小幅度较正常固结试样小;超固结比OCR=3的试样,随着剪切速率的增大,内摩擦角略有增大,变化幅度相对于OCR=2的试样减小。用对数曲线拟合内摩擦角与剪切速率的关系,有:

图4 剪切速率与内摩擦角的关系Fig.4 Relationship between the angle of internal friction and the shear rate

式中:k1,k2——土体试验参数;
k3——试验参数;
v——剪切速率/(mm·min-1);
v0——单位剪切速率,取 1 mm/min。
(2)剪切速率与黏聚力的关系
图5为不同固结条件下剪切速率与黏聚力的关系。对于重塑饱和黏性土,在正常固结的条件下,黏聚力为零。对于超固结土,黏聚力随着剪切速率的增大而增大。当剪切速率从0.02 mm/min增加到2.4 mm/min时,对于OCR=2的超固结土,黏聚力从0.45 kPa增加到27.2 kPa;对于OCR=3的超固结土,黏聚力从6.15 kPa增加33.25 kPa。

图5 剪切速率与黏聚力的关系Fig.5 Relationship between the cohesion and the shear rate
从图5得出,对于超固结土,黏聚力随着剪切速率的增大而增大,黏聚力与剪切速率的关系为:

式中:k1',k2',k3'——与土体有关的参数。
(3)不同剪切速率下强度参数的主控制作用
重塑黏性土,在正常固结条件下,内摩擦角随剪切速率的增大而减小,峰值剪应力随着剪切速率的增大而减小。由于黏聚力为零,可以认为内摩擦力在不同剪切速率下对土体的强度起主要控制作用,它影响到土体的峰值剪应力,使得土体本身强度随着剪切速率的增大而减小。超固结土,OCR=2时,黏聚力随着剪切速率的增大而增大,内摩擦角随着剪切速率的增大而减小。峰值应力随着剪切速率的增大先增大后减小然后再增大,在整个剪切过程中黏聚力和内摩擦力共同发挥作用,但在法向应力为100 kPa、400 kPa,剪切速率为0.5 mm/min时,峰值应力偏小,说明在剪切速率为0.02~0.5 mm/min时,内摩擦力起主导作用。在0.5~2.4 mm/min时,黏聚力起主导作用。OCR=3时,黏聚力随着剪切速率的增大而增大,内摩擦角随着剪切速率的增大而增大,但变化范围较小。峰值剪应力随着剪切速率的增大而增大,在不同剪切速率条件下,黏聚力对土体强度起主导作用。因此,不同剪切速率下超固结土的峰值强度受内摩擦力和黏聚力的控制,不同固结条件下,内摩擦力和黏聚力的主导作用不同。
3 破坏机理分析
根据太沙基有效应力原理,土体内的剪应力仅由土体骨架承担。因此,土的抗剪强度表示为破坏面上的有效应力函数,摩尔-库伦公式为:

式中:φ'——有效内摩擦角/(°);
c'——有效黏聚力/(kPa);
u——剪切面上的孔隙水压力/(kPa);
σ——法向应力。
土工试验中的慢剪剪切速率为0.02 mm/min,可以认为黏性土完全排水,得到的强度参数接近有效强度参数。本试验采用剪切速率为0.02~2.4 mm/min,得到的强度参数是总应力参数,结合有效应力参数作对比分析。
3.1 正常固结土
如图6,有效强度破坏线为τ=f(σ'),破坏曲线上有一点(σ1,τ1),此点是法向应力为 σ1时,抗剪强度为τ1。当剪切速率变大,在剪切面附近土体骨架应变率增大。由于黏性土渗透性较差,应变率的增大引起剪切带附近的孔隙水压力增大Δu。此时,实际的有效应力为σ2=σ1-Δu,对应有效强度破坏曲线τ=f(σ')上的点为(σ2,τ2),此时土体骨架发生剪切破坏,但是进行拟合破坏线采用的是总应力,即对应的点为(σ1,τ2),对各试验点拟合得到图6中τ=f(σ,v)的破坏线。

图6 不同剪切速率破坏线变化示意图Fig.6 Failure lines at different shear rates
从图6中可以看出,不同剪切速率引起的孔隙水压力骤变的增量与破坏剪应力的减小量成正比,有:

式中:Δτf——相同法向应力σ作用下,不同剪切速率(相差Δv)引起的破坏剪应力变化量;
Δu——不同剪切速率产生的孔隙水压力变化量。
3.2 超固结土
图7中,红色实线表示有效强度破坏线τ=f(σ',c'),蓝色实线表示在剪切速率为v时的破坏线τ=f(σ,c,v)。与正常固结土不同,超固结土的内摩擦角和黏聚力都受剪切速率的影响。同样,不同的剪切速率,在破坏剪切带周围产生了不同的孔隙水压力。根据图7中的关系有:

式中:Δc——相同法向应力σ作用下,不同剪切速率(相差Δv)引起的黏聚力变化量。
从另一方面,根据上述分析及文献[4]~[11]都表明土体的强度是受剪切速率影响的。结合式(2)破坏剪应力、黏聚力和孔隙水压力是剪切速率的函数。在一定的法向应力作用下,对式(3)求导:

对式(6)按照泰勒级数展开并消去高阶项,得到:
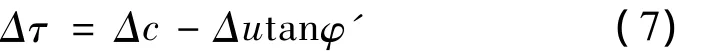

图7 超固结土在不同剪切速率下的破坏线Fig.7 Failure lines of the over-consolidated soils at different shear rates
可以看出式(7)和(5)是一致的,说明利用图7的分析是合理而准确的。对于重塑黏性土,黏聚力变化为零,消去黏聚力项Δc就得到正常固结黏土公式(4)。因此,进一步说明剪切速率对土体强度影响,主要是通过剪切面周围的孔隙水压力骤变来反映的。对于超固结土,不同剪切速率引起的黏聚力变化量减去破坏剪应力变化量的差值与孔隙水压力的增量成正比。
4 结论
(1)正常固结土剪应力-剪切位移曲线在较低剪切速率条件下呈硬化型;在高剪切速率条件下呈软化型。超固结土在不同剪切速率条件下均呈软化型。
(2)正常固结土的抗剪强度随着剪切速率的增大而减小,超固结土的抗剪强度随着剪切速率的增大而增大。在抗剪强度参数方面,对于正常固结土,剪切速率越大,内摩擦角越小。对于超固结土,剪切速率越大,黏聚力越大。
(3)不同剪切速率条件下,内摩擦力和黏聚力对抗剪强度的主导作用不同。正常固结土黏聚力为零,内摩擦力起主导作用。OCR=3时,随着剪切速率的增大,内摩擦力变化幅度较小,而总强度增大。因此,随着剪切速率的增大,黏聚力对土体强度的主导作用在加强。
(4)在相同的法向应力下,对于正常固结土,不同剪切速率引起的剪切带周围孔隙水压力变化量与破坏剪应力变化量成正比关系;对于超固结土,黏聚力变化量减去破坏剪应力变化量的差值与孔隙水压力的增量成正比。
[1] 刘玲霞,李向全,周志超,等.强震条件下谢家店滑坡碎屑流发生机制试验研究[J].水文地质工程地质,2011,38(3):104-109.[LIU L X,LI X Q,ZHOU Z C,et al.An experimental study of the initiation mechanism of landslide debris flow under a strong earthquake[J].Hydrogeology & Engineering Geology,2011,38(3):104-109.(in Chinese)]
[2] 李广信,吕禾.土强度试验的排水条件与强度指标的应用[J].工程勘察,2006(3):11-14.[LI G X,LYU H.Drainage conditions for tests of soil strength and the application of strength indices[J].Journal of Geotechnical Investigation and Surveying,2006(3):11-14.(in Chinese)]
[3] 胡海军,魏丽敏,冷伍明.黏土强度指标的测定和选取[J].岩土力学,2007,28(12):2698-2704.[HU H J,WEI L M,LENG W M.Determination and choice of strengthen index of clay[J].Rock and Soil Mechanics,2007,28(12):2698-2704.(in Chinese)]
[4] Casacrande A,Wilson S D.Effect of rate of loading on the strength of clays and shales at constant water content[J].Geotechnique,1951,2(3):251-263.
[5] Bro A D,Stewart J P,Pradel D E.Estimating undrained strength of clays from direct shear testing at fastdisplacementrates[J]. Geocongress2013 Stability and Performance of Slopes and Emban kments III,2013,231(5).
[6] Ajmera B,Tiwari B,Shrestha D.Effect of Mineral Composition and Shearing Rates on the Undrained Shear Strength of Expansive Clays[C]//GeoCongress 2012@State of the Art and Practice in Geotechnical Engineering,ASCE,2012:1185-1194.
[7] Anim K.Effect of Strain Rate on the Shear Strength of Questa Rock Pile Materials[D].New Mexico Institute of Mining and Technology,2010.
[8] 阚卫明,刘爱民.剪切速率对粉质黏土抗剪强度的影响[J].中国港湾建设,2008(2):23-26.[KAN W M,LIU A M.Influence of shear rate upon shear strength of silty clay[J]. China Harbor Engineering,2008(2):23-26.(in Chinese)]
[9] Zhu J G,Yin J H.Strain-rate-dependent stress-strain behavior of over-consolidated Hong Kong marine clay[J].Canadian Geotechnical Journal,2000,37(6):1272-1282.
[10] Crawford C B.The influence of rate of strain on effective stresses in sensitive clay[J].ASTM Special Technical Publication,1960(254):36-61.
[11] Kimura Tsutomu,Saitoh Kunio.The influence of strain rate on pore pressures in consolidated undrained triaxial testson cohesive soils[J]. Soilsand Foundations,1983,23(1):80-90.
[12] 邢鲜丽,李同录,李萍,等.黄土抗剪强度与含水率的变化规律[J].水文地质工程地质,2014,41(3):53-59.[XING X L,LI T L,LI P,et al.Variation regularities of loess shear strength with the moisture content[J].Hydrogeology & Engineering Geology,2014,41(3):53-59.(in Chinese)]

